
Занятие №14:
Столкновения

Разновидности удара

Центральный удар

Законы сохранения
m_1
m_2
\vec{p}_1 = m_1\cdot\vec{v}_1
m_1
m_2
\vec{v}_1
\vec{v}_2
K_1 = \dfrac{m_1\cdot v_1^2}{2}
\vec{p}_2 = m_2\cdot\vec{v}_2
K_2 = \dfrac{m_2\cdot v_2^2}{2}
\vec{v}'_1
\vec{v}'_2
\vec{p}'_1 = m_1\cdot\vec{v}'_1
K'_1 = \dfrac{m_1\cdot v_1^{'2}}{2}
\vec{p}'_2 = m_2\cdot\vec{v}'_2
K'_2 = \dfrac{m_2\cdot v_2^{'2}}{2}

Алгоритм моделирования
import numpy as np
from numpy import absolute as nabs
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
def collision(x1, vx1, x2, vx2, radius, mass1, mass2):
r12 = np.sqrt((x1-x2)**2) # Расчет расстояния между центрами частиц
# Проверка условия на столкновение: расстояние
# должно быть меньше 2-х радиусов
if r12 <= 2*radius:
# Пересчет скорости первой частицы
VX1 = vx1 * (mass1 - mass2) / (mass1 + mass2)\
+ (2) * mass2 * vx2 / (mass1 + mass2)
# Пересчет скорости второй частицы
VX2 = vx2 * (mass2 - mass1) / (mass1 + mass2)\
+ (2) * mass1 * vx1 / (mass1 + mass2)
else:
# Eсли условие столкновнеия не выполнено,
# то скорости частиц не пересчитываются
VX1, VX2 = vx1, vx2
return VX1, VX2
def move_func(s, t):
x1, v_x1, x2, v_x2 = s
dx1dt = v_x1
dv_x1dt = 0
dx2dt = v_x2
dv_x2dt = 0
return dx1dt, dv_x1dt, dx2dt, dv_x2dt# Парамаетры и условия тестового примера
T = 10
N = 500
mass1 = 1
mass2 = 1
radius = 0.5
x10 = 0
x20 = 5
v10 = 1
v20 = - 1
x1 = [x10]
x2 = [x20]tau = np.linspace(0, T, N)
for k in range(N-1):
t = [tau[k], tau[k+1]]
s0 = x10, v10, x20, v20
sol = odeint(move_func, s0, t)
x10 = sol[1, 0]
x20 = sol[1, 2]
x1.append(x10)
x2.append(x20)
v10 = sol[1, 1]
v20 = sol[1, 3]
res = collision(x10, v10, x20, v20, radius, mass1, mass2)
v10 = res[0]
v20 = res[1]# Строим решение в виде графика и анимируем
fig, ax = plt.subplots()
ball_1, = plt.plot([], [], 'o', color='r', ms=25)
ball_2, = plt.plot([], [], 'o', color='r', ms=25)
def animate(i):
ball_1.set_data((x1[i], 0))
ball_2.set_data((x2[i], 0))
ani = FuncAnimation(fig,
animate,
frames=N,
interval=30)
ax.set_xlim(-5, 10)
ax.set_ylim(-1, 1)
plt.show()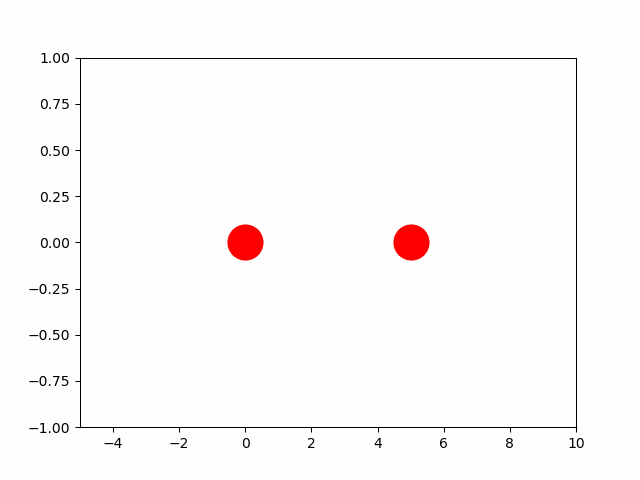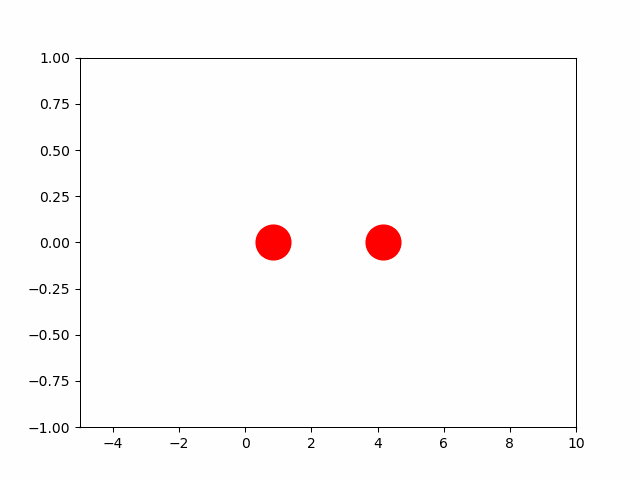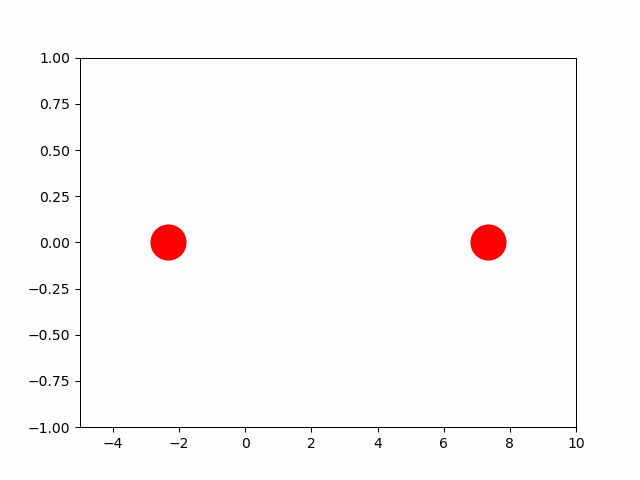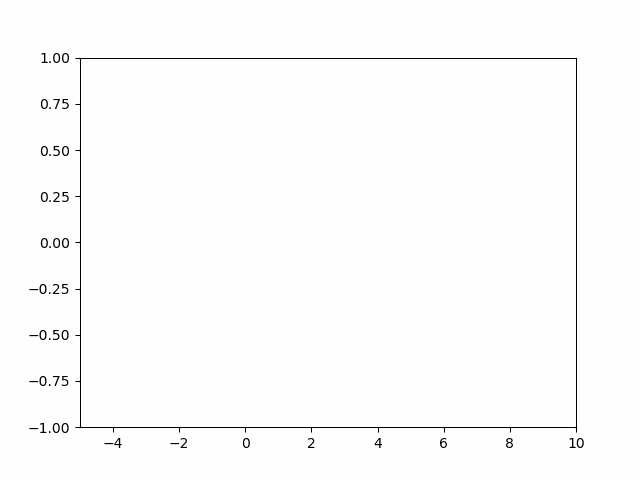

Реальный удар

Коэффициент восстановления
v'_1
Реальный центральный удар
=
v_1
+
\dfrac{(1 + K) \cdot m_2 \cdot (v_2 - v_1)}{m_1 + m_2}
v'_2
=
v_2
+
\dfrac{(1 + K) \cdot m_1 \cdot (v_1 - v_2)}{m_1 + m_2}
K = 0
K = 1
\LARGE \cdot
\LARGE \cdot
- абсолютно неупругий удар
- абсолютно упругий удар
Промежуточные значения соответствуют различной степени неупругости

Нецентральный удар

Законы сохранения
\vec{p}_1
K_1 = \dfrac{m_1\cdot v_1^2}{2}
K_2 = \dfrac{m_2\cdot v_2^2}{2}
\vec{p}'_1 = m_1\cdot\vec{v}'_1
K'_1 = \dfrac{m_1\cdot v_1^{'2}}{2}
\vec{p}'_2 = m_2\cdot\vec{v}'_2
K'_2 = \dfrac{m_2\cdot v_2^{'2}}{2}
+
\vec{p}_2
=
\vec{p}_1
+
\vec{p}_2

Большая формулина

Спасибо за понимание!
Лекция №14. Столкновения
By Alexey Baigashov
Лекция №14. Столкновения
- 152



