Занятие №9:
Дифференциальное уравнение
Постановка дифференциальной задачи
Виды уравнений
линейное уравнение
A \cdot x + B = 0
квадратное уравнение
A \cdot x^2 + B \cdot x + C = 0
A \cdot x^3 + B \cdot x^2 + C \cdot x + D = 0
....
A \cdot \log_{10}(x) + B \cdot \sin(x) + D \cdot e^x + E = 0
....
A \cdot \frac{dy}{dx} + B \cdot y(x) + D \cdot x = 0
кубическое уравнение
трансцендентное уравнение
дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение – уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры.
F\left(x, f(x), \frac{df(x)}{dx}, \frac{d^2f(x)}{dx^2}, ... \right)
Алгоритм постановки
Алгоритма нет, но вы держитесь!
Методика:
• определитель изменяемую функцию "f(x)"
• определить независимую переменную величину "x"
• определить начальные условия
Пример - задача
Из эксперимента известно, что скорость радиоактивного распада пропорциональна количеству вещества. Определить закон изменения количества вещества со временем и найти период, за который распадется половина вещества (период полураспада).
Тут должен быть еще один мем про радиоактивность, но приличных я не нашел, если найдете - высылайте!
Постановка диф. задачи
Дано:
m
Найти:
Начальное условие:
\frac{\Delta m(t)}{\Delta t}
изменяемая величина -
количество вещества
переменная величина -
t
время
закон изменения
m(t)
со временем:
\frac{\Delta m(t)}{\Delta t} - ?
Решение:
m(0) = m_0
\sim
m(t)
m(t)
\frac{\Delta m(t)}{\Delta t}
\sim
m(t)
-
это исходя из условий задачи
минус – означает, что величина уменьшается
Постановка диф. задачи
\frac{\Delta m(t)}{\Delta t}
=
-
k
\cdot
m(t)
\Delta x
=
x_{\text{конечное}}
-
x_{\text{начальное}}
изменение, малое, но конечное
x_{\text{конечное}}
x_{\text{начальное}}
x_{\text{конечное}}
x_{\text{начальное}}
\Delta
\Delta
Постановка диф. задачи
x_{\text{конечное}}
x_{\text{начальное}}
x_{\text{конечное}}
x_{\text{начальное}}
\Delta
бесконечно малое изменение
\Delta
d
d x
=
x_{\text{конечное}}
-
x_{\text{начальное}}
0
В итоге
\frac{\Delta m(t)}{\Delta t}
=
-
k
\cdot
m(t)
средняя скорость изменения
\frac{d m(t)}{d t}
=
-
k
\cdot
m(t)
\Delta
d
Дифференциальное уравнение
мгновенная скорость изменения
Библиотека SciPy
Библиотека scipy
SciPy – библиотека для языка программирования Python с открытым исходным кодом, предназначенная для выполнения научных и инженерных расчётов
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Пределы изменения переменной величины
# В данной задаче переменной величиной является время
t = np.arange(0, 10**6, 100)
# Запись диф. уравнения в виде функции
def radio_function(m, t):
dmdt = - k * m
return dmdt
# Определение начальных условий и параметров
m_0 = 10
k = 1.61*10**(-6) # Постоянная распада для Висмута 210
Алгоритм численного решения
'''
k_Ur_238 = 4.84*10**(-18) # Уран 238
k_Tl_210 = 8.76*10**(-3) # Талий 210
'''
# Решение дифференциального уравнения функцией odeint
solve_Bi = odeint(radio_function, m_0, t)
# Построение решения в виде графика функции
plt.plot(t, solve_Bi[:,0], label='Распад Висмута 210')
plt.xlabel('Период распада, секунды')
plt.ylabel('Функция распада')
plt.title('Радиоактивный распад')
plt.legend()
plt.show()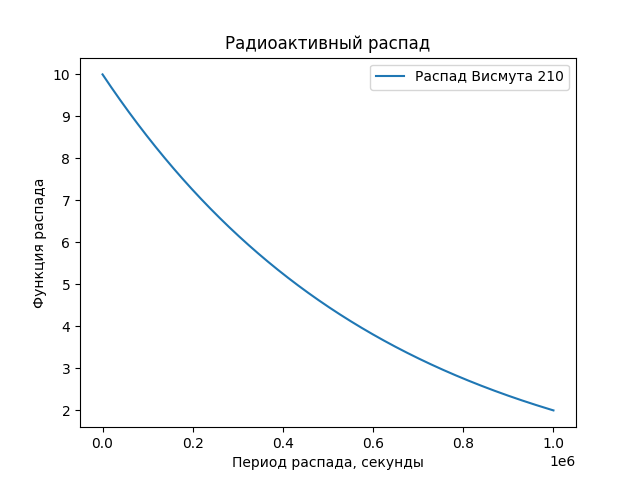
Спасибо за понимание!
Лекция №9. Дифференциальное уравнение
By Alexey Baigashov
