Занятие №10:

Системы дифференциальных уравнений

Решение систем диф. уравнений

\begin{cases} \dfrac{d \theta(t)}{dt} - \omega(t) = 0 \\ \dfrac{d \omega(t)}{dt} + k \cdot \omega + c \sin(\theta(t)) = 0 \end{cases}

Система дифференциальных уравнений

\begin{cases} \dfrac{d \theta(t)}{dt} = \omega(t) \\ \dfrac{d \omega(t)}{dt} = - k \cdot \omega - c \sin(\theta(t)) \end{cases}
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# Определяем переменную величину
t = np.arange(0, 10, 0.01)

# Определяем функцию для системы диф. уравнений
def diff_func(z, t): # z - изменяемая величина для системы
    theta, omega = z # Указание изменяемых функций, через z
	
    # Первое уравнение системы
    dtheta_dt = omega 
    # Второе уравнение системы
    domega_d = - b * omega - c * np.sin(theta) 
    
    return dtheta_dt, domega_d

Алгоритм численного решения

Функция возвращает значения производных системы в том же порядке, в котором они записаны

# Определяем начальные значения и параметры,
# входящие в систему диф. уравнений
theta0 = np.pi - 0.1
omega0 = 0

# Начальное значение изменяемой величины системы
z0 = theta0, omega0

b = 0.25
c = 5.0

# Решаем систему диф. уравнений
sol = odeint(diff_func, z0, t)

# Строим решение в виде графика
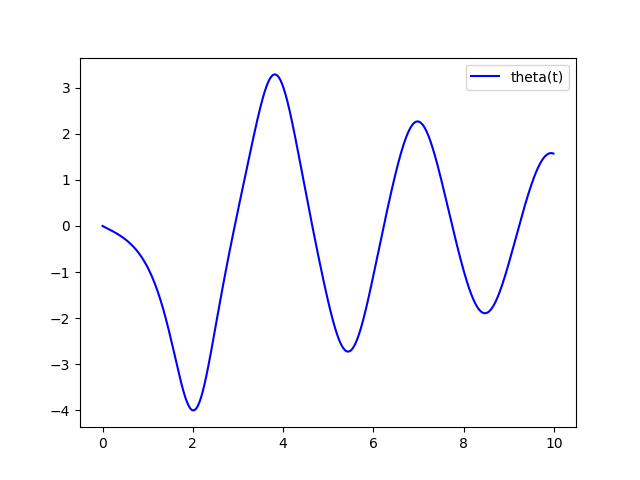
plt.plot(t, sol[:, 1], 'b', label='theta(t)')

plt.legend()
plt.show()

Тут тоже соблюдаем порядок!

# Строим решение в виде графика
plt.plot(sol[:, 1], sol[:, 0], 'g', label='theta(omega)')

plt.legend()
plt.show()
# Строим решение в виде графика
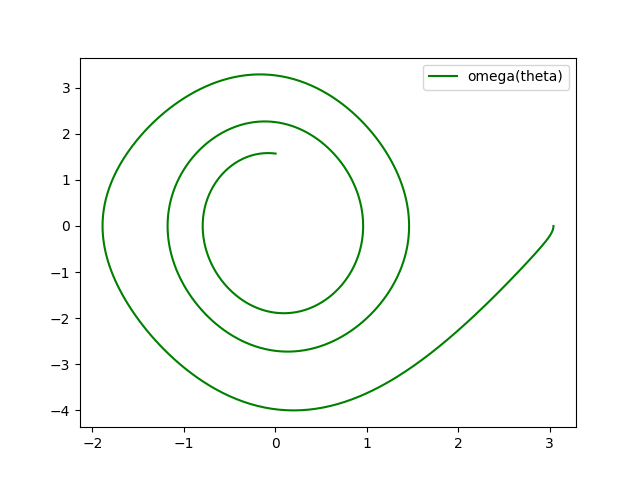
plt.plot(sol[:, 0], sol[:, 1], 'g', label='omega(theta)')

plt.legend()
plt.show()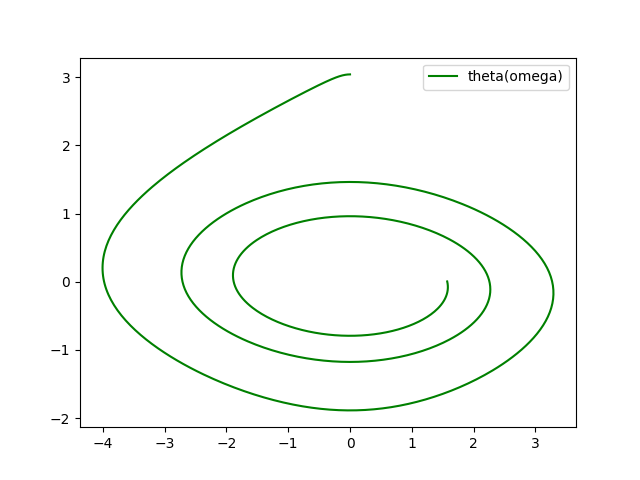

Дифференциальные уравнения второго порядка

y = \dfrac{\Delta x}{\Delta t}
\begin{cases} \dfrac{d x}{d t} = y\\ \\ \dfrac{d y}{d t} = ... \end{cases}

Изменение изменения …

y = \dfrac{d x}{d t}
\dfrac{\Delta y}{\Delta t}
\dfrac{\Delta \left(\dfrac{\Delta x}{\Delta t}\right)}{\Delta t}
\dfrac{\Delta \left(\Delta x\right)}{(\Delta t)^2}
\dfrac{\Delta^2 x}{(\Delta t)^2}
\dfrac{d^2 x}{d t^2}
\dfrac{d^2 x}{d t^2}
\dfrac{d}{d t}
\left(\dfrac{dx}{dt}\right)
\dfrac{d^2 y}{dx^2} - \sin(y) \cdot \dfrac{dy}{dx} + 3xy + 5 = 0
\begin{cases} \dfrac{dy}{dx} = \omega \\ \\ \dfrac{d\omega}{dx} = \sin(y) \cdot \omega - 3xy - 5 \end{cases}

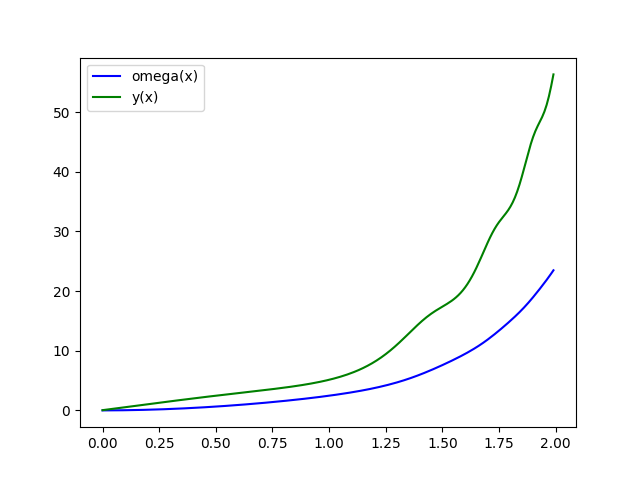
Дифференциальные уравнения второго порядка

# Начальные значения и параметры
y0 = 0.01
omega0 = 0.05
z0 = y0, omega0

Результат

Спасибо за понимание!

Лекция №10. Системы диф. уравнений

By Alexey Baigashov

Made with Slides.com

Лекция №10. Системы диф. уравнений

  • 99

More from Alexey Baigashov