
Занятие №12:
Центральные силовые поля

Постановка задачи

НО в общем виде сила это вектор!
F_G
Одномерная формулировка
=
\dfrac{GMm}{r^2}
F_K
=
\dfrac{kq_1q_2}{r^2}
Одномерные задачи
M, Q
m, q
F_G
F_K
r
O

Двумерная формулировка
F_G
=
\dfrac{GMm}{r^2}
|
\dfrac{\vec{r}}{r}
\cdot
r
=
|\vec{r}|
\vec{F}_G
\vec{F}_G
=
\dfrac{GMm}{r^2} \cdot \dfrac{\vec{r}}{r}
=
\dfrac{GMm}{r^3}\cdot \vec{r}
r
=
\sqrt{x^2 + y^2}
=
\left(x^2 + y^2\right)^{\frac{1}{2}}
\vec{F}_K
=
\dfrac{kq_1q_2}{r^3}\cdot \vec{r}
Аналогично тут и далее

Модель центрального силового поля
\begin{cases}
F_{Gx} = - \dfrac{GMm}{\left(x^2 + y^2\right)^{\frac{3}{2}}}\cdot x \\
\\
F_{Gy} = - \dfrac{GMm}{\left(x^2 + y^2\right)^{\frac{3}{2}}} \cdot y
\end{cases}
Центральное поле
M, Q
\vec{r}
x
x
y
y
M
\ll
m
Q
\ll
q
m, q
\vec{F}_G
=
\{F_{Gx}, F_{Gy}\}

Дифференциальная задача
\vec{F}_G
=
\{ma_{x}, ma_{y}\}
\vec{F}_P
=
m\vec{a}
=
\begin{cases}
m \cdot \dfrac{d^2x}{dt^2} = - \dfrac{GMm}{\left(x^2 + y^2\right)^{\frac{3}{2}}}\cdot x \\
\\
m \cdot \dfrac{d^2y}{dt^2} = - \dfrac{GMm}{\left(x^2 + y^2\right)^{\frac{3}{2}}} \cdot y
\end{cases}
\begin{cases}
a_{x} = \dfrac{d^2x}{dt^2} \\
\\
a_{y} = \dfrac{d^2y}{dt^2}
\end{cases}

\begin{cases}
\dfrac{dx}{dt} = v_x \\
\\
\dfrac{dv_x}{dt} = - \dfrac{GM}{\left(x^2 + y^2\right)^{\frac{3}{2}}} \cdot x
\\
\dfrac{dy}{dt} = v_y \\
\\
\dfrac{dv_y}{dt} = - \dfrac{GM}{\left(x^2 + y^2\right)^{\frac{3}{2}}}\cdot y \\
\end{cases}
Дифференциальная задача

Начальные условия
y
M, Q
x
\vec{v}
\vec{v}
\vec{v}
\vec{v}
x_0
=
149\cdot10^9 \, \text{м}
y_0
=
0 \, \text{м}
v_{x_0}
=
0 \, \text{м/с}
v_{y_0}
=
30 000 \, \text{м/с}
x_0
=
0 \, \text{м}
y_0
=
-149\cdot10^9 \, \text{м}
v_{x_0}
=
30 000 \, \text{м/с}
v_{y_0}
=
0 \, \text{м/с}
x_0
=
-149\cdot10^9 \, \text{м}
y_0
=
0 \, \text{м}
v_{x_0}
=
0 \, \text{м/с}
v_{y_0}
=
-30 000 \, \text{м/с}
x_0
=
0 \, \text{м}
y_0
=
149\cdot10^9 \, \text{м}
v_{x_0}
=
-30000 \, \text{м/с}
v_{y_0}
=
0 \, \text{м/с}
earth
x

Алгоритм решения
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# Определяем переменную величину
frames = 365
seconds_in_year = 365 * 24 * 60 * 60
years = 1
t = np.linspace(0, years*seconds_in_year, frames)
# Определяем функцию для системы диф. уравнений
def move_func(s, t):
x, v_x, y, v_y = s
dxdt = v_x
dv_xdt = - G * m * x / (x**2 + y**2)**1.5
dydt = v_y
dv_ydt = - G * m * y / (x**2 + y**2)**1.5
return dxdt, dv_xdt, dydt, dv_ydt
# Определяем начальные значения и параметры
G = 6.67 * 10**(-11)
m = 1.98 * 10**(30)
x0 = 149 * 10**9
v_x0 = 0
y0 = 0
v_y0 = 30000
s0 = (x0, v_x0, y0, v_y0)# Решаем систему диф. уравнений
def solve_func(i, key):
sol = odeint(move_func, s0, t)
if key == 'point':
x = sol[i, 0]
y = sol[i, 2]
else:
x = sol[:i, 0]
y = sol[:i, 2]
return x, y# Строим решение в виде графика и анимируем
fig, ax = plt.subplots()
ball, = plt.plot([], [], 'o', color='b')
ball_line, = plt.plot([], [], '-', color='b')
plt.plot([0], [0], 'o', color='y', ms=20)
def animate(i):
ball.set_data(solve_func(i, 'point'))
ball_line.set_data(solve_func(i, 'line'))
ani = FuncAnimation(fig,
animate,
frames=frames,
interval=30)plt.axis('equal')
edge = 2*x0
ax.set_xlim(-edge, edge)
ax.set_ylim(-edge, edge)
ani.save('earth_sun.gif')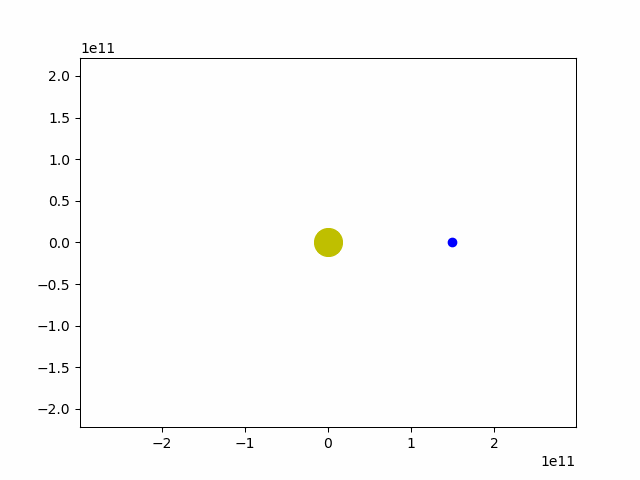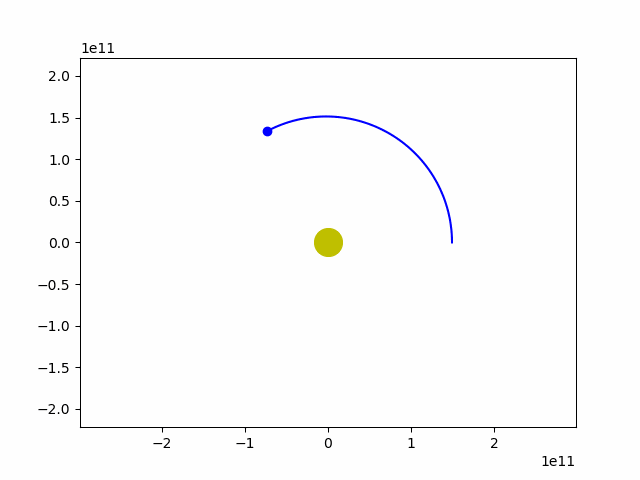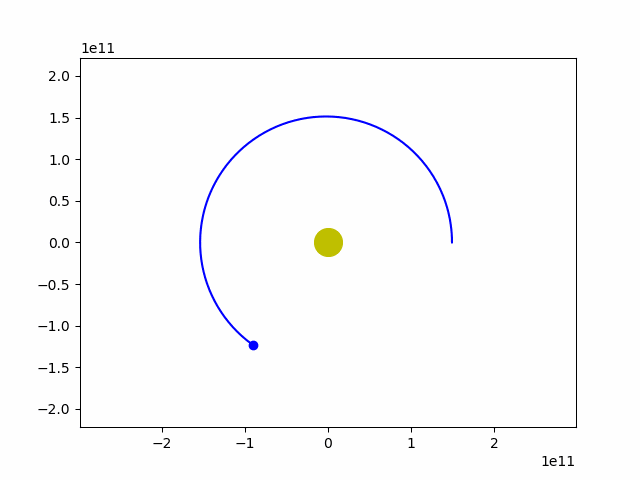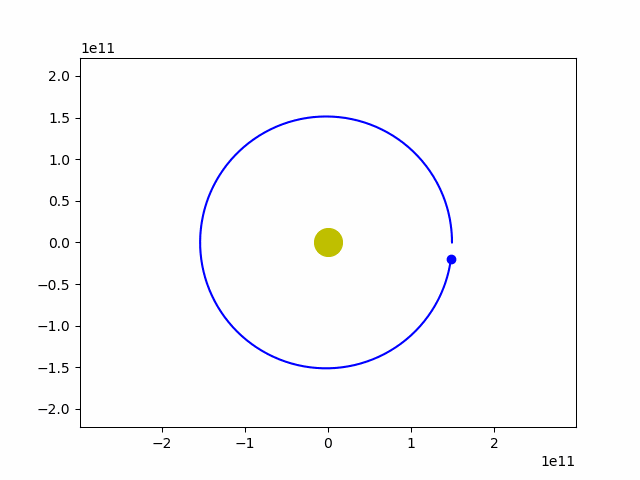

Несколько тел в центральном поле

Начальные условия
y
M, Q
x
\vec{v}
\vec{v}
earth
mercury
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# Определяем переменную величину
frames = 365
seconds_in_year = 365 * 24 * 60 * 60
years = 1
t = np.linspace(0, years*seconds_in_year, frames)# Определяем функцию для системы диф. уравнений
def move_func(s, t):
(x1, v_x1, y1, v_y1,
x2, v_x2, y2, v_y2) = s
dxdt1 = v_x1
dv_xdt1 = - G * m * x1 / (x1**2 + y1**2)**1.5
dydt1 = v_y1
dv_ydt1 = - G * m * y1 / (x1**2 + y1**2)**1.5
dxdt2 = v_x2
dv_xdt2 = - G * m * x2 / (x2**2 + y2**2)**1.5
dydt2 = v_y2
dv_ydt2 = - G * m * y2 / (x2**2 + y2**2)**1.5
return (dxdt1, dv_xdt1, dydt1, dv_ydt1,
dxdt2, dv_xdt2, dydt2, dv_ydt2)# Определяем начальные значения и параметры
G = 6.67 * 10**(-11)
m = 1.98 * 10**(30)
x10 = 149 * 10**9
v_x10 = 0
y10 = 0
v_y10 = 30000
x20 = 0
v_x20 = -47360
y20 = 0.387 * 149 * 10**9
v_y20 = 0
s0 = (x10, v_x10, y10, v_y10,
x20, v_x20, y20, v_y20)# Решаем систему диф. уравнений
def solve_func(i, key):
sol = odeint(move_func, s0, t)
if key == 'point':
x1 = sol[i, 0]
y1 = sol[i, 2]
x2 = sol[i, 4]
y2 = sol[i, 6]
else:
x1 = sol[:i, 0]
y1 = sol[:i, 2]
x2 = sol[:i, 4]
y2 = sol[:i, 6]
return ((x1, y1), (x2, y2))# Строим решение в виде графика и анимируем
fig, ax = plt.subplots()
ball1, = plt.plot([], [], 'o', color='b')
ball_line1, = plt.plot([], [], '-', color='b')
ball2, = plt.plot([], [], 'o', color='r')
ball_line2, = plt.plot([], [], '-', color='r')
plt.plot([0], [0], 'o', color='y', ms=20)
def animate(i):
ball1.set_data(solve_func(i, 'point')[0])
ball_line1.set_data(solve_func(i, 'line')[0])
ball2.set_data(solve_func(i, 'point')[1])
ball_line2.set_data(solve_func(i, 'line')[1])ani = FuncAnimation(fig,
animate,
frames=frames,
interval=30)
plt.axis('equal')
edge = 2*x10
ax.set_xlim(-edge, edge)
ax.set_ylim(-edge, edge)
plt.show()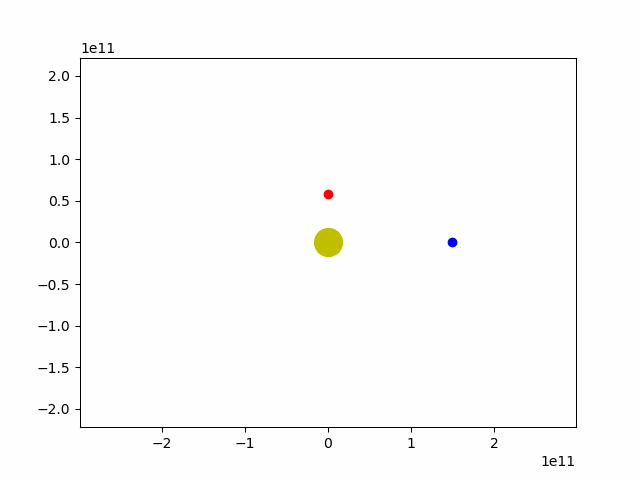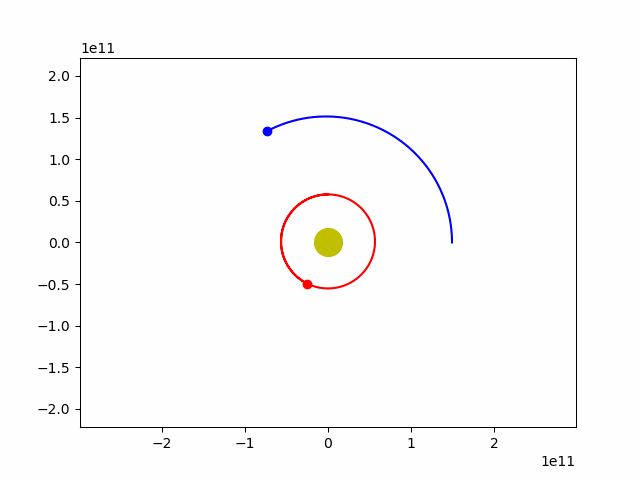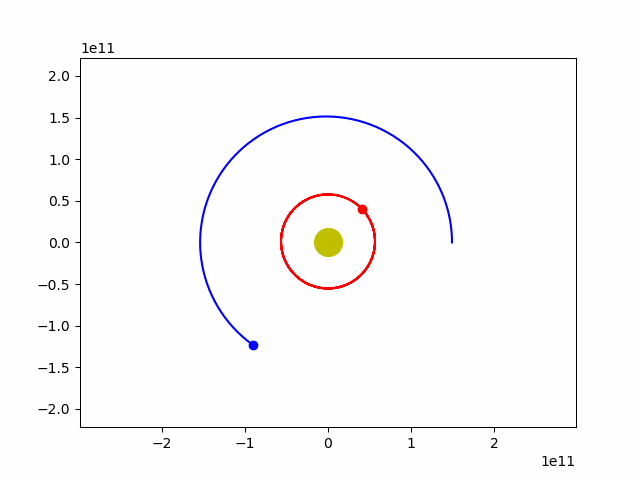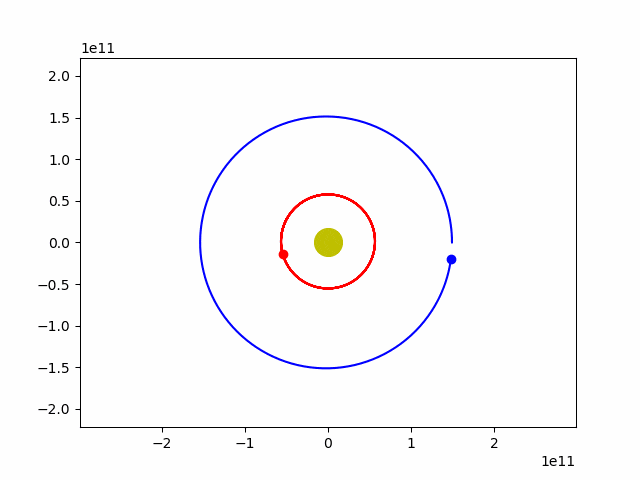

Спасибо за понимание!
Лекция №12. Центральные силовые поля
By Alexey Baigashov
Лекция №12. Центральные силовые поля
- 166



