Занятие №17:
Введение в астрофизику
Природа света
\varepsilon = \hbar \nu
Свет
Частица
Волна
(\lambda, \nu)
(\varepsilon, p)
\varepsilon = \dfrac{\hbar c}{\lambda}
Закон Планка
\nu = \dfrac{c}{\lambda}
Постоянная Планка
\hbar = 6,62 \cdot 10^{-34} \, \text{c} \cdot \text{Дж}
Корпускулярно – волновой дуализм
Видимый свет
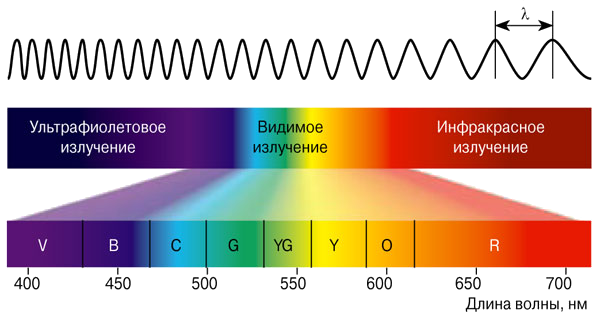
Электро-магнитные волны
Фотометрические величины
Энергетические величины
\varepsilon_1
\varepsilon_2
\varepsilon_3
\varepsilon_n
...
Q = \sum_{i} \varepsilon_i
=
\varepsilon_1
+
\varepsilon_2
+
...
+
\varepsilon_n
\Phi = \dfrac{\Delta Q}{\Delta t}
Опр.: Световой поток
\Delta \Phi
\Delta S
E = \dfrac{\Delta \Phi}{\Delta S}
Опр.: Освещенность
Опр.: Энергия светового пучка
Энергетические величины
Q = [\text{Дж}]
\Phi = \left[ \dfrac{\text{Дж}}{\text{с}} \right] = [Вт]
E = \left[ \dfrac{\text{Вт}}{\text{м}^2} \right]
Зрачок
Хрусталик
Сетчатка
Стекловидное тело
Световые величины
V
Дневное зрение
Опр.: Относительная спектральная световая эффективность монохроматического излучения
Ночное зрение
Преобразование величин
Q_v
=
683
\cdot
Q(\lambda)
\cdot
V
[Q_V] = [\text{лм} \cdot \text{с}]
\Phi_v
=
683
\cdot
\Phi(\lambda)
\cdot
V
[\Phi_V] = [\text{лм}]
E_v
=
683
\cdot
E(\lambda)
\cdot
V
[E_V] = [\text{лк}]
X_v
=
683
\cdot
X(\lambda)
\cdot
V
Люмен
Люкс
Задача №1
Определить сколько люмен приходится на мощность световой энергии в 1 ватт для длин волн в 550 и 450 нм?
Решение
Дано:
\lambda_1 = 550 \, \text{нм};
V_{\text{д}}(\lambda_1) = 1
Найти:
Решение:
\lambda_2 = 450 \, \text{нм};
\Phi_v(\lambda_1) - ?
\Phi_v(\lambda_2) - ?
V_{\text{д}}(\lambda_2) \approx 0.05
V_{\text{н}}(\lambda_2) \approx 0.4
V_{\text{н}}(\lambda_1) \approx 0.5
\Phi = 1 \, \text{Вт}
\lambda_1 = 550 \, \text{нм};
Решение
\Phi_{\text{д}v}(\lambda_1)
=
683
\cdot
1
\cdot
1
лм
=
683
\Phi_{\text{д}v}(\lambda_2)
=
683
\cdot
1
\cdot
0.05
лм
\approx
35
\Phi_{\text{н}v}(\lambda_1)
=
683
\cdot
1
\cdot
0.5
лм
342
\Phi_{\text{н}v}(\lambda_2)
=
683
\cdot
1
\cdot
0.4
лм
273
\approx
\approx
Спасибо за понимание!
Занятие 17. Введение в астрофизику
By Alexey Baigashov
