
Занятие №21:
Введение в астрофизику звезд

Жизнь звезд

Строение вещества




T\downarrow
T\downarrow
T\uparrow
T\uparrow
T\uparrow

Формирование звезд


Газо-пылевое облако
Остывание и сжатие
Формирование идеальной сферы
T\uparrow
=>
P\uparrow
T\uparrow\uparrow
=>
P\uparrow\uparrow
Термоядерные реакции

Жизнь звезд









F_G
F_L
Сила лучистого давления
F_G
F_L
=
Звезда живет!

\varepsilon
Свет, излучённый с поверхности звезды
T\downarrow
Ядро звезды
H_1^1
H_1^1
+
He_4^2
\rightarrow

\varepsilon
T_\text{ядра}
\sim
10^6 \, \text{K}
T_\text{eff}
\sim
10^3 \, \text{K}

Спектральные классы
Класс "О"


T_\text{eff} \in (60 000 \, \text{K}, 30 000 \, \text{K})
\text{Цвет}: \, \text{голубой}
\text{Масса}: \, \sim 60\cdot M_{Sun}
\text{Радиус}: \, \sim 15 \cdot R_{Sun}
\text{Радиус}: \, \sim 15 \cdot R_{Sun}
Класс "B"

T_\text{eff} \in (30 000 \, \text{K}, 10 000 \, \text{K})
\text{Цвет}: \, \text{бело-голубой}
\text{Масса}: \, \sim 18\cdot M_{Sun}
\text{Радиус}: \, \sim 7.5 \cdot R_{Sun}

Класс "A "

T_\text{eff} \in (10 000 \, \text{K}, 7500 \, \text{K})
\text{Цвет}: \, \text{белый}
\text{Масса}: \, \sim 3.1\cdot M_{Sun}
\text{Радиус}: \, \sim 2.1 \cdot R_{Sun}

Класс "F "

T_\text{eff} \in (7500 \, \text{K}, 6000 \, \text{K})
\text{Цвет}: \, \text{бело-желтый}
\text{Масса}: \, \sim 1.7\cdot M_{Sun}
\text{Радиус}: \, \sim 1.3 \cdot R_{Sun}

Класс "G "

T_\text{eff} \in (6000 \, \text{K}, 5200 \, \text{K})
\text{Цвет}: \, \text{желтый}
\text{Масса}: \, \sim 1.1\cdot M_{Sun}
\text{Радиус}: \, \sim 1.1 \cdot R_{Sun}

Класс "K "

T_\text{eff} \in (5200 \, \text{K}, 3700 \, \text{K})
\text{Цвет}: \, \text{оранжевый}
\text{Масса}: \, \sim 0.8\cdot M_{Sun}
\text{Радиус}: \, \sim 0.9 \cdot R_{Sun}

Класс "M "

T_\text{eff} \in (3700 \, \text{K}, 2400 \, \text{K})
\text{Цвет}: \, \text{красный}
\text{Масса}: \, \sim 0.3\cdot M_{Sun}
\text{Радиус}: \, \sim 0.4 \cdot R_{Sun}

Все вместе





Абсолютно черное тело

Определение
Абсолютно чёрное тело – физическое тело, которое при любой температуре поглощает всё падающее на него электромагнитное излучение во всех диапазонах



Закон Стефана-Больцмана

L = 4 \pi R^2 \sigma T_\text{eff}^4

Самые распространенные черные тела в космосе
Звезды
Светимость
\sigma = 5.57 \cdot 10^{-8} \dfrac{\text{Вт}}{\text{м}^2\text{K}^4}
[L] = [\text{Вт}]










Закон Вина
длина волны, на которую приходится максимум интенсивности излучения
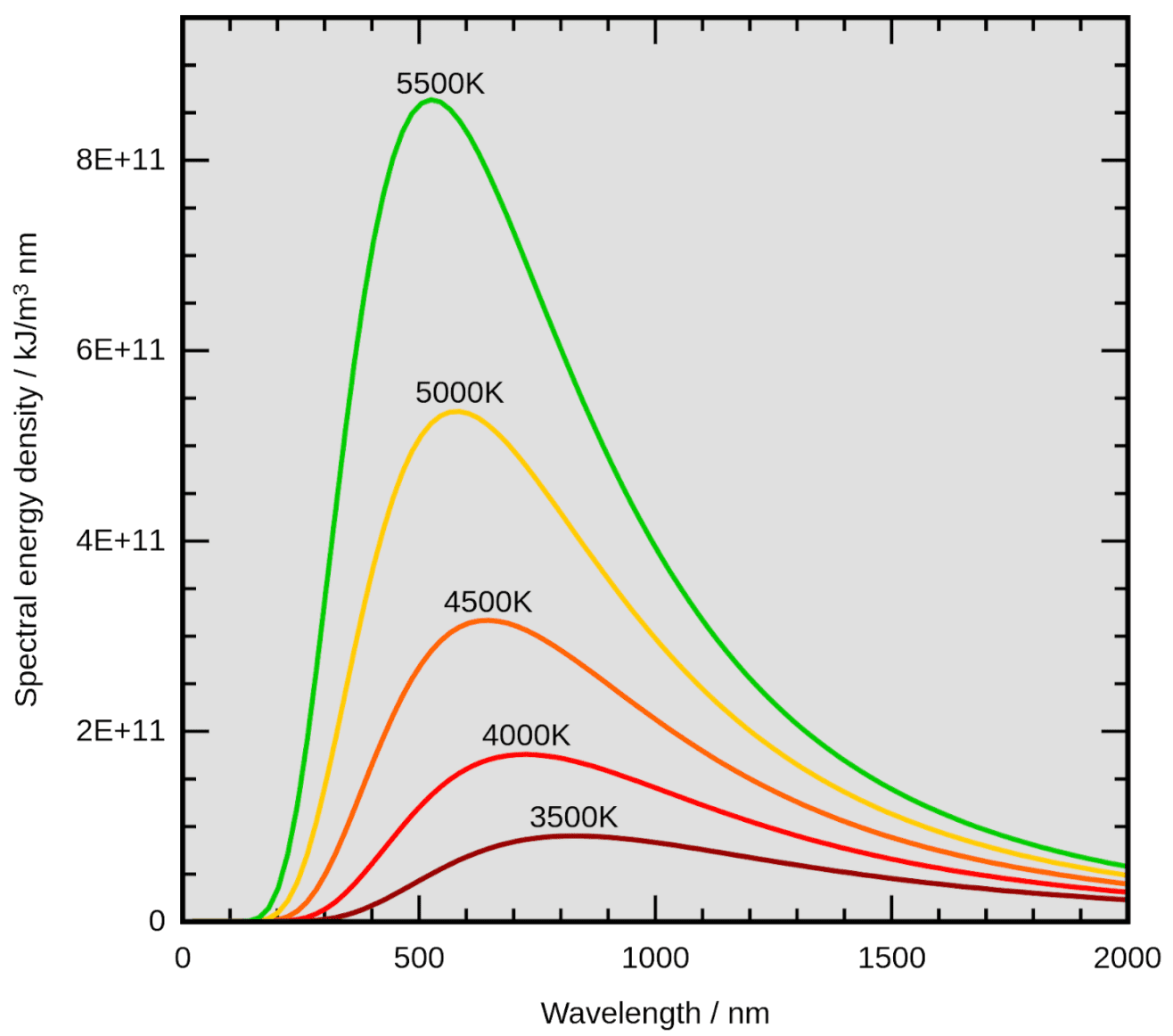
\lambda_{\text{max}}
=
\dfrac{b}{T_{\text{eff}}}
b = 2.897\cdot10^{-3} \, \text{м} \cdot \text{K}

Задача
Определите длину волны, на которую приходится максимум интенсивности излучения Солнца.


Решение
Дано:
Найти:
Решение:
\lambda_{\text{max}}
=
\dfrac{b}{T_{\text{eff}}}
T_{\text{eff}}=5800 \, \text{K}
\lambda_{max}-?
=
\dfrac{2.897\cdot10^{-3}}{5800}
\approx
500 \, \text{нм}


Спасибо за понимание!
Занятие 21. Введение в астрофизику звезд
By Alexey Baigashov
Занятие 21. Введение в астрофизику звезд
- 533



