Neural Network Models in Cell's Image Classification
Our Task
- Build a classifier that identifies images into 9 types
- Get a promising result for future work




Microglia
Neoplastic Astrocyte
Neoplastic Oligodendrocyte
Normal Neuron

Reactive Endothelial
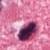
Mitotic Figure
Our Dataset
- Over 2500 expert annotated images with size 50x50
- Divided into 3 sets:
- Train our model based on the training/validation set
- Then evaluate our model on the testing set
1800 images in the training set
360 images in the validation set
360 images in the testing set
Training & Optimization
Mostly Using a Python Library - Theano
Cost Function
Negative Log Likelihood
- if correctly classified, no cost
- if wrong, penalize hard
How to find the cost for classification?
Machine learning is about optimization
Gradient Descent
while True:
loss = f(params)
d_loss_wrt_params = ... # compute gradient
params -= learning_rate * d_loss_wrt_params
if <stopping condition is met>:
return params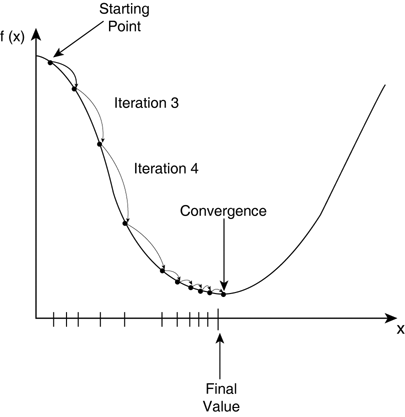
Early-Stopping
A way to combat overfitting
Monitor the model’s performance on a validation set
If the model’s performance ceases to improve sufficiently on the validation set
We stop training earlier without running through the whole process again
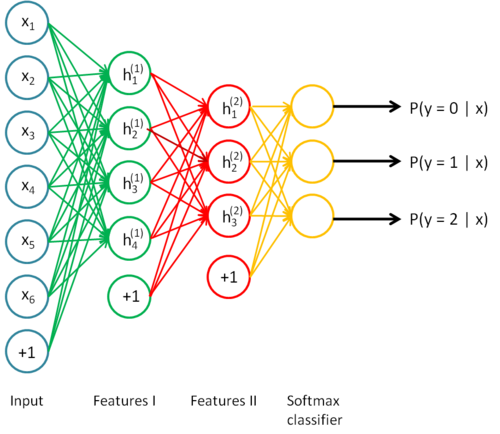
Simple Neural Network Model

Input Layer
Each pixel in the image will be a feature (0 ~ 255)
Each image has three channels (R,G,B)
Each channel has 50*50 pixels
Total feature vector size = 50*50*3 = 7500
Hidden Layer
#of layers and # of neurons in each layer are hyperparameters
Need activate function to learn non-linear boundries
Activate Function
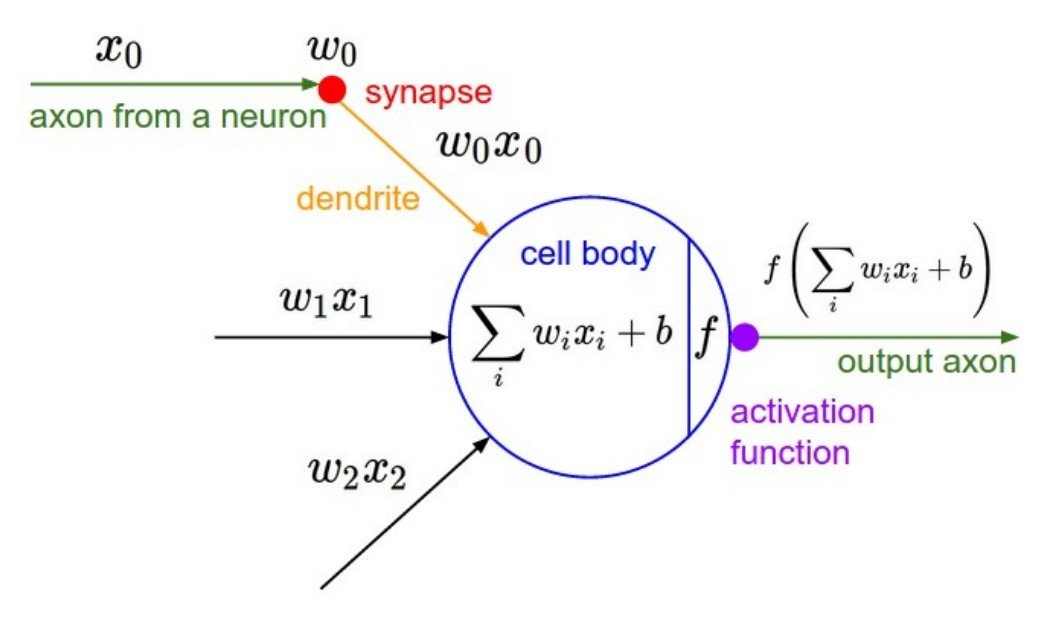
Choices for f : Sigmoid, Tanh,
Rectified Linear Unit (f(x) = max(0,x)) ...
Output Layer
Basically a logistic regression for multiple classes
Inputs are the hidden neurons of previous layers
Cost function is based on the output layer
Output 9 probabilities corresponding to 9 classes
Use back-propagation to calculate gradient and then update weights
Convolutional Neural Networks
First introduced by Yann LeCun to classify hand-written digits (similar to our task)
Works extremely well on image classification when the network is deep
Convolution
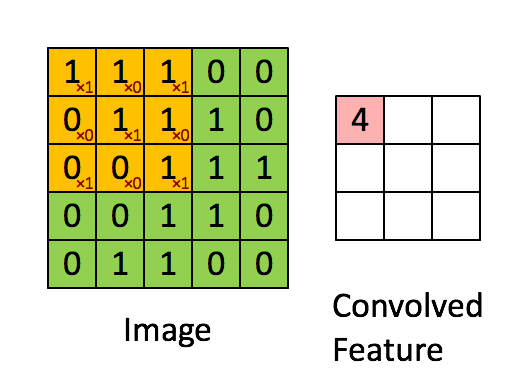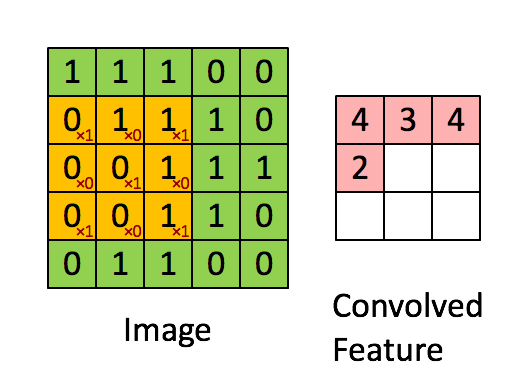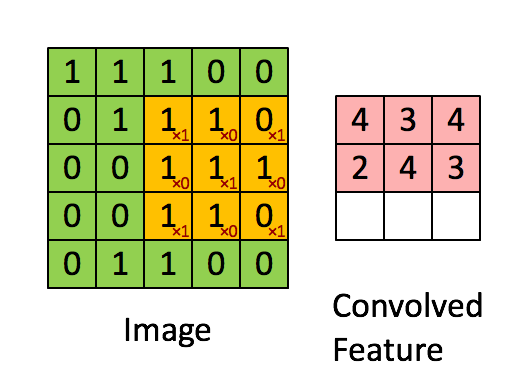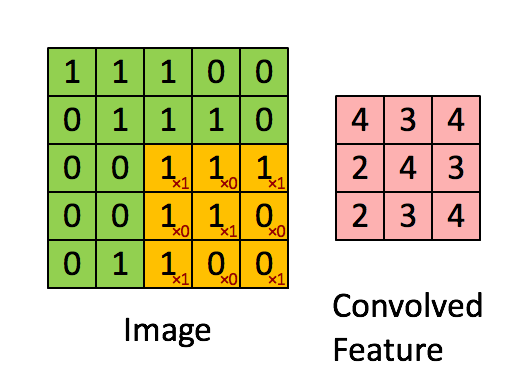
Can be viewed as a feature extractor
inputs: 5x5 image and 3x3 filter
outputs: (5-3+1)x(5-3+1) = a 3x3 feature map
CovNet Example
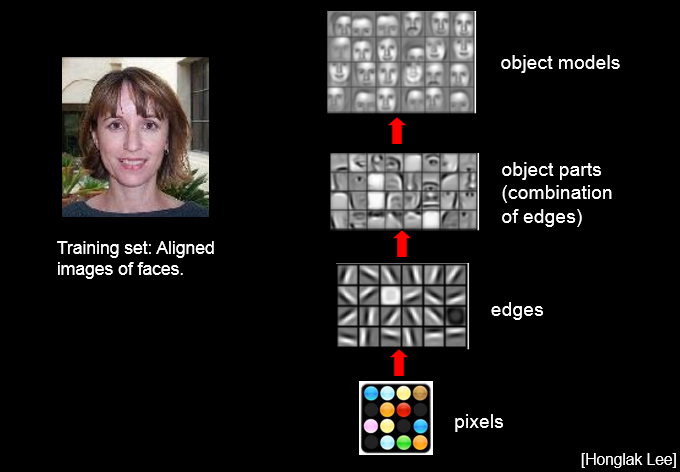
Convolution
inputs: 3x50x50 image and k filters with size 5x5
outputs = ???
We will have 3*(50 - 5 + 1)^2*k many features
Need pooling to reduce the # of features
6,348*k
if k = 25, convolution generates around 160,000 features!
Max-Pooling
Also known as Sub-Sampling
For 2 x 2 pooling, suppose input = 4 x 4
Output = 2 x 2

Architecture
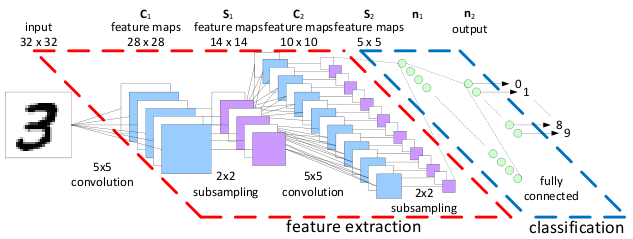
2 convolution layers with pooling
1 hidden layer
1 output layer (logistic regression)
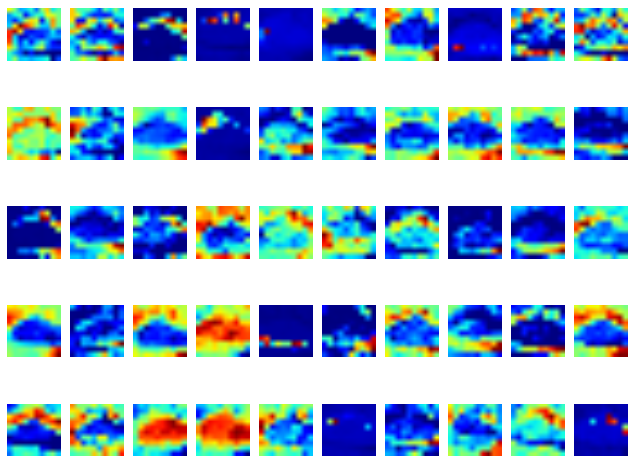
Visualize CNN
Input
First Covolution Layer with 25 filters
Second Covolution Layer with 50 filters
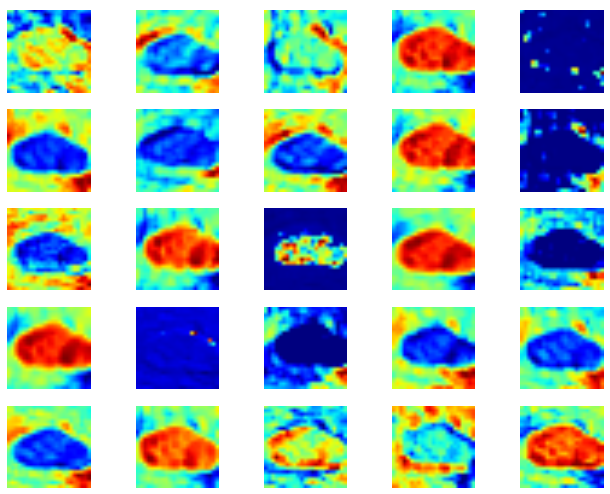
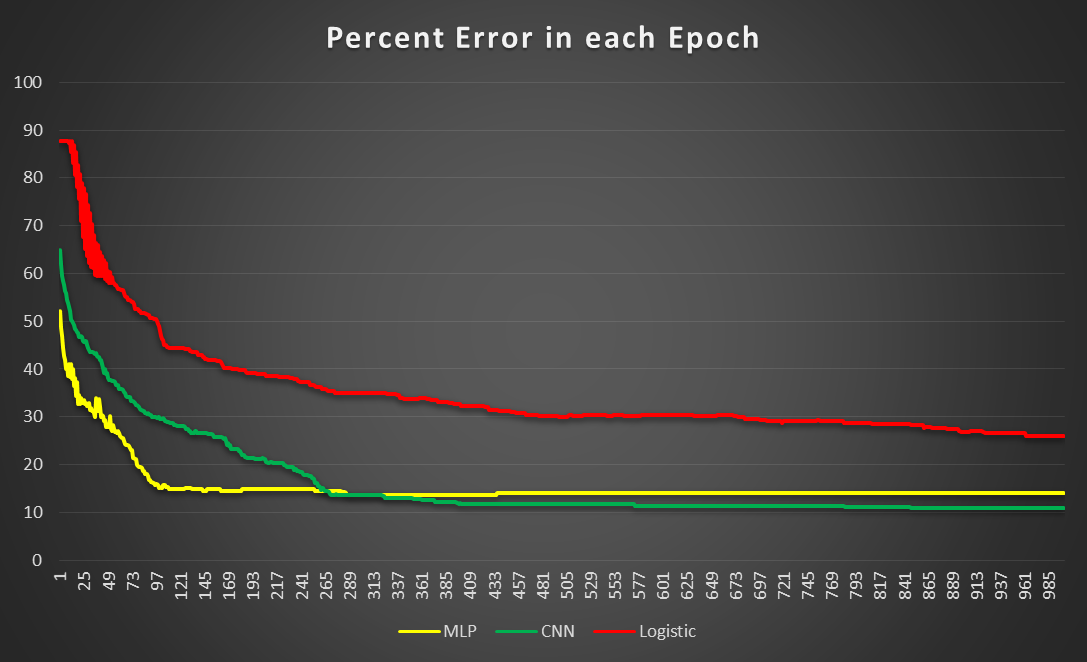
Result for Supervised
- Logistic Regression (Linear Model)
Optimization complete with best validation score of 26.027397 %,with test performance 26.902174 %
- Multi-layer Perceptron (One Hidden Layer)
Best validation score of 13.698630 % obtained at iteration 8610, with test performance 13.858696 %
- Convolutional Neural Network
Best validation score of 10.833333 % obtained at iteration 25440, with test performance 9.166667 %
Comparison Between Models
Unsupervised Learning
Labeled data are limited and expensive
Need medical experts to annotate
Unlabeled data are cheap!
Training on small sample of labeled data may be biased
Why?
Autoencoder
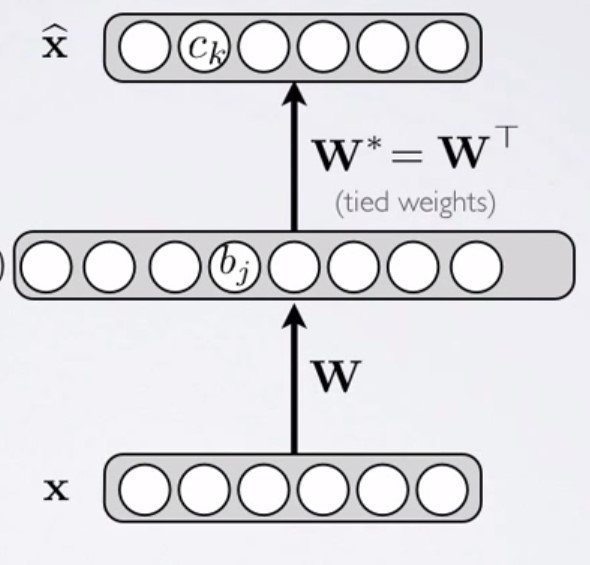
For each input x,
- Do a feed-forward pass to obtain an output x̂
- x̂ is a reconstruction the input x
- Cost is the deviation from x to x̂
- Hidden layer will extract features to reconstruct x
Same idea as neural network but different output
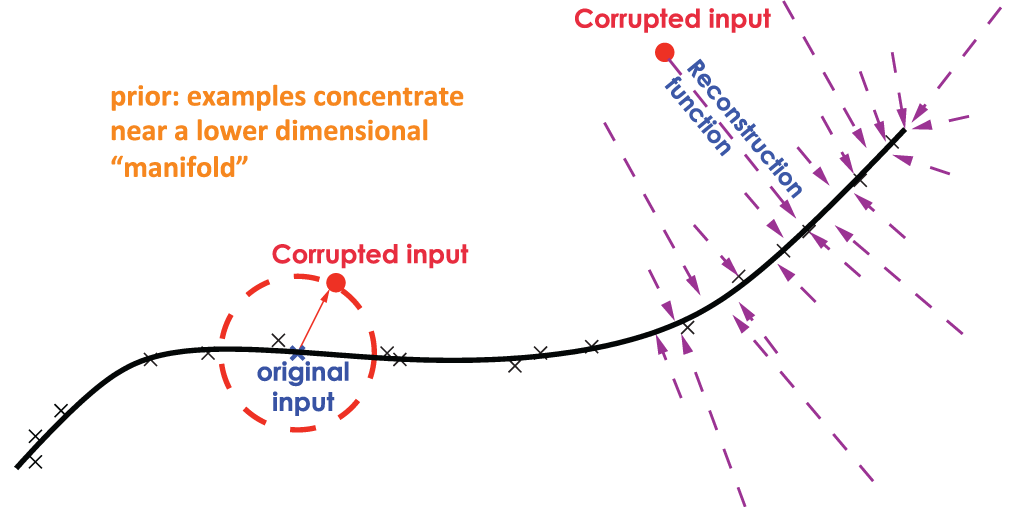
Denoising Autoencoder
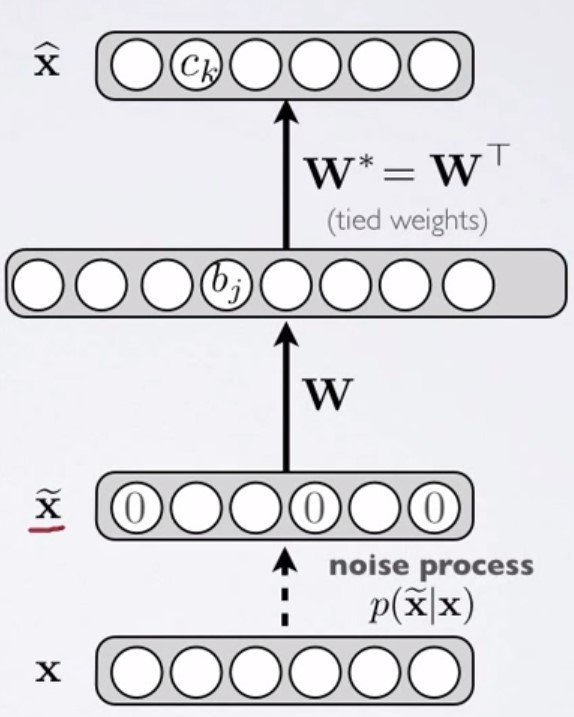
- Pass the corrupted input to our network
- Corrupt: set some of input to be zero by binomial distribution
- Forced the hidden layer to learn robust features
Denoising Autoencoder
trying to predict the corrupted (i.e. missing) values
from the uncorrupted (i.e., non-missing) values


Reconstruction



Raw input
no corruption
40% corruption
Next Steps
-
Unsupervised Pre-training
-
Adjust hyper-parameters
Hyper-Parameters
- Learning Rate
- Number of Layers
- Number of Neurons
- Number of Filters
Semi-Supervised
- Unsupervised Pre-training
- Supervised Fine-tuning
- Use large amount of unlabeled data
- Work as initialization process of weight
Adjust the weight by cost of classification and back-propagation
Questions?
References
- http://ufldl.stanford.edu/
- http://deeplearning.net/tutorial/
- http://cs231n.github.io/
- http://info.usherbrooke.ca/hlarochelle/neural_networks/content.html
- http://en.wikipedia.org/wiki/Autoencoder
Copy of deck
By Abhishek Kumar Tiwari
Copy of deck
- 1,295



