Ako sa dostať do vesmíru

Jakub Havelka    Adam Dej

Časť 1: Orbita

Čo je to orbita?

  • Každá dráha zakrivená graviáciou
  • Newton dokázal že sú to kuželosečky

Ako opísať orbitu?

  • Výstrednosť dráhy (Eccentricity)
  • Veľká polos (Semimajor axis)
  • Uhol sklonu (Inclination)
  • Dĺžka výstupného uzla (Longitude of the ascending node)
  • Argument periapsy (Argument of periapsis)
  • Stredná anomália (Mean anomaly at epoch)

Orbitálna rýchlosť v danom bode

Pre skoro kruhové orbity

v_0 \approx \frac{2 \pi a}{T}
v0≈2πaTv_0 \approx \frac{2 \pi a}{T}

Pre excentrické orbity

v = \sqrt{GM_{zem}\left( \frac{2}{r} - \frac{1}{a}\right)}
v=GMzem(2r−1a)v = \sqrt{GM_{zem}\left( \frac{2}{r} - \frac{1}{a}\right)}

Geosynchrónna orbita

  • Pozorovateľ na zemi vidí satelit vo fixnom bode na oblohe
v_{gs} = 3.1 \frac{km}{s}
vgs=3.1kmsv_{gs} = 3.1 \frac{km}{s}

Vzdialenosti stredov: ~42 000 km

Časť 2: Ako fungujú rakety?

Raketové motory

  • Reakčné motory - tretí Newtonov zákon
  • Čím rýchlejší výfuk tým lepšie
    • ISP - špecifický impulz
  • Tekuté palivo
  • Tuhé palivo
  • Hybridné
  • Termálne
  • Monopropellant

Delta-v

  • Motor pôsobí na raketu nejakou silou
a = \frac{F}{m}
a=Fma = \frac{F}{m}
  • Hmotnosť rakety klesá, míňame palivo
     
  • Zaujímavá informácia: zmena rýchlosti
    • Ktorú sme schopní dosiahnuť s palivom ktoré máme
\Delta v = \int_{t_0}^{t} \frac{F} {m_t} dt
Δv=∫t0tFmtdt\Delta v = \int_{t_0}^{t} \frac{F} {m_t} dt

Tsiolkovského rovnica

\Delta v = v_e ~ ln\frac{m_0}{m_1}
Δv=ve lnm0m1\Delta v = v_e ~ ln\frac{m_0}{m_1}
v_e = g_0 ~ I_{sp}
ve=g0 Ispv_e = g_0 ~ I_{sp}
\Delta v = v_e ln \frac{100}{100 - 80} \approx 1.61 v_e
Δv=veln100100−80≈1.61ve\Delta v = v_e ln \frac{100}{100 - 80} \approx 1.61 v_e
\Delta v = 3 \cdot v_e ln \frac{100}{100 - 80} \approx 4.83 v_e
Δv=3⋅veln100100−80≈4.83ve\Delta v = 3 \cdot v_e ln \frac{100}{100 - 80} \approx 4.83 v_e
\Delta v = v_e ln \frac{100}{100 - 11.2} \approx 2.19 v_e
Δv=veln100100−11.2≈2.19ve\Delta v = v_e ln \frac{100}{100 - 11.2} \approx 2.19 v_e

Staging

Časť 3: Ako meniť orbitu?

Menenie Ap / Pe

Z druheho Keplerovho zákona

r v ~ sin\gamma = \omega r ^2 = \mathrm{const}
rv sinγ=ωr2=constr v ~ sin\gamma = \omega r ^2 = \mathrm{const}

Teda pre periapsu a apoapsu:

r_p v_p = r_av_a
rpvp=ravar_p v_p = r_av_a

Menenie Ap / Pe

Kinetická a potenciálna energia

E_k = \frac{mv^2}{2}
Ek=mv22E_k = \frac{mv^2}{2}
E_p = - \frac{GM m}{r}
Ep=−GMmrE_p = - \frac{GM m}{r}

Zákon zachovania energie

\frac{mv_1^2}{2} - \frac{GMm}{r_1} = \frac{mv_2^2}{2} - \frac{GMm}{r_2}
mv122−GMmr1=mv222−GMmr2\frac{mv_1^2}{2} - \frac{GMm}{r_1} = \frac{mv_2^2}{2} - \frac{GMm}{r_2}

Menenie Ap / Pe

Celkovo dostávame

r_a = \frac{r_p}{\left( \frac{2GM}{r_pv_p^2}\right) - 1}
ra=rp(2GMrpvp2)−1r_a = \frac{r_p}{\left( \frac{2GM}{r_pv_p^2}\right) - 1}

Menenie orbitálnej inklinácie

Rendezvouz

Časť 4: We choose to go to the Minmus

Hohmann transfer

Free-return trajectory

Časť 5: Liftoff, touchdown

Suicide burn

  • Vznášanie plytvá palivo

 

  • Raketa vykonáva spomalený pohyb
  • Brzdnú dráhu vieme zrátať
    • Nezabudnime, že rakete sa mení hmotnosť

Presné pristátie

  • Periapsa nad cieľom
  • Zastavíte nad ním
    • Pozor na terén
  • Jemné korekcie

Vzlet k priamemu stretnutiu

  • Efektívny vzletový profil na orbitu
    • Vieme zrátať, koľko nám to bude trvať
  • Chceme, aby stanica skončila tam kde my

Let atmosférou

  • Odpor vzduchu vs gravitácia
  • Horizontal vs vertical
  • Uhol vletu do atmosféry
    • Plytký: nezabrzdíte
    • Strmý: BURN!

Let atmosférou

Časť 6: These are the voyages of SS Lazyness

Oberthov efekt

Aerobraking

Otázky?

Jakub Havelka    Adam Dej

Ďakujeme za pozornosť

Ako sa dostať do vesmíru (SK)

By Adam Dej

Made with Slides.com

Ako sa dostať do vesmíru (SK)

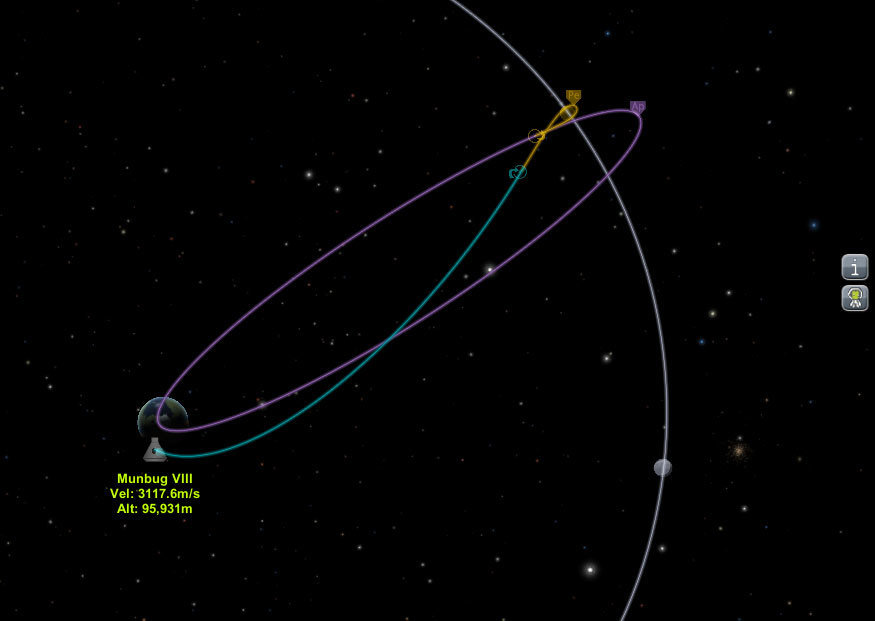
Hrávate Kerbal Space Program? Chcete vedieť, ako ušetriť palivo? Chcete vedieť ako využit gravitačný prak alebo čo je Oberthov efekt? Ako efektívne využívať triky orbitálnej mechaniky? Prídte na túto prednášku! Fyzikálne si vysvetlíme základy orbitálnej mechaniky v Kerbal Space Programe príjemným a doslova hravým spôsobom. Okrem toho si aj ukážeme užitočné triky ako počítať kedy odštartovať z planéty aby sme sa rýchlo stretli s vermírnou stanicou a iné veci.

  • 337

More from Adam Dej