Bence Bakó, Adam Glos, Özlem Salehi, Zoltán Zimborás
Optimal QAOA design for the Traveling Salesman Problem


Quantum Approximate Optimization Algorithm
- A mixture of quantum annealing and VQE
- For gate-based model and combinatorial optimization
- encodes the problem into the circuit
$$|p,r\rangle = \prod_{i=1}^k \exp(-\mathrm{i} p_iH_{\rm mix})\exp(-\mathrm{i} r_iH) |+^n\rangle $$
- \(p_i\) and \(r_i\) optimized by external classical procedure
- Since the problem is encoded into the circuit - how to minimize resources needed?

\(H(t) = (1-t/T) \:H_{\rm mix} + t/T\: H\)
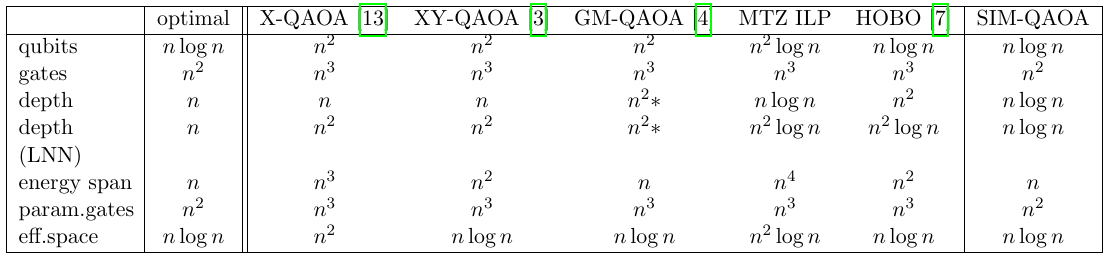
Quality measures
number of physical qubits
effective space size
number of gates
number of parm. gates
depth
depth on LNN
energy span

log(# solutions)
log(# solutions)
# degrees of freedom
# degrees of freedom
# degrees of freedom/log(# solutions)
# degrees of freedom/log(# solutions)
max(obj. value) - min(obj. value)
measures
lower bounds
Max-\(K\)-Cut


Minimal example
- \(-\prod_{i=1}^n b_i\)
- Corresponding Ising model: \( -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\)
- exponential number of terms \(O(2^n)\)!


\(O(n^2)\) gates on LNN!
\(b_i \leftarrow \frac{1-s_i}{2}\)
SIM-QAOA
This is AND operation!

Was it interesting?
- we reached optimal quality measures
- we essentially dropped the dependency on \(K\)
- fits very well NISQ requirements!
- very important problem!
- we essentially took Fuchs idea and have simply chosen better initial state...
Let's go with a harder problem - Travelling Salesman Problem!
YES
NO

Travelling Salesman Problem
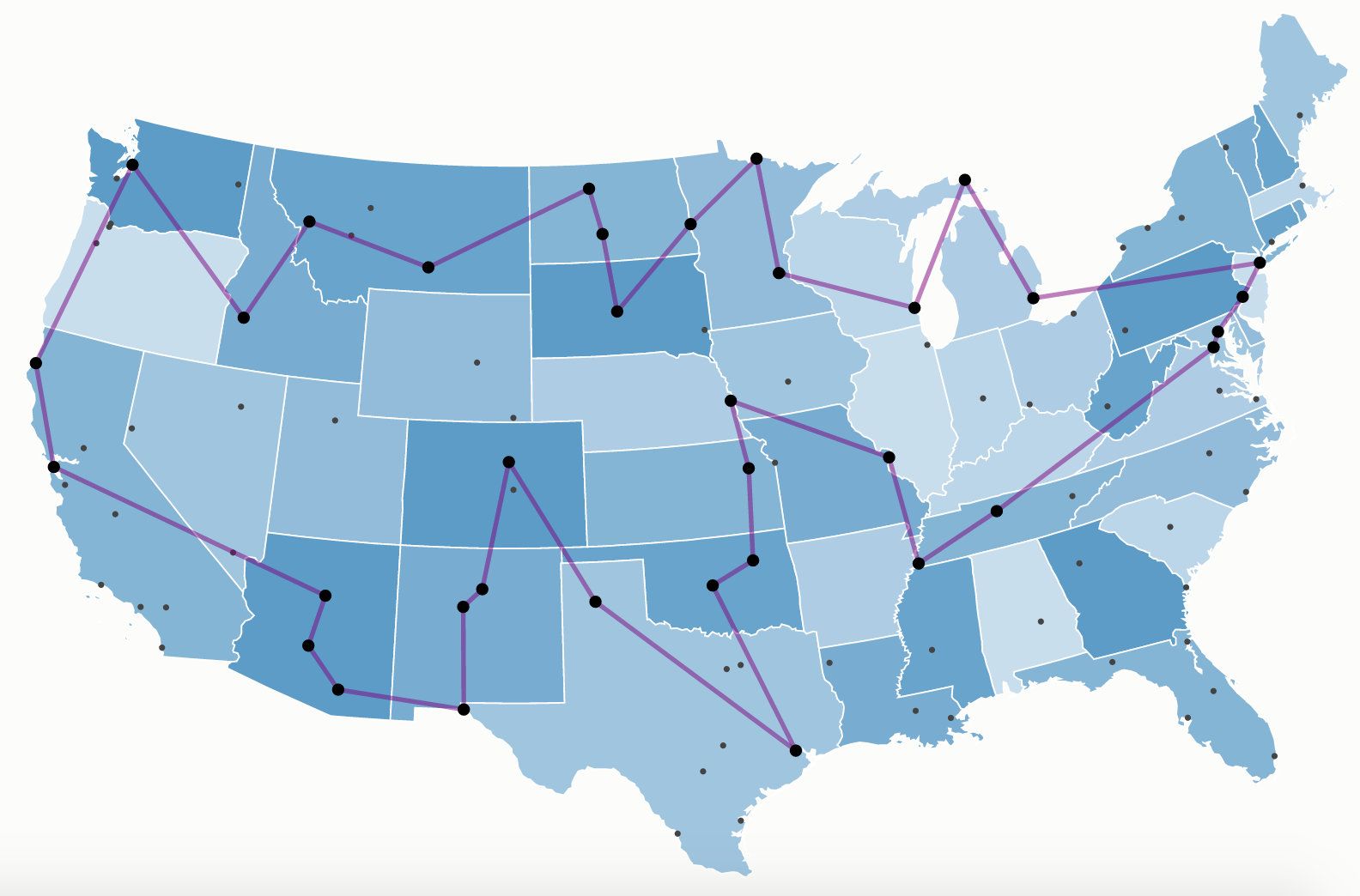
\(w_{ij}\)
TSP - redundancy

Time 2
City 3
}
cost
matrix
}
cost
matrix
}
cost
matrix
}
cost
matrix
}
cost
matrix

Travelling Salesman Problem
-
None of the encodings matches the "natural optimal" value, ...
-
..., but none can! We repeated \(O(n^2)\) degrees of freedom \(n\) times - \(O(n^3)\) gates

MTZ ILP is an exception, as variables are not "time to city" but "city to city"
SIM-QAOA for TSP
- We start in the superposition of valid cities for each time-point
- we choose Grover Mixer for our purpose (different ones can be used)
- Hamiltonian implemented through a quantum version of the classical pseudocode (with some parallelization + swapping strategy)
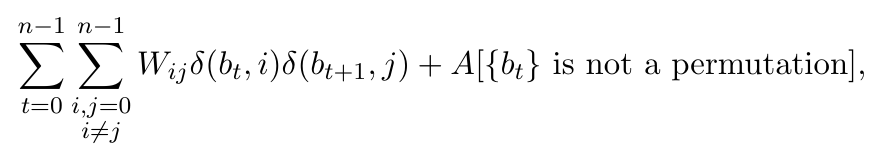
TSP - SIM-QAOA


TSP - SIM-QAOA


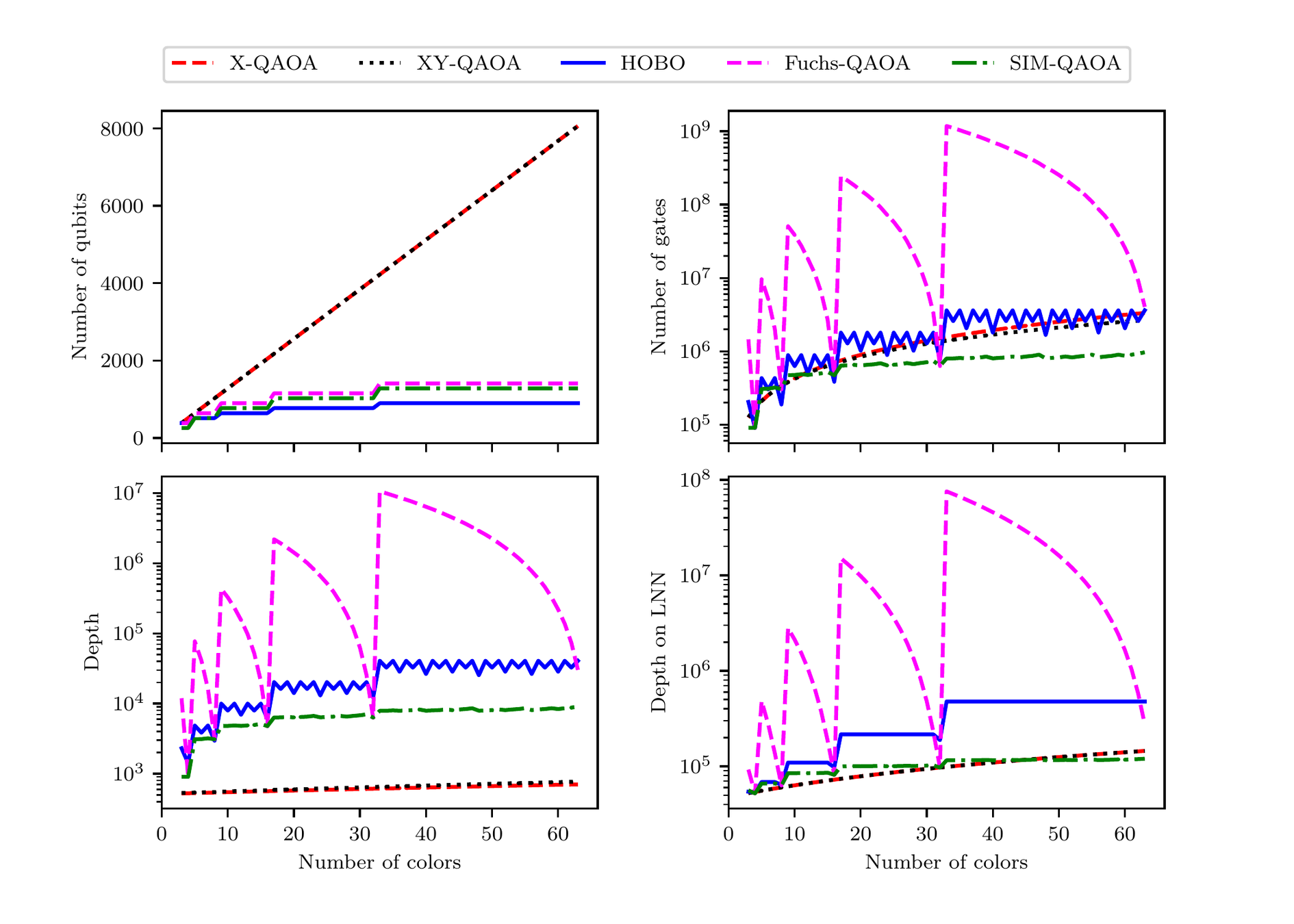
TSP - numerics
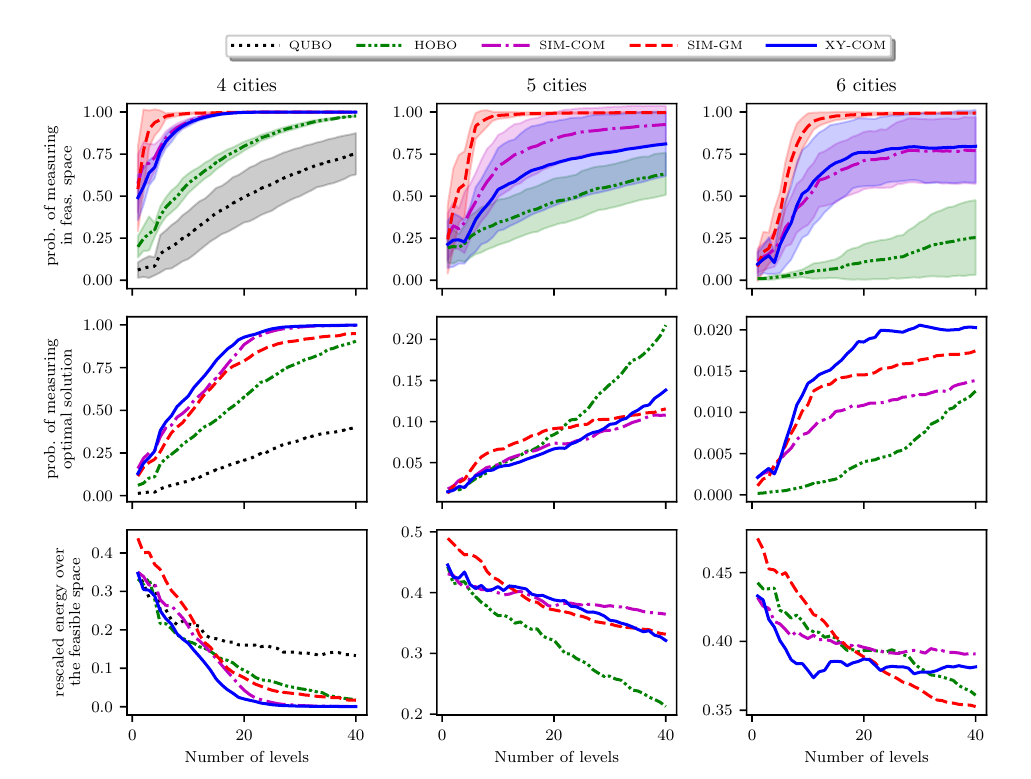
GM-QAOA clearly better!



...but at a price
Generalization
The idea can be generalized, so far we managed to use it for
- Set Cover problem
- Integer Linear Problem (trade-off)
- Graph Isomorphism (trade-off in general, optimal for Euclidean graphs)

Very difficult for general graph!
Thank you!
-
Bärtschi, Andreas, and Stephan Eidenbenz. "Grover mixers for QAOA: Shifting complexity from mixer design to state preparation." 2020 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2020.
-
Fuchs, Franz G., et al. "Efficient Encoding of the Weighted MAX-\(K\)-CUT on a Quantum Computer Using QAOA." SN Computer Science 2.2 (2021): 1-14.
-
Glos, Adam, Aleksandra Krawiec, and Zoltán Zimborás. "Space-efficient binary optimization for variational quantum computing." npj Quantum Information 8.1 (2022): 1-8.
-
Wang, Zhihui, et al. "XY mixers: Analytical and numerical results for the quantum alternating operator ansatz." Physical Review A 101.1 (2020): 012320.
-
Lucas, Andrew. "Ising formulations of many NP problems." Frontiers in physics (2014): 5.
-
Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014).
simultaneous reduction - short
By Adam Glos
simultaneous reduction - short
- 255



