Joint Estimation and Inference for Data Integration Problems based on Multiple Multi-layered Gaussian Graphical Models
Subhabrata Majumdar & George Michailidis
Presenter: Aiying Zhang
April 25th, 2018
Content
- Introduction
- Statistical Model
- Algorithm
- Testings
- Performance evaluation
- Discussion
Goal:
Build a framework based on Gaussian Graphical Model (GGM) for horizontal and vertical integration of information across multi-omics data.
Horizontal: multi-conditions/subtypes
Vertical： different omics
Omics: genomic, proteomic, metabolomic
Contribution：
Borrow information across multiple similar multi-layer networks to simultaneously perform inference on all model parameters.
Introduction
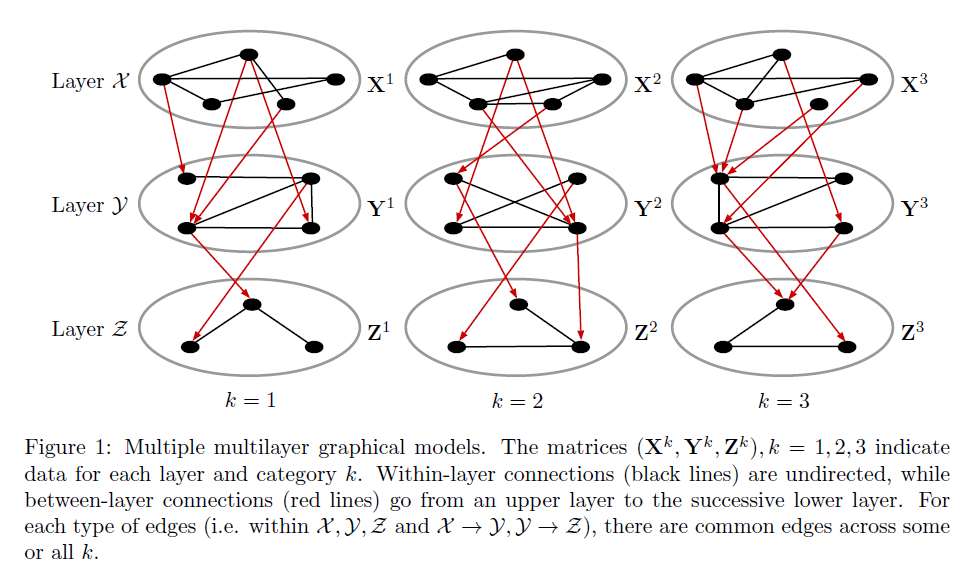
Introduction
- Joint Multiple Multi-Layer Estimation (JMMLE)
- Hypothesis testing in multi-layer models
- Dataset D, K groups, M layers
- Each layer m has pm variables(nodes)
- Model: for each group k=1,...,K
- Parameters of interest :
- the precision matrices
- the coefficient matrices
JMMLE
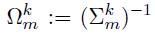
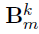
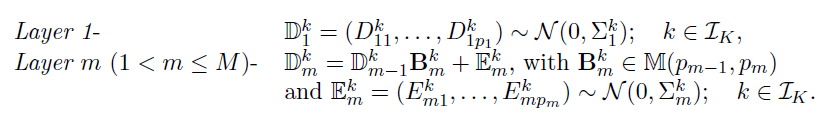
- Special case -- a two-layer model: M=2
- Goal: estimate from
- Focus: joint estimation of
- Noted:
- For M>2, within-layer undirected edges of any m-th layer(m>1) and between-layer directed edges (m-1)-th layer can be estimated by the same method.
- Joint estimation of can use other existing methods.
JMMLE
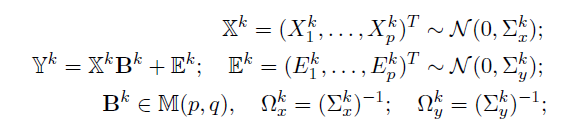
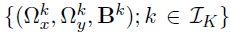
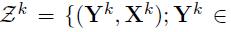
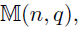
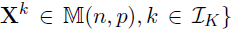
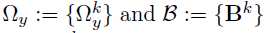
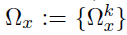
Algorithm
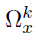
Estimation of
- Joint Structural Estimation Method (Ma and Michailidis, 2016)
- Use penalized nodewise regressions to get the graph structure
- Obtain neighborhood matrix
- Fit a graphical lasso model to obtain the sparse estimates of the precision matrix
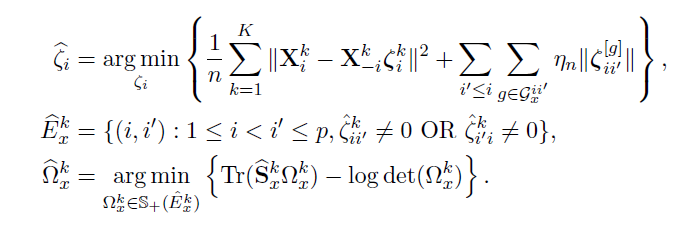
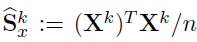
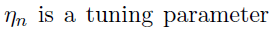
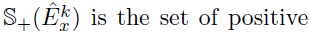
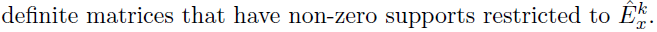
Algorithm
Joint estimation of
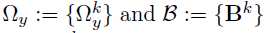
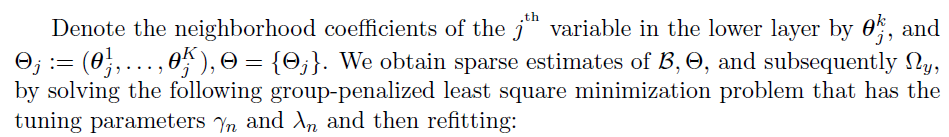
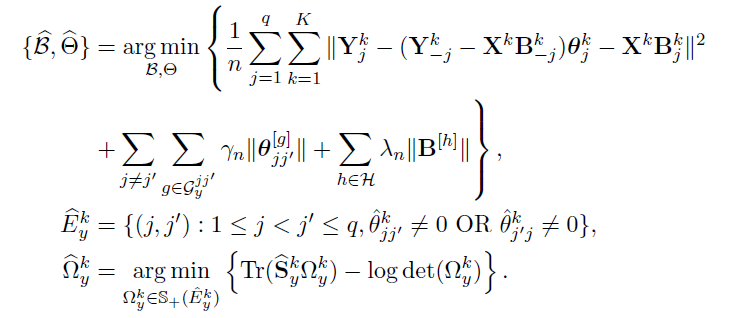
Algorithm
Alternative Block Algorithm:
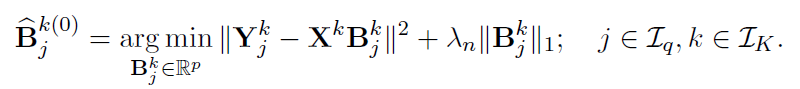
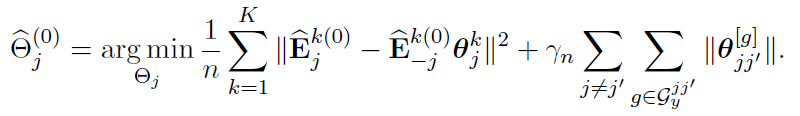
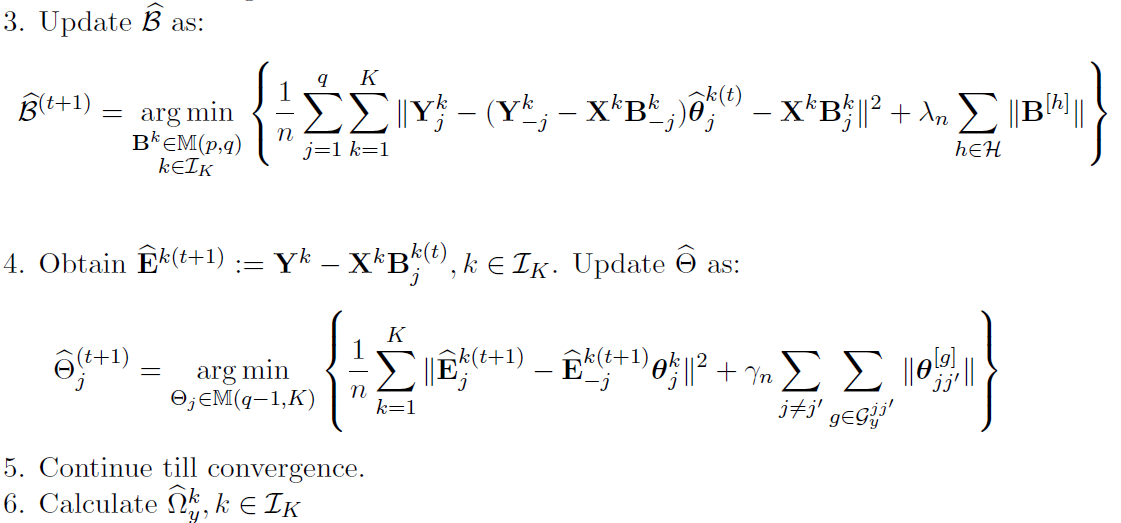
Algorithm
Tuning parameter selection:
- BIC (Bayesian Information Criterion) for
- HBIC (High-dimensional BIC) for
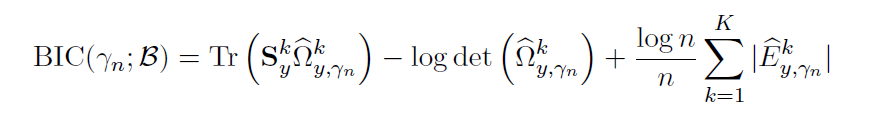
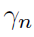
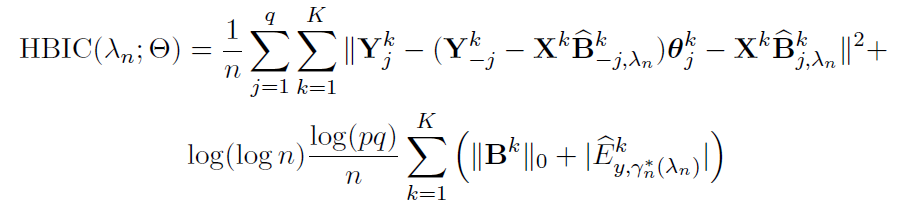
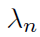
Hypothesis testing
Debiased estimator and asymptotic normality
- Proposed by Zhang and Zhang (2014)
- A debiasing procedure for lasso estimates for individual coeffcients in high-dimensional linear regression
- Method:
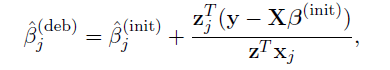
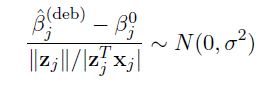
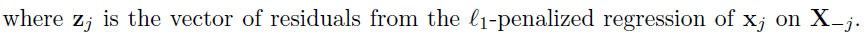
Hypothesis testing
Debiased estimator
- Define debiased estimates for individual rows of
- Under mild conditions, a centered and scaled
are asymptotic normal.
(\hat{c}_i^1,...,\hat{c}_i^K)
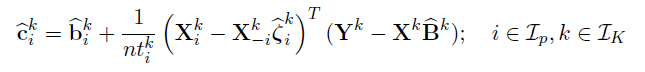
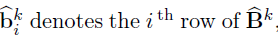
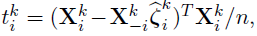
Hypothesis testing
Pairwise testing
- Global differences between two groups
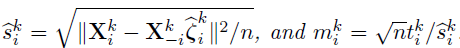
Hypothesis testing
Entrywise differences
- Test statistics:
- FDR control: Benjamini-Hochberg (BH) procedure
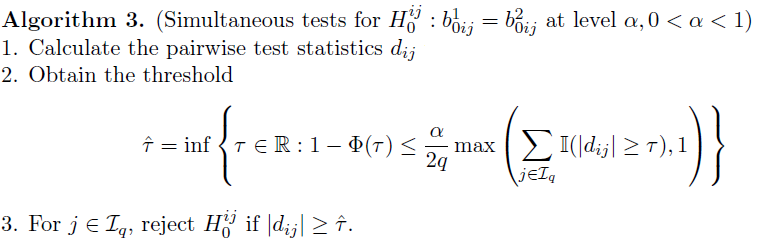
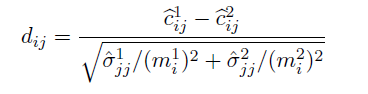
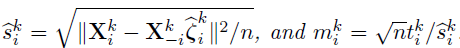
Performance
Evaluation
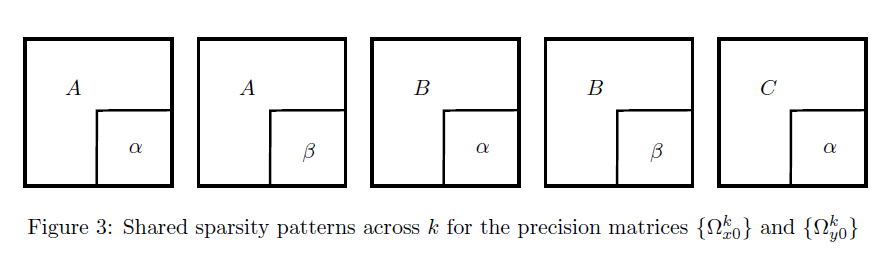
- K=5, M=2
- Within-layer: non-zero probability
- Between-layer: non-zero probability
- Non-zero elements independently from the uniform distribution
- 50 replications in each setting
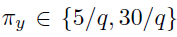
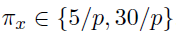
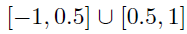
Performance
Evaluation
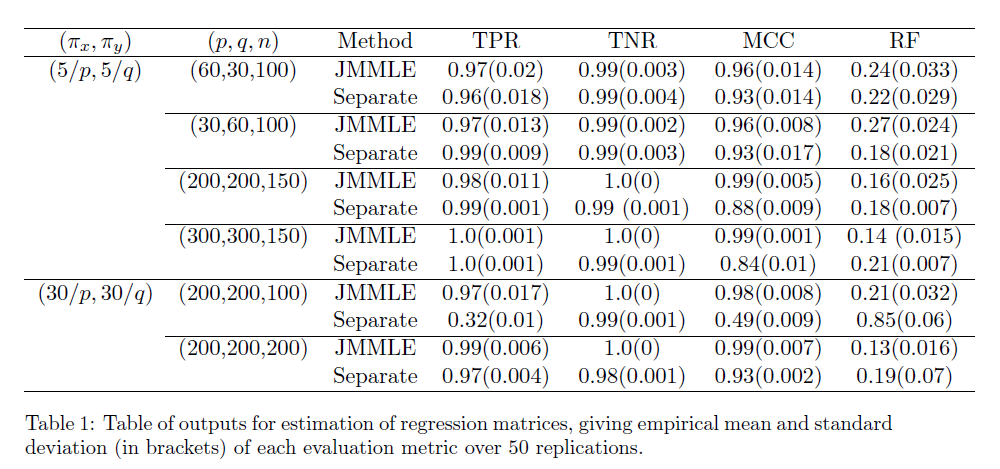
MCC: Matthews Correlation Coefficient
RF: Relative error in Frobenius norm
Performance
Evaluation
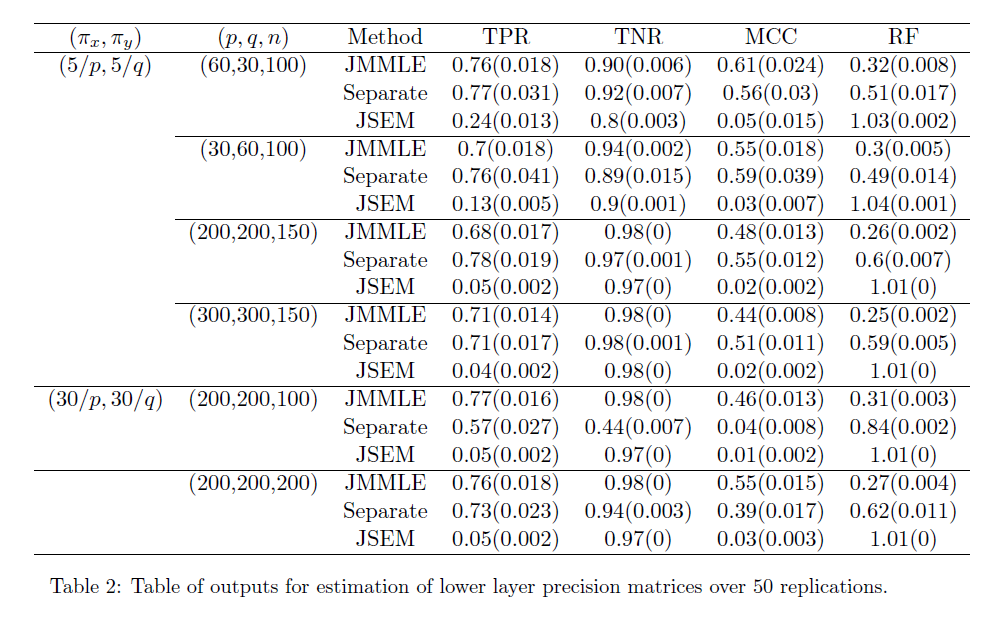
Performance
Evaluation
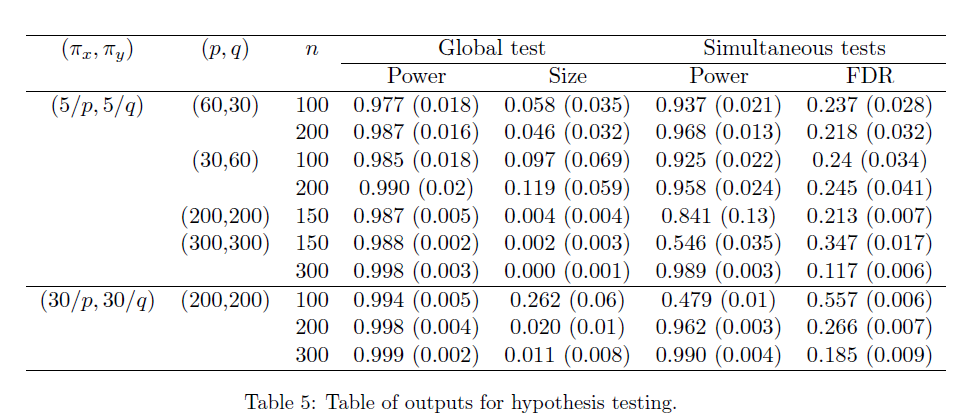
Simulation 2: Testing
- K=2
- Generate the by randomly assigning each element to be non-zero with probability , then drawing values of those elements from Unif{ }.
- Generate a matrix of differences D, where takes values -1, 1, 0 w.p. 0.1, 0.1, 0.8, respectively.
- Finally, set
Type-1 error set , FDR controlled at
\pi
(D)_{ij}
\alpha = 0.05
\beta = 0.2
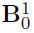
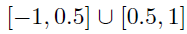
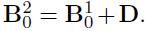
Performance
Evaluation
Discussion
Conclusions:
- This work introduces an integrative framework for knowledge discovery in multiple multi-layer Gaussian Graphical Models.
- Exploit a priori known structural similarities across
parameters of the multiple models - Perform global and simultaneous testing for pairwise differences
- Exploit a priori known structural similarities across
Improvements:
- Beyond pairwise testing, need an overall test for multi-groups
- Non-Gaussian data and graphical models with non-linear interactions
Joint Estimation and Inference for Data Integration Problems based on Multiple Multi-layered Gaussian Graphical Models
By Aiying Zhang
