Probabilistic Counting
Problem
Counting things is difficult,
especially when you have a lot of things to count.
The number of items in a set is its cardinality.
A list can have duplicate entries, a set cannot.

Problem
MongoDB Ids are represented by 24 character strings (24 bytes):
56def5418e80271df973a9a7
We get about 3000 requests per minute, containing account, event, campaign, segment, user, audience, creative, landing page, etc. IDs.
~43 Million ID events per day
Just the IDs represent 24 bytes * 43 Million = 1 GB per day.
After 1 year, we'd need 365 GB of RAM ~ $10k / month in counting servers
Bitmaps
Linear Counting
HyperLogLog
Bitmap
Make a list of 0s, as long as the maximum cardinality of your set. (Let's say 43 million for us)
Create a function that maps our ids to a unique number between 0 and 43 million.
When you encounter an ID, set that n-th number to 1 (from 0).
Bitmap
43 Million * 1 bit = 5.375MB (instead of 1GB per day)
Problems are:
- It's still wasteful
- Our cardinality is much higher than 43 million
- Hashing functions with randomly decided, uniformly distributed ranges don't exist.
Linear Counter
"A Linear-Time Probabilistic Counting Algorithm for Database Applications "
Whang, et. al. 1990
Start with much smaller bitmap (smaller than the size of your cardinality)
m = size of the mask
w = weight of the mask
n = estimate of cardinality
Linear Counter
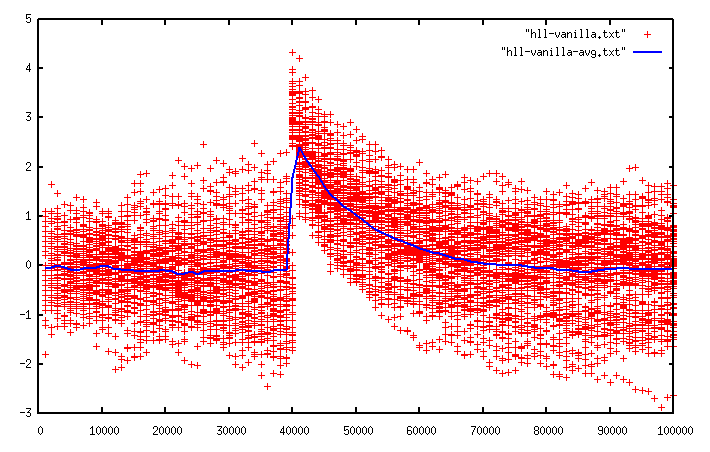
First counter which is not perfectly accurate.

Counting distinct words used
in all of Shakespeare's work
- Bitmap
- Size: 10.4 Million Bytes
- Count: 67,801
- Linear Counter
- Size: 3.3k Bytes (99.97% reduction)
- Count: 67,080 (~1% Error)
HyperLogLog
This one is cray (the paper is ~50 pages long)
Bitmaps and Linear Counters contain information about members of the set
That can be improved!
(Data -> Hashed -> Number -> Value at index of that number is flipped)

How many coins did I flip?
What's the longest run of heads you had?
- 1
- You didn't flip very many coins
- 5
- You were probably flipping for a while
-
1000
- You've been flipping coins your whole
life
- You've been flipping coins your whole
HyperLogLog
- Hash incoming data to a number
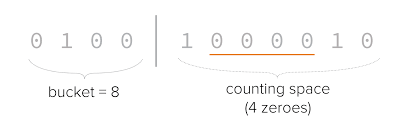
- Convert it to base 2 (binary):
100101011010001
- Use the left-most 4 digits to index into a bucket. The remaining get counted for runs of zeroes.
- HLL only keeps track of the longest run of 0s for that bucket
HLL Shakespeare

Shakespeare Count
- Bitmap
- Size: 10.4 Million Bytes
- Count: 67,801 (0% error)
- Linear Counter
- Size: 3.3k Bytes (99.97% reduction)
- Count: 67,080 (~1% error)
- HyperLogLog
- Size: 512 Bytes (99.995% reduction)
- Count: 70,002 (~3% error)
For Feathr
99.995% * 365 GB
= 18.25MB!*
*Not actually true since we're using HLLs with a fixed 0.8% error, which are ~16KB and not 512 Bytes
Probabilistic Counting
By Aleksander Levental
Probabilistic Counting
- 483

