Arquitectura

De

>

_

Computadoras

Dr. Alfredo de Jesús Gutiérrez Gómez

Presentación

Instrucciones para la presentación

1. Piense en el nombre de un animal que inicie con la primera letra de su nombre.

2. Este no deberá repetirse.

3. Al presentarse deberá completar la siguiente frase: Mi nombre es: _______ y he venido sobre un/a: _______ a la escuela desde _____

4. Dar respuesta a las preguntas:

4.1 ¿Porqué estudio está carrera?

4.2 ¿Qué me ha gustado de la carrera hasta ahora?

Temas del curso

Unidad 1. Sistemas de números

1.1 Sistemas posicionales.
1.2 Representación polinomial.
1.3 Representación yuxtaposicional. 1.4 Conversión entre bases.
1.5 Base 10 a cualquier base.
1.6 Cualquier base a base 10.
1.7 Conversión de base "r" a base "s".

Temas del curso

Unidad 2. Códigos de representación de datos.

2 2.1 código ASCII.
2.2 código bcd.
2.3 código ebcdic.

2.4 código baudot. 2.5 código gray.

Temas del curso

Unidad 3 Diseño de la unidad aritmética lógica.

3.1 Analizar la teoría básica de una unidad aritmética-lógica utilizando los conceptos de: magnitud y signo, complementos a uno y complementos a dos.
3.2 Diseñar una unidad aritmética-lógica a nivel de compuertas lógicas.

Temas del curso

Unidad 4 Sistemas de memoria.

4.1 Memoria principales.

4.2 Memoria cache.
4.3 Memoria externa.

Temas del curso

Unidad 5 Microprogramación.

5.1 definir los componentes básicos de un controlador microprogramable
5.2 especificar las líneas de interconexión entre el controlador microprogramable y las partes a controlar.
5.3 definir la palabra de control de acuerdo a las especificaciones de un problema dado.
5.4 diseñar controladores microprogramables para ejemplos específicos.

Temas del curso

Unidad 6 Diseño de una computadora básica.

6.1 integrar los conocimientos diseñando una computadora básica.
6.2 diseñar la unidad de control de la computadora básica con el método de microprogramación.

Temas del curso

Unidad 7 Conceptos generales sobre arquitecturas computacionales.

7.1 Evolución de las arquitecturas de computadoras.
7.2 Máquinas cisc.
7.3 Máquinas risc.

7.4 Comparación cisc vs. risc.

7.5 Arquitecturas paralelas.

Políticas de clase

Teléfono móvil en modo silencio.
Las llamadas urgentes /prio se contestan fuera del salón.
Turnos de una sola persona para ir al WC.
Dos faltas a la semana sin justificante perderían derecho a las cuestiones de aprendizaje.
Levantar la mano para participar.
Respetar la participación de cada alumno.

Lineamientos de clase

Mantenerse informado acerca de las lecturas, actividades y tareas del curso asistiendo por lo menos dos veces por semana, durante la duración del curso.
Cumplir dentro del aula virtual con todas las tareas, foros y actividades detalladas por el programa académico y el profesor, en el tiempo y forma establecidos.
El incumplimiento de las tareas en tiempo y forma llevarán a una no aprobación del curso.

Lineamientos de clase

Realizar el seguimiento personal desde el Aula Virtual.
Estar pendiente de los resultados de las evaluacion/es parcial/es y final/es.
Notificar al tutor por escrito, con copia a la coordinación académica, si, por alguna razón excepcional, se encontrara en una circunstancia especial que le impidiera continuar con el curso y recibir así indicaciones de cómo proceder a partir de ese momento.

Descripción de las actividades

Unidad 1 Sistemas de números

Tabla comparativa
Cuestionamientos de aprendizaje.

Descripción de las actividades

Unidad 2 Códigos de representación de datos.

Caso de estudio.
Cuestionamientos de aprendizaje

Descripción de las actividades

Unidad 3 Diseño de la unidad aritmética lógica.

Solución de Ejercicios.
Cuestionamientos de aprendizaje.

Descripción de las actividades

Unidad 4 Sistemas de memoria.

Tabla comparativa
Cuestionamientos de aprendizaje.

Descripción de las actividades

Unidad 5 Microprogramación.

Reporte de investigación
Cuestionamientos de aprendizaje.

Descripción de las actividades

Unidad 6. Diseño de una computadora básica.

Estudio de casos
Cuestionamientos de aprendizaje.

Descripción de las actividades

Unidad 7 Conceptos generales sobre arquitecturas computacionales.

Estudio de casos
Cuestionamientos de aprendizaje.

Actividades de encuadre

Instrucciones:

En una hoja escribe la respuesta a la siguiente pregunta:
1. ¿Qué esperas que se enseñe en este curso?

Tiempo de la actividad: 6 minutos.

Actividades de encuadre

Instrucciones:

Debajo de la pregunta anterior responde la siguiente cuestión:
1. ¿A qué te comprometes en este curso?

Tiempo de la actividad: 6 minutos.

Actividades de encuadre

Instrucciones:

Debajo de la pregunta anterior responde la siguiente cuestión:
1. ¿Qué deseas aprender en este curso?

Tiempo de la actividad: 6 minutos.

Actividades de encuadre

Una vez contestadas las preguntas anteriores escribir en el foro respectivo la respuesta a cada pregunta.

Tiempo de la actividad: 6 minutos.

Recomendaciones para las actividades

Trabajos:

Presentación / portada
Introducción
Conclusión

Párrafos:

Mayores a tres líneas
Menores a ocho líneas
Coherencia entre párrafos

Ortografía - Gramática

Acentuación.
Evitar redundancia.
Pleonasmos.
Mínimo tres errores.

Recomendaciones para las actividades

Referencias bibliográfica

Al menos tres citas dentro del trabajo.
En formato APA 7ma edición.

Lista referencia bibliográfica

Al menos tres fuentes de diversos autores.
Con sangría francesa al inicio de cuatro espacios.
Fuente Times New Roman.
12 puntos.
Sin enlaces activos.

Recomendaciones para las actividades

Introducción y conclusión

Al menos tres párrafos.

Formato del trabajo

Fuente Arial.
Tamaño de título: 14 puntos.
Tamaño de texto: 12 puntos.
Interlineado 1.5
Alineación justificada del texto.
Los títulos alineados a la izquierda.
En el encabezado del documento colocar el logotipo del instituto alineado a la derecha. Nombre de la carrera a la izquierda.

Recomendaciones para las actividades

Diagramas:

Hacerlos en día.
Exportarlos a jpg / png

Códigos fuentes:

Colocarlos en github.
En el documento a entregar, colocar el enlace al código.

Tablas:

Colocarle al pie de la tabla un nombre a la tabla, bajo el siguiente formato: <Tabla numero consecutivo>. <nombre_tabla> .<Fuente:> <donde_fue_tomada> .
Colocar un párrafo descriptivo de la tabla.

Ejemplo recomendado para el uso de tablas

IA I	POO	P. batch
10	10	8
19	6	9

Tabla 1. Listado de materias con calificaciones obtenidas en cada actividad. Fuente: Creación propia

En la tabla 1, se puede apreciar tres materias donde se encuentra las calificaciones obtenidas en dos actividades realizadas en cada una de ellas. Para calcular el promedio solo se debe de sumar cada actividad en un nuevo renglón y dividirlo entre dos que son el número de actividades.

Ejemplo recomendado para el uso de tablas

IA I	POO	P. batch
10	10	8
19	6	9

Tabla 1. Listado de materias con calificaciones obtenidas en cada actividad. Fuente: Tomada del libro Introducción a la programación de Luis Joyanes Aguilar. P.19.

Recomendaciones para las actividades

Imagenes / diagramas / gráficas:

Colocarle al pie de la imagen / diagrama / gráfica un nombre, bajo el siguiente formato: <nombre_objeto numero consecutivo>. <nombre_objeto> <fuente:> <donde_fue_tomada> .
Colocar un párrafo donde se describa la imagen / diagrama / gráfica

Recomendaciones para el uso de imágenes / gráficas / diagramas

Imagen 1. Fachada de una casa. Fuente: Creación propia

En la imagen 1 se puede observar la fachada de una casa convencional donde. Lo que permite poder llevar acabo construcciones básicas pero eficientes, con canaletas para la recolección de agua pluvial y su posterior tratamiento.

Recomendaciones para el uso de imágenes / gráficas / diagramas

Imagen 1. Fachada de una casa. Fuente: Tomado del libro Diseños y principios básicos de arquitectura de Ruben Vazquez

¿Dudas / Preguntas / comentarios?

Temas

Sistemas de números.
Sistema posicional.
Representación polinomial.
Representación yuxtaposicional.
Conversión entre base.
De base 10 a cualquier base.
Cualquier base a base 10.
Convertir de base "r" a base "s"

Sistema de números

Morris Kline

Un sistema de números es un conjunto de símbolos y reglas que permiten representar y manipular cantidades numéricas. Proporciona una estructura para organizar y expresar las magnitudes y relaciones numéricas

John D. Bowers

Un sistema de números es un conjunto de elementos y operaciones definidos sobre esos elementos, que nos permite representar y manipular cantidades y realizar cálculos matemáticos

Definiendo un sistema de números

Actividad de aprendizaje

Define tu concepto

Visita www.frexus.dev/slide
Pulsa en el enlace de la materia (arquitectura de computadoras)
Busca la opción que diga "Actividades de aprendizaje", pulsa en el enlace.
Crea una tabla donde presentes tres definiciones del concepto sistema de números y tu propia definición.

Sistemas Posiconales

Actividad de aprendizaje

Define ¿qué es para ti un sistema posicional?
En la hoja de calculo de ethercalc escribe tu definción.

Sistema deciamal

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Unidad	Decena	Centena
3
3	6
3	6	9

Actividad de aprendizaje

Del siguiente listado de números colocadlos en sus respectivas unidades, decenas y demás

Números:

36
369
9321032392
039

Nota: El sistema posicional permite representar números de cualquier magnitud utilizando un conjunto limitado de dígitos y reglas simples.

Representación

polinomial

¿Qué es la representación polinomial?

Autores Diversos

Es una forma de expresar un número utilizando una combinación de potencias de una base dada. En esta representación, cada dígito en el número se multiplica por la potencia correspondiente de la base y se suman todos los términos para obtener el valor total del número.

Representación polinomial

369 = 3*10^2 + 6*10^1 + 9*10^0

centena (2)	decena (1)	unidad (0)
3	6	9
Base:	10

Actividad de aprendizaje

39
936
3242
98328

Realiza la representación polinomial de los siguientes números:

Representación Yuxtaposicional

¿Qué es la representación yuxtaposicional?

Es un método de representación de números en el que los dígitos se colocan uno al lado del otro en secuencia para formar el número completo.

¿Qué caracteristicas tiene la representación yuxtaposicional?

Cada dígito tiene un valor que depende de su posición relativa en el número.
La posición de un dígito se determina por su distancia con respecto al punto decimal (o coma en algunos países), que divide la parte entera de la parte fraccionaria del número.
Los dígitos a la izquierda del punto decimal representan la parte entera.
Los dígitos a la derecha del punto decimal representan la parte fraccionaria.

Ejemplo

El número 369.96

Centenas	Decenas	Unidad	Decimas	Centécimas
3	6	9	9	6

Actividad de aprendizaje

3.23
3,936.28
936.39
369.9632
9,369,963.28

Realiza la representación yuxtaposicional de los siguientes números:

La representación yuxtaposicional permite representar números de cualquier magnitud y precisión utilizando un conjunto limitado de dígitos y reglas de posición relativa.

Conversión entre bases

¿Qué es la conversión entre bases?

Se refiere al proceso de cambiar la representación de un número de un sistema numérico con una base específica a otro sistema numérico con una base diferente.

Consiste en transformar un número de una base a otra base, manteniendo el valor numérico original.

Es decir, que...

Pasos para convertir de base 10 a binario.

Se realiza dividiendo sucesivamente el número decimal entre 2 y tomando los residuos en cada paso.
Los residuos se concatenan en orden inverso para formar el número binario equivalente.

Ejemplo

Numero	Base	Operación	Resultado	Residuo
33	2	33 ÷ 2	16	1
		16 ÷ 2	8	0
		8 ÷ 2	4	0
		4 ÷ 2	2	0
		2 ÷ 2	1	0
		1 ÷ 2	0	1

Convertir el número 33 de base 10 a su representación en base 2

33 de base 10 su base binaria es: 100001

Ejemplo

Numero	Base	Operación	Resultado	Residuo
25	2	25 ÷ 2	12	1
		12 ÷ 2	6	0
		6 ÷ 2	3	0
		3 ÷ 2	1	1
		1 ÷ 2	0	1

Convertir el número 25 de base 10 a su representación en base 2

25 de base 10 su base binaria es: 11001

Actividad de aprendizaje

Realiza la conversión de los siguientes números de base 10 a base 2

De base 10 a base 8

Se realiza dividiendo sucesivamente el número decimal entre 8 y tomando los residuos en cada paso.
Los residuos se concatenan en orden inverso para formar el número octal equivalente.

Ejemplo

Numero	Base	Operación	Resultado	Residuo
52	8	52 ÷ 8	6	4
		6 ÷ 8	0	6

Convertir el número 52 de base 10 a su representación en base 8

25 de base 10 su base octal es: 64

Ejemplo

Numero	Base	Operación	Resultado	Residuo
572	8	572 ÷ 8	71	4
		71 ÷ 8	8	7
		8 ÷ 8	1	0
		1 ÷ 8	0	1

Convertir el número 572 de base 10 a su representación en base 8

572 de base 10 su base octal es: 1074

Actividad de aprendizaje

Realiza la conversión de los siguientes números de base 10 a base 8

De base 10 a base 16

Se realiza dividiendo sucesivamente el número decimal entre 16 y tomando los residuos en cada paso.
Convierte los residuos obtenidos en cada paso a dígitos hexadecimales según la siguiente correspondencia: 10 = A, 11 = B, 12 = C, 13 = D, 14 = E, 15 = F.
Los residuos se concatenan en orden inverso para formar el número hexadecimal equivalente.

Ejemplo

Numero	Base	Operación	Resultado	Residuo
333	16	333 ÷ 16	20	13
		20 ÷ 16	1	4
		1 ÷ 16	0	1

Convertir el número 333 de base 10 a su representación en base 16

333 de base 10 su base octal es: 14D

Actividad de aprendizaje

Realiza la conversión de los siguientes números de base 10 a base 16

Base 10 a cualquier base

Pasos para convertir un número de base decimal a cualquier base

De base 10 a cualquier base

Divide el número decimal por la base deseada y obtén el cociente y el residuo.
El residuo obtenido se representa como un dígito en la nueva base.
Si el cociente obtenido en el paso anterior es mayor que 0, repite los pasos 1 y 2 utilizando el cociente como nuevo número decimal.
Si el cociente actual es 0, detén el proceso.
Escribe los dígitos obtenidos en el orden inverso en el que fueron calculados. Estos dígitos formarán el número en la nueva base.

Ejemplo

Numero	Base	Operación	Resultado	Residuo
369	5	369 ÷ 5	73	4
		73 ÷ 5	14	3
		14 ÷ 5	2	4
		2 ÷ 5	0	2

El número 369 de base 10 convertido a base 5 es: 2434

Convertir el número 369 de base 10 a base cinco

Ejemplo

Numero	Base	Operación	Resultado	Residuo
369	6	369 ÷ 6	61	3
		61 ÷ 6	10	1
		10 ÷ 6	1	4
		1 ÷ 6	0	1

El número 369 de base 10 convertido a base 6 es: 1413

Convertir el número 369 de base 10 a base 6

Actividad de aprendizaje

Realiza la conversión de los siguientes números de base 10 a base 3, 4, 5, 6, 7, 8, 9, 15, 16

635
6
9
369
963
939128

Cualquier base a base 10

Pasos para convertir de cualquier base a base 10

De derecha a izquierda: multiplicamos la primera cifra por 1 (1 es 80) ; la segunda, por 8 (8 es 81); la tercera, por 82; la cuarta, por 83. Y así hasta que hayamos multiplicado todas las cifras.
Sumamos cada uno de los valores obtenidos.

Suponga que se tiene el número 156 de base ocho a base 10

Pasos para convertir de cualquier base a base 10

Suponga que se tiene el número 156 de base ocho a base 10

Num	*	Potencia	Operacion	Resultado
6	8	0	6*1	6
5	8	1	5*8	40
1	8	2	1*64	64
			Suma:	110

El numero 156 de base ocho convertido a base 10 es: 110

Pasos para convertir de cualquier base a base 10

Suponga que se tiene el número 3699 de base 9 a base 10

Num	*	Potencia	Operacion	Resultado
9	9	0	9 * 1	9
9	9	1	9 * 9	81
6	9	2	6 * 81	486
3	9	3	3 * 729	2187
				2763

El numero 3699 de base nueve convertido a base 10 es: 2763

Actividad de aprendizaje

Convierte los siguientes números de 6 a base 10

Convierte los siguientes números de 9 a base 10

Convierte los siguientes números de 3 a base 10

Conversión de base "r" a base "s"

Pasos para la conversión

Identificar la base del número.
Identificar a que base hay que convertirlo.
Convertir el número a base 10
Una vez el número este en base 10 pasadlo a la base que se solicita.

Pasos para convertir de cualquier base "r" a base "s"

Suponga que se tiene el número 399 de base 9 a base Hexadecimal

Num	*	Potencia	Operacion	Resultado
9	9	0	9 * 1	9
9	9	1	9 * 9	81
3	9	2	3 * 81	243
				333

El numero 399 de base nueve convertido a base 10 es: 333

Pasos para convertir de cualquier base "r" a base "s"

Suponga que se tiene el número 399 de base 9 a base Hexadecimal

El numero 333 de base nueve convertido a base 16 es: 14D

Numero	Base	Operación	Resultado	Residuo
333	16	333 ÷ 16	20	13
		20 ÷ 16	1	4
		1 ÷ 16	0	1

Actividad de aprendizaje

Convierte los siguientes números de 6 a base 9

Convierte los siguientes números de 9 a base 16

Convierte los siguientes números de 3 a base 5

Código de representación de datos

Temas

Código ASCII.
Código bcd.
Código ebcdic.
Código baudot.
Código gray.

Código

ASCII

ASCII

ASCII (American Standard Code for Information Interchange)

Sistema de codificación de caracteres ampliamente utilizado en computadoras y dispositivos electrónicos

Desarrollado en la década de 1960 como un estándar para representar caracteres en texto y comunicaciones.

¿qué es?

¿qué significa?

¿para que se creo?

¿Qué hace ASCII?

Asigna un número único a cada caracter, que va desde el 0 hasta el 127.
Los primeros 32 caracteres (0-31) se utilizan para controlar dispositivos y realizar acciones especiales, como el salto de línea o la retroalimentación del cursor.
Los siguientes 95 caracteres (32-126) representan caracteres imprimibles, como letras, números, símbolos de puntuación y caracteres especiales.

Para ¿qué sirve el ASCII?

Representación de caracteres:

Asigna un número único a cada caracter imprimible, como letras, números, símbolos de puntuación y caracteres especiales. Esto permite que los caracteres sean representados y almacenados en forma de bits, que son la base de la representación digital en los sistemas computacionales.

Procesamiento de texto

Procesa y manipula el texto. Los programas pueden realizar operaciones como búsqueda, ordenamiento, comparación y transformación de texto basándose en los valores numéricos del código ASCII de los caracteres.

Para ¿qué sirve el ASCII?

Interoperabilidad

Es un estándar ampliamente reconocido y utilizado a nivel mundial. Por lo que los sistemas y dispositivos que implementan el código ASCII pueden intercambiar información de manera consistente y sin problemas de compatibilidad.

Actividad de aprendizaje

En un blog de notas escribe:

# Conversión de caracter a código ASCII
caracter = 'A'
codigo_ascii = ord(caracter)
print(codigo_ascii)  # Output: 65

# Conversión de código ASCII a caracter
codigo_ascii = 66
caracter = chr(codigo_ascii)
print(caracter)  # Output: B

Guarde el fichero con el nombre ascii.py

Modifique el código para que reciba un carecter por el usuario y el script muestre el código ASCII correspondiente

Al terminar suba su código modificado al repositorio de github

Código BCD

¿Qué es el BCD?

Es un sistema de representación numérica en el que cada dígito decimal se representa con un grupo de cuatro bits (un número binario de 4 bits). En el código BCD, los valores del 0 al 9 se representan directamente con sus correspondientes patrones de 4 bits.

En el código BCD, cada uno de los cuatro bits de un grupo representa un dígito decimal en forma binaria. Por ejemplo, el número decimal 7 se representa como 0111 en BCD, donde cada dígito del código BCD representa el valor binario de cada dígito decimal. Este sistema permite una representación directa y precisa de los números decimales utilizando combinaciones de bits.

Ventajas del BCD

La principal ventaja del código BCD es que es fácil de entender y manipular para los humanos, ya que cada dígito decimal se representa de forma separada. Esto es especialmente útil en aplicaciones donde se requiere una alta precisión decimal, como en cálculos financieros y sistemas de visualización numérica.

Limitantes del BCD

una limitación del código BCD es que no utiliza de manera eficiente el espacio de almacenamiento o la capacidad de representación de los sistemas binarios. Dado que solo se utilizan los valores del 0 al 9 en cada grupo de 4 bits, hay un desperdicio de posibles combinaciones binarias. Por ejemplo, los números 10 a 15 no tienen una representación directa en BCD y requieren un sistema de codificación adicional para representarlos.

Tabla BCD

Digito Decimal	Representación en BCD (4 bits)
0	000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

Usando el BCD

Digito Decimal	Representación en BCD (4 bits)
3	0011
6	0110
9	1001

¿Cuál es la representación del número 369 en binario

La representación binaria del número 369 a binario es: 0011 0110 1001

Actividad de aprendizaje

Digito Decimal	Representación en BCD (4 bits)
9
7
6
3

Completa la siguiente tabla, de representación del número 9763 en binario

La representación binaria del número 9763 a binario es:

Código ebcdic

¿Qué es el código ebcdic?

El código EBCDIC (Extended Binary Coded Decimal Interchange Code)

Sistema de codificación de caracteres utilizado en sistemas informáticos y mainframes desarrollado por IBM en la década de 1960.

Diseñado principalmente para sistemas mainframe de IBM y algunos otros sistemas más antiguos

Ha sido reemplazado en gran medida por el código ASCII y otros estándares de codificación más modernos, debido a la mayor prevalencia y compatibilidad de ASCII en las computadoras y sistemas actuales

Características del código ebcdic

Utiliza 8 bits para representar cada caracter

Permite codificar hasta 256 símbolos diferentes

Tiene una estructura de asignación más compleja y menos intuitiva

Caracteres especiales y letras mayúsculas tienen diferentes valores que en el código ASCII

En EBCDIC, el código para la letra 'A' es 193, mientras que en ASCII es 65. Asimismo, otros caracteres tienen códigos diferentes en ambos sistemas.

Usando el código EBCDIC

import codecs

def ascii_to_ebcdic(text):
    try:
        # Codificación ASCII a EBCDIC (usando el mapeo CP500 de EBCDIC)
        ebcdic_text = codecs.encode(text, 'cp500')
        return ebcdic_text
    except Exception as e:
        print("Error:", e)
        return None

# Cadena de texto en formato ASCII
texto_ascii = "Hola, esto es un ejemplo de EBCDIC!"

# Convertir a EBCDIC
texto_ebcdic = ascii_to_ebcdic(texto_ascii)

if texto_ebcdic:
    print("Texto en formato EBCDIC:", texto_ebcdic)
else:
    print("La conversión a EBCDIC no pudo realizarse.")

Actividad de aprendizaje

Del código anterior modifiquelo para que reciba cualquier tipo de cadena de caracteres y muestre la codificación EBCDIC

Código baudot.

¿Qué es el código baudot?

conocido como código Murray o código ITA2 (International Telegraph Alphabet No. 2),

utilizado para la transmisión telegráfica.

inventado por Émile Baudot

uno de los primeros códigos ampliamente utilizados en las comunicaciones telegráficas.

diseñó originalmente para transmitir caracteres a través de una línea telegráfica mediante señales eléctricas

Características del código baudot

Cada carácter se representa mediante una secuencia de "bits.
Cada bit puede estar en uno de dos estados: "marcado" (1) o "espaciado" (0).
Cinco bits se usan para representar cada carácter, lo que permite un total de 32 combinaciones diferentes, suficiente para representar las letras del alfabeto, algunos símbolos y números.
Primero en utilizar un teclado con solo cinco teclas
sentó las bases para el desarrollo de códigos posteriores más sofisticados y eficientes.

Simulación baudot


baudot_table = {
    'A': '00011', 'B': '11001', 'C': '01110', 'D': '01001', 'E': '00001',
    'F': '10110', 'G': '11010', 'H': '00100', 'I': '00110', 'J': '10011',
    'K': '01010', 'L': '01100', 'M': '10010', 'N': '10000', 'O': '11000',
    'P': '10100', 'Q': '11100', 'R': '01101', 'S': '01011', 'T': '00101',
    'U': '11110', 'V': '10111', 'W': '01111', 'X': '11011', 'Y': '11101',
    'Z': '10101', ' ': '00000'}
def text_to_baudot(text):
    text = text.upper()
    encoded_text = ''
    for char in text:
        if char in baudot_table:
            encoded_text += baudot_table[char]
    return encoded_text
def baudot_to_text(encoded_text):
    decoded_text = ''
    for i in range(0, len(encoded_text), 5):
        baudot_char = encoded_text[i:i+5]
        for char, code in baudot_table.items():
            if baudot_char == code:
                decoded_text += char
                break
    return decoded_text
mensaje_original = "HELLO"
mensaje_codificado = text_to_baudot(mensaje_original)
mensaje_decodificado = baudot_to_text(mensaje_codificado)
print("Mensaje original: ", mensaje_original)
print("Mensaje codificado en Baudot: ", mensaje_codificado)
print("Mensaje decodificado: ", mensaje_decodificado)

Actividad de aprendizaje

Del código anterior:

¿Qué haría falta para que usara minúsculas y números?

¿Qué modificación se tendría que realizar para que acepte cualquier frase introducida por el usuario?

Código gray

¿Qué es el código gray?

Código reflejado

Sistema de codificación de números binarios

Inventado por Frank Gray en 1947

Ampliamente utilizado en electrónica digital y sistemas de comunicaciones

Cada número binario representa un valor decimal

Diseñado de tal manera que el cambio de un número a otro solo involucre la modificación de un solo bit

Minimiza las posibilidades de errores, ya que solo se produce un cambio de bit entre dos valores adyacentes.

Usos del código gray

Reducción de errores

Minimiza las posibilidades de errores en la interpretación de datos, especialmente en sistemas propensos a ruido o interferencias. Al cambiar solo un bit, se evita que un solo error en la transmisión cause cambios significativos en el valor representado, lo que mejora la fiabilidad y la precisión de los datos.

Estabilidad de señales

Proporciona una representación estable de los datos. En aplicaciones de control o en circuitos digitales que requieren transiciones suaves entre estados, evita glitches (pulso no deseado) y transiciones no deseadas que pueden ocurrir con otros sistemas de codificación. Útil en máquinas de estado finito y sistemas donde la precisión temporal y la estabilidad de las señales son críticas.

Usos del código gray

Eficiencia en la transmisión de datos

En sistemas de comunicaciones, es útil para reducir el número de errores de transmisión y mejorar la eficiencia del canal de comunicación. Al minimizar la probabilidad de errores de bit, se puede lograr una transmisión más robusta y confiable de los datos.

Aplicaciones específicas

Encuentra aplicaciones en áreas específicas como la codificación de sensores y encoders rotativos, donde se necesita una representación precisa de posiciones y mediciones. También es útil en sistemas de control y en ciertos algoritmos de compresión de datos.

Usos del código gray

diseño de circuitos digitales y sistemas de control

puede simplificar el diseño y reducir la complejidad. Al evitar situaciones de ambigüedad y glitches, se pueden reducir los circuitos adicionales requeridos para la corrección de errores y lógica de control, lo que lleva a diseños más eficientes y confiables.

Simulando el código gray

# Función para codificar un número decimal en código Gray
def codificar_gray(numero_decimal):
    return numero_decimal ^ (numero_decimal >> 1)
# Función para decodificar un número en código Gray al decimal original
def decodificar_gray(gray_numero):
    numero_decimal = gray_numero
    while gray_numero > 0:
        gray_numero >>= 1
        numero_decimal ^= gray_numero
    return numero_decimal
# Ejemplo de uso
numero_decimal_original = 42
# Codificación
codigo_gray = codificar_gray(numero_decimal_original)
print("Número decimal original:", numero_decimal_original)
print("Código Gray:", codigo_gray)
# Decodificación
numero_decimal_decodificado = decodificar_gray(codigo_gray)
print("Número decimal decodificado:", numero_decimal_decodificado)

Simulando el código gray

# Función para codificar un número decimal en código Gray
def codificar_gray(numero_decimal):
    return numero_decimal ^ (numero_decimal >> 1)
# Función para decodificar un número en código Gray al decimal original
def decodificar_gray(gray_numero):
    numero_decimal = gray_numero
    while gray_numero > 0:
        gray_numero >>= 1
        numero_decimal ^= gray_numero
    return numero_decimal
# Ejemplo de uso
numero_decimal_original = 42
# Codificación
codigo_gray = codificar_gray(numero_decimal_original)
print("Número decimal original:", numero_decimal_original)
print("Código Gray:", codigo_gray)
# Decodificación
numero_decimal_decodificado = decodificar_gray(codigo_gray)
print("Número decimal decodificado:", numero_decimal_decodificado)

Actividad de aprendizaje

Usando el código anterior, muestre la representación en codificación gray de los siguientes números:

Diseño de la unidad aritmética lógica.

Temas

Analizar la teoría básica de una unidad aritmética-lógica utilizando los conceptos de: magnitud y signo, complementos a uno y complementos a dos.
Diseñar una unidad aritmética-lógica a nivel de compuertas lógicas.

¿ALU?

Unidad Aritmética Lógica (ALU, por sus siglas en inglés: Arithmetic Logic Unit)

Es la encargada de realizar operaciones aritméticas (sumas, restas, multiplicaciones, divisiones, etc.) y operaciones lógicas (AND, OR, NOT, XOR, etc.) en datos binarios.

Los diseños pueden variar según la arquitectura y el conjunto de instrucciones del procesador

ALU BASICA

SUMA
RESTA
NOT
XOR

def alu(a, b, op):
    if op == "000":  # Suma
        return bin(int(a, 2) + int(b, 2))[2:].zfill(4)
    elif op == "001":  # Resta
        return bin(int(a, 2) - int(b, 2))[2:].zfill(4)
    elif op == "010":  # AND lógico
        return bin(int(a, 2) & int(b, 2))[2:].zfill(4)
    elif op == "011":  # OR lógico
        return bin(int(a, 2) | int(b, 2))[2:].zfill(4)
    else:
        raise ValueError("Operación no válida.")

# Ejemplo de uso
resultado_suma = alu("0110", "0011", "000")  # A = 6, B = 3, OP = 000 (Suma)
resultado_resta = alu("0110", "0011", "001")  # A = 6, B = 3, OP = 001 (Resta)
resultado_and = alu("0110", "0011", "010")  # A = 6, B = 3, OP = 010 (AND)
resultado_or = alu("0110", "0011", "011")  # A = 6, B = 3, OP = 011 (OR)

print("Resultado de la suma:", resultado_suma)
print("Resultado de la resta:", resultado_resta)
print("Resultado del AND:", resultado_and)
print("Resultado del OR:", resultado_or)

Actividad de aprendizaje

Del código anterior muestre los resultados de suma, resta, or y and de los siguientes números decimales:

Valores para a:

333

666

999

valores b:

132

936

777

DISEÑO ALU

Analizar la teoría básica de una unidad aritmética-lógica utilizando los conceptos de: magnitud y signo, complementos a uno y complementos a dos.

Teorías para el diseño de ALU

Diseño basado en instrucciones y conjuntos de operaciones

La ALU debe estar diseñada para admitir el conjunto de instrucciones del procesador en el que se utilizará. Esto implica identificar las operaciones aritméticas y lógicas que deben ser soportadas y diseñar la ALU para manejar cada una de estas operaciones de manera eficiente.

Diseño de circuitos combinacionales

La ALU está formada principalmente por circuitos combinacionales, que son circuitos digitales sin memoria que realizan operaciones basadas únicamente en las entradas presentes en un momento dado. Es esencial diseñar estos circuitos combinacionales de manera óptima para lograr un rendimiento y velocidad adecuados.

Teorías para el diseño de ALU

Optimización de operaciones aritméticas

Para realizar sumas, restas, multiplicaciones y otras operaciones aritméticas, se deben utilizar circuitos especializados, como sumadores y multiplicadores, que estén optimizados para reducir la latencia y el consumo de recursos.

Manejo de números con signo

Para soportar números con signo, la ALU debe estar diseñada para realizar operaciones de complemento a dos, ya que es la representación más común para números con signo en sistemas digitales.

Teorías para el diseño de ALU

Reducción de latencia y consumo de energía

La latencia y el consumo de energía son consideraciones importantes en el diseño de ALUs para lograr un rendimiento óptimo y un uso eficiente de los recursos.

Soporte para operaciones de desplazamiento

Pueden incluir circuitos para operaciones de desplazamiento, como desplazamiento a la izquierda o a la derecha, para implementar multiplicaciones y divisiones rápidas y otras operaciones.

Teorías para el diseño de ALU

Implementación de detección de desbordamiento

Debe estar diseñada para detectar desbordamientos en operaciones aritméticas y manejarlos adecuadamente.

Unidades de control y decodificación de instrucciones

Debe ser capaz de interpretar las instrucciones del procesador y ejecutar la operación correcta según la instrucción recibida.

Verificación y pruebas

Es esencial llevar a cabo una verificación y pruebas exhaustivas para garantizar que la ALU funcione correctamente en todas las situaciones y cumpla con los requisitos de diseño.

Teorías para el diseño de ALU

El diseño de una ALU es un proceso complejo que involucra una combinación de ingeniería de hardware, lógica digital y conocimientos de arquitectura de computadoras. Se busca crear una ALU que sea eficiente, rápida, confiable y que cumpla con las necesidades específicas del sistema en el que se implementará.

Teoría para el diseño de alu

Magnitud:

se refiere al valor absoluto de un número, es decir, su valor numérico sin considerar el signo. En sistemas digitales, los números se representan utilizando bits, y la magnitud de un número se expresa mediante su valor binario. Por ejemplo, en una ALU de 8 bits, la magnitud del número binario 01101010 es 106, ya que representa el número decimal positivo 106 en magnitud

Teoría para el diseño de alu

Signo:

indica si un número es positivo o negativo. En la representación binaria de números con signo, el bit más significativo (MSB, por sus siglas en inglés) se utiliza como el bit de signo. Si el bit de signo es 0, el número se considera positivo. Si el bit de signo es 1, el número se considera negativo. El resto de los bits en la representación binaria representa la magnitud del número.

Ejemplo de magnitud y signo

En una ALU de 8 bits, el número binario 10011010 representa el número decimal negativo -106, ya que el bit más significativo es 1, lo que indica un número negativo, y los otros bits representan la magnitud 106.

Recordar que en el bit significativo es el que este más a la izquierda

Para operaciones de suma y resta, se deben considerar los desbordamientos y la detección de signo. Para operaciones lógicas, se deben aplicar las operaciones a cada bit correspondiente y tener en cuenta los bits de signo.

Teoría para el diseño de alu

Complementos a uno.

es una técnica de representación de números negativos en binario que se utiliza comúnmente en sistemas digitales y computadoras. Se basa en la inversión de todos los bits de un número binario para obtener su representación en complemento a uno

Teoría para el diseño de alu

Complementos a dos.

es una técnica más común y ampliamente utilizada para representar números negativos en binario en sistemas digitales y computadoras. A diferencia del complemento a uno, el complemento a dos resuelve el problema de tener dos representaciones diferentes para el número 0 (positivo y negativo) y permite realizar operaciones aritméticas más consistentes, como sumas y restas.

Pasos para el uso del complemento a uno

Toma el número binario original.
Invierte (cambia 0 por 1 y 1 por 0) todos los bits del número original.

Ejemplo del complemento a uno

Suponga que se tiene el número binario 01011001, su complemento a uno sería:

Número original:  0 | 1 | 0 | 1 | 1 | 0 | 0 | 1
Complemento a uno: 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0

El bit más significativo (el bit más a la izquierda) se utiliza como el bit de signo. Si el bit más significativo es 0, el número es positivo; si es 1, el número es negativo.

El complemento a uno de un número positivo resulta en un número negativo, mientras que el complemento a uno de un número negativo resulta en un número positivo.

Ejemplo del complemento a uno

Suponga que se tiene el número binario 01100110, su complemento a uno sería:

Número original:  0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
Complemento a uno: 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1

El complemento a uno de 01100110 representa el número decimal negativo -102.

Limitaciones complemento a uno

La presencia de dos representaciones diferentes para el número 0 (positivo y negativo).
El desbordamiento en algunas operaciones.

Para resolver estas limitaciones, se utiliza una técnica más común llamada complemento a dos, que se basa en el complemento a uno con una modificación adicional.

Complemento a uno

def complemento_a_uno(binario):
    complemento = ''
    for bit in binario:
        complemento += '0' if bit == '1' else '1'
    return complemento

def main():
    numero_binario = input("Ingresa el número binario: ")
    complemento = complemento_a_uno(numero_binario)
    print(f"El complemento a uno de {numero_binario} es: {complemento}")

if __name__ == "__main__":
    main()

Actividad de aprendizaje

Ejecuta el script anterior escrito en python y coloca el complemento a uno de los siguientes números decimales:
- 76
- 793
- 693

Pasos para el uso del complemento a dos

Toma el número binario original.
Invierte (cambia 0 por 1 y 1 por 0) todos los bits del número original.
Añade 1 al resultado obtenido en el paso anterior.

Ejemplo de complemento a dos

Si se tiene el número binario 01011001, su complemento a dos sería:

Número original:  0 | 1 | 0 | 1 | 1 | 0 | 0 | 1
Complemento a uno: 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0
Complemento a dos: 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1

El bit más significativo (el bit más a la izquierda) también se utiliza como el bit de signo

Si el bit más significativo es 0, el número es positivo; si es 1, el número es negativo.

El complemento a dos de un número positivo es el mismo número original, y el complemento a dos de un número negativo es su valor absoluto (magnitud) más 1.

Ejemplo de complemento a dos

Si se tiene el número binario 01100110, su complemento a dos sería:

Número original:  0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
Complemento a uno: 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1
Complemento a dos: 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0

Es ampliamente utilizado en sistemas digitales para representar números con signo y realizar operaciones aritméticas y lógicas de manera eficiente y consistente. Es una técnica poderosa y necesaria para el manejo de números negativos en aritmética binaria.

Complemento a dos

def complemento_a_dos(binario):
    # Invertir todos los bits del número original
    complemento_uno = ''.join('1' if bit == '0' else '0' for bit in binario)

    # Sumar 1 al complemento a uno para obtener el complemento a dos
    carry = 1
    complemento_dos = ''
    for bit in reversed(complemento_uno):
        if bit == '1' and carry == 1:
            complemento_dos = '0' + complemento_dos
        elif bit == '0' and carry == 1:
            complemento_dos = '1' + complemento_dos
            carry = 0
        else:
            complemento_dos = bit + complemento_dos

    return complemento_dos

def main():
    numero_binario = input("Ingresa el número binario: ")
    complemento = complemento_a_dos(numero_binario)
    print(f"El complemento a dos de {numero_binario} es: {complemento}")

if __name__ == "__main__":
    main()

Actividad de aprendizaje

Ejecuta el script anterior escrito en python y coloca el complemento a uno de los siguientes números decimales:
- 337
- 663
- 993

Uno

Representación de números negativos
- Se representan invirtiendo (cambiando 0 por 1 y 1 por 0) todos los bits del número positivo correspondiente.
- El bit más significativo se utiliza como el bit de signo

Dos

Representación de números negativos
- Se representan invirtiendo todos los bits del número positivo correspondiente y luego sumando 1 al resultado.
- el bit más significativo se utiliza como el bit de signo.

Diferencia entre complemento

Uno

Operaciones aritméticas
- no permite realizar operaciones aritméticas directamente en los números en su forma de complemento a uno

Dos

Operaciones aritméticas
- permite realizar operaciones aritméticas directamente en los números en su forma de complemento a dos.

Diferencia entre complemento

DISEÑO ALU

Diseñar una unidad aritmética-lógica a nivel de compuertas lógicas.

Previamente saber

Sistemas numéricos y representación binaria: Comprender los sistemas numéricos, especialmente el sistema binario, y cómo representar números, tanto positivos como negativos, utilizando la representación en complemento a dos
Álgebra booleana y compuertas lógicas: Conocer las operaciones básicas de álgebra booleana (AND, OR, NOT) y cómo se implementan estas operaciones utilizando compuertas lógicas (AND, OR, NOT, XOR, y demás).
Circuitos combinacionales: Comprender los conceptos de circuitos combinacionales, que son circuitos digitales sin memoria que realizan operaciones basadas únicamente en las entradas presentes en un momento dado.

Previamente saber

Sumadores y multiplicadores: Conocer el funcionamiento de los sumadores y multiplicadores, que son bloques fundamentales para realizar operaciones aritméticas en la ALU.
Decodificadores y multiplexores: Familiarizarse con los decodificadores y multiplexores, que se utilizan para seleccionar diferentes operaciones y rutas de datos en la ALU.
Máquinas de estado y secuencialidad: Entender los conceptos de máquinas de estado y secuencialidad, ya que algunos diseños de ALU pueden requerir lógica secuencial.
Diseño de circuitos con compuertas lógicas: Saber cómo diseñar circuitos digitales utilizando compuertas lógicas y cómo combinarlas para implementar operaciones y funciones más complejas.

Previamente saber

Diseño de circuitos combinacionales y secuenciales: Tener experiencia en el diseño de circuitos combinacionales y secuenciales utilizando diagramas lógicos, tablas de verdad, mapas de Karnaugh, entre otros.
Conocimiento de herramientas de diseño: Ser capaz de utilizar software de diseño electrónico y simulación de circuitos, como VHDL, Verilog, Logisim, etc., para modelar y verificar el funcionamiento de la ALU.
Comprensión de la arquitectura de una ALU: Entender cómo se integra la ALU en el conjunto del procesador o sistema digital, incluyendo el bus de datos, registros, unidades de control, entre otros.

Pasos para el diseño de una alu

Identificar el tamaño de la ALU: Decida el tamaño de la ALU, es decir, el número de bits que procesará. Por ejemplo, una ALU de 8 bits puede realizar operaciones con números de 8 bits.

Definir las operaciones a implementar: Determine las operaciones aritméticas y lógicas que debe realizar la ALU. Esto incluye operaciones como suma, resta, AND, OR, XOR, entre otras. También considere si la ALU manejará números con signo y, en ese caso, elija la representación adecuada (complemento a dos, por ejemplo).

Pasos para el diseño de una alu

Manejo de números con signo: Si la ALU debe manejar números con signo, implemente la lógica para realizar operaciones en complemento a dos, que es una forma común de representar números con signo en sistemas digitales.

Implementar operaciones lógicas: Utilice compuertas lógicas (AND, OR, XOR) para implementar las operaciones lógicas necesarias.

Diseñar los sumadores y multiplicadores: Para las operaciones aritméticas, diseñe sumadores y multiplicadores de acuerdo con el tamaño de la ALU. Pueden utilizarse sumadores completos, sumadores de acarreo anticipado o sumadores rápidos dependiendo del rendimiento deseado.

Pasos para el diseño de una alu

Integrar en la arquitectura del sistema: Una vez que la ALU ha sido diseñada y probada, integre adecuadamente en la arquitectura del sistema digital o procesador en el que se utilizará.

Conectar las compuertas lógicas: Conecte todas las compuertas lógicas de acuerdo con el diseño del circuito lógico de la ALU.

Decodificar las operaciones: Diseñe un decodificador o un circuito lógico para identificar la operación que se debe realizar en función de las señales de control y los códigos de operación.

Realizar simulaciones y pruebas: Utilice herramientas de simulación o software de diseño electrónico para verificar el funcionamiento de la ALU y realizar pruebas exhaustivas para asegurarse de que funcione correctamente en todos los casos.

Pasos para el diseño de una alu

10.

Conectar las compuertas lógicas: Conecte todas las compuertas lógicas de acuerdo con el diseño del circuito lógico de la ALU.

11.

Integrar en la arquitectura del sistema: Una vez que la ALU ha sido diseñada y probada, integre adecuadamente en la arquitectura del sistema digital o procesador en el que se utilizará.

12.

Ejemplo de diseño de ALU

ALU de 4 bits a nivel de compuertas lógicas que puede realizar las operaciones de suma y resta de números binarios. Se utilizara la representación en complemento a dos para manejar números con signo.

Definición de requerimientos y operaciones:

La ALU debe trabajar con números de 4 bits.
Debe realizar las operaciones de suma y resta.

Especificación de las operaciones:

Suma: Para sumar dos números en complemento a dos, simplemente se aplican las reglas de suma binaria estándar.
Resta: Para restar dos números en complemento a dos, se puede utilizar el mismo circuito que para la suma, pero cambiando el segundo número a su complemento a dos y luego sumándolo al primer número.

Ejemplo de diseño de ALU

Definición de requerimientos y operaciones:

Utilizaremos sumadores completos de 1 bit para construir un sumador de 4 bits.
Utilizaremos compuertas lógicas (AND, OR, XOR) para implementar las operaciones lógicas requeridas.

Implementación del complemento a dos:

Para realizar el complemento a dos de un número binario, se debe invertir cada bit del número y luego sumarle 1.
Implementaremos esto utilizando compuertas NOT para invertir los bits y sumadores completos para agregar 1 al resultado.

Ejemplo de diseño de ALU

       +-------------------+
  A -->|                   |
  B -->|    ALU (4 bits)   |--> Resultado
  S -->|                   |
       +-------------------+

Diagrama de bloques del diseño de la ALU:

Sistemas de memoria

Memoria principales.
Memoria cache.
Memoria externa.

Es una parte esencial de una computadora o sistema informático

Se utiliza para almacenar y recuperar datos e instrucciones de manera temporal o permanente.

Permite que una computadora procese y maneje la información de manera eficiente durante su funcionamiento.

Sistema de memoria

Tipos de memoria

RAM (Memoria de Acceso Aleatorio)

ROM (Memoria de Solo Lectura)

Cache

Virtual

Flash

[A]

[B]

[C]

[D]

[E]

Tipos de memoria

Es la memoria principal de la computadora y se utiliza para almacenar temporalmente datos e instrucciones que están siendo utilizados activamente por el procesador.

Es una memoria no volátil que contiene datos e instrucciones pregrabados que no cambian con el tiempo.

memoria de alta velocidad que se utiliza para almacenar copias temporales de datos e instrucciones utilizados frecuentemente por el procesador.

permite que la computadora ejecute programas que requieren más memoria de la que está físicamente disponible.

La memoria flash es más lenta que la memoria RAM, pero conserva la información incluso cuando se apaga la energía.

[1]

[2]

[3]

[4]

[5]

Actividad de aprendizaje

Relaciona (concepto y definición) los tipos de memorias.

[A]

[B]

[C]

[D]

[E]

[1]

[2]

[3]

[4]

[5]

Microprogramación

Definir los componentes básicos de un controlador microprogramable
Especificar las líneas de interconexión entre el controlador microprogramable y las partes a controlar.
Definir la palabra de control de acuerdo a las especificaciones de un problema dado.
Diseñar controladores microprogramables para ejemplos específicos.

Técnica utilizada en el diseño de computadoras y procesadores para controlar y coordinar las operaciones internas de la unidad central de procesamiento (CPU).

Implementar el conjunto de instrucciones de una arquitectura de procesador utilizando una secuencia de microinstrucciones más simples y a nivel de hardware.

Ejecutan por la unidad de control, traduce las instrucciones de nivel superior a las instrucciones para el hardware.

Solo modificando la secuencia de m.i. almacenadas "memoria de control" o "microprograma".

CPU sea más flexible y fácilmente programable

instrucciones del procesador puede ser cambiado o ampliado sin modificar el hardware en sí

¿qué lenguaje se hace microprogramación?

Microcode (Microcódigo)

VHDL (VHSIC Hardware Description Language)

Verilog

Assembler o Lenguaje Ensamblador Personalizado

Microcode (Microcódigo)

Microprogramación

Lenguaje de descripción de hardware específico para la microprogramación.
Es un lenguaje de bajo nivel que permite definir secuencias de microinstrucciones que controlan la ejecución de las instrucciones de nivel superior en la CPU.
Cada microinstrucción representa una operación elemental que se ejecuta a nivel de hardware.
Los microprogramas se almacenan en una memoria de control especial dentro del microprocesador.

VHDL (VHSIC Hardware Description Language):

Microprogramación

Lenguaje HDL estándar utilizado para describir sistemas digitales.
Utilizado para describir tanto la lógica de control como el hardware digital en un microprocesador.
VHDL es ampliamente utilizado en el diseño de circuitos integrados y sistemas embebidos.

Verilog

Microprogramación

Es un lenguaje HDL comúnmente utilizado en el diseño de hardware.
Usado para describir la lógica de control y el hardware en un microprocesador.
Verilog es ampliamente utilizado en la industria de diseño de circuitos integrados y sistemas embebidos.

Assembler o Lenguaje Ensamblador Personalizado

Microprogramación

Algunas arquitecturas de procesadores utilizan un lenguaje de ensamblador personalizado para la microprogramación.
Estos lenguajes pueden ser específicos para una arquitectura en particular y permiten describir las microinstrucciones y su secuencia de ejecución de manera más directa y específica para el hardware en cuestión.

Microprogramación

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;

entity Adder is
    Port ( A : in STD_LOGIC_VECTOR(3 downto 0);
           B : in STD_LOGIC_VECTOR(3 downto 0);
           Sum : out STD_LOGIC_VECTOR(3 downto 0));
end Adder;

architecture Behavioral of Adder is
begin
    Sum <= A + B;
end Behavioral;

Ejemplo de una suma en VHDL

Microprogramación

module Adder(input [3:0] A, input [3:0] B, output [3:0] Sum);
    assign Sum = A + B;
endmodule

Ejemplo de una suma en Verilog

Microprogramación

.data
.text
    # Inicialización de registros
    li $t0, 5    # Cargar el valor 5 en el registro $t0
    li $t1, 3    # Cargar el valor 3 en el registro $t1

    # Suma de $t0 y $t1
    add $t2, $t0, $t1

    # Finalizar el programa
    li $v0, 10   # Cargar el código de finalización del programa en $v0
    syscall     # Hacer una llamada al sistema para salir del programa

Ejemplo de una suma en lenguaje ensamblador

Actividad de aprendizaje

Visita el sitio www.frexus.dev
Has clic en la sección de slide
Luego pulsa sobre la opción que tiene el nombre de la materia "arq. de computadoras"
Abre la presentación
De los tres códigos anteriores analízalos y reponde lo siguiente:
¿Qué diferencia hay entre cada código?

Microprogramación

Definir los componentes básicos de un controlador microprogramable

Microprogramación

¿controlador microprogramable?

Controlador:

Es un componente o dispositivo que tiene la función de dirigir o coordinar el funcionamiento de otros componentes, dispositivos o sistemas para lograr un objetivo específico.

Los controladores pueden ser hardware, software o una combinación de ambos, dependiendo de la aplicación y el sistema que se esté controlando.

Microprogramación

¿controlador microprogramable?

Controlador microprogramable:

Es un componente de hardware diseñado para controlar y coordinar las operaciones internas de una Unidad Central de Procesamiento (CPU) utilizando la técnica de microprogramación.

Microprogramación

Características y funciones

Controlador

Control y Coordinación

Toma de Decisiones

Interacción con el Entorno

Funcionamiento de otros componentes o sistemas para asegurar que trabajen juntos de manera eficiente y efectiva.

Basadas en reglas predefinidas, entradas del usuario o datos de sensores. Estas decisiones determinan el comportamiento del sistema controlado.

recibir datos o información del entorno a través de sensores y actuar en consecuencia para mantener un estado deseado o responder a cambios externos.

Microprogramación

Características y funciones

Controlador

Implementación de Algoritmos

Retroalimentación (Feedback):

En algunos casos, un controlador implementa algoritmos matemáticos o lógicos para realizar tareas específicas.

Algunos controladores reciben información de retroalimentación (feedback) para ajustar su comportamiento y mejorar su desempeño.

Microprogramación

Ejemplos

Controlador

Controladores de Dispositivos Periféricos

Controladores de Robótica

Son controladores son programas de software que interactúan con los dispositivos periféricos de una computadora, como impresoras, teclados, ratones, etc., para coordinar su funcionamiento y permitir la comunicación entre la computadora y los periféricos.

Son responsables de dirigir los movimientos y operaciones de los robots basándose en datos de sensores y algoritmos de control.

Microprogramación

Ejemplos

Controlador

Controladores de Procesadores (CPU)

Controladores de Sistemas Automatizados

Es responsable de interpretar las instrucciones de máquina y coordinar las operaciones internas de la CPU para ejecutar las instrucciones.

Sistemas de control de tráfico, sistemas de climatización o sistemas de gestión de procesos industriales, el controlador toma decisiones y ajusta las operaciones para mantener condiciones óptimas y responder a cambios en el entorno.

Microprogramación

Componentes

Controlador microprogramable

Son aquellos que forman parte de la estructura interna de la CPU y que están específicamente diseñados para controlar y coordinar las operaciones de la Unidad Central de Procesamiento (CPU) utilizando la técnica de microprogramación.

Estos son fundamentales para la ejecución eficiente de las instrucciones de máquina y para asegurar que las operaciones internas del procesador se realicen correctamente.

Microprogramación

Componentes

Controlador microprogramable

Memoria de Control (ROM)

Contador de Microinstrucciones

Donde se almacena el microprograma.

Es un registro que mantiene el número de la microinstrucción actual que se está ejecutando. A medida que se ejecutan las microinstrucciones en el microprograma, este contador se incrementa secuencialmente para acceder a la siguiente microinstrucción.

Microprogramación

Componentes

Controlador microprogramable

Decodificador de Microinstrucciones

Unidad de Control Secuencial

Circuito lógico que decodifica la microinstrucción actual para determinar las operaciones y los registros que deben ser activados o modificados en cada etapa del ciclo de ejecución de la microinstrucción. Se interpreta el contenido de la microinstrucción y controla las señales de control internas de la CPU.

Circuito lógico que se encarga de secuenciar la ejecución de las microinstrucciones, asegurando que se ejecuten en el orden correcto y coordinando las operaciones de control internas de la CPU.

Microprogramación

Componentes

Controlador microprogramable

Unidad de Control de Instrucciones

Señales de Control y Buses de Control

Responsable de obtener las instrucciones de máquina desde la memoria principal o la caché y decodificarlas para determinar la secuencia de microinstrucciones correspondiente que se debe ejecutar para cada instrucción de máquina.

Las señales de control son señales eléctricas que se utilizan para activar o desactivar diferentes componentes y circuitos de la CPU en cada ciclo de ejecución de la microinstrucción.

Los buses de control son líneas de comunicación que transmiten estas señales de control desde la unidad de control a los diversos componentes de la CPU, permitiendo coordinar y controlar el flujo de datos y operaciones dentro de la CPU.

Microprogramación

Componentes

Controlador microprogramable

Unidad de Control de Instrucciones

Señales de Control y Buses de Control

Las señales de control son señales eléctricas que se utilizan para activar o desactivar diferentes componentes y circuitos de la CPU en cada ciclo de ejecución de la microinstrucción.

Actividad de aprendizaje de alto costo

Una placa arduino
Modulo de bluetooth HC 05
Releevador / relay de 5v
Un protoboard
Un soquet
cable para corriente eléctrica
cables para conectar el arduino, al protoboard.

Microprogramación

Actividad de aprendizaje de alto costo

Una placa arduino (https://articulo.mercadolibre.com.mx/MLM-904241494-uno-r3-smd-tecneu-con-cable-usb-compatible-con-ide-arduino-_JM#position=3&search_layout=stack&type=item&tracking_id=9b078b09-4521-43f8-9f7a-b9e4a0b322dd)
Modulo de bluetooth HC 05 (https://articulo.mercadolibre.com.mx/MLM-1466539662-modulo-bluetooth-hc05-arduino-pic-hc-05-hc-06-_JM#position=37&search_layout=stack&type=item&tracking_id=a06ece5c-7622-478b-a3e0-e39369eef4f3)

Microprogramación

Actividad de aprendizaje de alto costo

Releevador / relay de 5v (https://articulo.mercadolibre.com.mx/MLM-657068029-modulo-relevador-relay-1-canal-5v-_JM#position=51&search_layout=grid&type=item&tracking_id=8d94a80c-b70c-4850-91bd-3b7b66a35d49)
Un protoboard (https://articulo.mercadolibre.com.mx/MLM-705443986-protoboard-830-puntos-mb-102-_JM#position=3&search_layout=stack&type=item&tracking_id=3d95afeb-25cc-463c-b2a7-2e4dcb4883b6)

Microprogramación

Actividad de aprendizaje de alto costo

Un socket (https://articulo.mercadolibre.com.mx/MLM-695399479-portalampara-de-porcelana-4-12-circular-volteck-46524-_JM#position=28&search_layout=stack&type=item&tracking_id=9ea4df36-0b14-454d-ae81-342776856e92)
cable para corriente eléctrica
cables dupont hembra-macho para conectar el arduino, al protoboard. (https://articulo.mercadolibre.com.mx/MLM-931045703-120-cables-jumpers-dupont-h-h-m-m-h-m-30cm-para-protoboard-_JM?attributes=VGlwbyBkZSBjb25lY3Rvcg%3D%3D%3ATWFjaG8tTWFjaG8%3D&quantity=1)

Microprogramación

Actividad de aprendizaje de alto costo

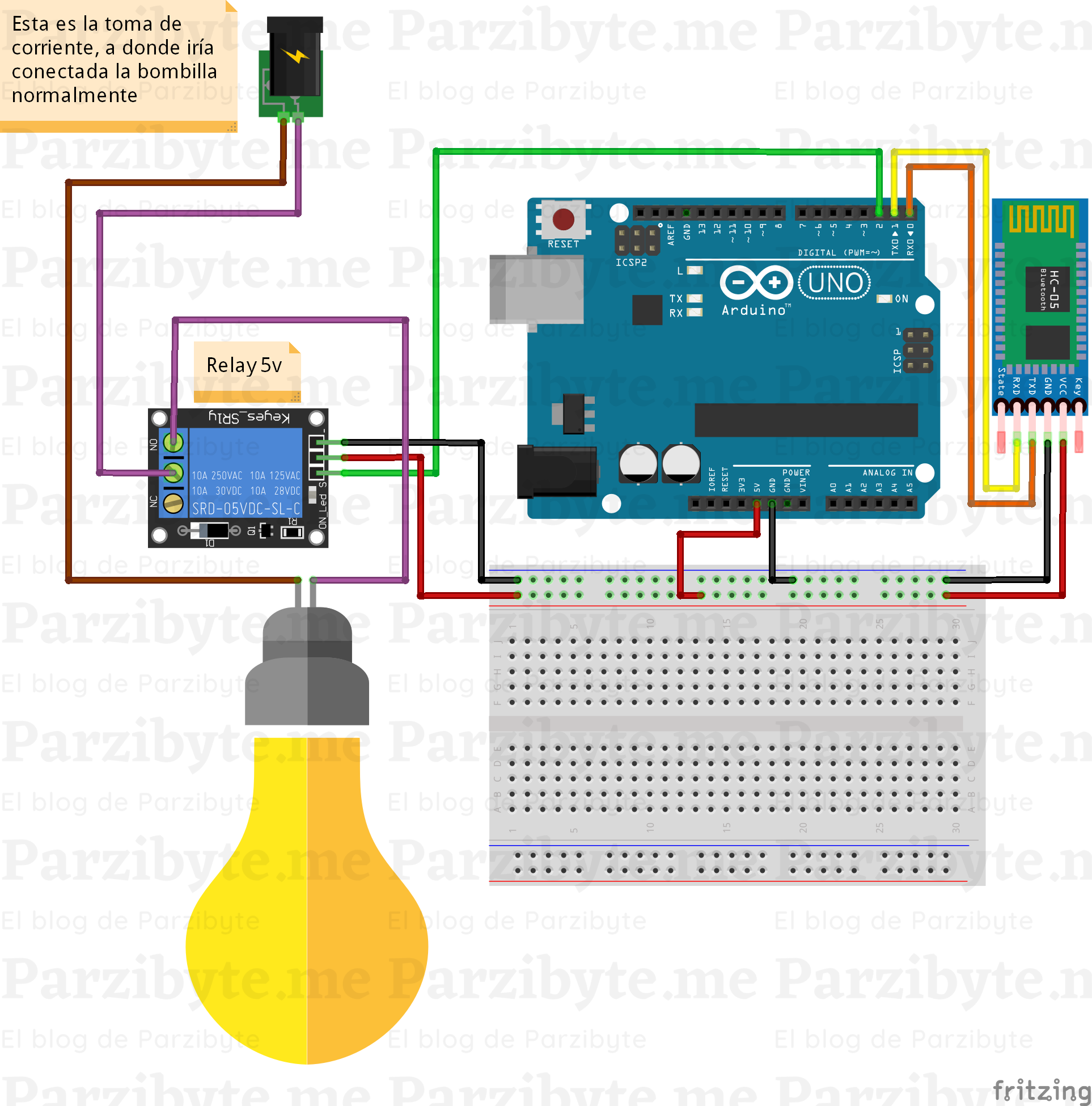
Microprogramación

Actividad de aprendizaje de alto costo

/*https://parzibyte.me/blog*/
#include <Arduino.h>
#define ACCION_ENCENDER 97 // La letra a
#define ACCION_APAGAR 98   // La letra b
#define LED_FOCO_HABITACION 2

void setup()
{
  Serial.begin(9600);
  pinMode(LED_FOCO_HABITACION, OUTPUT);
}
void loop()
{
  if (Serial.available())
  {
    int accion = Serial.read();
    if (accion == ACCION_ENCENDER)
    {
      digitalWrite(LED_FOCO_HABITACION, HIGH);
    }
    else if (accion == ACCION_APAGAR)
    {
      digitalWrite(LED_FOCO_HABITACION, LOW);
    }
  }
}

Microprogramación

Actividad de aprendizaje de alto costo

Referencias:

https://parzibyte.me/blog/2020/12/12/controlar-bombilla-arduino-bluetooth-telefono-movil/

Microprogramación

Especificar las líneas de interconexión entre el controlador microprogramable y las partes a controlar

Microprogramación

¿Qué pines de la placa Arduino están conectados al módulo Bluetooth para la recepción de comandos?
¿Cuáles son las conexiones del módulo Bluetooth al protoboard y al Arduino para permitir la comunicación?
Describe cómo se realiza la conexión entre el relé y el foco para controlar su encendido y apagado.
¿Qué precauciones se deben tener en cuenta al conectar el módulo Bluetooth y el relé a la corriente eléctrica?

Definir la palabra de control de acuerdo a las especificaciones de un problema dado.

Microprogramación

¿Qué es la "palabra de control" en el contexto de la actividad de aprendizaje de alto costo?
Define los comandos específicos que se utiliza para encender y apagar el foco a través del módulo Bluetooth.
¿Cómo se interpretarán los comandos recibidos por el Arduino para activar o desactivar el releevador?
Describe cómo se podría mejorar la "palabra de control" para incluir otros comandos o funcionalidades adicionales.

Microprogramación

Diseñar controladores microprogramables para ejemplos específicos.

Microprogramación

Explica cómo se programa el Arduino para recibir comandos a través del módulo Bluetooth.
¿Cómo se implementa la lógica de control en el Arduino para encender o apagar el relé según los comandos recibidos?
Si quisieras agregar una función de temporizador para apagar automáticamente el foco después de un tiempo determinado, ¿cómo lo harías en el código?
Describe otro ejemplo específico de controlador microprogramable que podrías diseñar utilizando una placa Arduino y otros componentes.

Microprogramación

Diseño de una computadora básica

Integrar los conocimientos diseñando una computadora básica.
Diseñar la unidad de control de la computadora básica con el método de microprogramación.

Conceptos previos

Unidad Central de Procesamiento (CPU)

Diseño de una computadora básica

Comprender la función y organización de la CPU, que incluye la Unidad de Control (UC) para gestionar el flujo de instrucciones y la Unidad Aritmético-Lógica (UAL) para realizar operaciones aritméticas y lógicas.

Conceptos previos

Diseño de una computadora básica

Arquitectura Von Neumann

Es una base común para la mayoría de las computadoras actuales y se caracteriza por la existencia de una memoria compartida que almacena tanto datos como programas.

Conceptos previos

Diseño de una computadora básica

Arquitectura Von Neumann

Conceptos previos

Diseño de una computadora básica

Memoria Principal

Entender la función y la organización de la memoria principal, que almacena datos y programas en celdas de memoria direccionables y accesibles aleatoriamente.

Conceptos previos

Diseño de una computadora básica

Instrucciones y Lenguaje de Máquina:

Conocer el concepto de instrucciones y el lenguaje de máquina, que son representaciones binarias que la CPU puede entender y ejecutar.

Buses de Datos, Direcciones y Control

Comprender los buses de datos, direcciones y control que permiten la comunicación entre la CPU, la memoria y los dispositivos de E/S.

Unidad de Entrada/Salida (E/S)

Entender cómo la CPU se comunica con dispositivos de entrada y salida, como teclados, monitores, impresoras y dispositivos de almacenamiento.

Conceptos previos

Diseño de una computadora básica

Reloj de Sistema

Conocer el concepto de un reloj de sistema que proporciona señales de sincronización para coordinar las operaciones de la computadora.

Circuitos Lógicos y Combinacionales

Comprender los conceptos de circuitos lógicos y combinacionales, que son la base para la implementación de la lógica digital en la CPU.

Programación de Hardware

Aprender lenguajes de descripción de hardware, como VHDL o Verilog, para describir la lógica y funcionalidad de la computadora en un nivel de abstracción más alto.

Conceptos previos

Diseño de una computadora básica

Síntesis y Implementación en FPGA (Field-Programmable Gate Array)

Después de la simulación y corrección de errores, los estudiantes deben llevar a cabo la síntesis y la implementación del diseño en una FPGA real. Pueden utilizar una placa de desarrollo FPGA que contenga suficientes recursos para implementar el diseño.

Dispositivo semiconductor que se utiliza en electrónica digital y diseño de hardware.
Placa de circuito integrado que contiene una matriz de bloques lógicos programables y conexiones configurables.
La característica principal de las FPGAs es que se pueden configurar o programar después de la fabricación para implementar una amplia variedad de funciones y lógica digital.

Conceptos previos

Diseño de una computadora básica

Pruebas y Depuración

Probar la computadora básica en la FPGA y depurar cualquier problema que surja durante las pruebas. Deben asegurarse de que la computadora pueda ejecutar correctamente las operaciones y realizar cálculos básicos.

Conceptos generales sobre arquitecturas computacionales.

Evolución de las arquitecturas de computadoras.
Máquinas cisc.
Máquinas risc.
Comparación cisc vs. risc.
Arquitecturas paralelas.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura de Von Neumann

Es un modelo de arquitectura computacional que se basa en la idea de almacenar tanto los datos como las instrucciones de programa en la memoria principal. La unidad central de procesamiento (CPU) realiza la lectura de instrucciones y datos desde la memoria y ejecuta las operaciones secuencialmente.

CPU (Central Processing Unit)

Es la parte central de un sistema computacional. La CPU ejecuta instrucciones de programa, realiza cálculos y controla las operaciones del sistema. Está compuesta por la Unidad de Control (UC) y la Unidad Aritmético-Lógica (UAL).

Concepto Arq. computacional.

Conceptos Generales

Memoria Principal

Es el espacio de almacenamiento principal del sistema, donde se guardan los programas y datos que la CPU necesita para operar. En una arquitectura de Von Neumann, tanto las instrucciones como los datos se almacenan en la misma memoria.

Buses

Son canales de comunicación que permiten el flujo de datos e instrucciones entre la CPU, la memoria y otros componentes del sistema, como dispositivos de entrada/salida.

Concepto Arq. computacional.

Conceptos Generales

Instrucciones

Son comandos que la CPU puede ejecutar. Cada instrucción realiza una operación específica, como sumar dos números, leer datos de memoria, o tomar decisiones condicionales.

Ciclo de Instrucción

Es el proceso por el cual la CPU busca, decodifica, ejecuta y almacena una instrucción de programa en la memoria. Consiste en una secuencia de pasos que la CPU sigue para procesar una instrucción.

Concepto Arq. computacional.

Conceptos Generales

Pipeline

Es una técnica que se utiliza para aumentar el rendimiento de la CPU al dividir el ciclo de instrucción en varias etapas, de modo que múltiples instrucciones se pueden ejecutar simultáneamente.

Memoria Caché

Es una memoria de alta velocidad y pequeña capacidad que se encuentra más cerca de la CPU que la memoria principal. La memoria caché se utiliza para almacenar copias de datos e instrucciones que la CPU utiliza con frecuencia, lo que acelera el acceso a esos datos e instrucciones.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard

Es un tipo de arquitectura que utiliza memorias separadas para almacenar las instrucciones y los datos. Esto permite que la CPU acceda a instrucciones y datos al mismo tiempo, mejorando el rendimiento.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Ventajas

Mayor rendimiento: Una de las principales ventajas de la arquitectura Harvard es su mayor rendimiento en comparación con la arquitectura de Von Neumann. Al tener memorias separadas para instrucciones y datos, la CPU puede acceder simultáneamente a instrucciones y datos en dos buses distintos, lo que permite una ejecución más rápida y eficiente de las instrucciones.
Menos cuellos de botella: Al tener buses separados para instrucciones y datos, la arquitectura Harvard reduce la posibilidad de cuellos de botella en el acceso a la memoria. En la arquitectura de Von Neumann, el acceso a instrucciones y datos se realiza a través del mismo bus, lo que puede ocasionar conflictos y retrasos.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Ventajas

Mejor paralelismo: La arquitectura Harvard permite un mayor grado de paralelismo en la ejecución de instrucciones. Mientras que en la arquitectura de Von Neumann, la CPU debe esperar a que se complete el acceso a la memoria para obtener una instrucción o un dato, en la arquitectura Harvard, la CPU puede acceder a instrucciones y datos al mismo tiempo, lo que mejora el paralelismo y el rendimiento.
Menor latencia de acceso a instrucciones: La separación de las memorias de instrucciones y datos en la arquitectura Harvard permite una menor latencia de acceso a las instrucciones. La CPU puede acceder directamente a la memoria de instrucciones sin esperar a que se complete el acceso a la memoria de datos.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Ventajas

Eficiencia energética: Debido a su mayor eficiencia en el acceso a instrucciones y datos, la arquitectura Harvard puede ser más eficiente energéticamente en ciertos escenarios de uso, ya que puede minimizar el consumo de energía asociado con el acceso a la memoria.
Aplicaciones específicas: La arquitectura Harvard se utiliza comúnmente en sistemas embebidos y aplicaciones específicas donde se requiere un alto rendimiento y un acceso rápido a las instrucciones y datos, como en sistemas de control en tiempo real, procesamiento de señales digitales (DSP) y sistemas de comunicación.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Desventajas

Mayor complejidad del hardware: La arquitectura Harvard requiere la implementación de buses separados para instrucciones y datos, lo que puede aumentar la complejidad del diseño del hardware. Esto puede resultar en un mayor número de componentes y conexiones, lo que a su vez puede aumentar los costos y la dificultad en la fabricación y mantenimiento de los sistemas basados en esta arquitectura.
Mayor consumo de espacio: Debido a la necesidad de tener memorias separadas para instrucciones y datos, la arquitectura Harvard puede requerir más espacio físico en el chip y en el sistema en comparación con la arquitectura de Von Neumann, donde se utiliza una memoria compartida para instrucciones y datos.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Desventajas

Mayor consumo de energía: Si bien la arquitectura Harvard puede ser más eficiente energéticamente en ciertos escenarios, también puede requerir un mayor consumo de energía debido a la necesidad de mantener y acceder a dos buses separados para instrucciones y datos.
Limitaciones en programas complejos: La arquitectura Harvard puede tener limitaciones en la ejecución de programas complejos que requieren un alto grado de interacción entre instrucciones y datos. En tales casos, el uso de memorias separadas puede generar cuellos de botella y dificultar la ejecución eficiente del programa.

Concepto Arq. computacional.

Conceptos Generales

Arquitectura Harvard - Desventajas

Mayores costos de desarrollo: La mayor complejidad del diseño de hardware y la necesidad de componentes adicionales pueden aumentar los costos de desarrollo y fabricación de sistemas basados en la arquitectura Harvard.
Menor flexibilidad en algunas aplicaciones: La arquitectura Harvard está diseñada para aplicaciones específicas que requieren un alto rendimiento y un acceso rápido a las instrucciones y datos. Sin embargo, en ciertos casos donde se requiere flexibilidad y adaptabilidad, la arquitectura Harvard puede no ser la opción más adecuada.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Primeras computadoras mecánicas

Finales del siglo XIX y principios del siglo XX,

Surgieron las primeras computadoras mecánicas, como la máquina analítica de Charles Babbage y la máquina tabuladora de Herman Hollerith. Estas máquinas utilizaban engranajes y mecanismos para realizar cálculos y procesar datos.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Computadoras de tubos de vacío

Década de 1940

Utilizaban tubos de vacío como componentes electrónicos para realizar cálculos y procesar datos. Ejemplos famosos incluyen ENIAC y UNIVAC.

Décadas de 1930 y 1940,

Computadoras Electromecánicas

Máquinas de relés y los equipos de tarjetas perforadas. Estos sistemas utilizaban relés y tarjetas perforadas para realizar cálculos y procesar datos.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Microprocesadores y computadoras personales

Década de 1970

Los microprocesadores, integraban múltiples funciones de una CPU en un solo chip. Permitió la creación de las primeras computadoras personales (PC) y marcó el inicio de la era de la computación personal.

Fines de la década de 1950 y principios de la década de 1960

Computadoras de transistores

Transistores reemplazaron a los tubos de vacío. Eran más pequeñas, rápidas y confiables que sus predecesoras.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Supercomputadoras y paralelismo

Las supercomputadoras, que utilizan múltiples procesadores en paralelo, se desarrollaron para resolver problemas científicos y técnicos complejos. El paralelismo se volvió cada vez más importante para mejorar el rendimiento en aplicaciones exigentes.

Principios de 1965 hasta finales del 2000

Computadora de 32 y 64 bits

Las computadoras evolucionaron para usar palabras de datos de mayor tamaño, como 32 bits y 64 bits. Permitió un mayor rendimiento y capacidad de memoria.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Supercomputadoras y paralelismo

Principios de 1965 hasta finales del 2000

Computación móvil y dispositivos portátiles

Se desarrollaron computadoras portátiles y dispositivos móviles, como teléfonos inteligentes y tabletas, que permiten la computación en movimiento.

Concepto Arq. computacional.

Evolución de las arq. de computadoras

Computación cuántica

Campo emergente que utiliza principios de la mecánica cuántica para realizar cálculos a una escala y velocidad que van más allá de las capacidades de las computadoras clásicas.

Principios de 1965 hasta la fecha

Computación en la nube

Permite el acceso a recursos informáticos a través de internet, lo que ha revolucionado la forma en que se proporcionan y utilizan los servicios de computación.

Concepto Arq. computacional.

Máquinas cisc

CISC (Complex Instruction Set Computer) es un tipo de arquitectura de computadora que se caracteriza por tener un conjunto de instrucciones complejas y variadas.
En una máquina CISC, cada instrucción puede realizar múltiples operaciones y acceder a múltiples operandos en una sola instrucción.

Concepto Arq. computacional.

Máquinas cisc - Características

Las instrucciones de una máquina CISC pueden ser muy detalladas y llevar a cabo múltiples operaciones en una sola instrucción.

Estas instrucciones pueden incluir operaciones aritméticas, lógicas, de carga y almacenamiento de datos, así como operaciones de salto y llamadas a subrutinas.

Conjunto de instrucciones complejas:

Concepto Arq. computacional.

Máquinas cisc - Características

Las máquinas CISC suelen admitir varios modos de direccionamiento, lo que permite acceder a los operandos de diferentes formas, como direccionamiento inmediato, directo, indirecto y relativo.

Modos de direccionamiento:

En una máquina CISC, las instrucciones pueden tener longitudes variables, lo que significa que algunas instrucciones pueden requerir más bytes para representarlas que otras.

Instrucciones de longitud variable

Concepto Arq. computacional.

Máquinas cisc - Características

Debido a la complejidad de las instrucciones, las máquinas CISC pueden requerir más memoria para almacenar el código de programa y las instrucciones.

Uso intensivo de memoria

Procesador x86 de Intel y AMD, que es ampliamente utilizado en computadoras personales
Procesador Motorola 68000, que fue utilizado en computadoras Apple Macintosh más antiguas.

Ejemplos

Concepto Arq. computacional.

Máquinas cisc - arq.

Concepto Arq. computacional.

Máquinas risc

Una máquina RISC (Reduced Instruction Set Computer) es un tipo de arquitectura de computadora que se caracteriza por tener un conjunto de instrucciones reducido y simple. En una máquina RISC, cada instrucción realiza una operación básica y sencilla en una sola instrucción, lo que facilita la ejecución rápida de las instrucciones.

Concepto Arq. computacional.

Máquinas risc - Características

El conjunto de instrucciones en una máquina RISC es más pequeño en comparación con una máquina CISC (Complex Instruction Set Computer). Cada instrucción se diseña para ser ejecutada en un solo ciclo de reloj y realizar operaciones simples, como cargar, almacenar, sumar, restar y operaciones lógicas básicas.

Conjunto de instrucciones reducido

Concepto Arq. computacional.

Máquinas risc - Características

Las máquinas RISC tienden a tener modos de direccionamiento más simples y directos, lo que ayuda a reducir la complejidad del hardware y acelera la ejecución de las instrucciones.

Modos de direccionamiento simples

En una máquina RISC, las instrucciones suelen tener una longitud fija, lo que facilita la decodificación y la ejecución más rápida de las instrucciones.

Longitud de instrucción fija

Concepto Arq. computacional.

Máquinas risc - Características

Las máquinas RISC suelen utilizar un conjunto de registros de propósito general y favorecen el almacenamiento y procesamiento de datos en registros en lugar de la memoria, lo que ayuda a mejorar el rendimiento.

Uso intensivo de registros

Surgieron en respuesta a la complejidad de las máquinas CISC y se enfocaron en la eficiencia y el rendimiento optimizado para ciertas aplicaciones. Ejemplos de arquitecturas RISC incluyen ARM, MIPS y RISC-V.

Concepto Arq. computacional.

Máquinas risc - Características

Uso intensivo de registros

Concepto Arq. computacional.

Máquinas risc - Ejemplos

Ampliamente utilizada en dispositivos móviles, como teléfonos inteligentes y tabletas, así como en sistemas embebidos, microcontroladores y otros dispositivos de bajo consumo de energía. ARM es conocida por su eficiencia energética y su flexibilidad en términos de diseño y configuración.

ARM (Advanced RISC Machines):

Usada en una variedad de aplicaciones, desde estaciones de trabajo y servidores hasta dispositivos embebidos y sistemas integrados. MIPS ha sido ampliamente utilizado en la industria y la academia debido a su diseño limpio y su enfoque en la eficiencia de ejecución de instrucciones.

MIPS (Microprocessor without Interlocked Pipeline Stages):

Concepto Arq. computacional.

Máquinas risc - Ejemplos

Es una arquitectura RISC de código abierto, de las más recientes en el campo. Su diseño modular permite a los diseñadores adaptar la arquitectura a las necesidades específicas de su aplicación.

RISC-V: RISC-V

Utilizada en sistemas Unix y estaciones de trabajo. A lo largo de los años, ha sido diseñada para escalabilidad y rendimiento en sistemas multiprocesador.

SPARC (Scalable Processor Architecture)

Concepto Arq. computacional.

Máquinas risc - Ejemplos

Utilizada en computadoras personales y sistemas embebidos. Desarrollada conjuntamente por IBM, Motorola y Apple, y ha sido conocida por su rendimiento en aplicaciones de alto rendimiento y multimedia.

PowerPC

Desarrollada por DEC (Digital Equipment Corporation), se destacó por su rendimiento en sistemas de alto rendimiento y servidores.

Alpha

Concepto Arq. computacional.

Máquinas risc - Arq.

Concepto Arq. computacional.

Risc vs Cisc

Conjunto de instrucciones

RISC: Las máquinas RISC tienen un conjunto de instrucciones reducido y simple, donde cada instrucción realiza una operación básica en una sola etapa de ejecución. Las instrucciones son generalmente de longitud fija y realizan tareas específicas.

CISC: Las máquinas CISC tienen un conjunto de instrucciones complejo y variado, donde cada instrucción puede realizar múltiples operaciones y acceder a múltiples operandos en una sola instrucción. Las instrucciones pueden tener longitudes variables.

Concepto Arq. computacional.

Risc vs Cisc

Complejidad de instrucciones

RISC: Las instrucciones en una máquina RISC son más simples y específicas, lo que facilita la implementación del hardware y la ejecución rápida de las instrucciones.

CISC: Las instrucciones en una máquina CISC pueden ser más complejas y detalladas, lo que puede requerir más etapas de ejecución y hardware más complejo para decodificar y ejecutar las instrucciones.

Concepto Arq. computacional.

Risc vs Cisc

Modos de direccionamiento

RISC: Las máquinas RISC generalmente tienen modos de direccionamiento más simples y directos, como direccionamiento inmediato, directo e indirecto.

CISC: Las máquinas CISC pueden tener modos de direccionamiento más variados y complejos, lo que les permite acceder a operandos de diversas maneras.

Concepto Arq. computacional.

Risc vs Cisc

Uso de registros

RISC: Las máquinas RISC tienden a utilizar un conjunto de registros de propósito general y favorecen el almacenamiento y procesamiento de datos en registros en lugar de la memoria.

CISC: Las máquinas CISC pueden hacer un uso más intensivo de la memoria, y algunas instrucciones pueden operar directamente en la memoria.

Concepto Arq. computacional.

Risc vs Cisc

Arquitectura de hardware

RISC: Las máquinas RISC son más fáciles de diseñar y tienen un hardware más simple, lo que las hace más eficientes en términos de consumo de energía y rendimiento.

CISC: Las máquinas CISC pueden requerir hardware más complejo y son más propensas a tener ciclos de reloj más largos.

Concepto Arq. computacional.

Risc vs Cisc

Rendimiento y optimización

RISC:Las máquinas RISC son más adecuadas para aplicaciones que requieren un rendimiento consistente y predecible, como cálculos científicos, sistemas embebidos y dispositivos móviles.

CISC: Las máquinas CISC pueden ser más adecuadas para aplicaciones que requieren una amplia variedad de operaciones complejas en una sola instrucción, como aplicaciones empresariales y de servidor.

Concepto Arq. computacional.

Arq. paralela

Conocida como computación paralela, es un enfoque en el diseño de sistemas informáticos que utiliza múltiples unidades de procesamiento trabajando en conjunto para realizar tareas computacionales.

El objetivo principal de la arquitectura paralela es aumentar el rendimiento y la velocidad de procesamiento al dividir una tarea en subproblemas más pequeños y resolverlos simultáneamente en paralelo.

En lugar de depender de un solo procesador para ejecutar una secuencia de instrucciones en orden secuencial, la arquitectura paralela utiliza múltiples procesadores o núcleos de procesamiento para trabajar en paralelo en tareas independientes o partes de una tarea más grande.

Concepto Arq. computacional.

Arq. paralela - tipos

Este enfoque busca aprovechar la capacidad de superposición de instrucciones para mejorar el rendimiento. Los procesadores modernos utilizan técnicas como la ejecución fuera de orden (Out-of-Order Execution) y el procesamiento de instrucciones en paralelo (Superscalar) para lograr un mayor rendimiento a nivel de instrucción.

Paralelismo a nivel de instrucciones (ILP, Instruction-Level Parallelism)

Concepto Arq. computacional.

Arq. paralela - tipos

Este enfoque divide una tarea en subproblemas más pequeños y los distribuye entre múltiples procesadores o núcleos para que puedan ejecutarse en paralelo. Esto se utiliza comúnmente en sistemas multiprocesador o en arquitecturas multinúcleo.

Paralelismo a nivel de tareas (TLP, Task-Level Parallelism)

Concepto Arq. computacional.

Arq. paralela - usada

Aplicaciones y escenarios donde se requiere un alto rendimiento y velocidad de procesamiento, como en supercomputadoras para realizar cálculos científicos intensivos, en servidores para soportar múltiples clientes simultáneos, y en sistemas de inteligencia artificial y aprendizaje profundo para acelerar el procesamiento de grandes conjuntos de datos.

Concepto Arq. computacional.

Arq. paralela - usada

Aplicaciones y escenarios donde se requiere un alto rendimiento y velocidad de procesamiento, como en supercomputadoras para realizar cálculos científicos intensivos, en servidores para soportar múltiples clientes simultáneos, y en sistemas de inteligencia artificial y aprendizaje profundo para acelerar el procesamiento de grandes conjuntos de datos.

Fin

Arq. de Computadoras - temas

By Alfredo de Jesús Gutiérrez Gómez

Arq. de Computadoras - temas

Esta presentación contiene todo el desarrollo temático de la materia en cuestion.

Alfredo de Jesús Gutiérrez Gómez

frexus.dev