2015-02
Recursion and Mod
同餘
a\%M=a',\ b\%M=b'
a%M=a′, b%M=b′
(a+b)\%M=(a'+b')\%M
(a+b)%M=(a′+b′)%M
(a*b)\%M\ =(a'*b')\%M
(a∗b)%M =(a′∗b′)%M
題目敘述
Definition:
a_{1} = 1
a1=1
a_{n} = 3*a_{n-1} + 4
an=3∗an−1+4
N<2^{63},MOD=10^9+9
N<263,MOD=109+9
解法一
就照著遞迴式做
時間複雜度:
O(N)=O(2^{63})=TLE
O(N)=O(263)=TLE
0.4
Hint:
需要一個迴圈
解法二
先觀察數列
a_{1}=1,a_{2}=7,a_{3}=25,a_{4}=79
a1=1,a2=7,a3=25,a4=79
似乎有甚麼規律
解法二
似乎?
a_{n}=3^{n}-2
an=3n−2
解法二
按照定義展開
a_{1}=1
a1=1
a_{2}=3*a_{1}+4
a2=3∗a1+4
a_{3}=3*a_{2}+4=3*(3*a_{1}+4)+1
a3=3∗a2+4=3∗(3∗a1+4)+1
解法二
a_{4}=3*a_{3}+4
a4=3∗a3+4
=3*(3*a_{2}+4)+4
=3∗(3∗a2+4)+4
=3*(3*(3*a_{1}+4)+4)+4
=3∗(3∗(3∗a1+4)+4)+4
=3^{3}*a_{1}+4*(3^{2}+3^{1}+3^{0})
=33∗a1+4∗(32+31+30)
=3^{3}+4*(3^3-1)/(3-1)
=33+4∗(33−1)/(3−1)
=3^{3}+2*3^{3}-2
=33+2∗33−2
=3^{4}-2
=34−2
解法二
再用數學歸納法仔細證明
a_{n}=3^{n}-2
an=3n−2
n=1 =>a_{1}=3^{1}-2=1
n=1=>a1=31−2=1
n=k+1=>a_{k+1}=3*a_{k}+4
n=k+1=>ak+1=3∗ak+4
=3*(3^{k}-2)+4
=3∗(3k−2)+4
=3^{k+1}-2
=3k+1−2
解法二
因此我們得知
a^{n}=3^n-2
an=3n−2
時間複雜度:
O(N)=O(2^{63})=TLE
O(N)=O(263)=TLE
0.4
Hint:
一個迴圈算3的冪次
解法三
把遞迴式變成一般式
目標: 如何快速求得 ???
3^{n}
3n
快速冪
Fast Exponential Algorithm
快速冪
a^{n}={(a^{n/2})}^{2}
an=(an/2)2
={(a^{[n/2]})}^{2}*a
=(a[n/2])2∗a
if n is even
if n is odd
快速冪
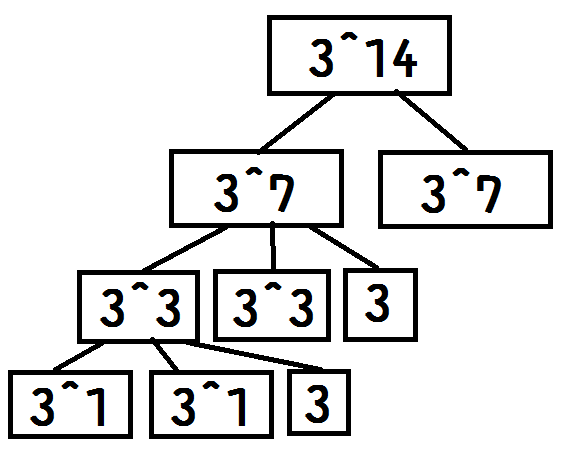
3^{14}=(3^{7})^{2}
314=(37)2
3^{7}=(3^{3})^{2}*3
37=(33)2∗3
3^{3}=(3^{1})^{2}*3
33=(31)2∗3
解法三
時間複雜度:
O(lgN)=O(lg2^{63})=O(63)
O(lgN)=O(lg263)=O(63)
AC
Hint:
用一個遞迴實現上述的遞迴式
a^{n}={(a^{n/2})}^{2}
an=(an/2)2
={(a^{[n/2]})}^{2}*a
=(a[n/2])2∗a
if n is even
if n is odd
Copy of GPE 5/18
By allenwhale
Copy of GPE 5/18
- 750



