時間複雜度

TIME COMPLEXITY

假設我們的電腦每秒可以做10億次運算

可是怎麼知道是哪個數量級?

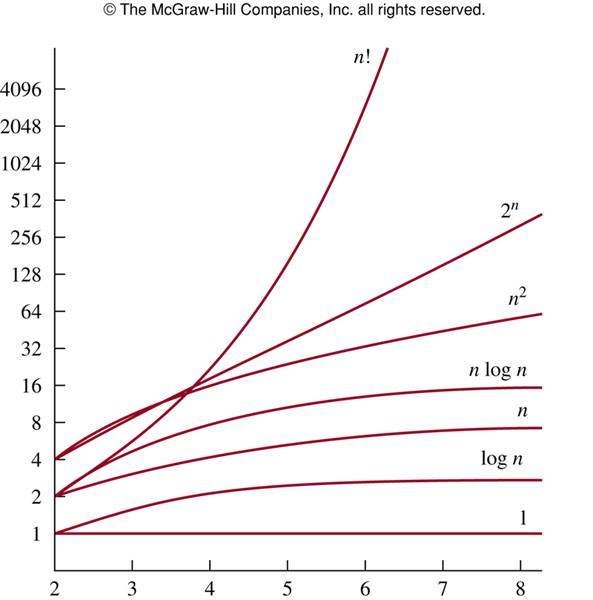
怎麼估計一個程式的執行時間

x^{2}+x+3\ \ v.s.\ \ 2x^{2}-3x+8\ ???
x​2​​+x+3  v.s.  2x​2​​−3x+8 ???
n!\ \ v.s.\ \ 2^{n}\ ???
n!  v.s.  2​n​​ ???

到底怎麼定義???

O
O
\Omega
Ω
\Theta
Θ

Big O

Omega

Theta

O(g(n)),\Omega(g(n)),\Theta(g(n))
O(g(n)),Ω(g(n)),Θ(g(n))

可以想像成集合

Theta

\Theta
Θ
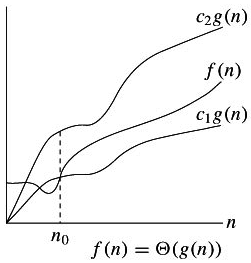
f(n)=\Theta(g(n))
f(n)=Θ(g(n))
c_{2}g(n)\ge f(n)\ (n\ge n_{0})
c​2​​g(n)≥f(n) (n≥n​0​​)
c_{1}g(n)\le f(n)\ (n\ge n_{0})
c​1​​g(n)≤f(n) (n≥n​0​​)
ex:f(n)=2n^{2}+n
ex:f(n)=2n​2​​+n
f(n)=\Theta(n^{2})
f(n)=Θ(n​2​​)

Theta

\Theta
Θ
f(n)=2n^{2}+n=\Theta(n^{2})
f(n)=2n​2​​+n=Θ(n​2​​)
c_{1}=3,\ 3n^{2}\ge 2n^{2}+n\ (n\ge 1)
c​1​​=3, 3n​2​​≥2n​2​​+n (n≥1)
c_{2}=1,\ n^{2}\ \ \le 2n^{2}+n\ (n\ge 1)
c​2​​=1, n​2​​  ≤2n​2​​+n (n≥1)

Theta Example

\Theta
Θ
int A[10]={0,1,9,2,8,3,7,4,6,5};
int N=10;
for(int i=0;i<N;i++){ //1
    for(int j=0;j<N-1;j++){//2
        if(A[i]>A[j])swap(A[i],A[j]);//3
    }//4
}//5

Bubble Sort

Line 1~5: 執行N次=>

Line 2~4: 執行N-1次=>

Line 3: 花費時間=1 =>

\Theta(N)
Θ(N)
\Theta(N-1)=\Theta(N)
Θ(N−1)=Θ(N)
\Theta(1)
Θ(1)

總時間複雜度:

\Theta(N)*\Theta(N)*\Theta(1)
Θ(N)∗Θ(N)∗Θ(1)
=\Theta(N^{2})
=Θ(N​2​​)
=\Theta(N^{2})
=Θ(N​2​​)

Big O /    Omega

O
O
\Omega
Ω
O(g(n))
O(g(n))
\Omega(g(n))
Ω(g(n))

Confusion

f(n)=n^{2}+n
f(n)=n​2​​+n
f(n)=O(n^2)
f(n)=O(n​2​​)
f(n)=O(n^3)
f(n)=O(n​3​​)

為甚麼      有兩個答案?

f(n)
f(n)

Confusion

沒錯，都是答案

但是需要準確的答案

f(n)=n^{2}+n=O(n^{2})\ !!!!!
f(n)=n​2​​+n=O(n​2​​) !!!!!

Example

//binary search
int A[]={0,1,2,13,14,15,26,27,28,39};
int N=10;
int l=0,r=N-1,find=26,ans=-1;
while(l<=r){//1
    int mid=(l+r)//2;
    if(A[mid]==find)ans=mid;//3
    else if(A[mid]>find)r=mid-1;//4
    else if(A[mid]<find)l=mid+1;//5
}//6
O(lgN)
O(lgN)

Example

//find the max element
int A[]={1,0,2,9,3,8,4,7,5,6};
int N=10,mx=-100000000;
for(int i=0;i<N;i++){//1
    mx=max(mx,A[i]);//2
}//3
O(N)
O(N)

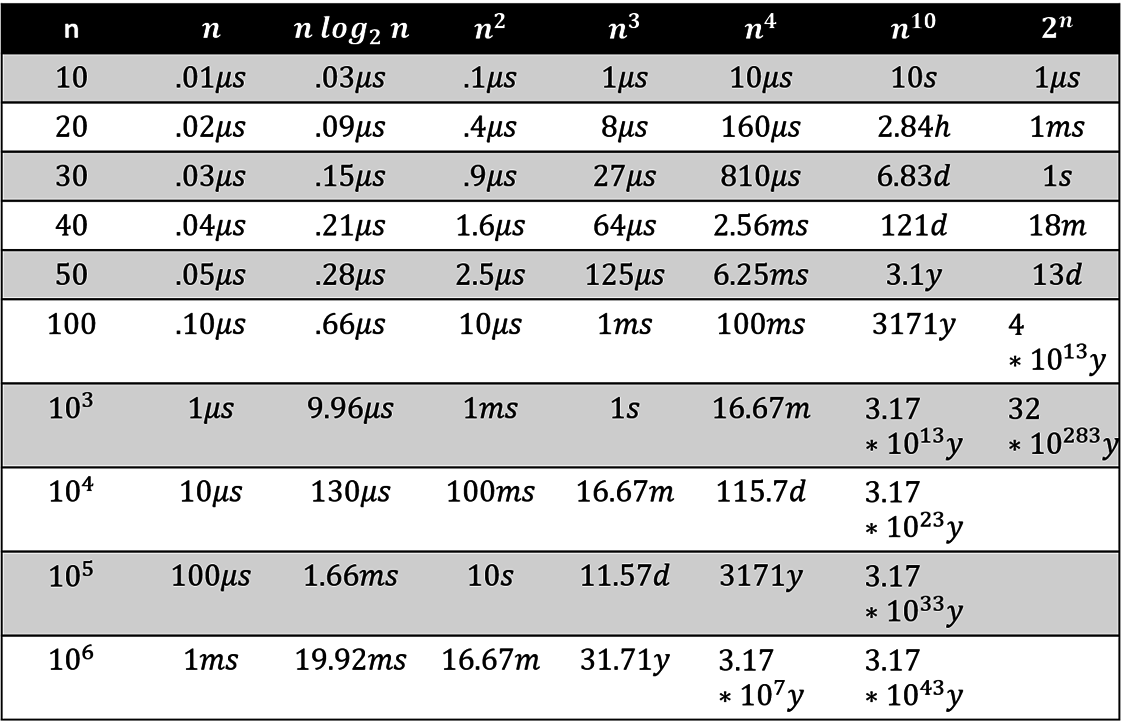
知道了複雜度

但它要跑多久?

假設我們的電腦每秒可以做10億次運算

time complexity

By allenwhale

Made with Slides.com

time complexity

  • 465

More from allenwhale