A Self Similar Model for Core Collapse Supernovae Shock Waves
Almog Yalinewich - Caltech Tea Talk 14.9.20
Plan of the Talk
- Introduction to core collapse supernovae
- Introduction to self similar solutions
- Self Similar Model for a core collapse supernova shock wave
- Implications for core collapse supernovae
Introduction to Core Collapse Supernovae
Why do we care?
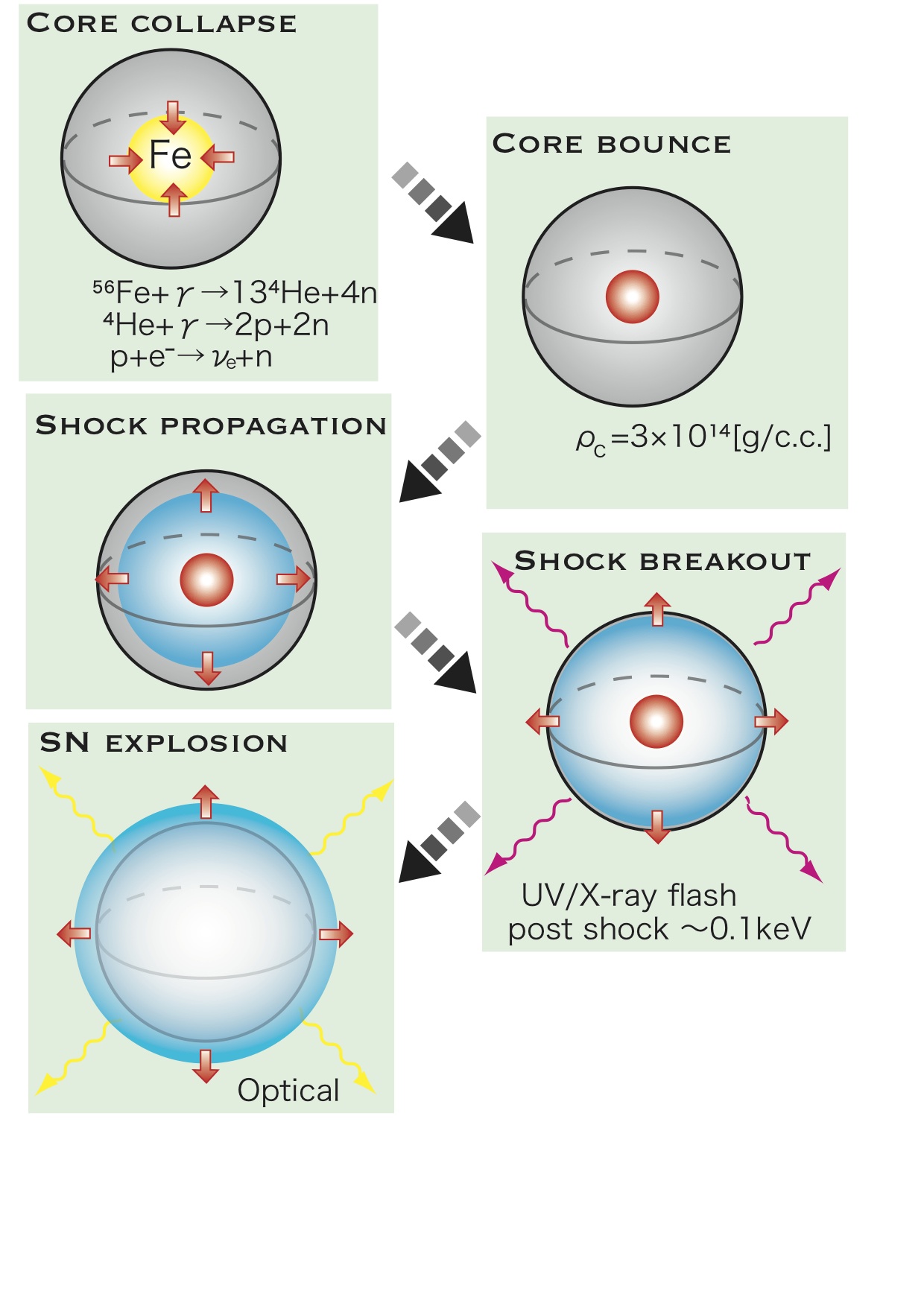
Stellar Evolution
Intro to the "Bee Movie" (2007)
physics
star
explode
The energy released is
star
explodes
stars
State of affairs in the previous millennium
1D sims bomb
2/3D sims explode
Couch 2017
Turbulence
Couch 2017
Turbulence doesn't add more energy to the system, so how does it help the star explode?
Borrielloa et al 2014
The problem with Simulations
Borrielloa et al 2014
- Expensive
- Volatile
- Not reproducible
Introduction to Self Similar Solutions
Origin Story
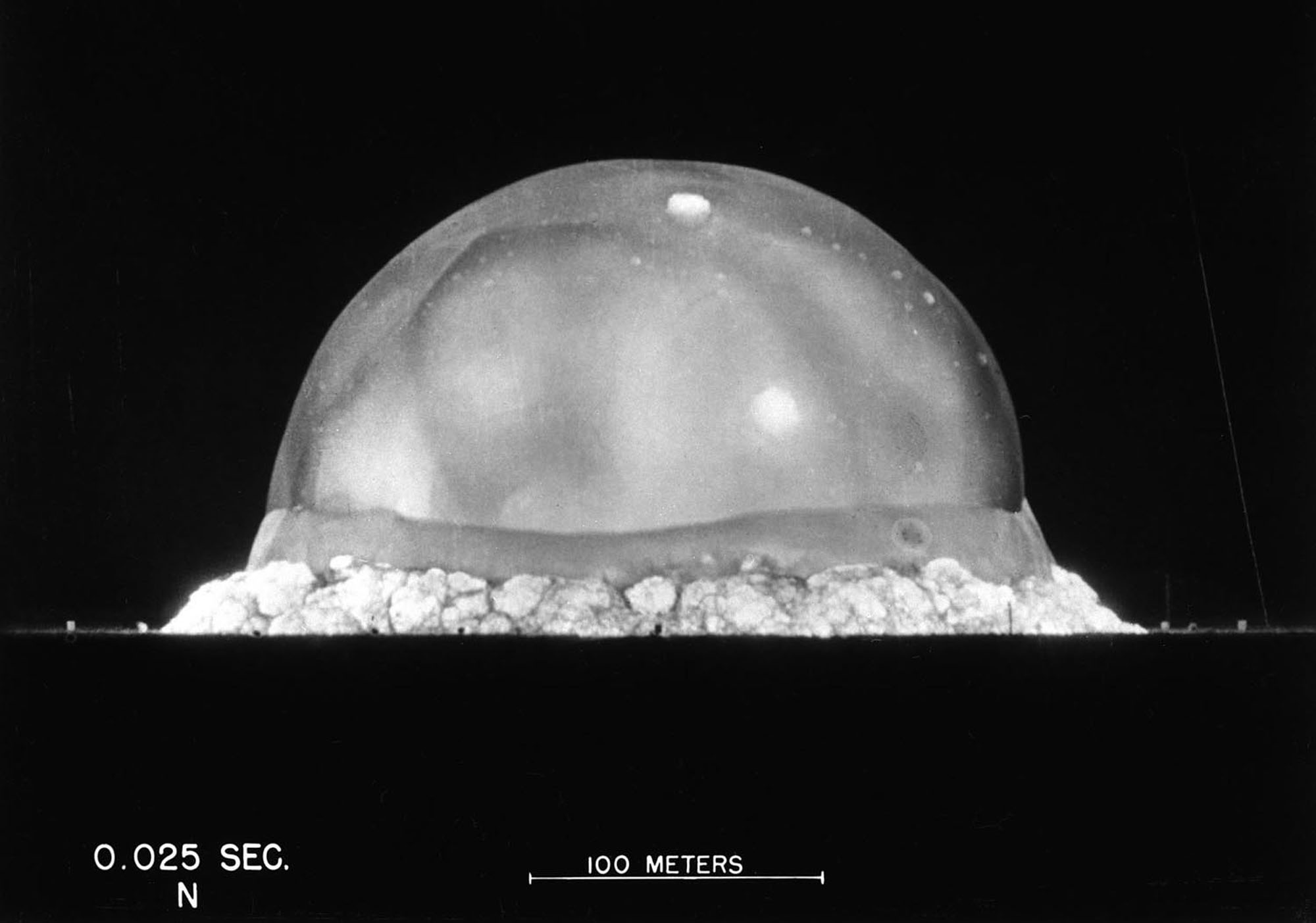
Scaling Relations
E \approx M V^2
E \approx \left(\rho_0 R^3\right) \left(R/t\right)^2
R \approx \left(\frac{E}{\rho_0} t^2\right)^{1/5}
Self Similarity
Suzuki & Shigeyama 2014
Hydrodynamic Equations
\frac{\partial \rho}{\partial t} + \frac{1}{r^2} \frac{\partial}{\partial r} \left(\rho v r^2\right) = 0
\frac{\partial v}{\partial t} + v \frac{\partial v}{\partial t} + \frac{1}{\rho} \frac{\partial p}{\partial r} = 0
\frac{\partial s}{\partial t} + v \frac{\partial s}{\partial r} = 0
s = \ln p - \gamma \ln \rho
c = \sqrt{\gamma p / \rho}
Reduction to ODES
\xi = \frac{r}{R}
\rho = \rho_0 G \left(\xi\right)
v = \dot{R} \xi V\left(\xi \right)
c = \dot{R} \xi C\left(\xi \right)
\xi G{\left(\xi \right)} \frac{d}{d \xi} V{\left(\xi \right)} + \xi V{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} - \xi \frac{d}{d \xi} G{\left(\xi \right)} + 3 G{\left(\xi \right)} V{\left(\xi \right)} = 0
\gamma \left(- 2 \xi \frac{d}{d \xi} V{\left(\xi \right)} + 2 \left(\xi \frac{d}{d \xi} V{\left(\xi \right)} + V{\left(\xi \right)}\right) V{\left(\xi \right)} - 5 V{\left(\xi \right)}\right) G{\left(\xi \right)} + 2 \left(\xi C{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} + 2 \xi G{\left(\xi \right)} \frac{d}{d \xi} C{\left(\xi \right)} + 2 C{\left(\xi \right)} G{\left(\xi \right)}\right) C{\left(\xi \right)} = 0
2 \gamma \left(- \gamma \xi C{\left(\xi \right)} V{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} + \gamma \xi C{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} + \xi C{\left(\xi \right)} V{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} - \xi C{\left(\xi \right)} \frac{d}{d \xi} G{\left(\xi \right)} + 2 \xi G{\left(\xi \right)} V{\left(\xi \right)} \frac{d}{d \xi} C{\left(\xi \right)} - 2 \xi G{\left(\xi \right)} \frac{d}{d \xi} C{\left(\xi \right)} + 2 C{\left(\xi \right)} G{\left(\xi \right)} V{\left(\xi \right)} - 5 C{\left(\xi \right)} G{\left(\xi \right)}\right) = 0
Boundary Conditions
G \left(1\right) = \frac{\gamma+1}{\gamma-1}
V \left(1\right) = \frac{2}{\gamma+1}
C \left(1\right) = \frac{\sqrt{2 \gamma \left(\gamma-1\right)}}{\gamma+1}
Rankine Hugoniot conditions for a strong shock
Hydrodynamic profiles
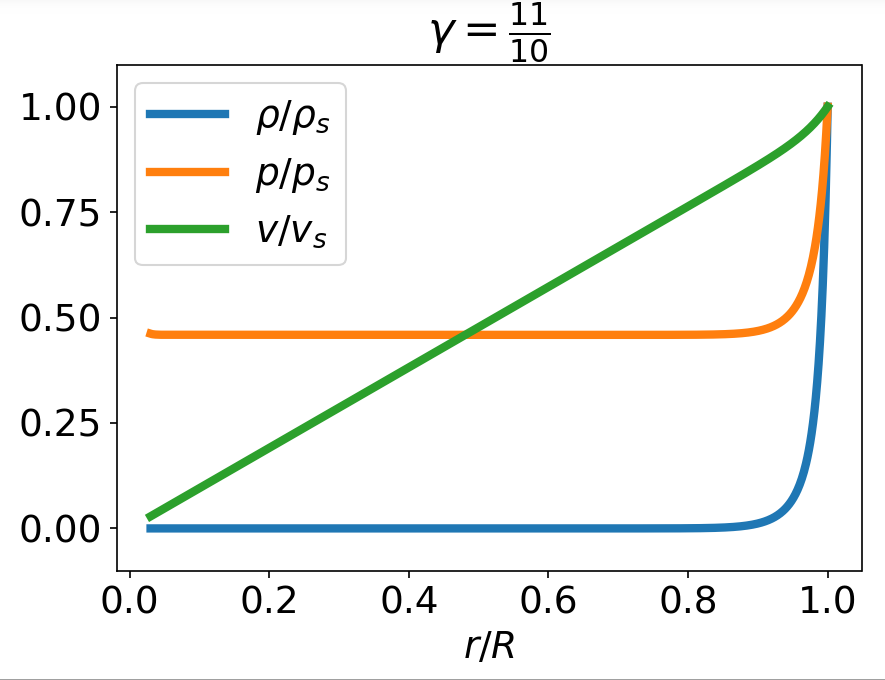
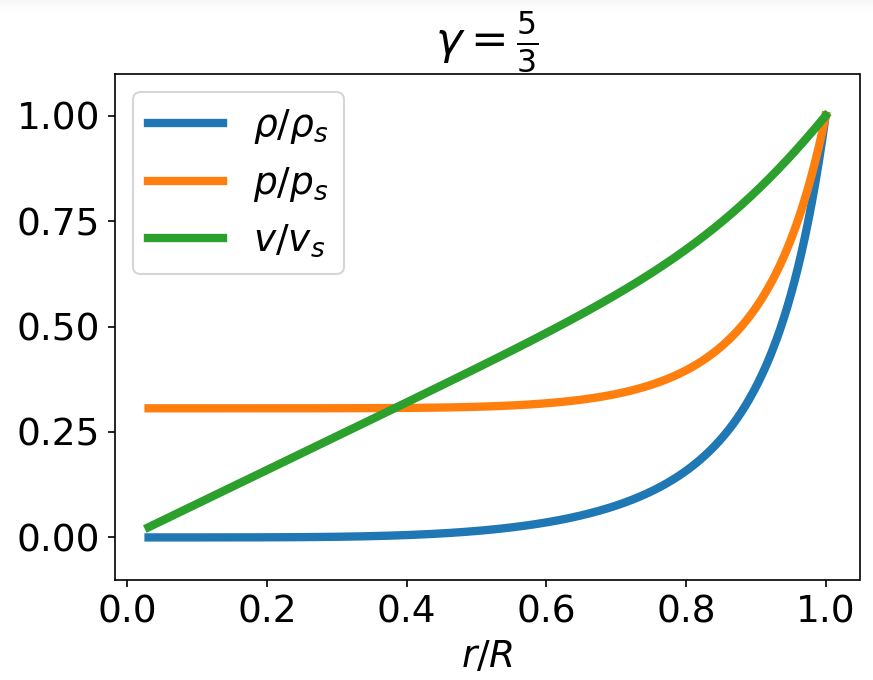
Energy Integral
\frac{E}{4 \pi \rho R^3 \dot{R}^2} = \int_0^{1} \xi^4 d \xi G \left(\frac{V^2}{2} + \frac{C^2}{\gamma-1}\right)
Thin shell approximation
E = \frac{4 \pi}{3} R^3 \frac{p}{\gamma-1}
M = \frac{4 \pi}{3} R^3 \rho_0
\frac{d}{d t} \left(M \dot{R} \right) = 4 \pi R^2 p
\dot{R} = \sqrt{\frac{3}{2 \pi} \left(\gamma-1\right) \frac{E}{\rho_0 R^3}} \Rightarrow R = \sqrt[5]{\frac{75}{8 \pi} \left(\gamma-1\right) \frac{E}{\rho_0} t^2}
Graded Density Profile
\rho_a = k r^{-\omega}
E \approx k R^{3-\omega} \left(R/t\right)^2
R \approx \left(E t^2/k\right)^{\frac{1}{5-\omega}}
Self Similar Model for a core collapse supernova shock wave
Scaling Relations
Explosion + point gravity
Breaks self similarity
Except for special set of parameters
r \approx \left(\mathcal{G} M t^2\right)^{1/3}
Free fall trajectory
Graded density trajectory
r \approx \left(E t^2/k\right)^{\frac{1}{5-\omega}}
\omega = 2
Virial parameter
\epsilon = \frac{E}{4 \pi \mathcal{G} M k}
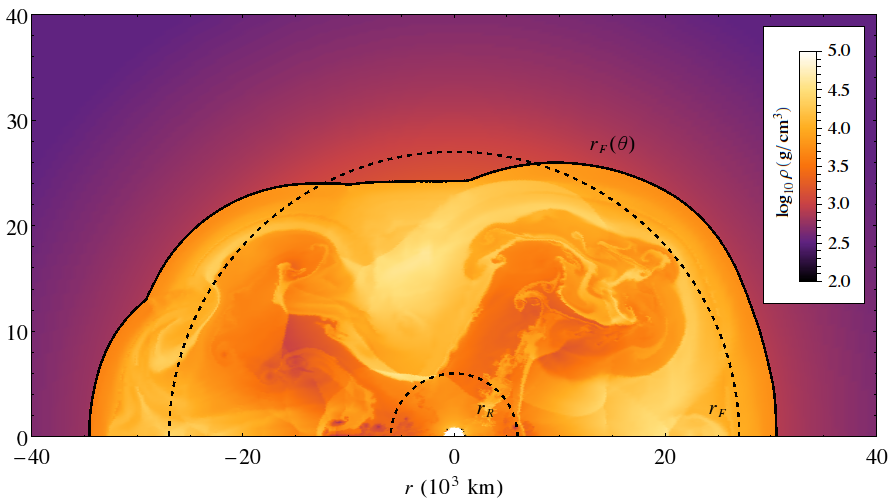
This is a realistic profile
Mezzacappa et al. 2001
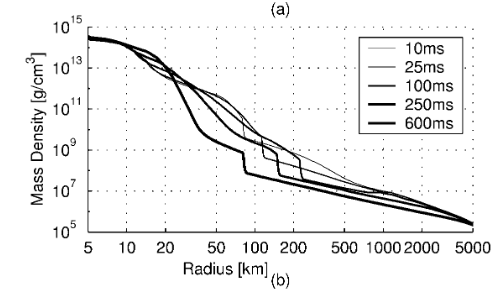
Pre - Explosion profile
Janka et al. 2012
Hydrodynamic Equations
\frac{\partial \rho}{\partial t} + \frac{1}{r^2} \frac{\partial}{\partial r} \left(\rho v r^2\right) = 0
\frac{\partial v}{\partial lt} + v \frac{\partial v}{\partial t} + \frac{1}{\rho} \frac{\partial p}{\partial r} = \color{cyan}-\frac{\mathcal{G} M}{r^2}
\frac{\partial s}{\partial t} + v \frac{\partial s}{\partial r} = 0
s = \ln p - \gamma \ln \rho
c = \sqrt{\gamma p / \rho}
Reduction to ODEs
R = \varpi \left(\mathcal{G} M t^2 \right)^{1/3}
\rho = k R^{-2} G \left(\xi\right), \, v = \dot{R} V \left(\xi\right), \, c = \dot{R} C \left(\xi\right)
\frac{G'\left(\xi\right)}{G\left(\xi\right)} = \frac{\left(8 \gamma \varpi^{3} \xi \left(\xi - V\right)^{3} + \gamma \left(\xi - V\right) \left(2 \varpi^{3} \xi^{2} V - 81\right) + \varpi^{3} \xi^{2} \left(12 - 8 \gamma\right) C^{2}\right)}{4 \varpi^{3} \xi^{2} \left(- \gamma \left(\xi - V\right)^{3} + \left(\xi - V\right) C^{2}{\left(\xi \right)} + \left(\gamma \xi - \gamma V - \xi + V\right) C^{2}\right)}
V'\left(\xi\right) = \frac{- 8 C^{2} V \gamma \varpi^{3} \xi + 12 C^{2} \varpi^{3} \xi^{2} - 2 V^{2} \gamma \varpi^{3} \xi^{2} + 2 V \gamma \varpi^{3} \xi^{3} + 81 V \gamma - 81 \gamma \xi}{4 \gamma \varpi^{3} \xi^{2} \left(C^{2} - V^{2} + 2 V \xi - \xi^{2}\right)}
C'\left(\xi\right) = \frac{C \left(8 \gamma \varpi^{3} \xi \left(V - \xi\right)^{2} \left(V \gamma - V - \gamma \xi + \xi\right) + \gamma \left(2 V \varpi^{3} \xi^{2} - 81\right) \left(V \gamma - V - \gamma \xi + \xi\right) - 4 \varpi^{3} \xi^{2} \left(C^{2} - \gamma \left(V - \xi\right)^{2}\right) \left(2 \gamma - 3\right)\right)}{8 \varpi^{3} \xi^{2} \left(C^{2} \left(V - \xi\right) + C^{2} \left(V \gamma - V - \gamma \xi + \xi\right) - \gamma \left(V - \xi\right)^{3}\right)}
\xi = r / R
Boundary Conditions
\frac{\rho_d}{\rho_u} = \frac{\gamma+1}{\gamma-1}
\frac{v_d}{v_u} = \frac{\gamma-1}{\gamma+1}
p_d = \rho_u v_u \left(v_u-v_d\right)
Rankine Hugoniot for a strong shock
But the upstream material is also affected by gravity
Free fall trajectory
\ddot{r} = - \frac{\mathcal{G} M}{r^2}
\sqrt{\frac{2 \mathcal{G} M}{r_0^3}} t = \sqrt{\frac{r}{r_0} \left(1-\frac{r}{r_0}\right)} + \cos^{-1} \left(\sqrt{\frac{r}{r_0}}\right)
x = r/r_0
Useful parameter: current to original radius ratio
\frac{\mathcal{G} M}{r} - \frac{\mathcal{G} M}{r_0} = \frac{1}{2} \dot{r}^2
\chi = R/r_0
Compression
\frac{\Delta r}{\Delta r_0} = \sigma \left(x\right) = \frac{3-x}{2} + \frac{3 \sqrt{1 - x} \cos^{-1}{\left(\sqrt{x} \right)}}{2 \sqrt{x}}
\rho = \rho_a \left(r_0\right) \frac{r_0^2 \Delta r_0}{r^2 \Delta r} = \frac{\rho_a \left(r/x\right)}{x^2 \sigma \left(x\right)}
\lim_{x \rightarrow 1} \sigma \left(x\right) = 1
\sigma \left(x\ll1\right) \approx \frac{3 \pi}{4 \sqrt{x}}
Shock Trajectory
R = \varpi \left(\chi \right) \left(\mathcal{G} M t^2\right)^{1/3}
\varpi \left(\chi\right) = \sqrt[3]{2} \chi \left(\sqrt{\chi} \sqrt{1 - \chi} + \cos^{-1} {\left(\sqrt{\chi} \right)}\right)^{-\frac{2}{3}}
\dot{R} = \frac{2}{3} \varpi^{3/2} \sqrt{\frac{\mathcal{G} M}{R}}
Self Similar Boundary Conditions
G\left(1\right) = \frac{\gamma+1}{\gamma-1} \frac{1}{\sigma}
C \left(1\right) = \frac{\sqrt{2 \gamma \left(\gamma-1\right)}}{\gamma+1} \left(1+\frac{3 \sqrt{2}}{\varpi^{3/2}} \sqrt{\frac{1}{\chi} - 1}\right)
V \left(1\right) = \frac{2}{\gamma+1} - \frac{\gamma-1}{\gamma+1} \frac{3 \sqrt{2}}{\varpi^{3/2}} \sqrt{\frac{1}{\chi}-1}
Hydrodynamic Profiles
\chi = 0.1
\gamma = 1.01
\chi = 0.1
\gamma = 4/3
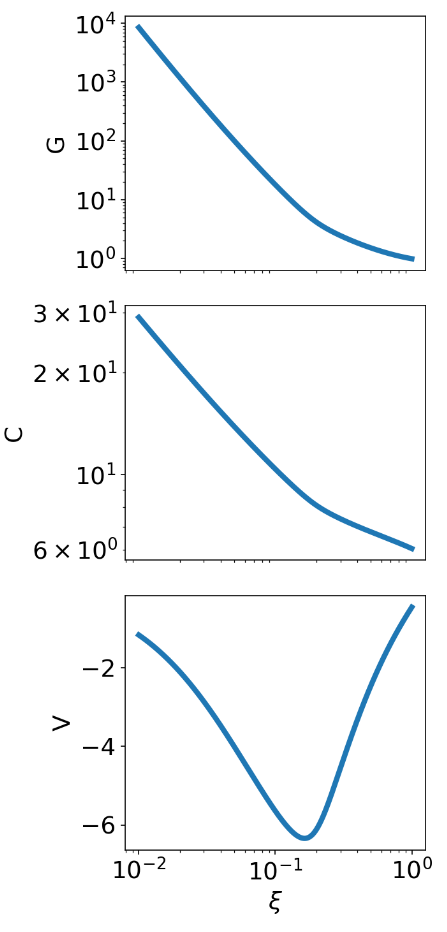
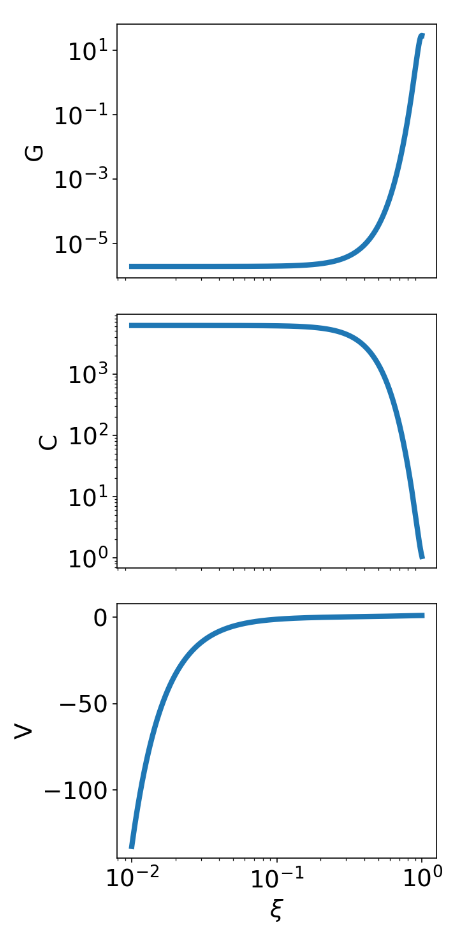
Energy Integral
E = \int_0^{R} 4 \pi r^2 dr \rho \left(\frac{1}{2} v^2 + \frac{c^2}{\gamma \left(\gamma-1\right)} - {\color{cyan}\frac{\mathcal{G} M}{r}}\right) =
= \frac{16 \pi}{9} k \mathcal{G} M \varpi^3 \int_0^1 \xi^2 d \xi G \left(\frac{V^2}{2} + \frac{C^2}{\gamma\left(\gamma-1\right)} - {\color{cyan}\frac{9}{4 \varpi^3 \xi}}\right)
Energy Curve
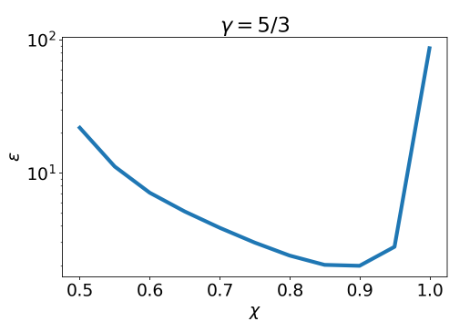
Phase Diagramme
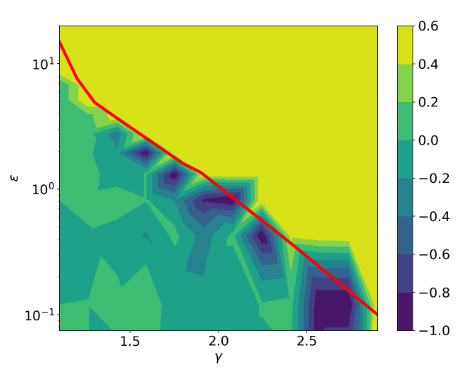
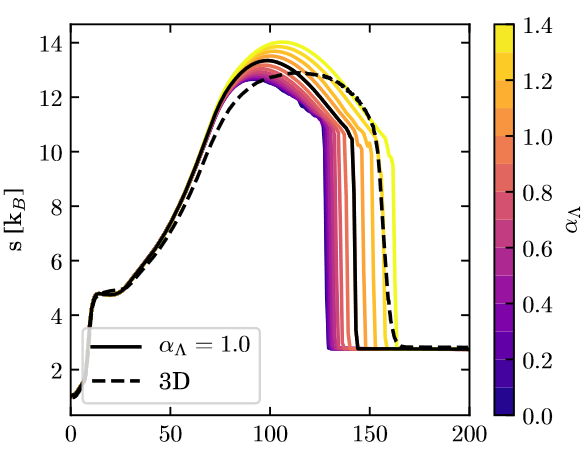
The Role of Turbulence
More diffusion is like higher gamma
Couch et al 2020
Implications for Core Collapse Supernovae
Neglected Effects
- Neutrino heating
- turbulence
- radiation transfer
- nuclear reactions
- semi degenerate
equation of state - Acoustic waves in the shocked region
(Gossan, Fuller & Roberts 2019)
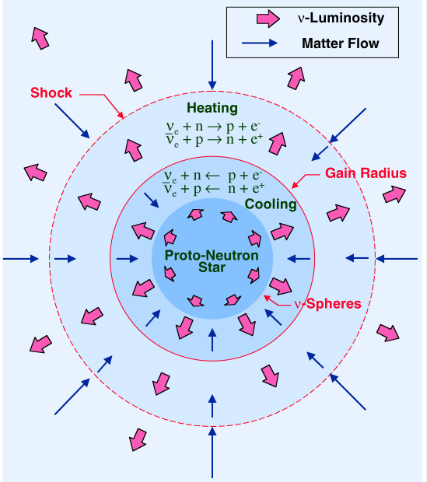
Heating
E \approx Q t^q \approx k R^{3-\omega} \dot{R}^2
R \propto t^{\frac{2+q}{5-\omega}}
q=1 \Rightarrow \omega = \frac{1}{2}
Turbulent Diffusion
\nu \propto R \dot{R}
Model like the Shakura Sunyaev alpha model
Classical diffusion breaks self similarity
workaround:
Higher order effect
Optical depth
>
Ideal shock
\tau \propto \int \rho \, dr
Turbulent shock
Conclusion
An analytic self similar model for a core collapse supernovae
Critical energy, depending on shock structure
Turbulent shock more resilient against gravity
Model can be improved within self similar framework
Questions?
A self Similar...
By almog yalinewich
