Binary Classification Two-Sample Test (C2STs) with Logistic Regression
CPSC 532S - Danica Sutherland
James, Amin, James
James
- Riddell1
Finding bounds for p-value
- Imagine we have trained a classifier on our data.
- We then compute the (pseudo) t-statistic using a test set .
- Then we calculate the p-value using the following function:
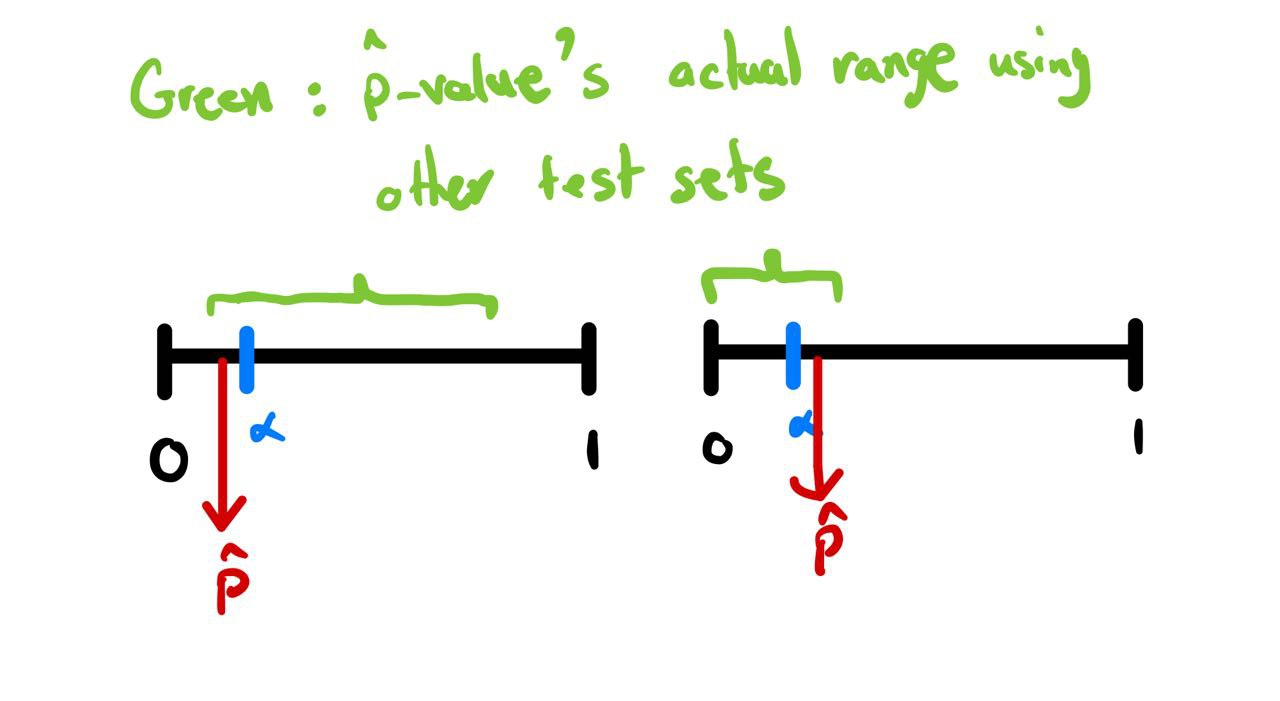
- But, how confident are we that our p-value will be almost the same, if we change the test set?
- Possible scenarios:
D_{te}
\Gamma(t) = Pr(T \ge t | H_0)
Finding bounds for p-value
Finding Bounds: Linear Classifiers
- Let's start with a simple case:
- Take the space of linear classifiers:
- Use 0-1 loss:
- Let's derive the (pseudo) t-statistic of this classifier:
- Note that:
- Idea: if we find some bounds for , we can use them to find bounds for our reported p-value.
\mathcal{H} = \{\langle w, x \rangle\}
l(h, (x, y)) = \mathbb{I}(sign(h(x)) = y)
\hat{t} = \frac{1}{n_{te}}\sum_{(x, y) \sim D_{te}}\mathbb{I}(sign(h(x)) \ne y)
L^{0-1}_{D_{te}}(h) = 1 - \hat{t}
L^{0-1}_{D_{te}}(h)
Finding Bounds for Linear Classifiers: Test Loss
- Let's start with the Uniform Convergence of Linear Classifiers trained with 0-1 loss:
-
We have the assumptions that:
-
We know that
-
Thus: [https://cse.buffalo.edu/~hungngo/classes/2011/Fall-694/lectures/rademacher.pdf]
-
Using this, we can derive the uniform convergence bounds:
\mathcal{H} = \{\langle w, x \rangle\} \qquad \mathcal{G} = {\ell^{0-1} \circ \mathcal{H}}
VCdim(\mathcal{H}) = d \Longrightarrow \mathcal{R}_n(\mathcal{H}) \le \sqrt{\frac{2\, d \, log(n)}{n}}
\mathcal{R}_n(\mathcal{G}) \le \frac{1}{2} \sqrt{\frac{2\, d \, log(n)}{n}} + \frac{1}{2\sqrt{n}}
\Longrightarrow \sup_{h\in\mathcal{H}} | L^{0-1}_S(g)) - L^{0-1}_D(g))| \le \sqrt{\frac{2\, d \, log(n)}{n}} + \frac{1}{\sqrt{n}} + \sqrt{\frac{1}{2n} \log\frac{1}{\delta}} \text{ w.p. } 1-\delta
Finding Bounds for Linear Classifiers: Test Loss
- But, how do we derive bounds for test loss?
-
Remember that:
-
Combining this with the uniform convergence property, we get:
- Remember that
- We get:
- Note that is a monotonically decreasing function, Thus:
L^{0-1}_S(g) - \varepsilon_1(n, \delta_1) - \varepsilon_2(n_{te}, \delta_2) \le L^{0-1}_{D^{te}}(g) \le L^{0-1}_S(g) + \varepsilon_1(n, \delta_1) + \varepsilon_2(n_{te}, \delta_2)
|L_{V}(h) - L_{D}(h)| \le \sqrt{\frac{1}{2|V|}\log\frac{2}{\delta}} \text{ w.p. } 1-\delta
L^{0-1}_{D_{te}}(g) = 1-\hat{t}
t_{tr} - \varepsilon_1(n, \delta_1) - \varepsilon_2(n_{te}, \delta_2) \le \hat{t} \le t_{tr} + \varepsilon_1(n, \delta_1) + \varepsilon_2(n_{te}, \delta_2)
\Gamma(t) = 1 - CDF_{N(0, 1)}(t)
\Gamma(t_{tr} + \varepsilon(n^*, \delta^*)) \le \hat{p} \le \Gamma(t_{tr} - \varepsilon(n^*, \delta^*)) \text{ w.p. } 1 - \delta^*
Finding Bounds for Logistic Regression
- But, we can't really train classifiers on 0-1 loss.
- How about logistic loss? (Logistic Regression)
- Well, the (pseudo) t-statistic and the p-value computations are based on 0-1 loss...
- We would have to design a new test for other (pseudo) t-statistics.
- Idea: Use logistic loss as a surrogate loss for 0-1 Loss.
- The good: bounds for logistic regression!!!
- The ugly: One-sided bounds for logistic regression :(
- Because the surrogate loss bounds 0-1 loss only on one side
Finding Bounds for Logistic Regression
-
We showed that:
- Note that:
- Thus:
L^{0-1}_s(g) \le L_S^{log}(g) \Longrightarrow 1- L^{0-1}_s(g) \ge 1-L_S^{log}(g) \Longrightarrow t_{tr} \ge t_{tr}^{log}
t_{tr} - \varepsilon_1(n, \delta_1) - \varepsilon_2(n_{te}, \delta_2) \le \hat{t} \le t_{tr} + \varepsilon_1(n, \delta_1) + \varepsilon_2(n_{te}, \delta_2)
Binary Classification Two-Sample Test (C2STs) with Logistic RegressionCPSC 532S - Danica Sutherland
By Amin Mohamadi
