Variance Reduction and Convergence Analysis of BBVI
UBC CPSC 532F - Apri 2021
Mohamad Amin Mohamadi
Variational Inference
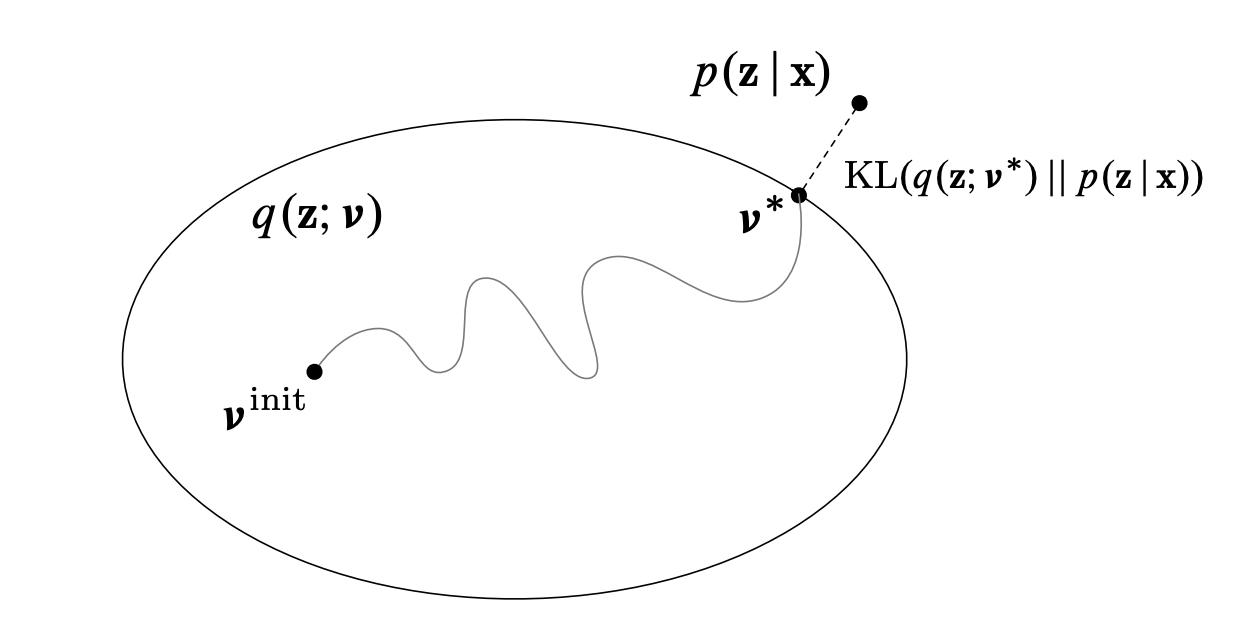
Blackbox Variational Inference
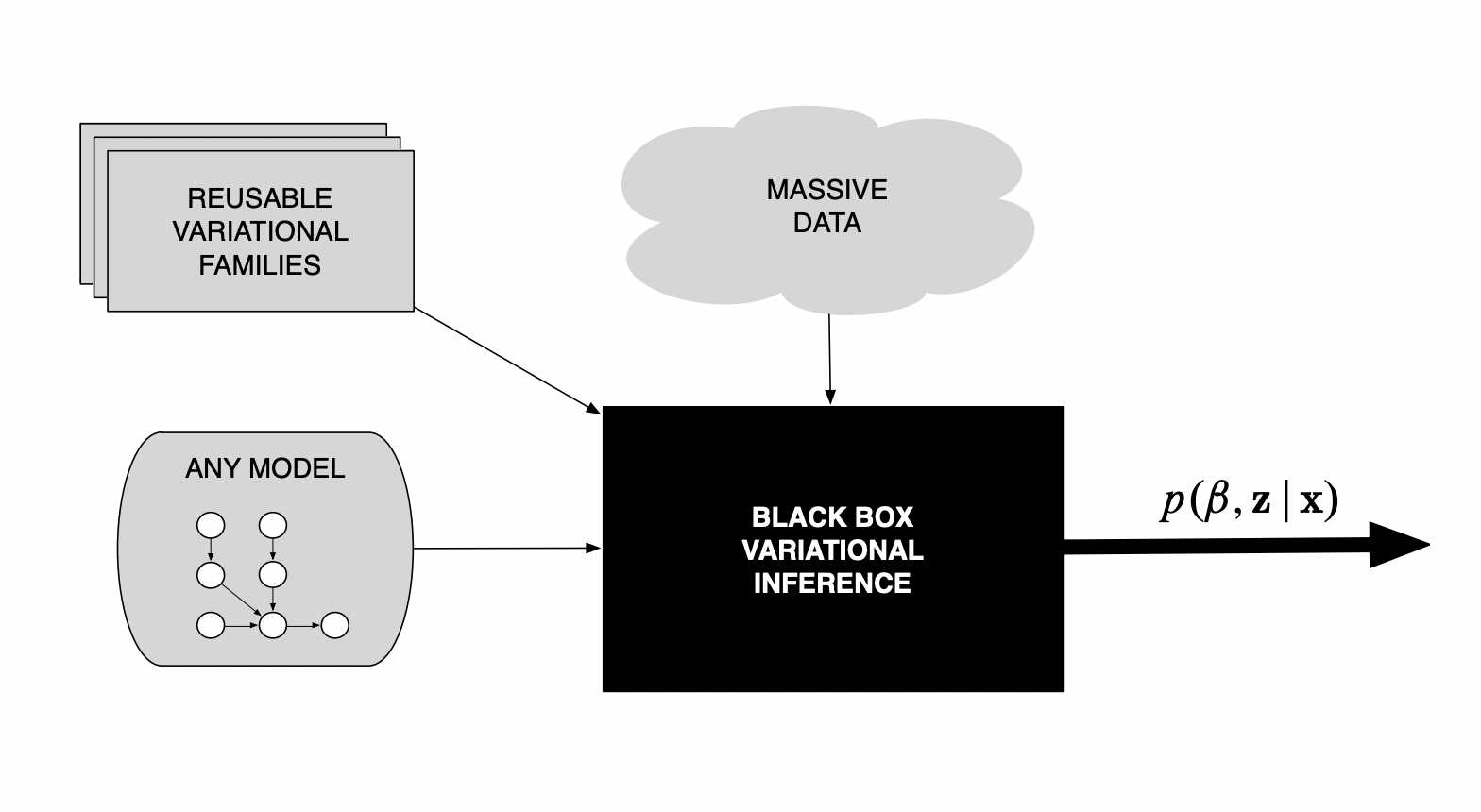
Blackbox Variational Inference
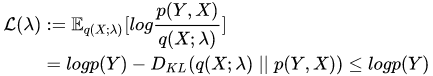
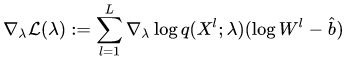
Implementation
- Using PyTorch's AutoGrad to calculate gradient of the ELBO
- Using PyTorch's Adam Optimizer to optimize the latent variables of the proposals
- Using PyTorch's distributions as proposals for posterior distribution
Variance Reduction Hypothesis
- Does the control variate actually help reducing the variance of the gradient?
- Is there any significant difference in terms of convergence between the variance reduced method and the normal method?
Convergence Analysis Hypothesis
- Does the Blackbox Variational Inference algorithm actually converge?
- How is the convergence rate comparable to the good old MCMC sampling methods?
Test 1: Simple Gaussian
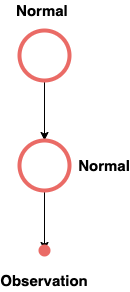
Gaussian(1, sqrt(5))
Gaussian( x , sqrt(2))
7, 8
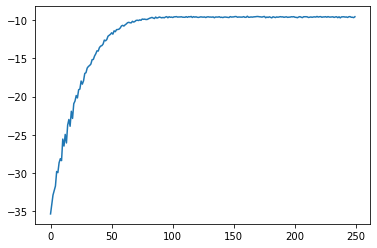
Model Negative Joint Log Likelihood Score Variance Reduced
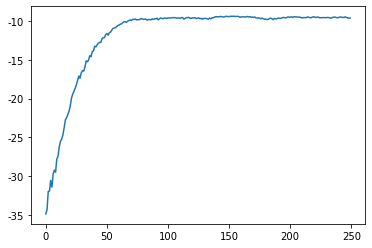
Model Negative Joint Log Likelihood Score Normal
Posterior Samples
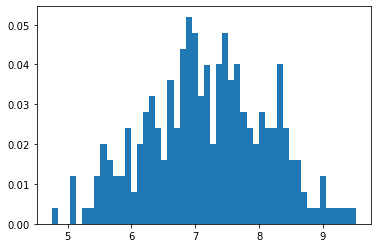
True Posterior Comparison
| True Values | Estimated | |
|---|---|---|
| Mean | 7.25 | 7.19 |
| STD | 0.91 | 0.88 |
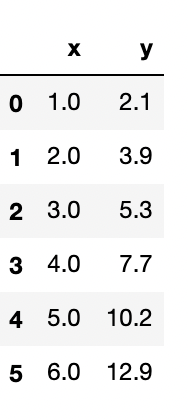
Test 2: Simple Bayesian Linear Regression
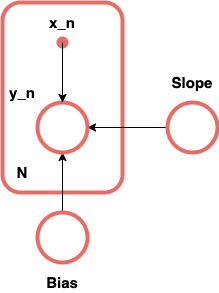
Gaussian(0, 10)
Gaussian(0, 10)

Model Negative Joint Log Likelihood Score Variance Reduced
Model Negative Joint Log Likelihood Score Normal

Posterior samples
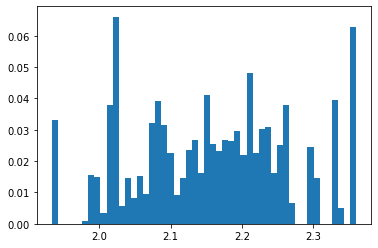
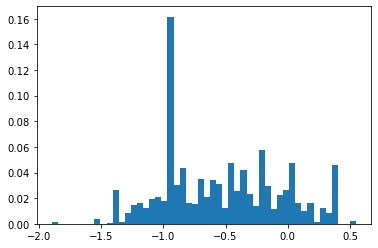
Slope
Bias
Test 3: Simple HMM
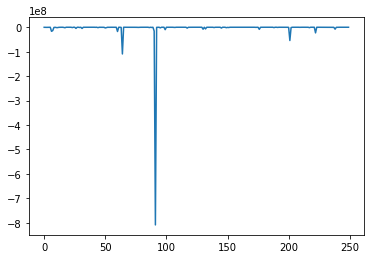
Model Negative Joint Log Likelihood Score Variance Reduced
Does not converge!
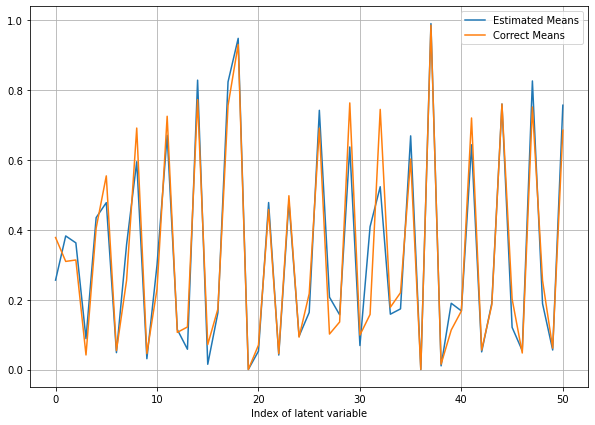
Importance Sampling Results
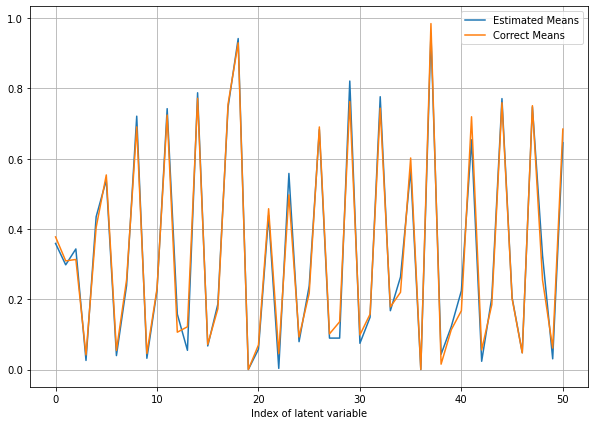
Metropolis Hastings Result
Conclusion
- As mentioned, the control variates are a promising way to reduce the variance of the score function, but in large models, like the HMM test case, it can not help save the model from extremely small likelihoods.
- Although the BBVI technique outperforms the classic sampling methods in small-moderate models and thanks to AutoGrad, it's automatic, it fails to converge to the posterior whereas classic methods still work.
Thank you!
deck
By Amin Mohamadi
deck
- 313



