A Fast, Well-Founded Approximation to the Empirical Neural Tangent Kernel
Amin - July 13
The Neural Tangent Kernel
- An important object in characterizing the training of suitably-initialized infinitely wide neural networks (NN)
- Describes the exact training dynamics of first-order Taylor expansion of any finite neural network:
- Is defined as
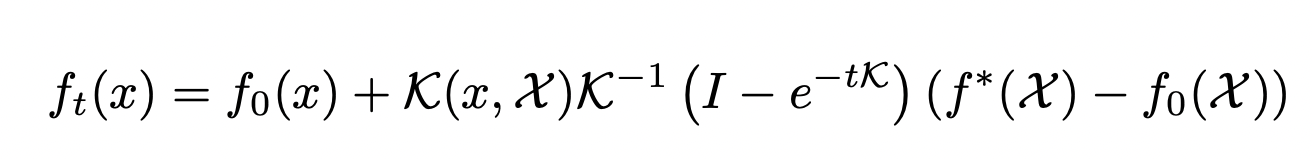
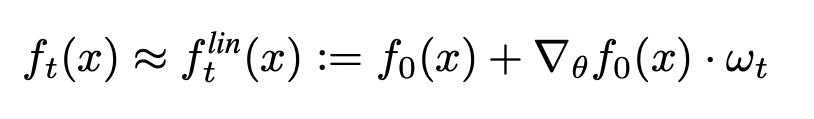
\Theta_f(x_1, x_2) = J_\theta f(x_1) {J_\theta f(x_2)}^\top
The Neural Tangent Kernel
-
Has enabled lots of theoretical insights into deep NNs:
- Studying the geometry of the loss landscape of NNs (Fort et al. 2020)
- Prediction and analyses of the uncertainty of a NN’s predictions (He et al. 2020, Adlam et al. 2020)
-
Has been impactful in diverse practical settings:
- Predicting the trainability and generalization capabilities of a NN (Xiao et al. 2018 and 2020)
- Neural Architecture Search (Park et a. 2020, Chen et al. 2021)
- *Your work here* :D
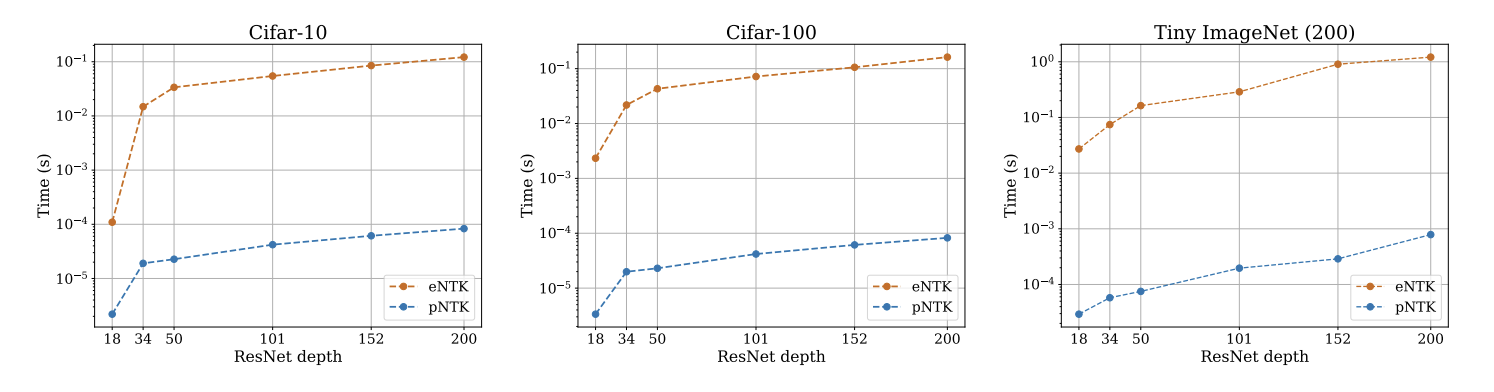
eNTK: Computational Cost
-
Is, however, notoriously expensive to compute :(
- Both in terms of computational complexity, and memory complexity!
- Computing the Full empirical NTK of ResNet18 on Cifar-10 requires over 1.8 terabytes of RAM !
-
This work:
- An approximation to the ENTK, dropping the O term from the above equations!
\underbrace{\Theta_f(X_1, X_2)}_{N_1 O \times N_2 O} = \underbrace{J_\theta f(X_1)}_{N_1 \times O \times P} \otimes \underbrace{{J_\theta f(X_2)}^\top}_{P \times O \times N_2}
pNTK: An Approximation to the eNTK
- For each NN, we define pNTK as follows:
(We are basically adding a fixed untrainable dense layer at the end of the neural network!)
- Computing this approximation requires O(O^2) less time and memory complexity in comparison to the eNTK. (Yay!)
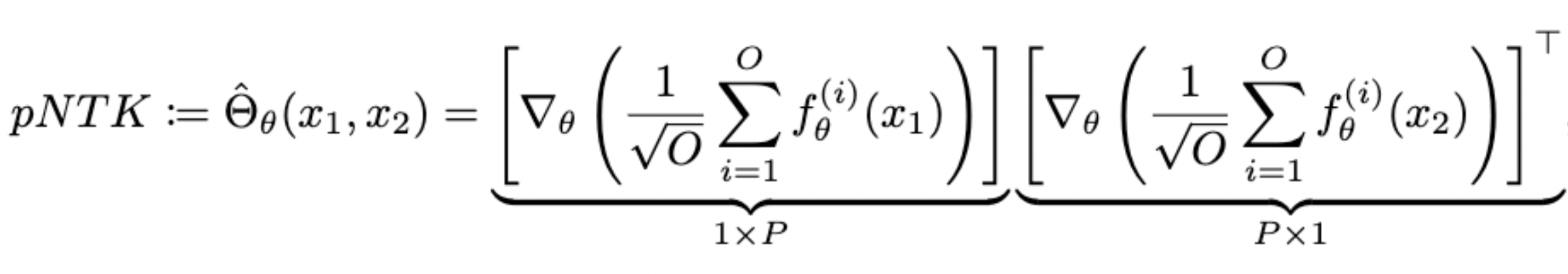
Computational Complexity: pNTK vs eNTK
pNTK: An Approximation to the eNTK
- Previous work already implies that for infinitely wide NNs at initialization, pNTK converges to the eNTK. In the infinitely wide regime, the eNTK of two datapoints is a diagonal matrix.
- Lots of recent papers have used the same property, but with little to no justification!
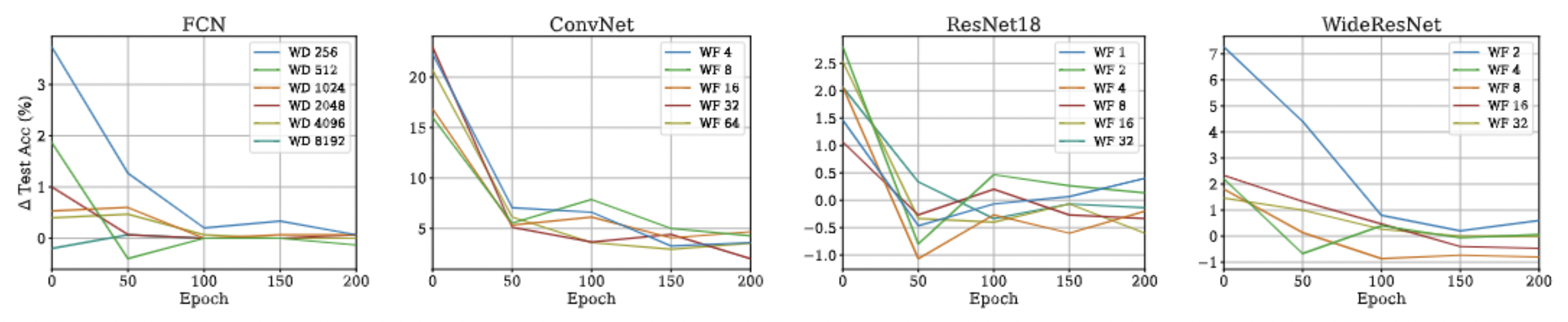
- We show that although this property is not valid in the finite width regime, it converges to the eNTK as width grows.
Approximation Quality: Frobenius Norm
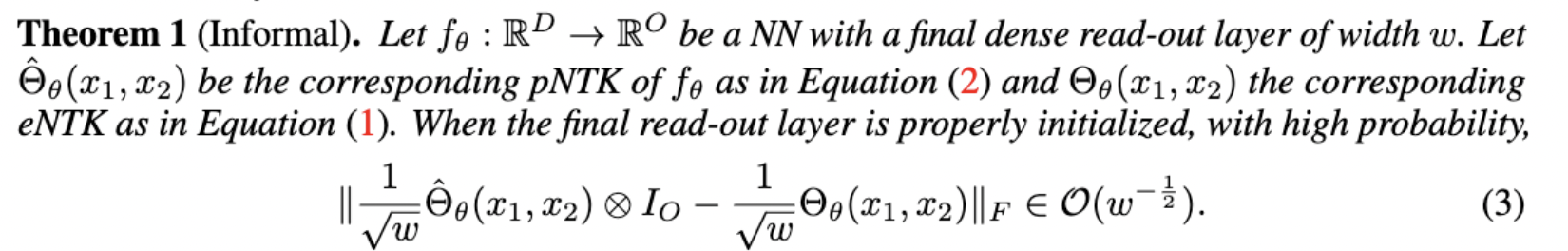
- Why?
- The diagonal elements of the difference matrix grow linearly with width
- The non-diagonal elements are constant with high probability
- Frobenius Norm of the difference matrix relatively converges to zero
Approximation Quality: Frobenius Norm
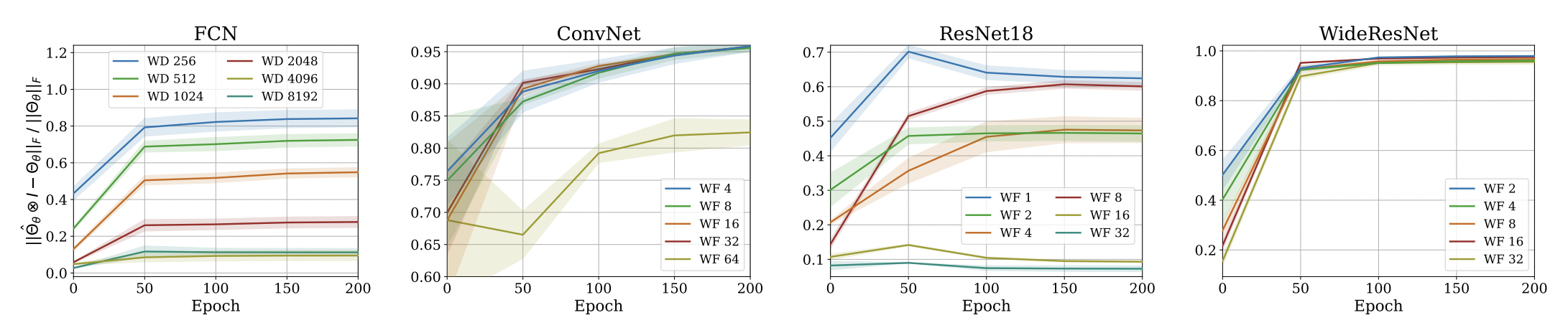
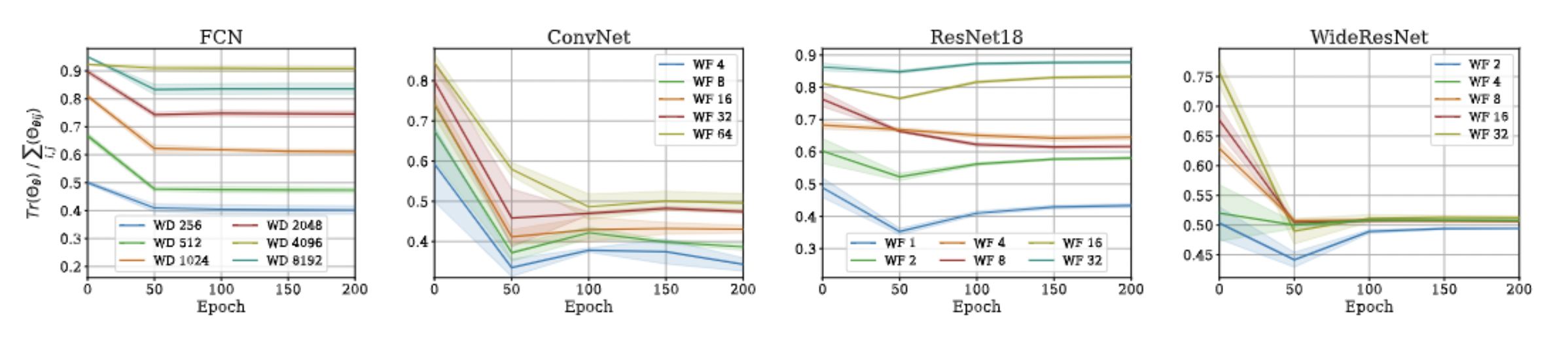
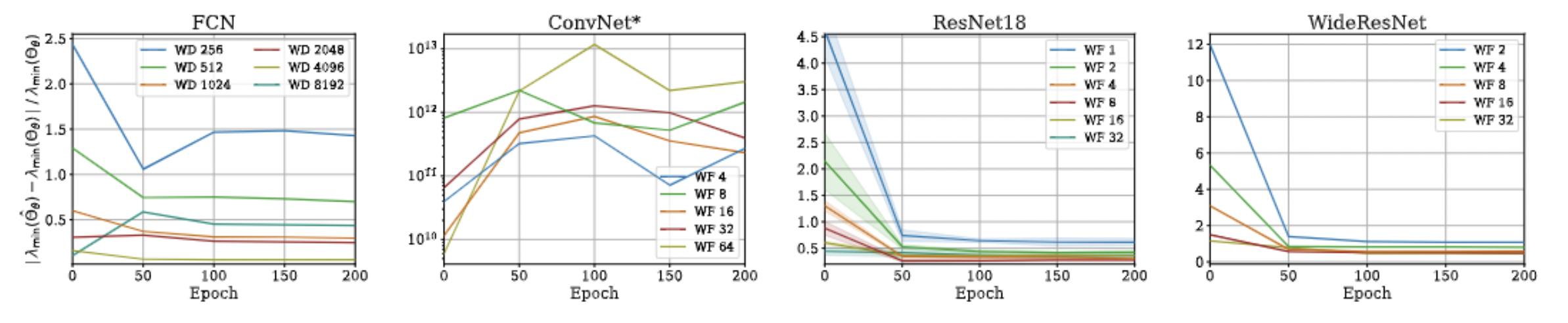
Approximation Quality: Eigen Spectrum

- Proof is very simple!
- Just a triangle inequality based on the previous result!
- Unfortunately, we could not come up with a similar bound for min eigenvalue and correspondingly the condition number, but empirical evaluations suggest that such a bound exists!
Approximation Quality: Eigen Spectrum
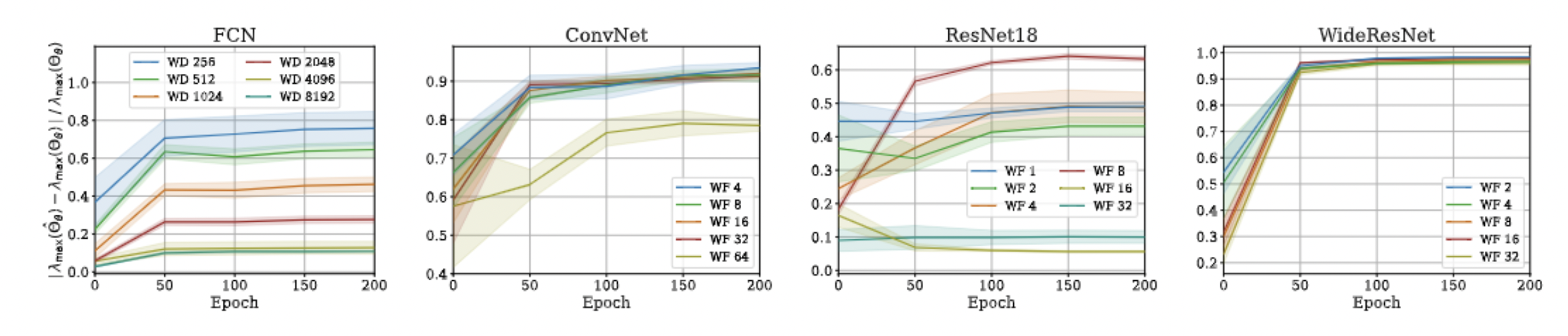
Approximation Quality: Kernel Regression
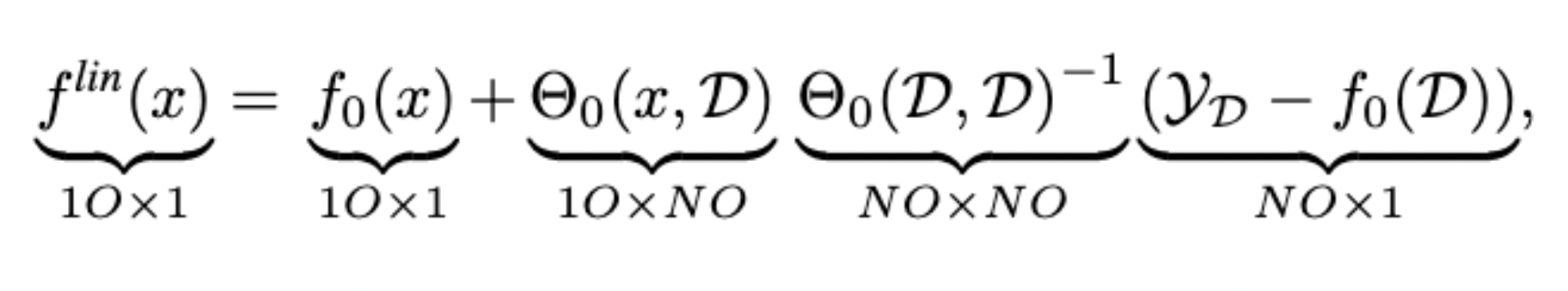
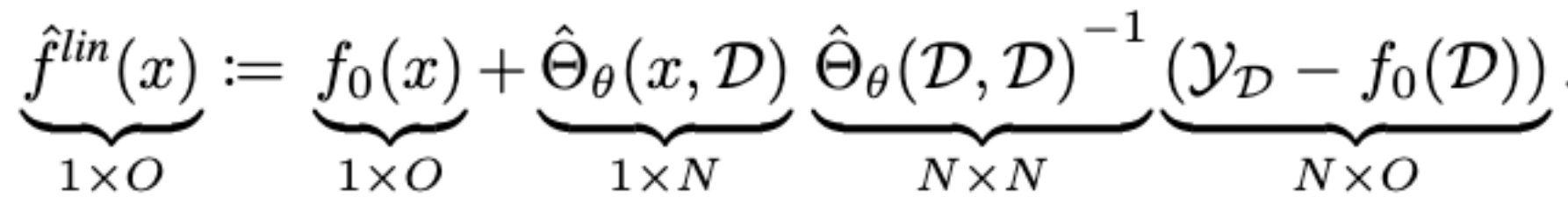
- Note that pNTK is a scalar-valued kernel, but the eNTK is a matrix-valued kernel!
- Intuitively, one might expect that they can not be used in the same context for kernel regression.
- But, there's a work-around, as this is a well known problem:
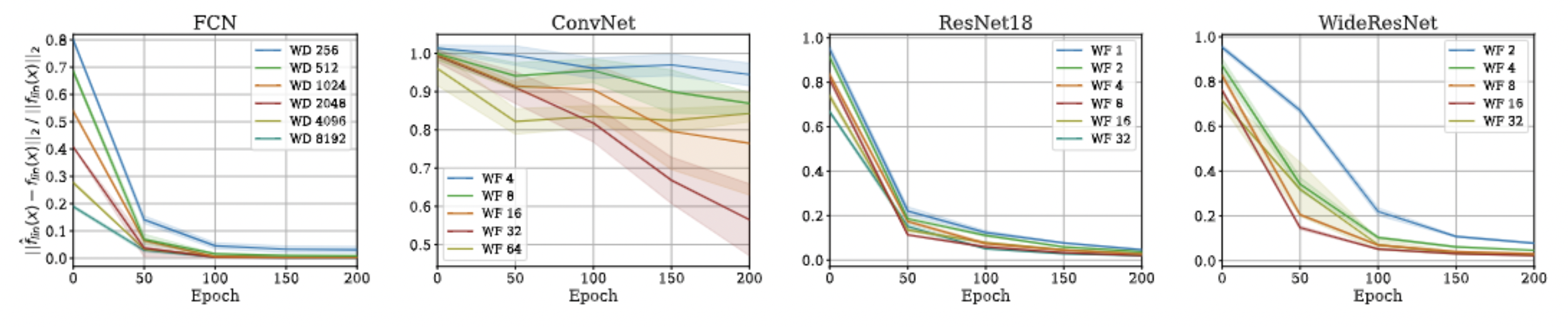
Approximation Quality: Kernel Regression

- Note: This approximation will not hold if there is any regularization (ridge) in the kernel regression! :(
- Note that we are not scaling the function values anymore!
Approximation Quality: Kernel Regression
Thank You! Questions?
Making
By Amin Mohamadi
Making
- 354



