Impact of weak lensing mass-mapping and baryonic effects on cosmology inference
Andreas Tersenov
WLSWG/SHE Joint Meeting, Marseille, 2 October 2025
Part 1
Impact of weak-lensing mass-mapping algorithms on cosmology inference
arXiv:2501.06961
with Lucie Baumont, Jean-Luc Starck & Martin Kilbinger
Weak Lensing Mass Mapping
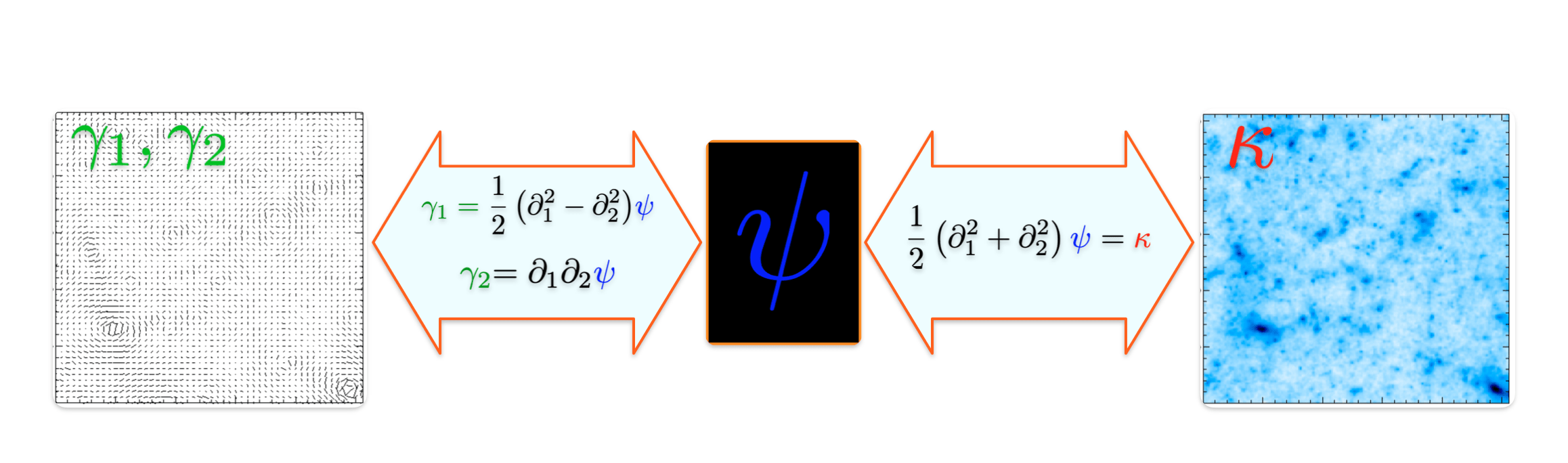
- From convergence to shear:
- From shear to convergence:
\gamma_i = \hat{P}_i \kappa
\kappa = \hat{P}_1 \gamma_1 + \hat{P}_2 \gamma_2
\hat{P}_1(k)=\dfrac{k_1^2 - k_2^2}{k^2}, \,\,
\hat{P}_2(k)=\dfrac{2k_1k_2}{k^2}
The mass-mapping problem
- Shear measurements are discrete, noisy, and irregularly sampled
- We actually measure the reduced shear
- Masks and integration over a subset of ℝ2 lead to border errors
- Convergence is recoverable up to a constant ⇒ mass-sheet degeneracy problem
Mass mapping is an ill-posed inverse problem
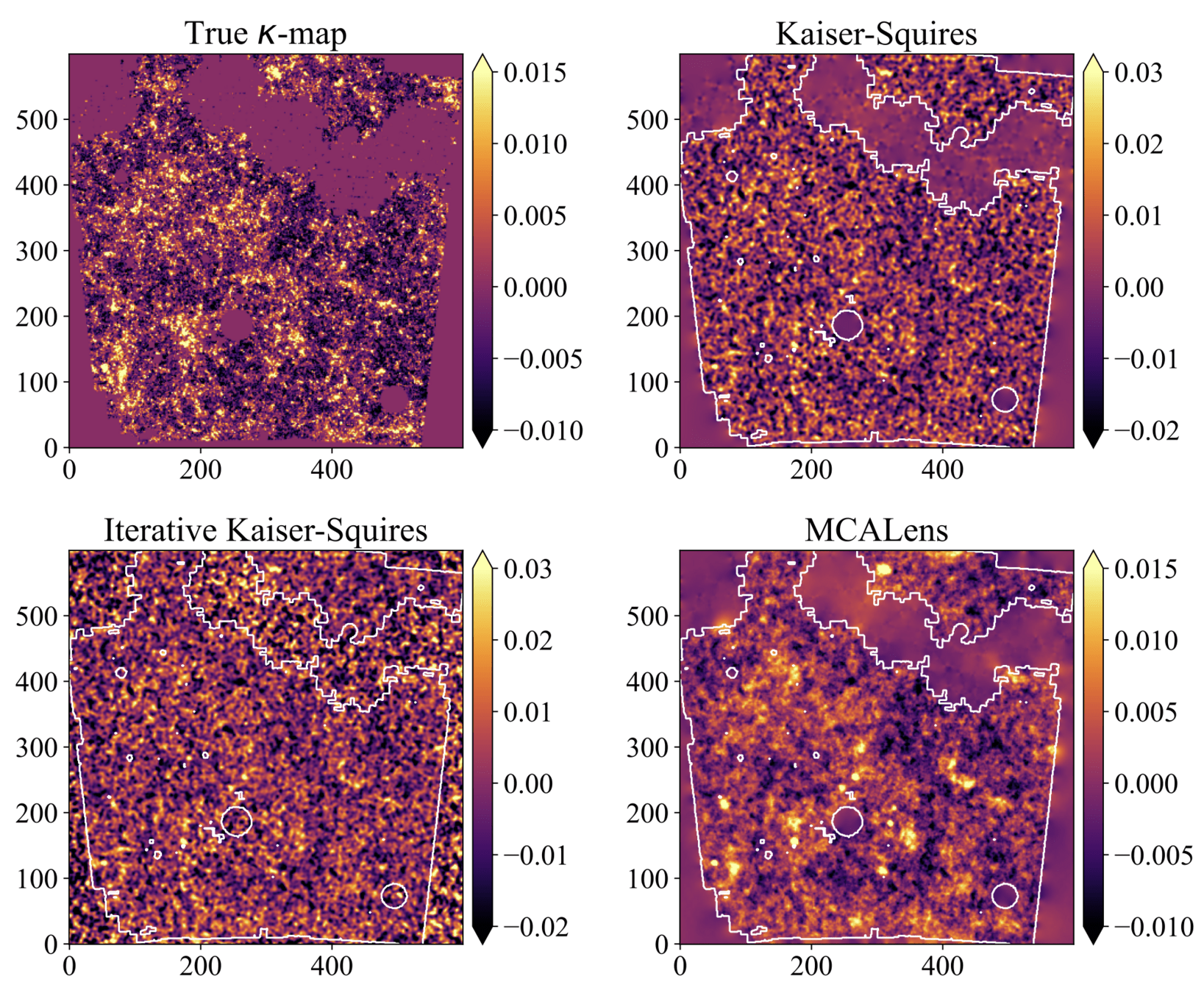
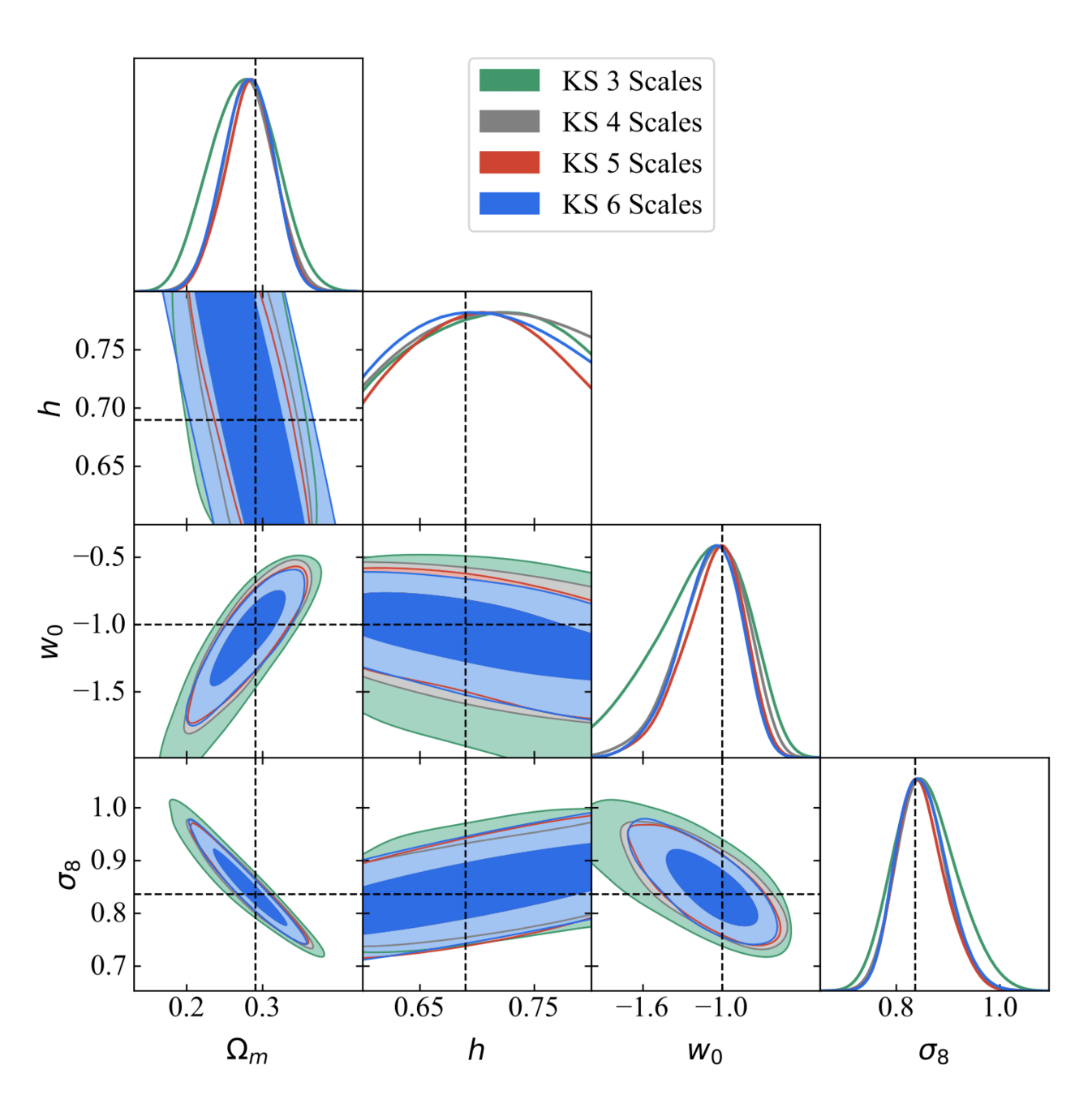
Different algorithms have been introduced, with different reconstruction fidelities, in terms of RMSE
Motivating this project:
- The various algorithms have different RMSE performance
- In cosmology we don't care about RMSE of mass maps, but only about the resulting cosmological parameters
⇒ This should be our final benchmark!
So... does the choice of the mass-mapping algorithm have an impact on the final inferred cosmological parameters?
Or as long as you apply the same method to both observations and simulations it won't matter?
cosmoSLICS pipeline
\begin{array}{ll}
\hline \hline
\text{Method} & \text{RMSE} \downarrow \\
\hline
\text{KS } & 1.1 \times 10^{-2} \\
\text{iKS } & 1.1 \times 10^{-2} \\
\text{MCALens} & 9.8 \times 10^{-3} \\
\hline
\end{array}
- Add realistic masks & Euclid-like noise to shear maps
- Use different algorithms for the mass mapping
- Compression with higher-order statistics (peaks)
- Gaussian Likelihood + MCMC
For which we have/assume an analytical likelihood function
x
t = f(x)
How to constrain cosmological parameters?
Likelihood → connects our compressed observations to the cosmological parameters
\underbrace{p\left(\theta \mid t=t_0\right)}_{\text {posterior }} \propto \underbrace{p\left(t=t_0 \mid \theta\right)}_{\text {likelihood }} \underbrace{p(\theta)}_{\text {prior }}
p\left(t=t_0 \mid \theta\right)
Credit: Justine Zeghal
2pt vs higher-order statistics
The traditional way of constraining cosmological parameters misses the non-Gaussian information in the field.
x
t = f(x)
DES Y3 Results
Credit: Justine Zeghal
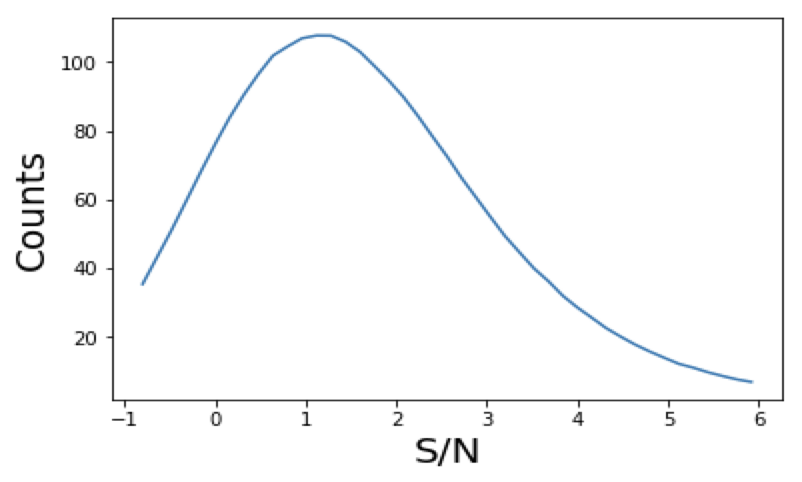
Higher Order Statistics: Peak Counts
=
+
+
+
+
- Peaks: local maxima of the SNR field
- Peaks trace regions where the value of 𝜅 is high → they are associated to massive structures
Multi-scale (wavelet) peak counts
Ajani et. al 2021
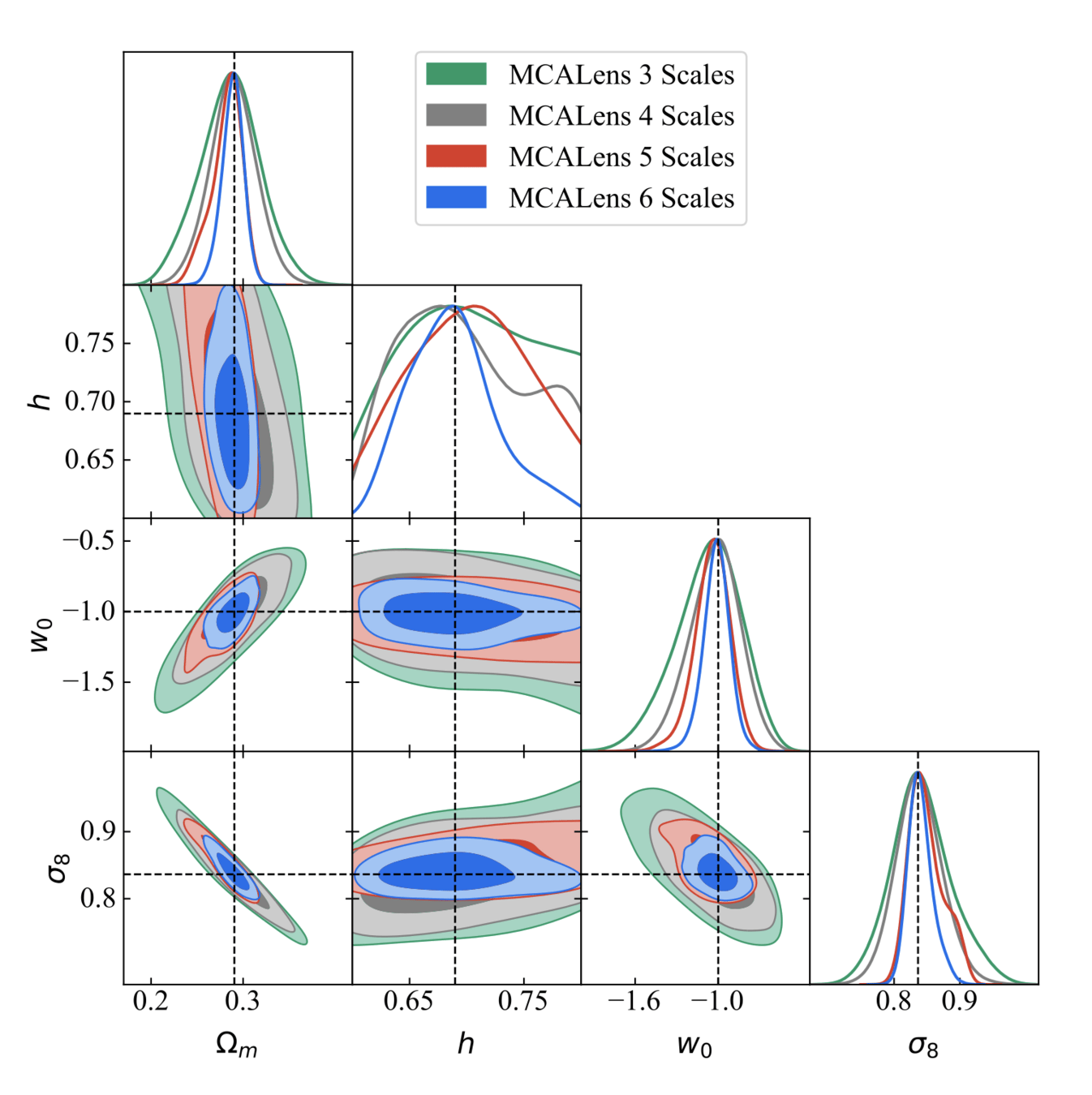
Results
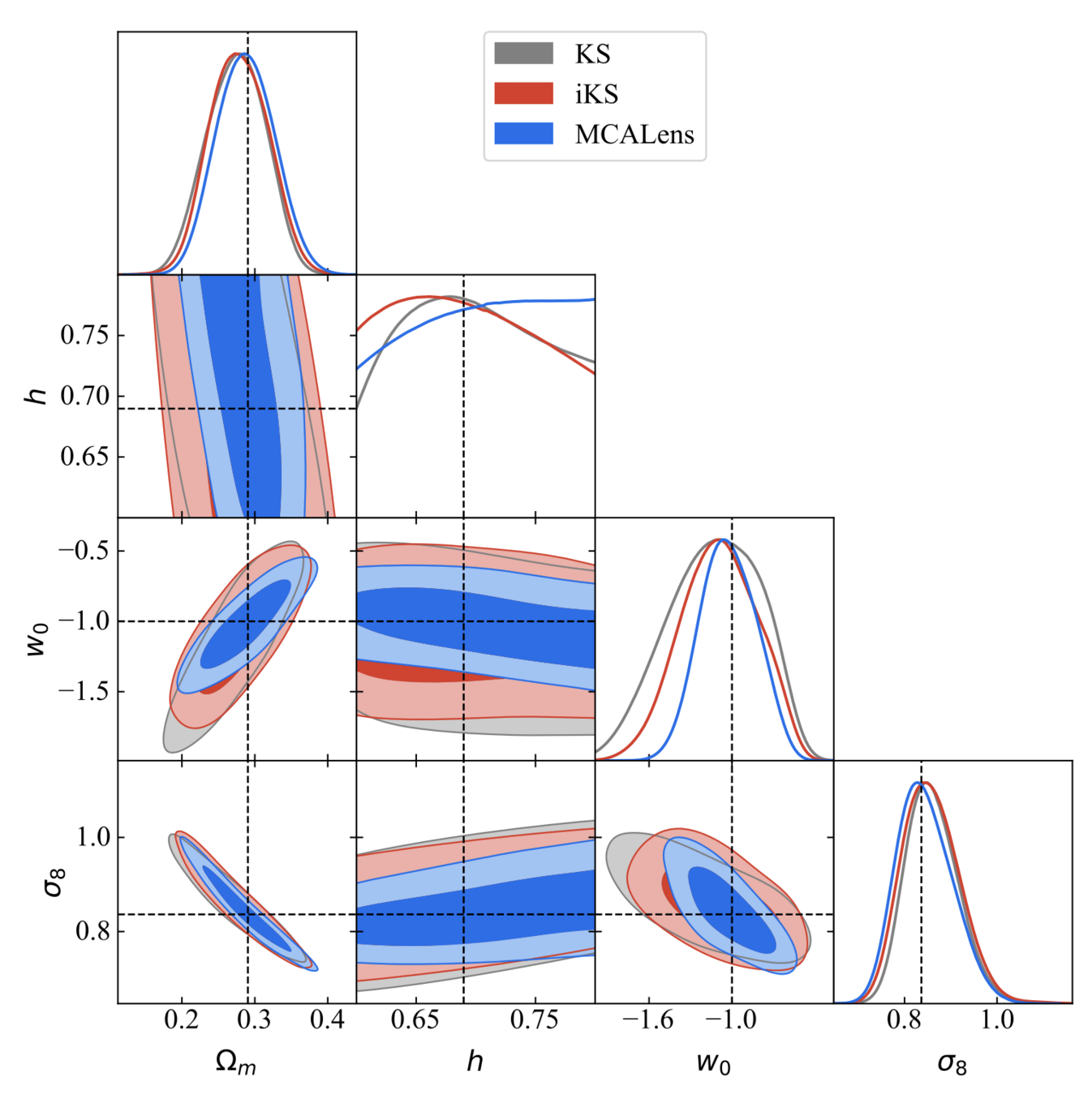
Mono-scale peaks
Multi-scale peaks
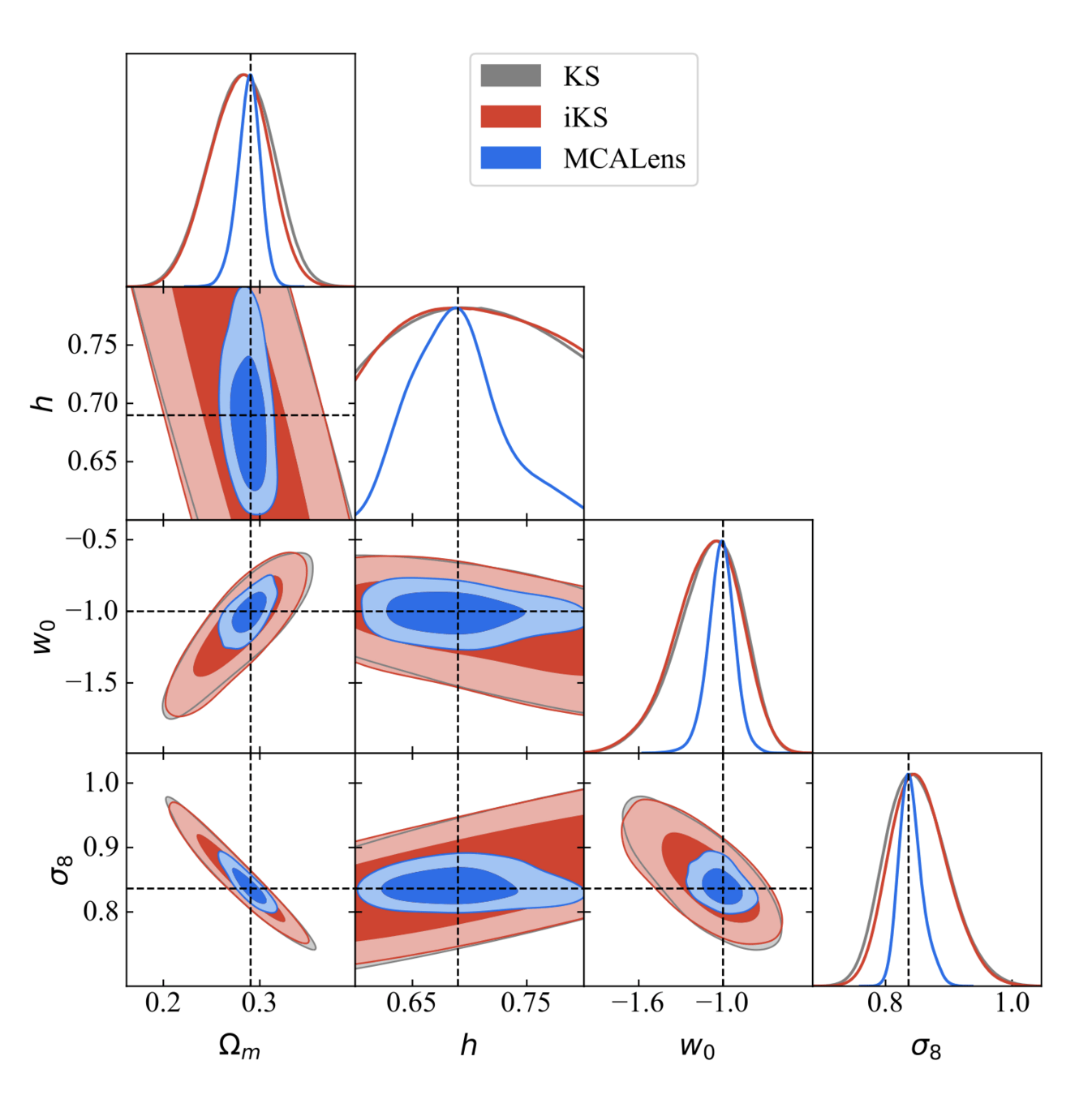
Where does this improvement come from?
Kaiser-Squires
MCALens
Part 2
Impact of baryonic effects on cosmology inference with HOS
with Jean-Luc Starck, Martin Kilbinger & Francois Lanusse
Baryonic effects
- Effects that stem from astrophysical processes involving ordinary matter (gas cooling, star formation, AGN feedback)
-
They modify the matter distribution by redistributing gas and stars within halos.
-
Suppress matter clustering on small scales
- Depend on the cosmic baryon fraction and cosmological parameters.
-
Must be modeled/marginalized over to avoid biases in cosmological inferences from WL.
Baryonic impact on LSS statistics
baryonic effects in P(k)
Credit: Giovanni Aricò
Testing impact of baryonic effects on WL HOS
Idea - Explore two things:
- Information content of summary statistics as a function of scale cuts
- Testing the impact of baryonic effects on posterior contours
This will show:
- On what range of scales can the different statistics be used without explicit model for baryons
- Answer the question: how much extra information beyond the PS these statistics can access in practice
cosmoGRID simulations:
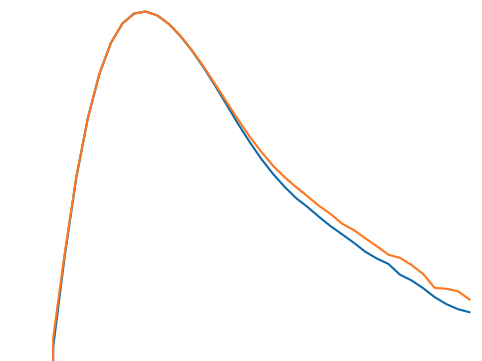
Power Spectrum
Wavelet l1-norm: sum
of wavelet coefficients
within specific amplitude
ranges across different
wavelet scales
Wavelet peaks: local maxima of wavelet
coefficient maps
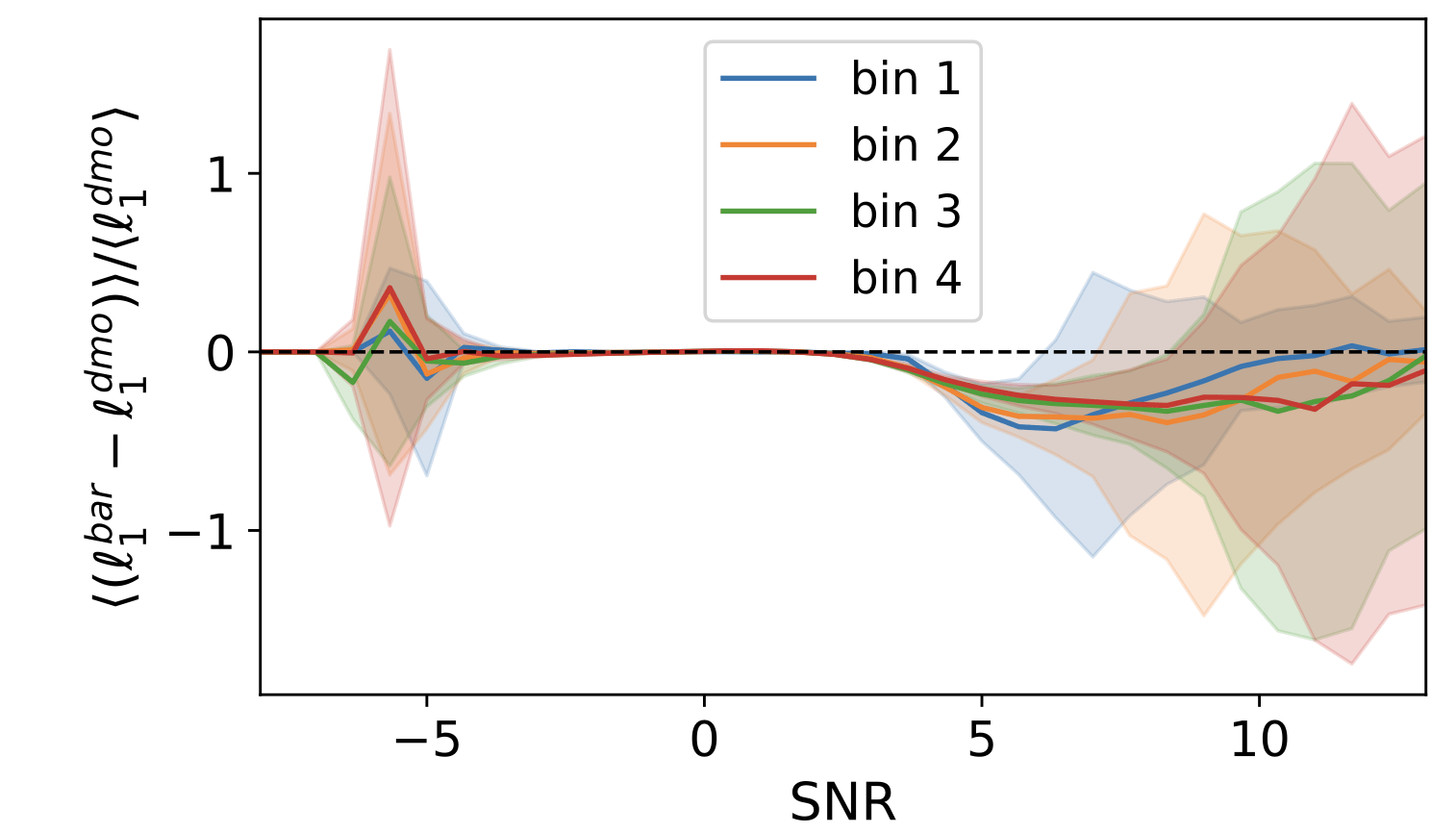
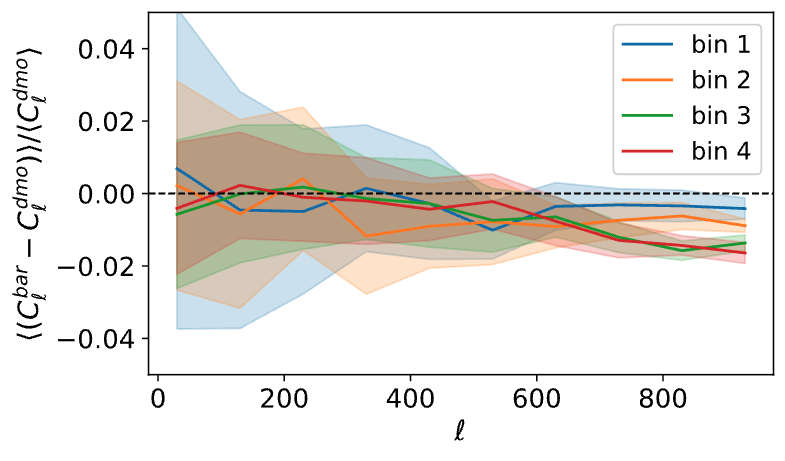
N-body sims, providing DMO and baryonified full-sky κ-maps from the same IC, for 2500 cosmologies. Baryonic effects are incorporated using a shell-based Baryon Correction Model (Schneider et. al 2019).
Inference method: SBI
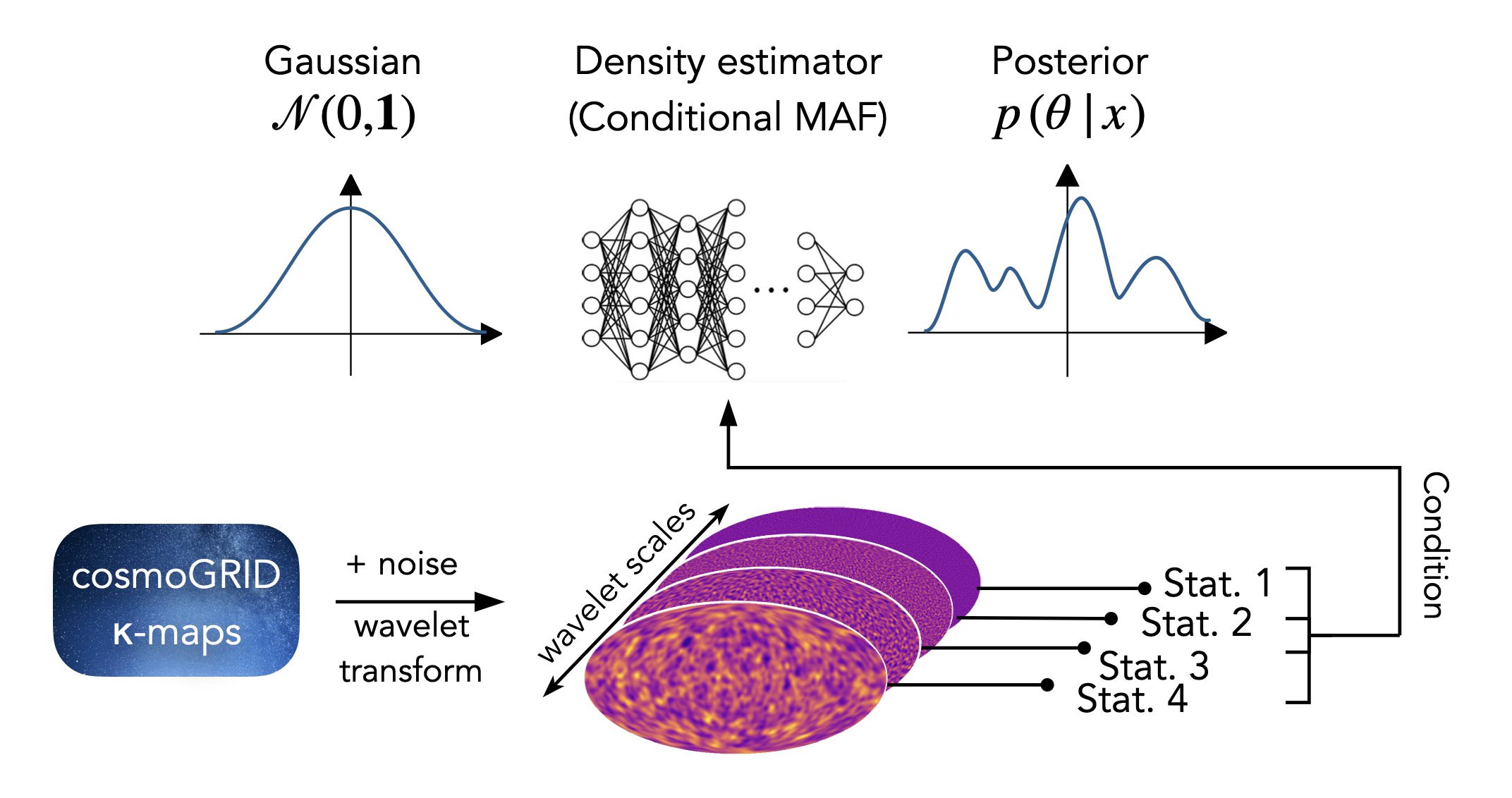
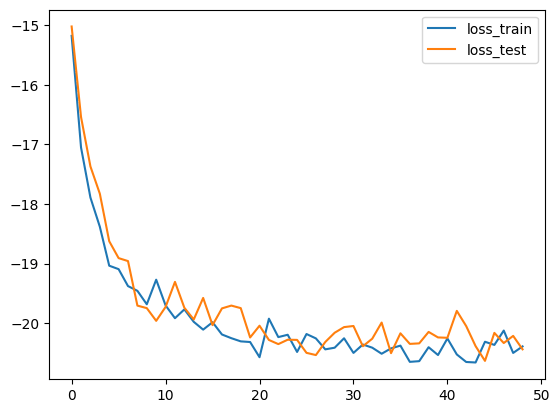
Training objective
\mathcal{L} = - \log p_\phi ( \theta | x )
*
*
Comparison of stats in no-baryons scenario (scale: ~10arcmin)
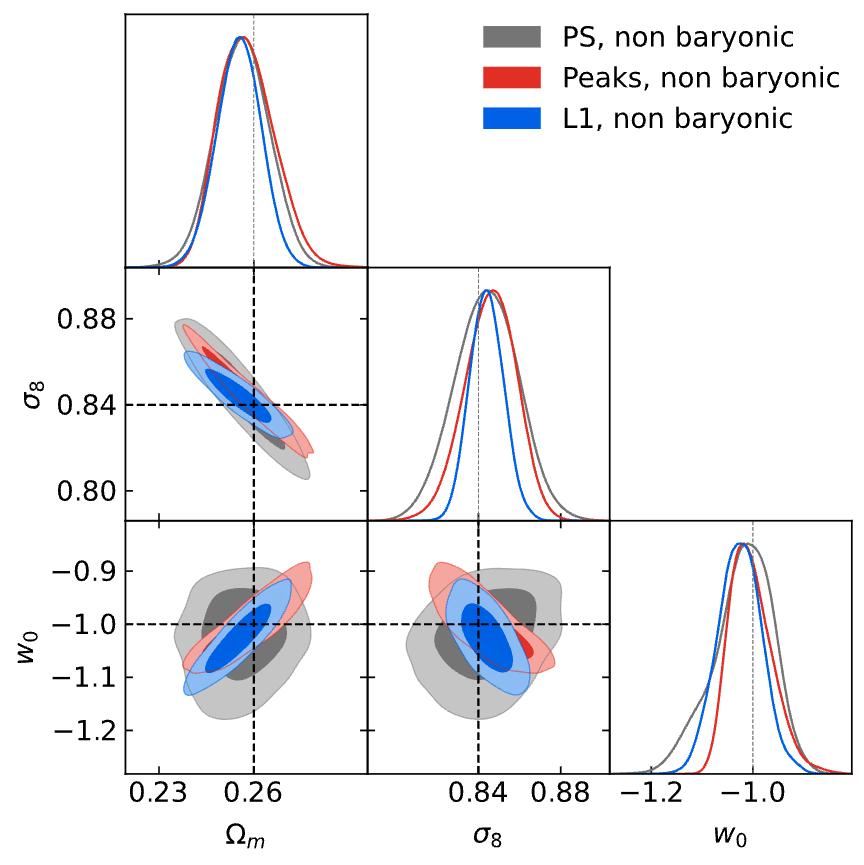
| Statistic | FoM |
|---|---|
| PS | 102 |
| Peaks | 227 |
| l1-norm | 353 |
\mathrm{FoM} \propto \dfrac{1}{\sqrt{ \det (\mathbf{C}_{\rm marg} )}}
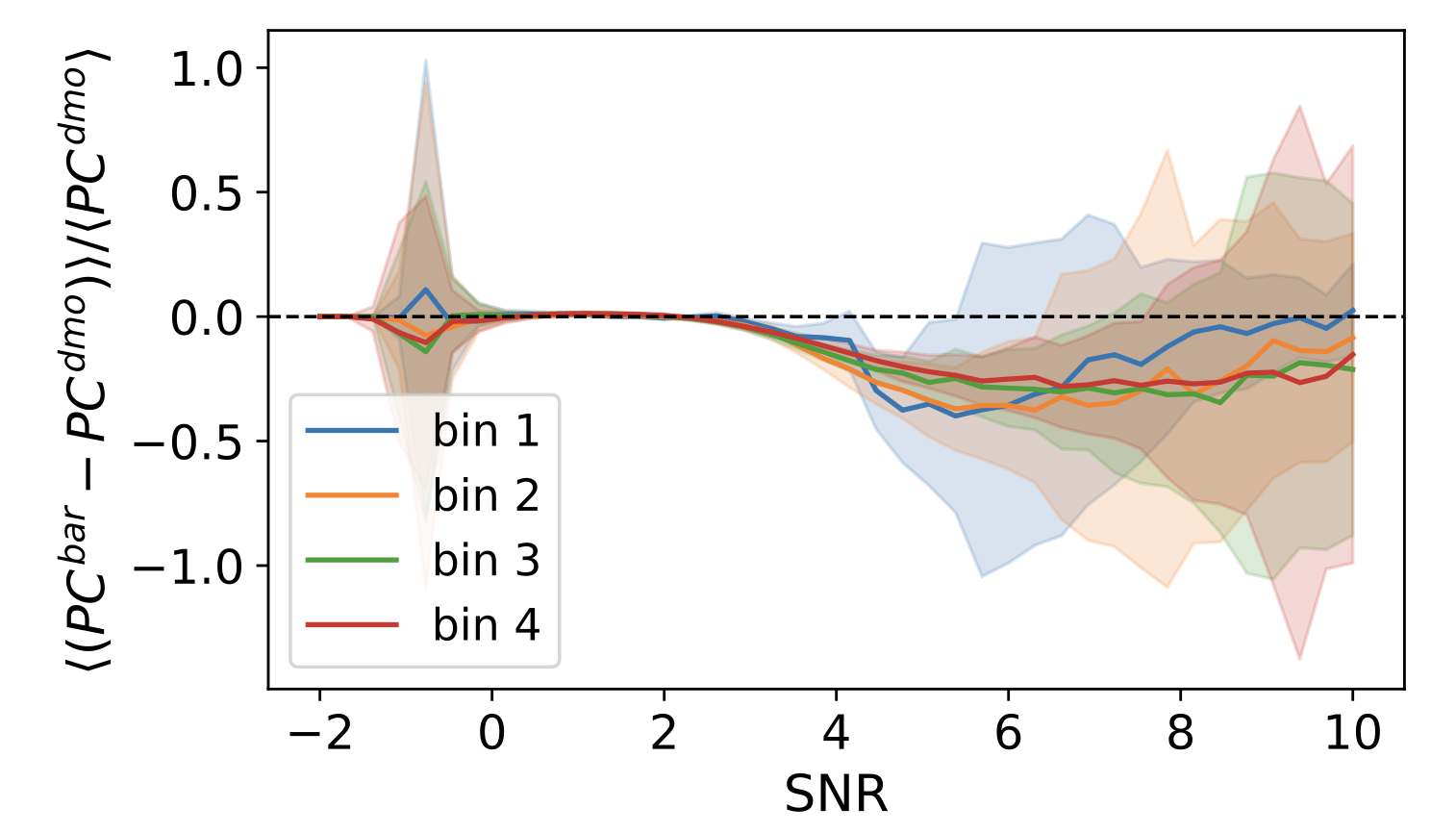
What about the baryonic effects? Do we have any bias?
θ~10arcmin/l=1024
θ~20arcmin/l=540
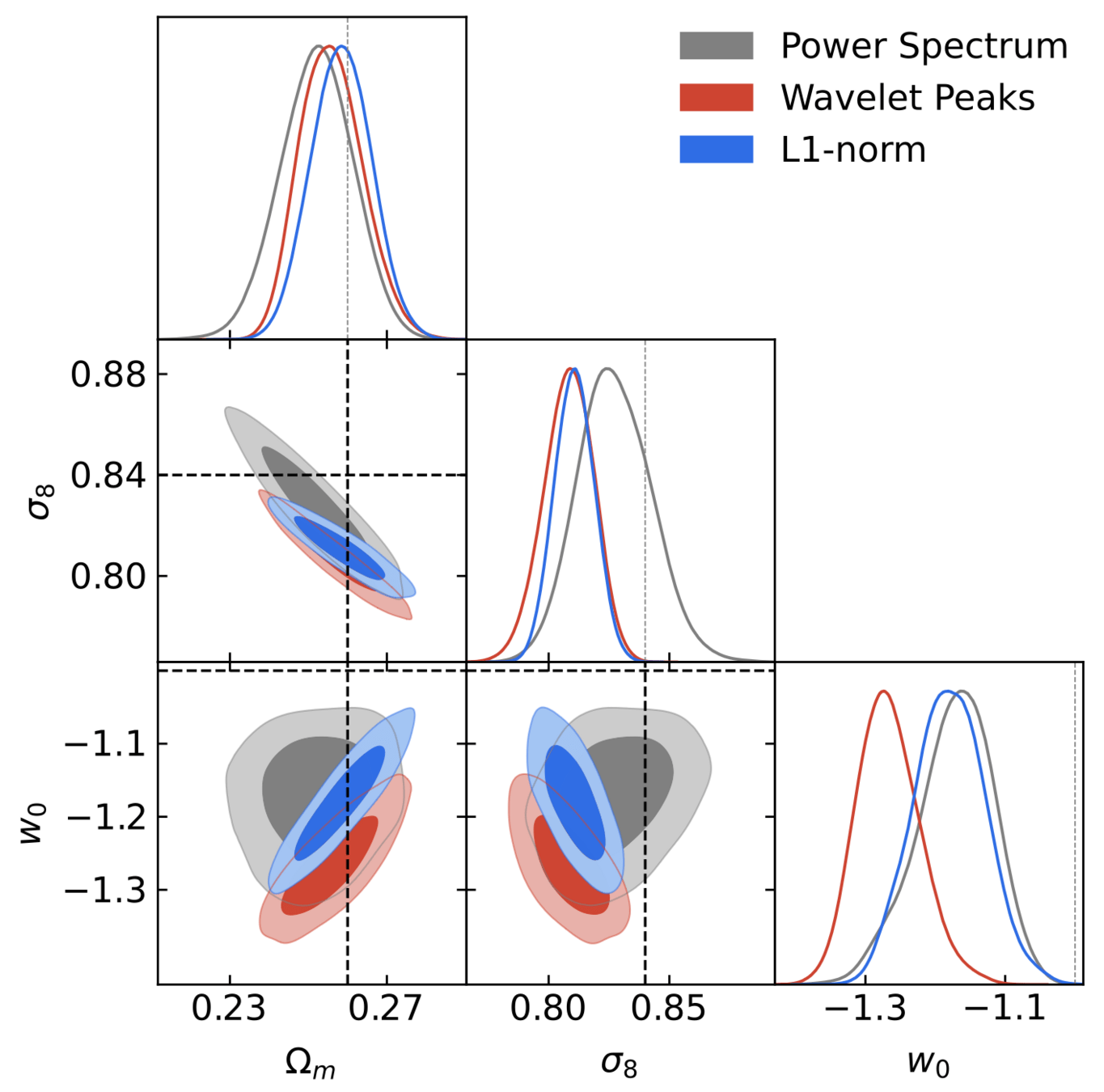
| Statistic | FoM |
|---|---|
| PS | 102 |
| Peaks | 219 |
| l1-norm | 288 |
| Statistic | FoM |
|---|---|
| PS | 53 |
| Peaks | 61 |
| l1-norm | 131 |
| Statistic | FoM(full)/FoM(cuts) |
|---|---|
| PS | 1.9 |
| Peaks | 3.6 |
| l1-norm | 2.2 |
Zu ̈rcher+ (2023)
Weak lensing tomography
Weak lensing tomography
Weak lensing tomography
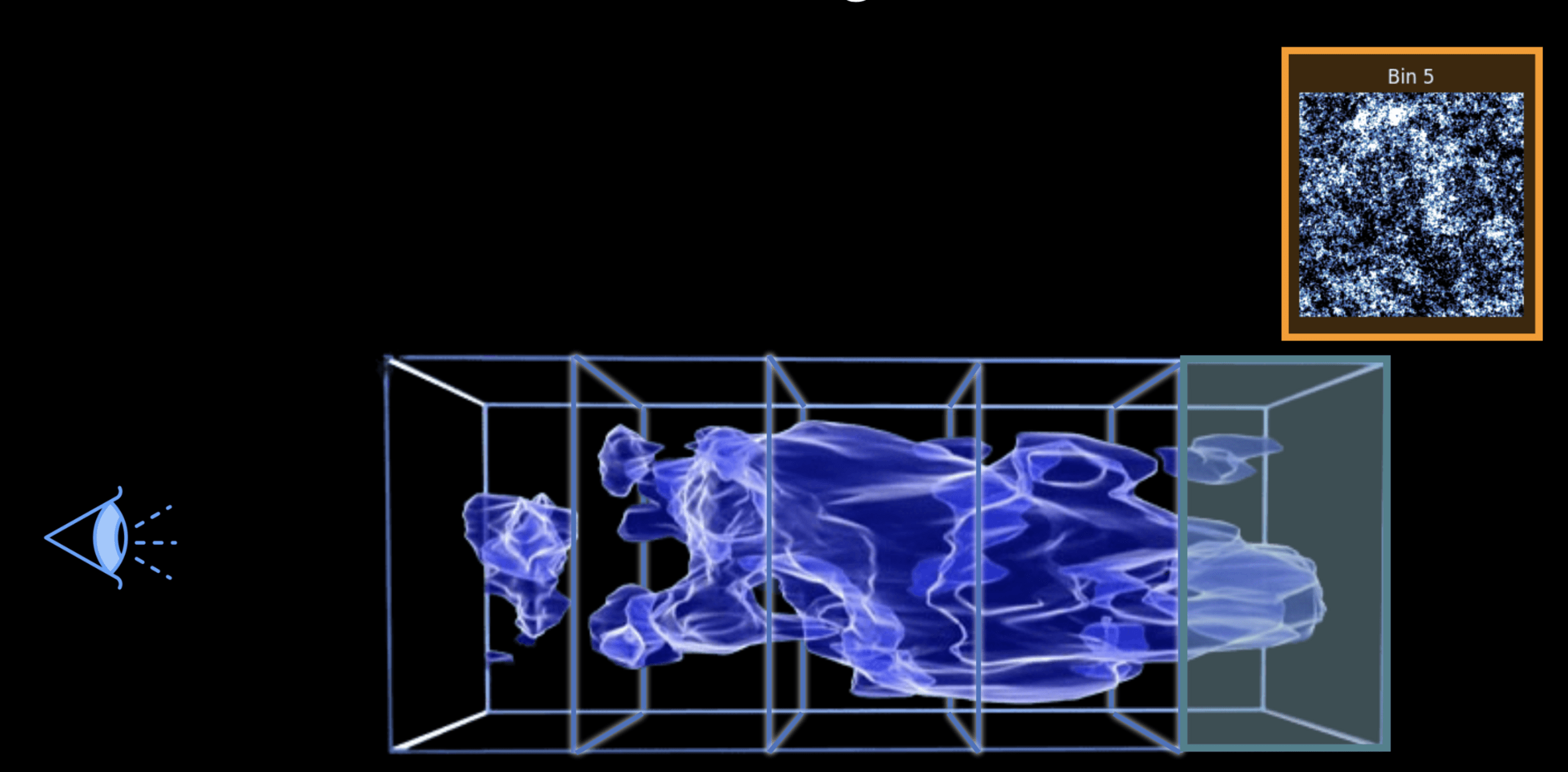
Weak lensing tomography
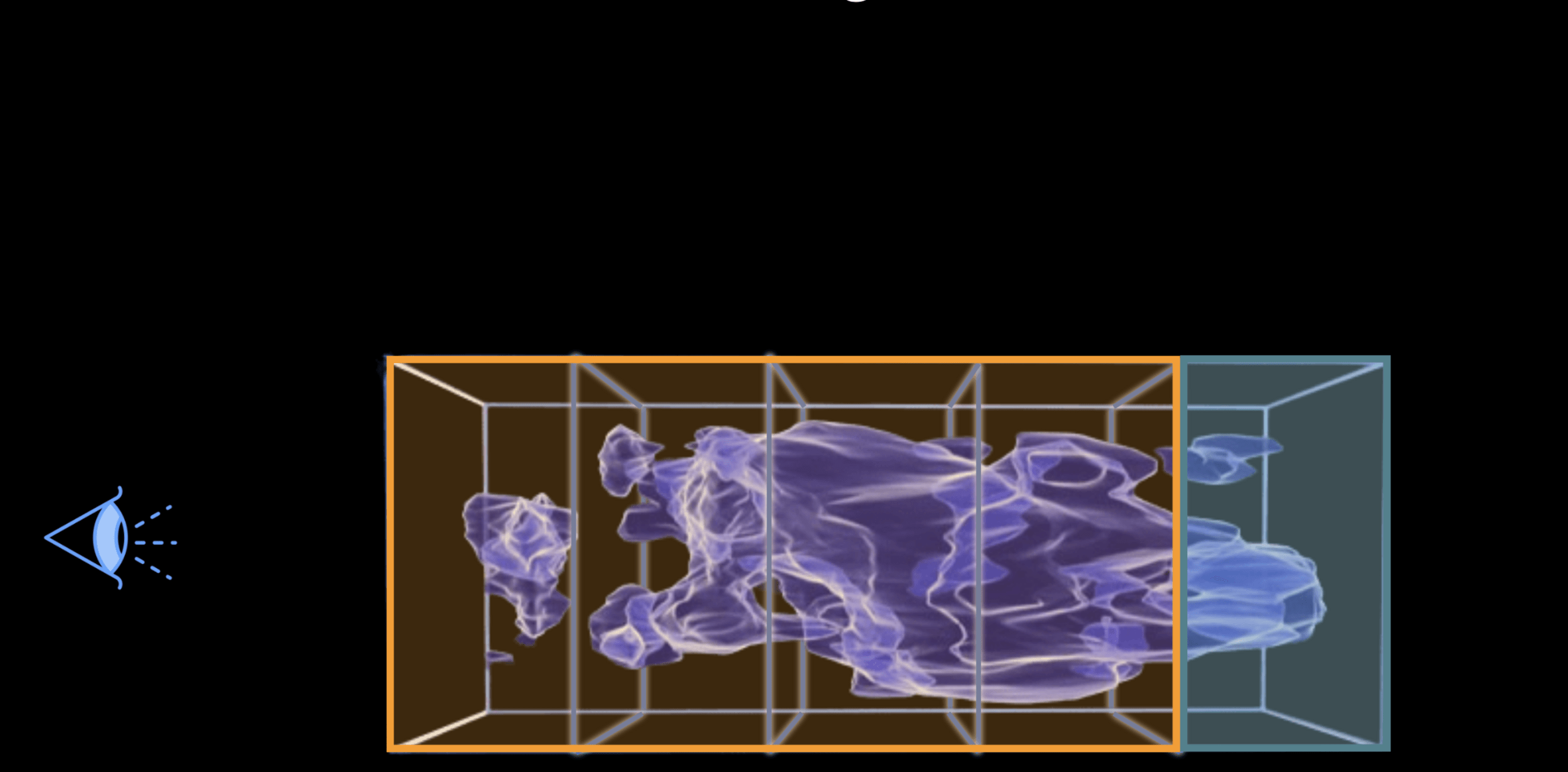
Weak lensing tomography
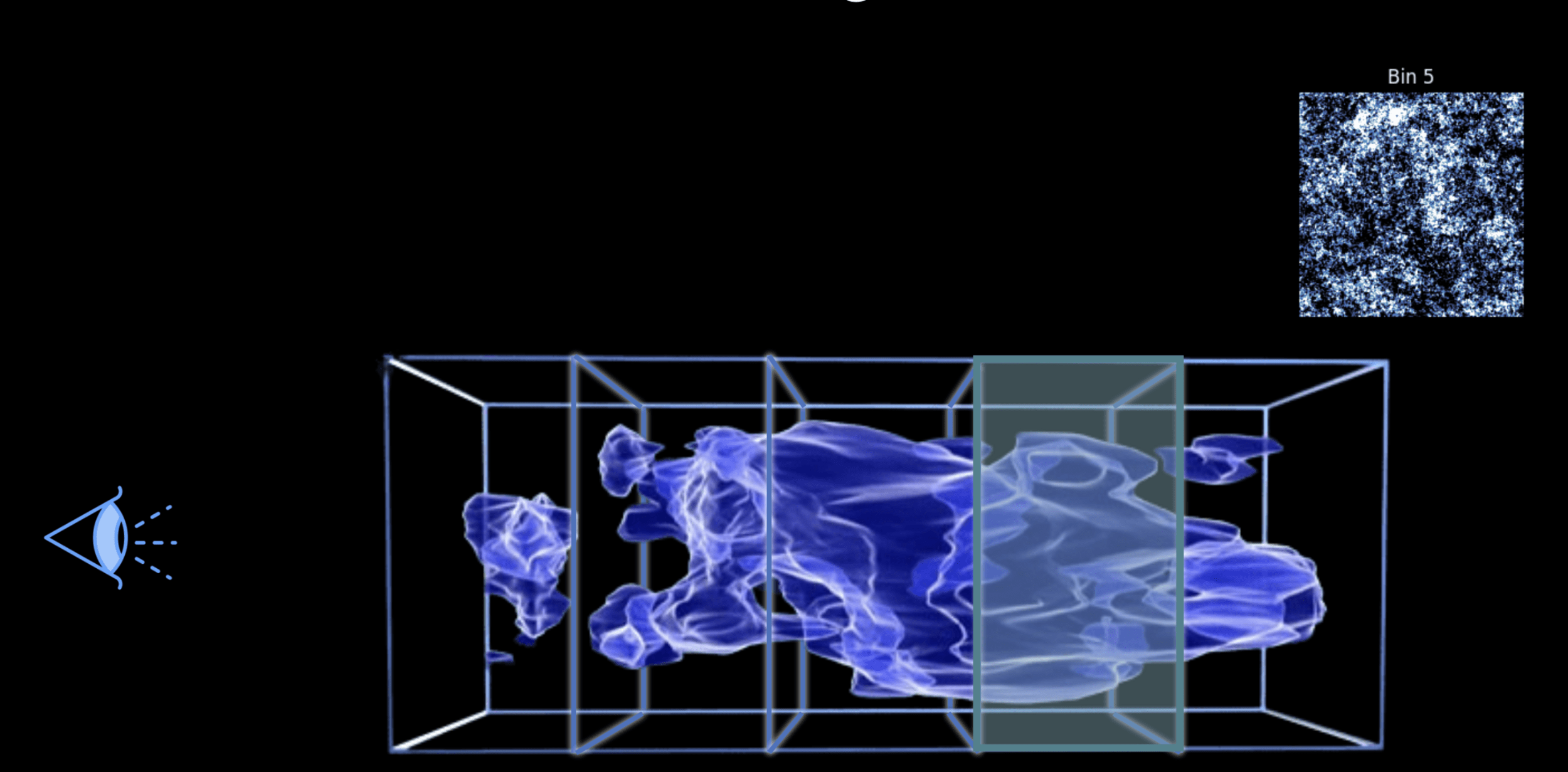
Weak lensing tomography
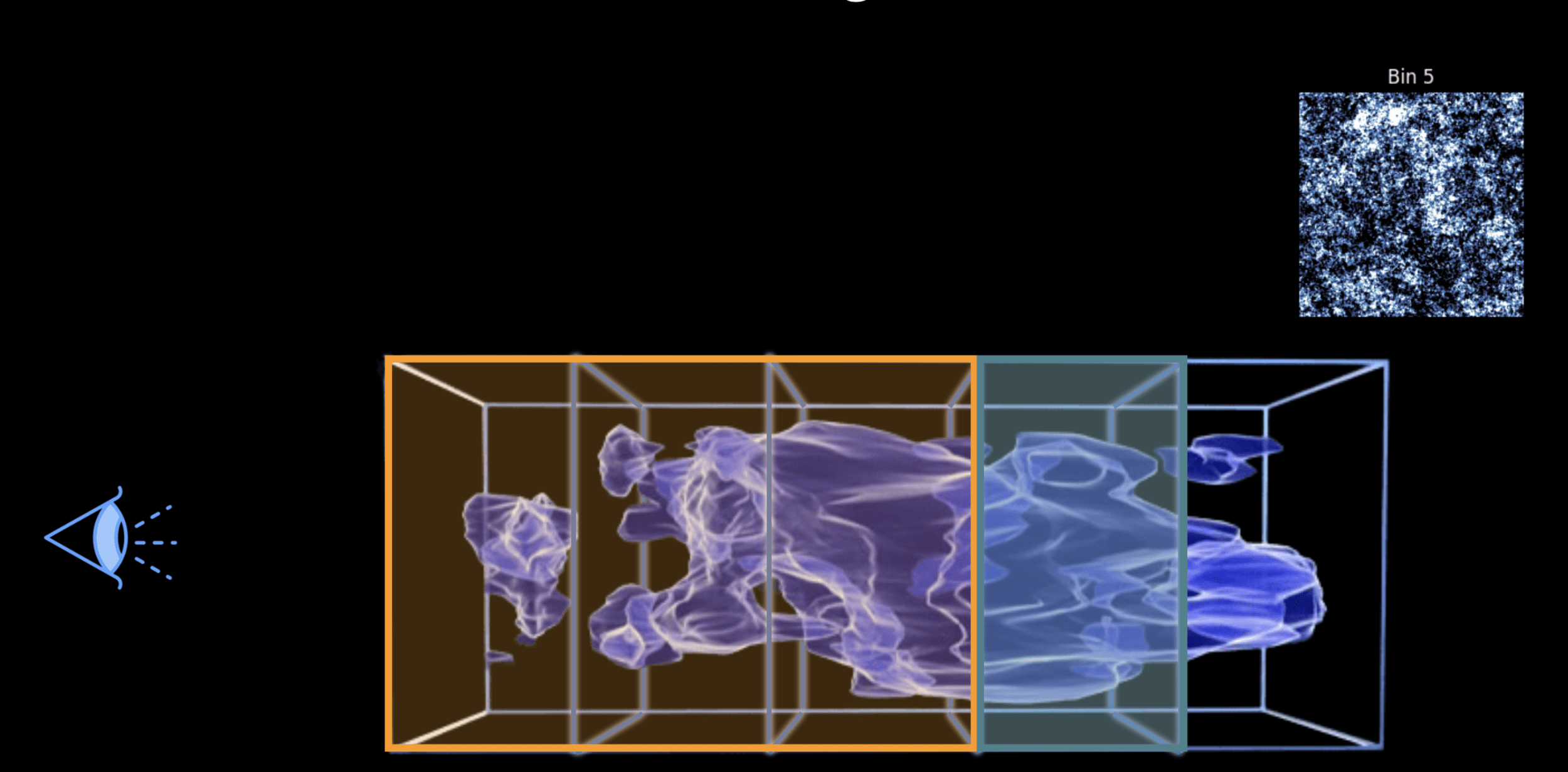
Weak lensing tomography
Weak lensing tomography
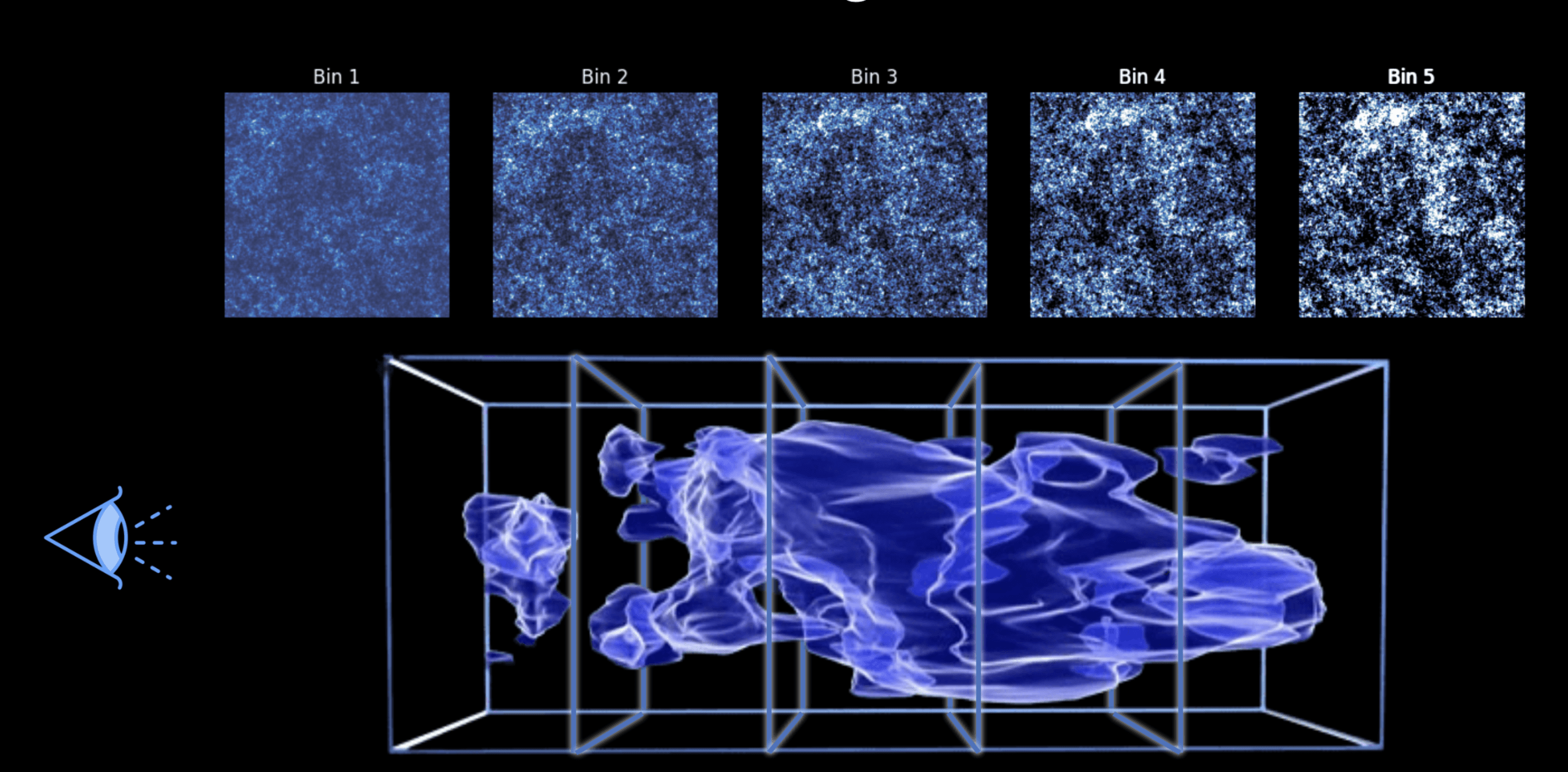
Weak lensing tomography
BNT transform
- When we observe shear, contributions come from mass at different redshifts.
- BNT Transform: method to “null” contributions from unwanted redshift ranges.
- It reorganizes weak-lensing data so that only specific redshift ranges contribute to the signal.
- BNT aligns angular (ℓ) and physical (k) scales.
- This could help mitigate baryonic effects by optimally removing sensitivity to poorly modeled small scales and controlling scale leakage.
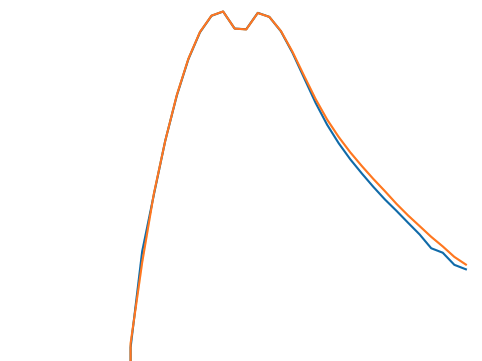
BNT maps
no BNT
BNT
How are statistics impacted?
Power Spectrum
l1-norm
* This could help mitigate baryonic effects by optimally removing sensitivity to poorly modeled small scales and controlling scale leakage?
How about contours?
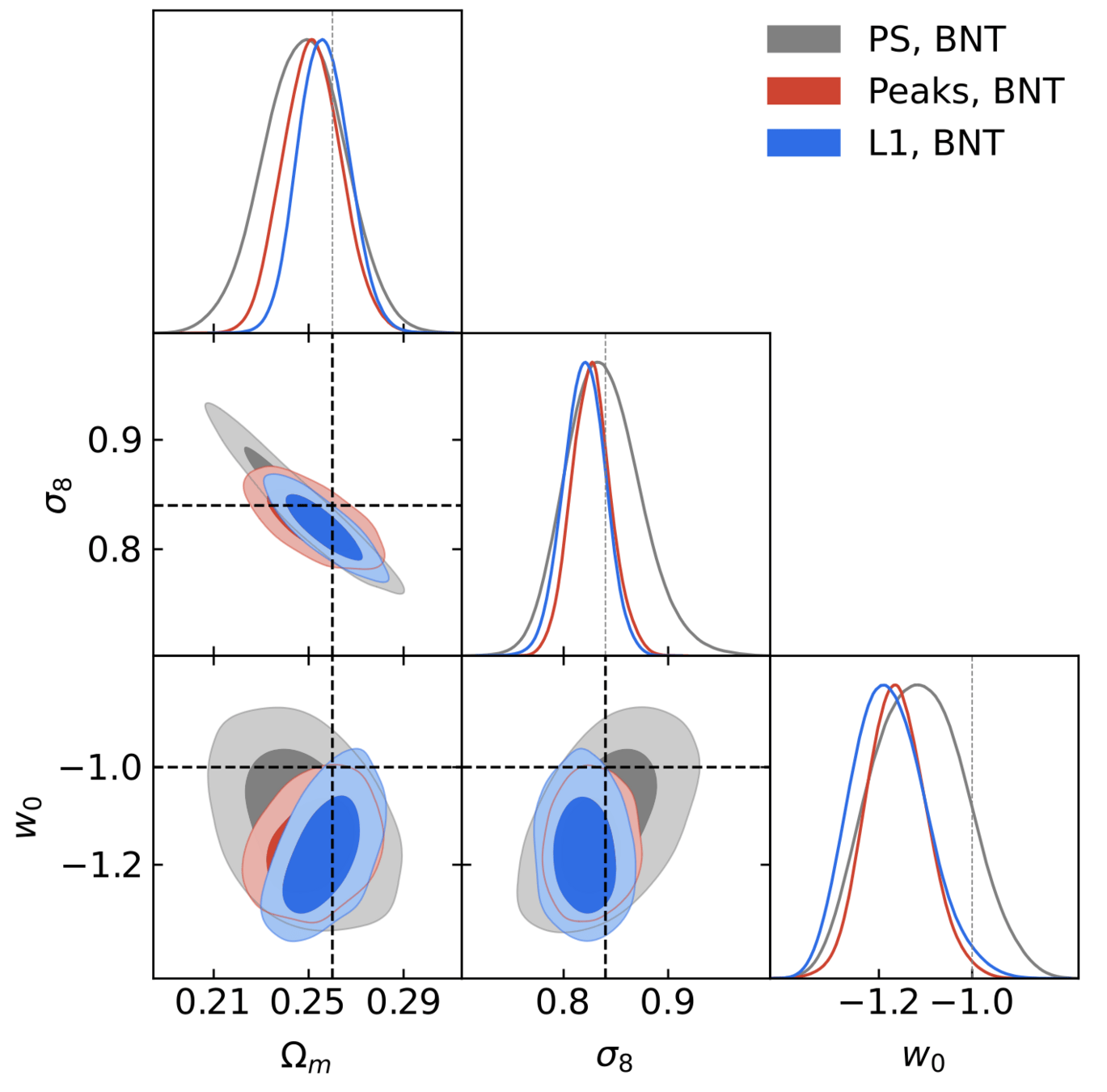
| Statistic | FoM |
|---|---|
| PS | 8 |
| Peaks | 10 |
| l1-norm | 19 |
| Statistic | Factor |
|---|---|
| PS | 12.6 |
| Peaks | 22.9 |
| l1-norm | 15.3 |
Loss of power compared to contours without cuts
| Statistic | Factor |
|---|---|
| PS | 6.6 |
| Peaks | 6.3 |
| l1-norm | 7.0 |
Loss of power compared to contours with cuts
Conclusions
Part 2
- Unmodeled baryonic effects can lead to significant bias in cosmological parameters.
- To remove the bias from baryons, stringent scale cuts are required (ℓ~500 ).
- Even after scale cut at ℓ~500, HOS maintain significantly increased constraining power, compared to the PS.
- The BNT transform, while offering more physical scale cuts, leads to a significant inflation in contour size.
Part 1
- Mass mapping can have a significant impact on cosmological contours
- With a state-of-the-art mass-mapping method (MCALens) we managed to get 2.6x improvement in FoM over KS.
Hope: Neural Summaries (VMIM)
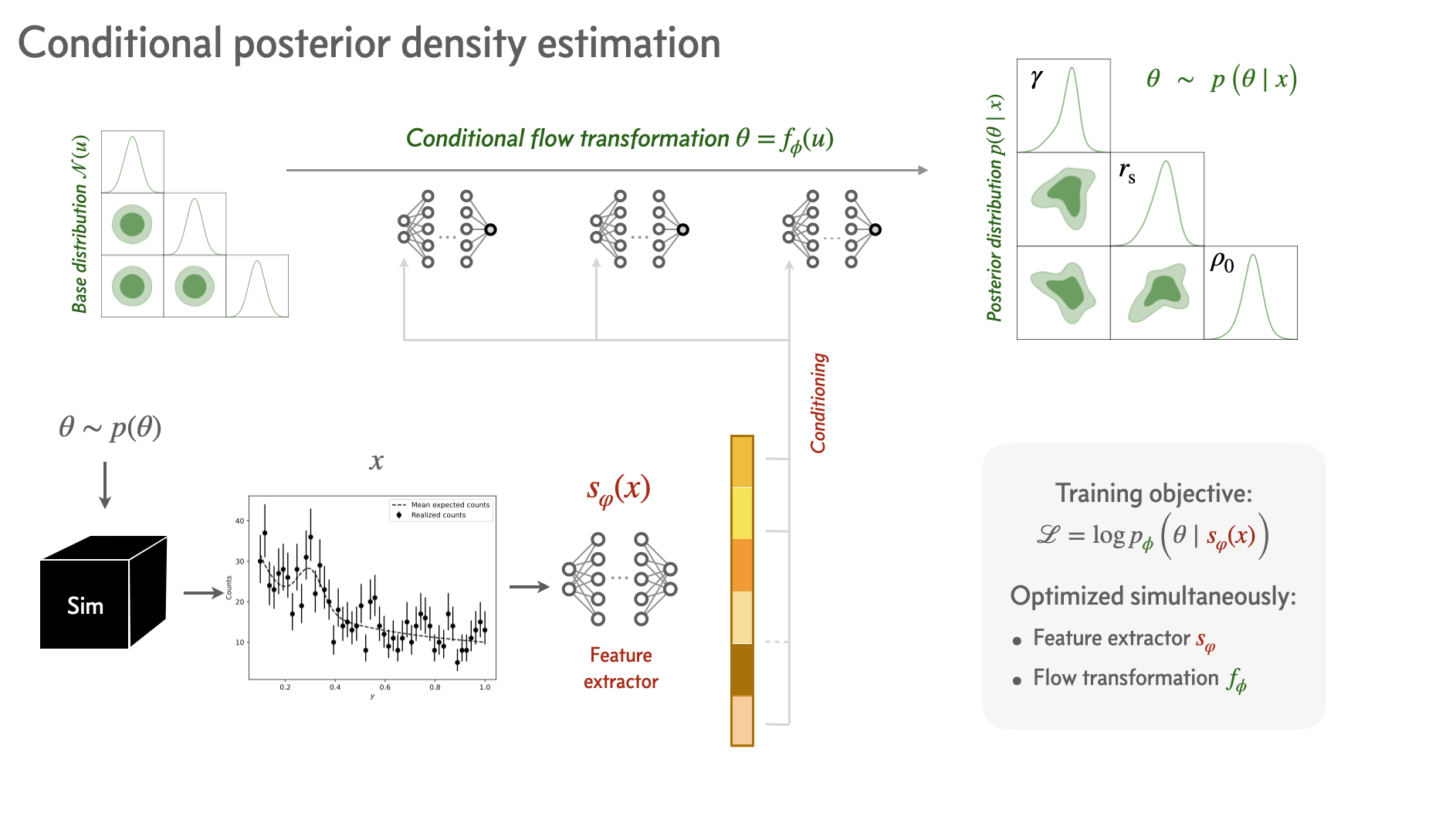
Hope: Neural Summaries (VMIM)
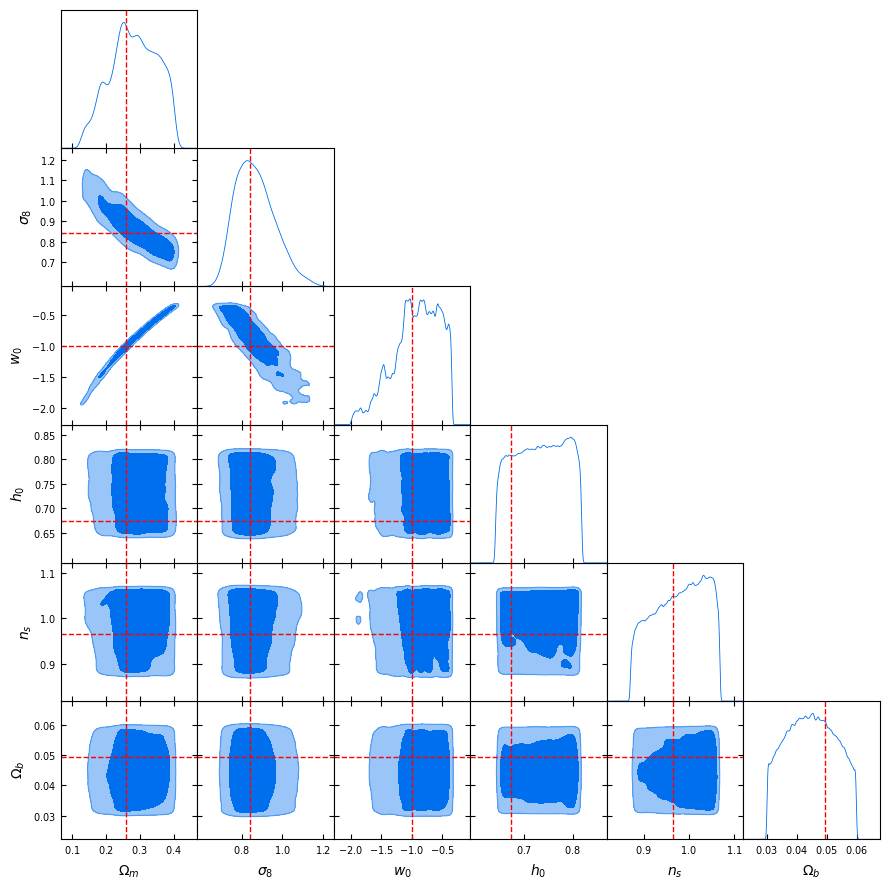
Euclid Meeting, Marseille, September 25, 2025
By Andreas Tersenov
