Quantum spin liquid in \(\text{Ba}_4\text{Ir}_3\text{O}_{10}\)?
What's a quantum spin liquid?
- Conventional magnets
Order at low temperatures by breaking symmetry, classical product states, short-range entangled
- Quantum spin liquids
Long-range entanglement, do not order due to quantum fluctuations, non-local fractional excitations (spinons)
broken symmetry \(\rightarrow\) collective excitations (magnons)
What's a quantum spin liquid?
Mechanisms:
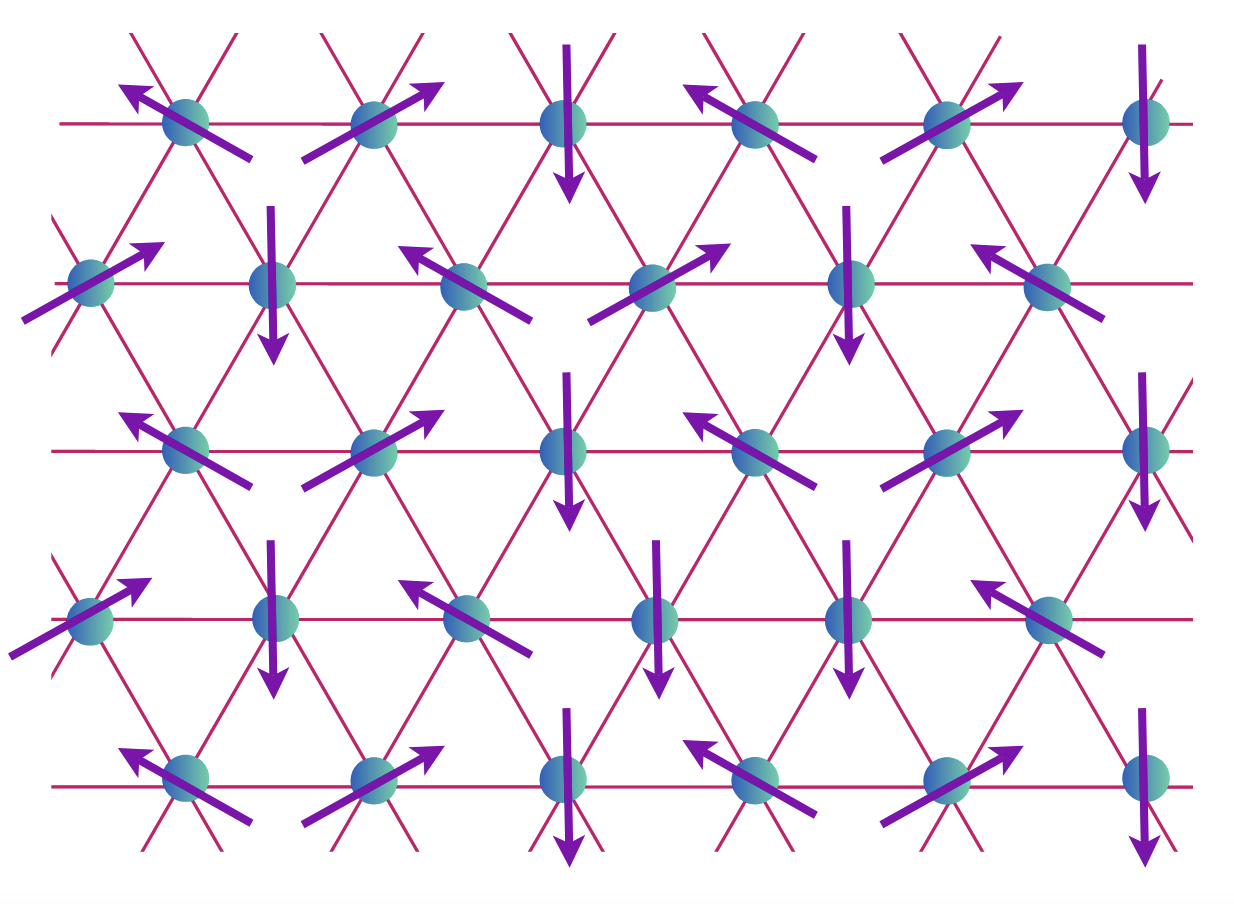
Example: triangular lattice antiferromagnet
ordered state
+
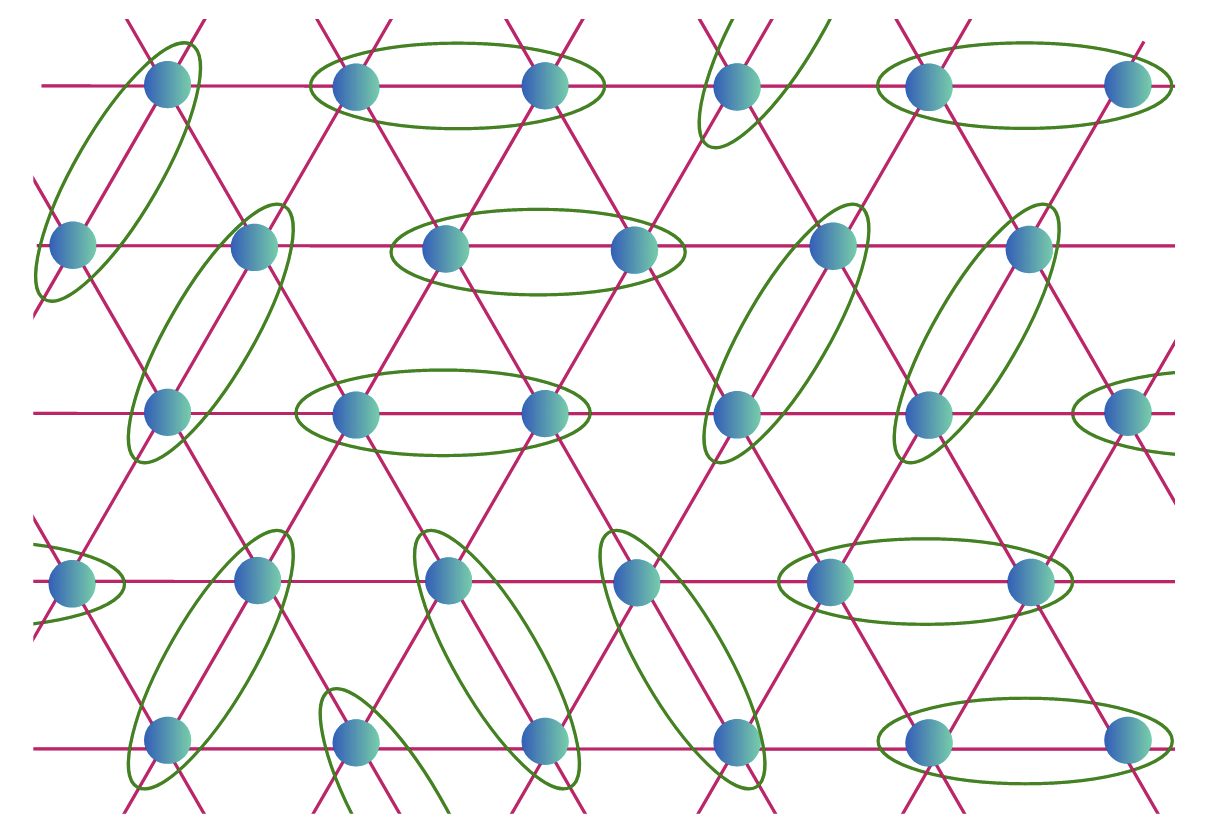
+ \(\dots\)
spin liquid
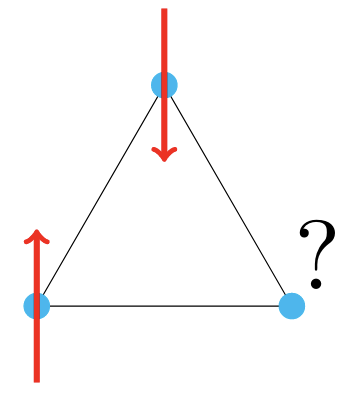
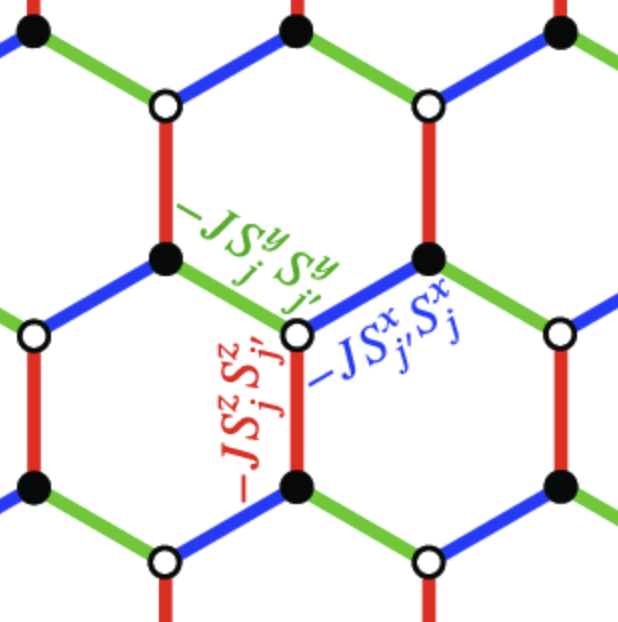
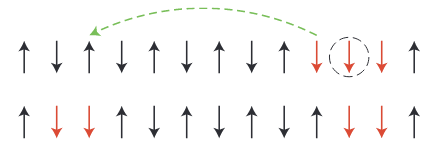
low dimensionality
frustration
Quantum spin liquid in \(\text{Ba}_4\text{Ir}_3\text{O}_{10}\)?
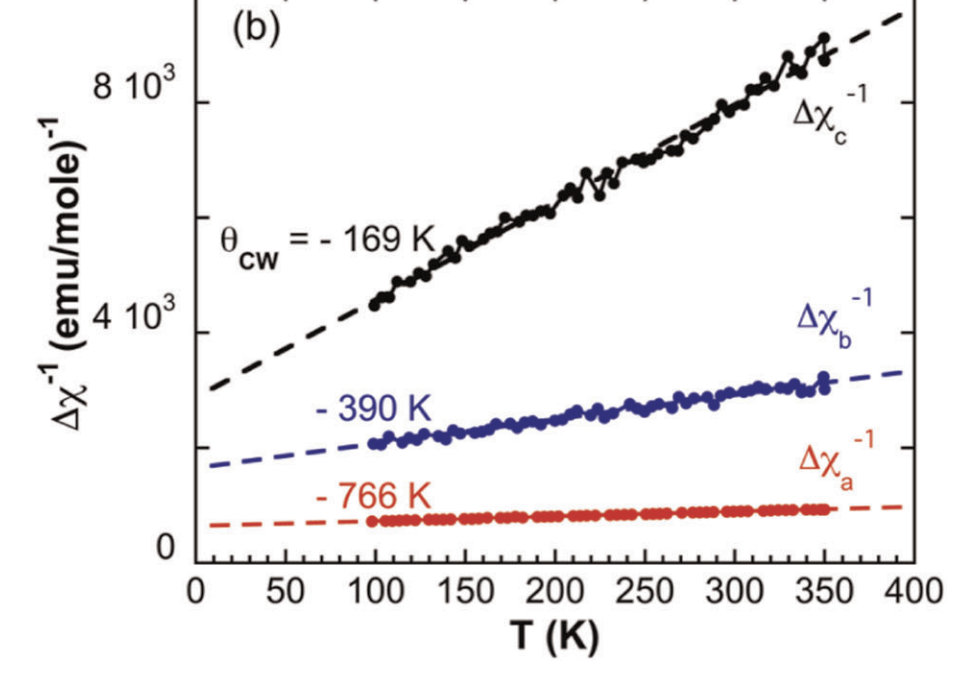
inverse susceptibility
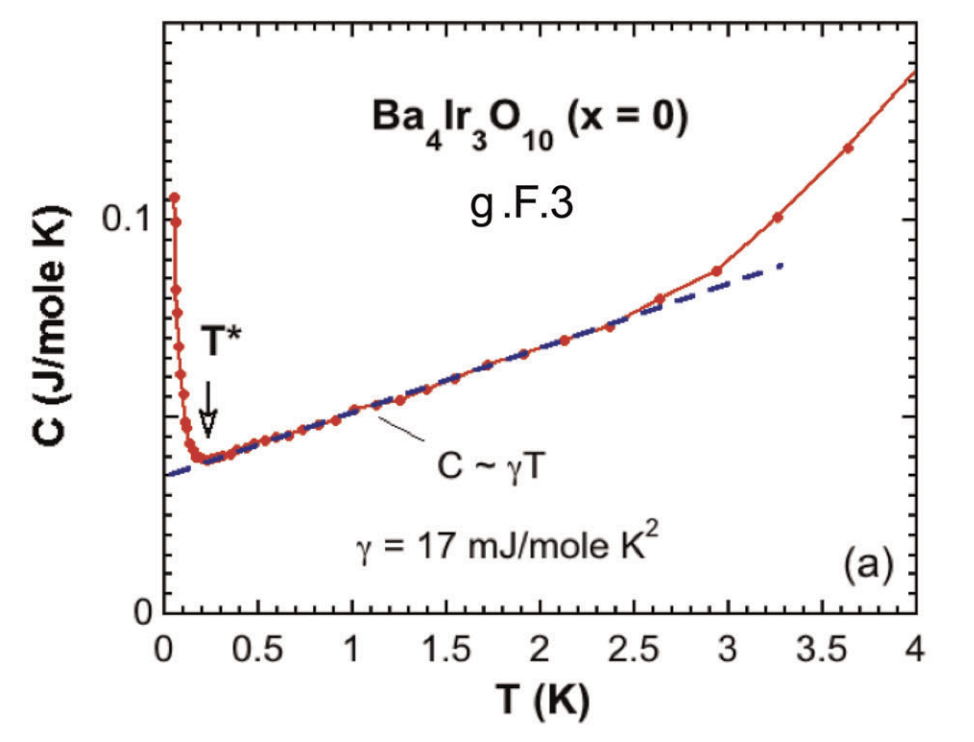
heat capacity
- Insulator with T-linear heat capacity
- Interactions ~ 500 K but orders at 0.2 K
- 2D but not geometrically frustrated
Different descriptions
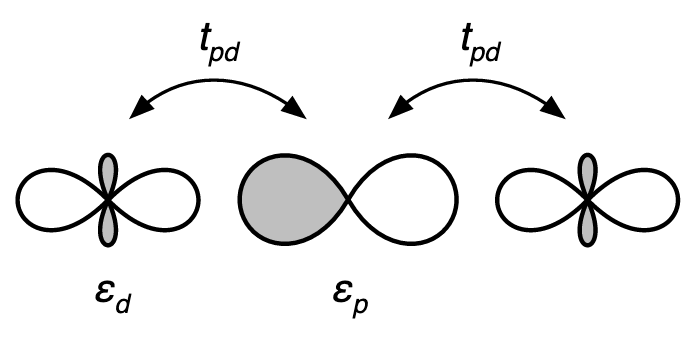
Electron model:
\(H = t_{ij}c_i^{\dagger}c_j +v_{ijkl}c_i^{\dagger}c_j^{\dagger}c_lc_k + \dots\)
Spin model:
\(H = J_{ij}\mathbf{S}_i.\mathbf{S}_j + J_{ijkl}(\mathbf{S}_i.\mathbf{S}_j)(\mathbf{S}_k.\mathbf{S}_l) + \dots \)
Parton theory:
\(H = t_{ij}f_i^{\dagger}A_{ij}f_j + \dots\)
review article: Quantum Spin Liquids, Savary and Balents, 2016
Relevant interactions
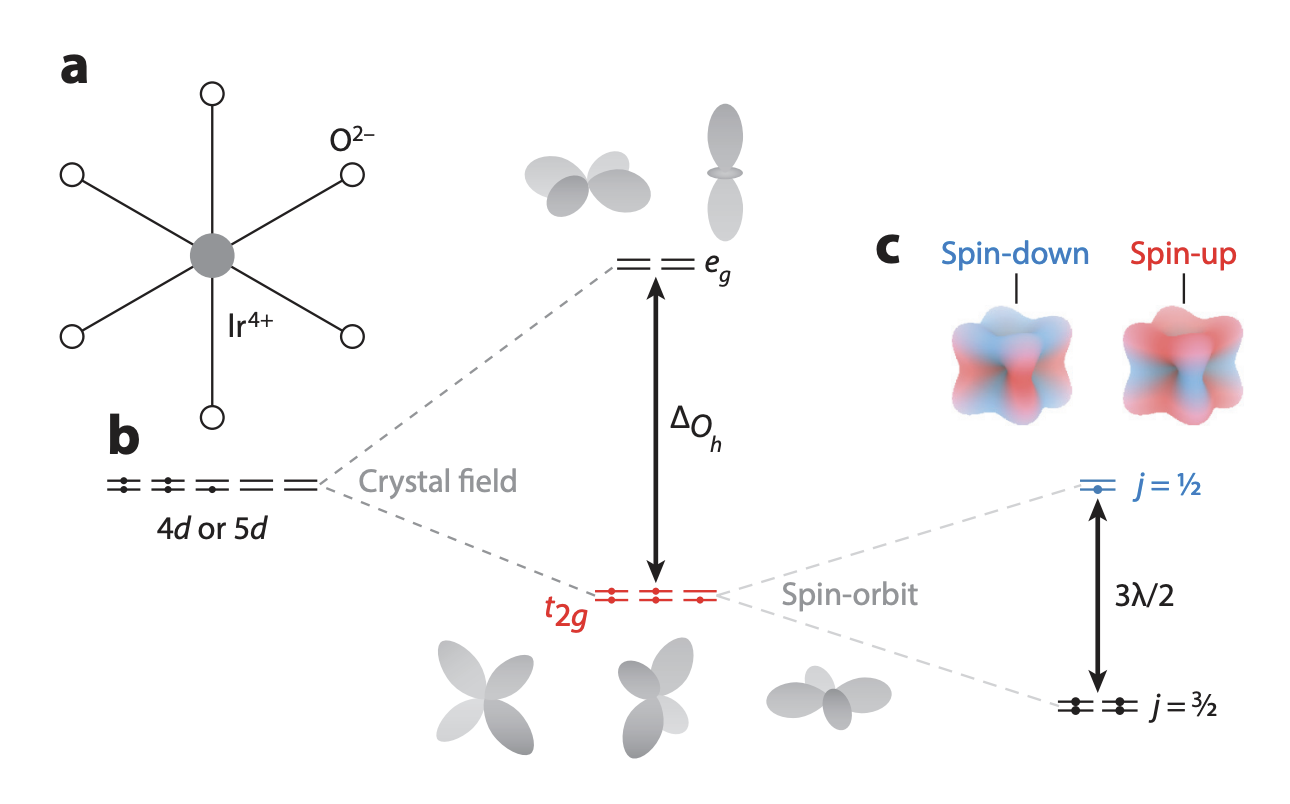
- \(\text{Ir}^{4+}:\ 5d^5\) valence electrons
- crystal field ~ on-site Coulomb repulsion > Hund's coupling \(\geq\) spin-orbit coupling \(\geq\) hopping
Pseudo spin-halfs (?)
Ab initio wave function calculations
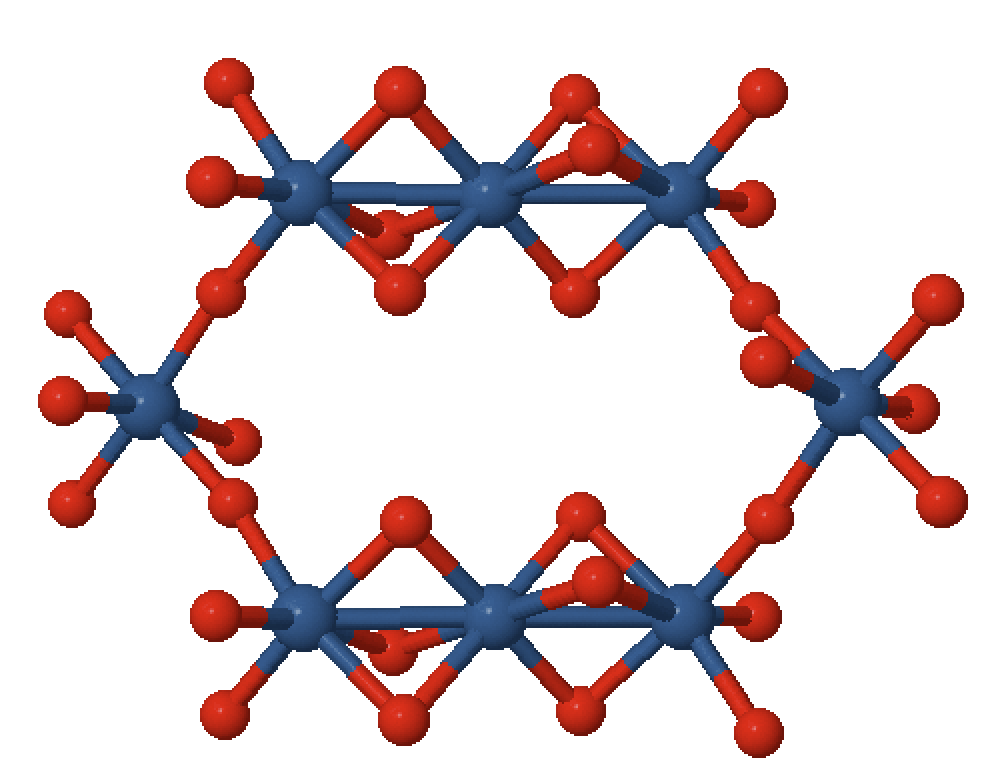
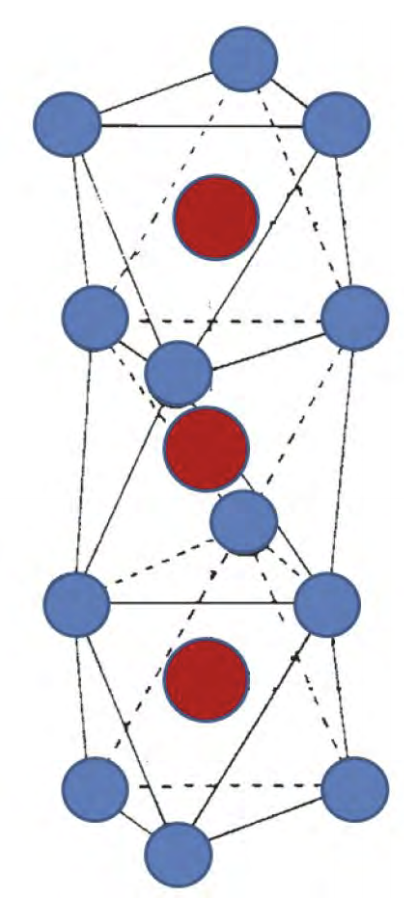
Face shared octahedra
Calculating valence electron wave functions for embedded clusters including all relevant interactions
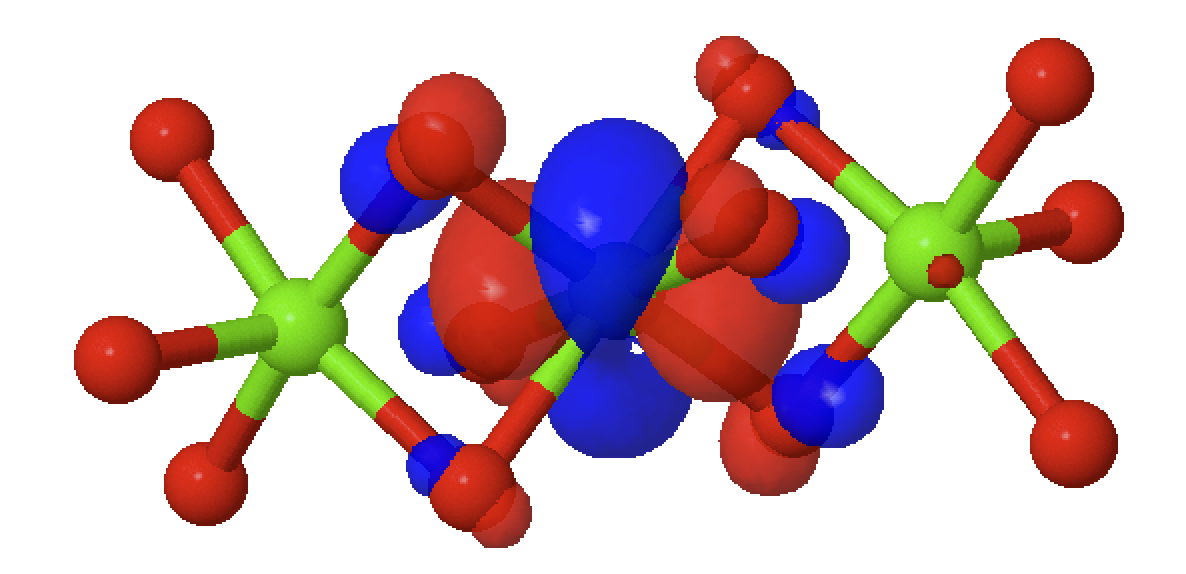
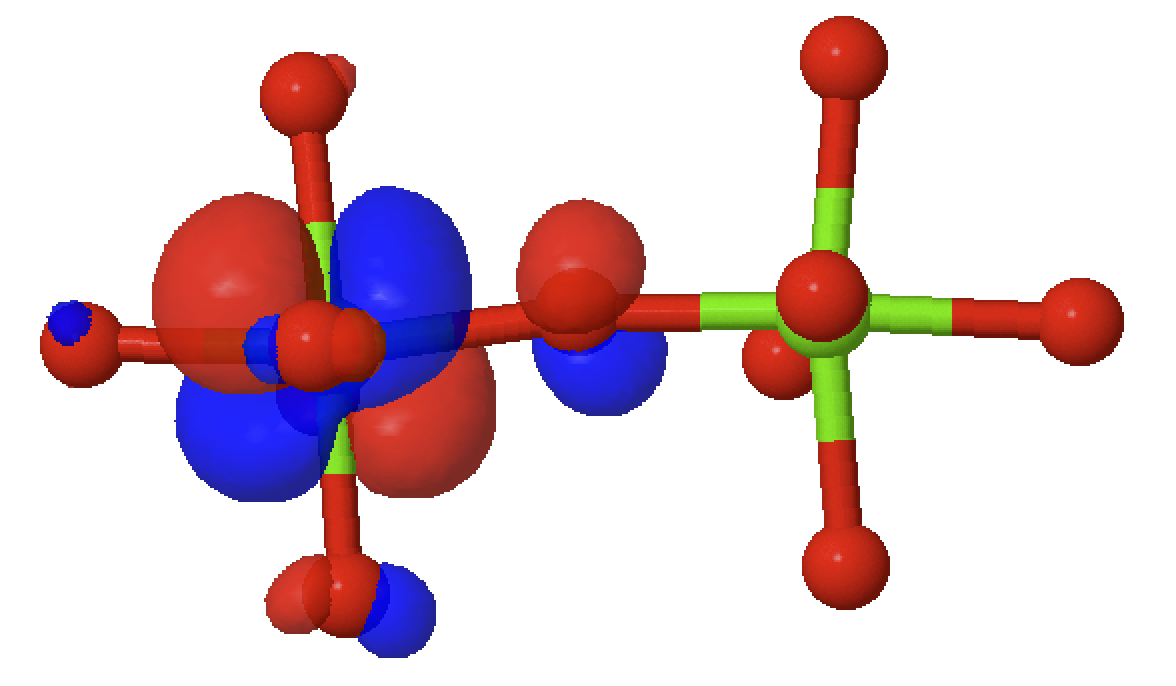
Low lying energy levels:
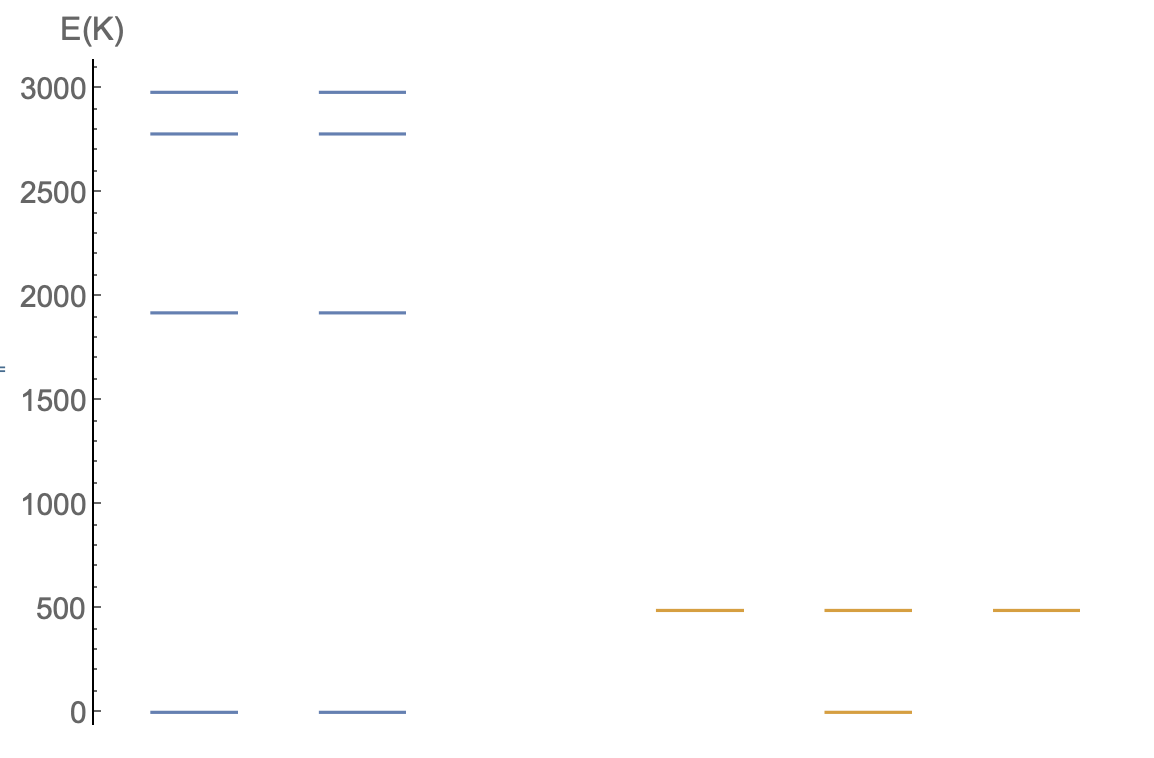
Face shared
Corner shared
Effective hamiltonian: electrons \(\rightarrow\) spins
H = -t\sum_{\langle i, j\rangle,\sigma}c_{i\sigma}^{\dagger}c_{j\sigma} + U\sum_{i}n_{i\uparrow}n_{i\downarrow}
Hubbard model:
Strong coupling limit: \( U \gg t\)
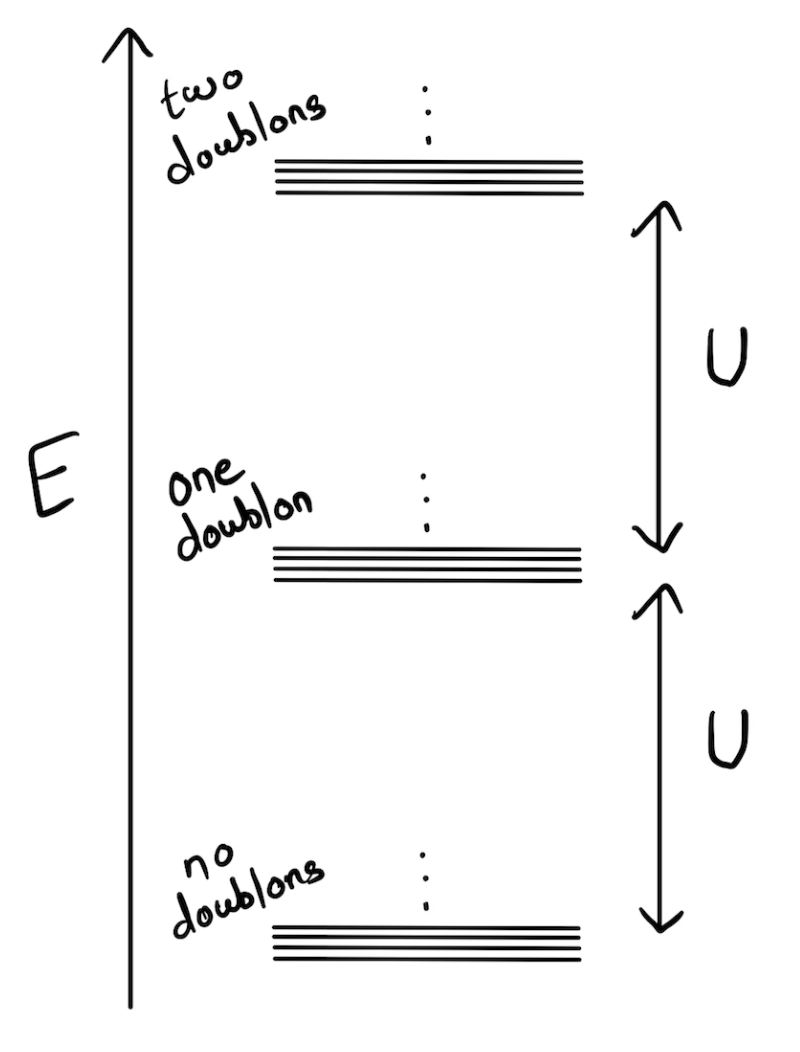
Integrate out high energy doublons
Exchange process
H_{\text{eff}} = J\mathbf{S}_1.\mathbf{S}_2
J \sim t^2/U
At quartic order: next-nearest neighbors, ring exchange (\(\sim t^4/U^3\))
Exchange with SOC
H = -t\sum_{\langle i, j\rangle,\sigma,\sigma'}\tilde{a}_{i\sigma}^{\dagger}\tilde{a}_{j\sigma'} + U\sum_{i}n_{i\uparrow}n_{i\downarrow}
Pseudospin flips allowed!
H_{\text{eff}}= \mathbf{S}_1.R^{T}JR.\mathbf{S}_2
=J\cos\phi\mathbf{S}_1.\mathbf{S}_2 + (1-\cos\phi)(\hat{\mathbf{d}}.\mathbf{S}_1)(\hat{\mathbf{d}}.\mathbf{S}_2) + \sin\phi\hat{\mathbf{d}}.(\mathbf{S}_1\times\mathbf{S}_2)
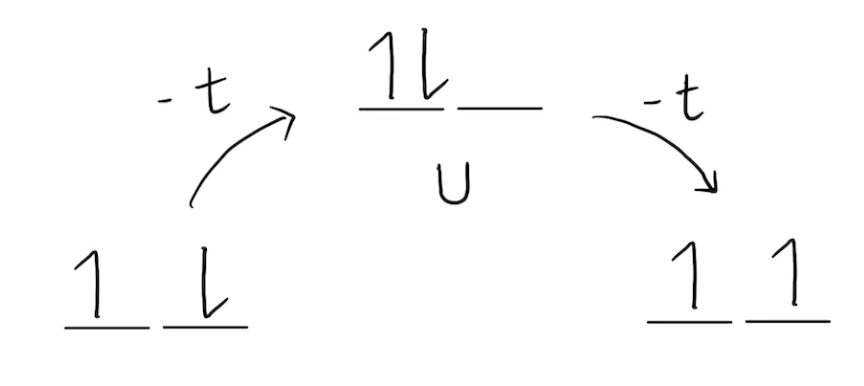
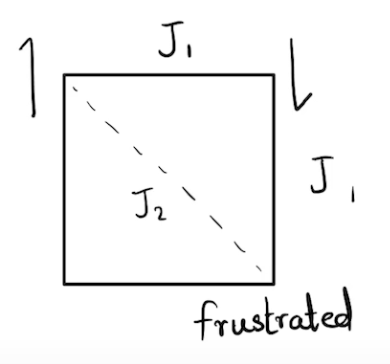
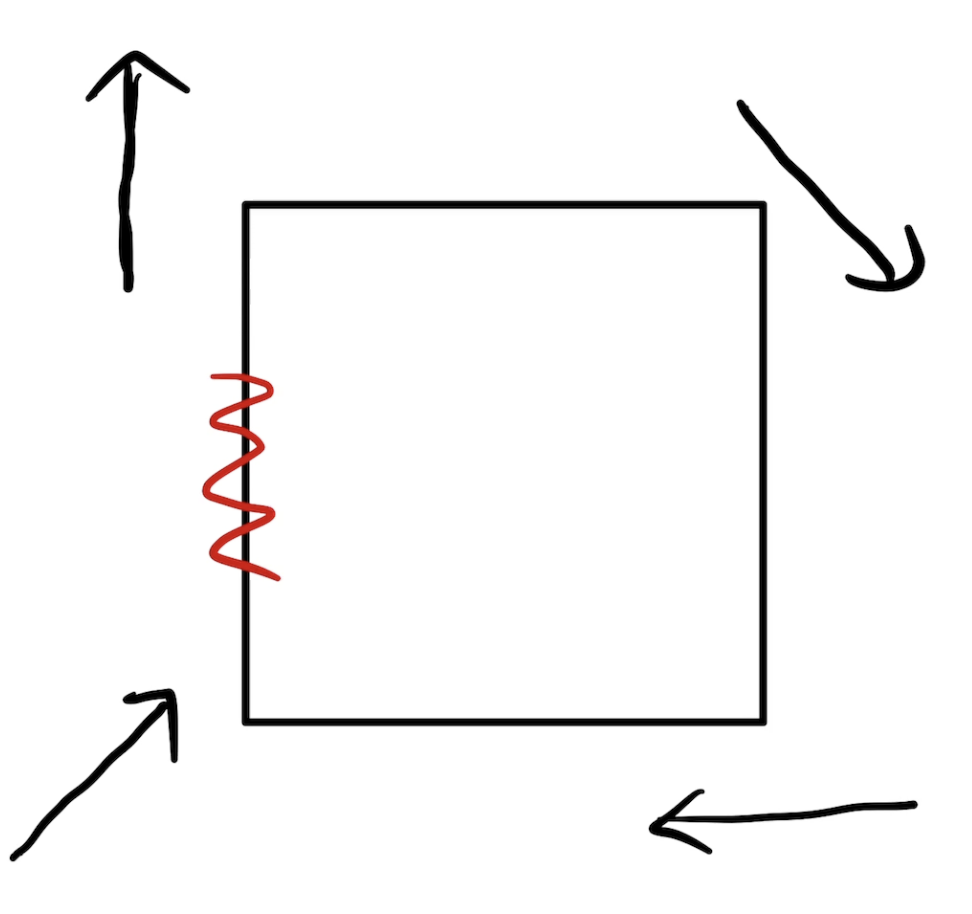
Frustration on a square
with second order interactions?
Two-site spectrum identical to Heisenberg
Partons
\mathbf{S}_i=\dfrac{1}{2}f_{i\alpha}^{\dagger}\mathbf{\sigma}_{\alpha\beta}f_{i\beta}
f_{i\alpha}^{\dagger}f_{i\alpha} = 1
\(f_i\) are spin-1/2 fermions (spinons)
constraint: 1 fermion per site (gauge invariance, \(f_{i\alpha}\rightarrow e^{i\Lambda_i}f_{i\alpha}, A_{ij} \rightarrow A_{ij}+\Lambda_i - \Lambda_j\))
\mathbf{S}_i.\mathbf{S}_j=-\dfrac{1}{2}f_{i\alpha}^{\dagger}f_{j\alpha}f^{\dagger}_{j\beta}f_{i\beta}-\dfrac{1}{4}f_{i\alpha}^{\dagger}f_{i\alpha}f^{\dagger}_{j\beta}f_{j\beta}
Interacting spinons: decouple at mean field level, add gauge field fluctuations
Non-local fractional excitations:
Local excitations have to create spinons in pairs to be gauge invariant: \(f_i^{\dagger}\) is not gauge invariant, \(f_i^{\dagger}f_i\) is
\(f_{1\alpha}^{\dagger}\exp(iA_{12} + iA_{23} +\dots + iA_{(n-1)n})f_{n\alpha}\) is also gauge invariant
Depending on the phase of the gauge field, spinons can be deconfined and are nonlocal
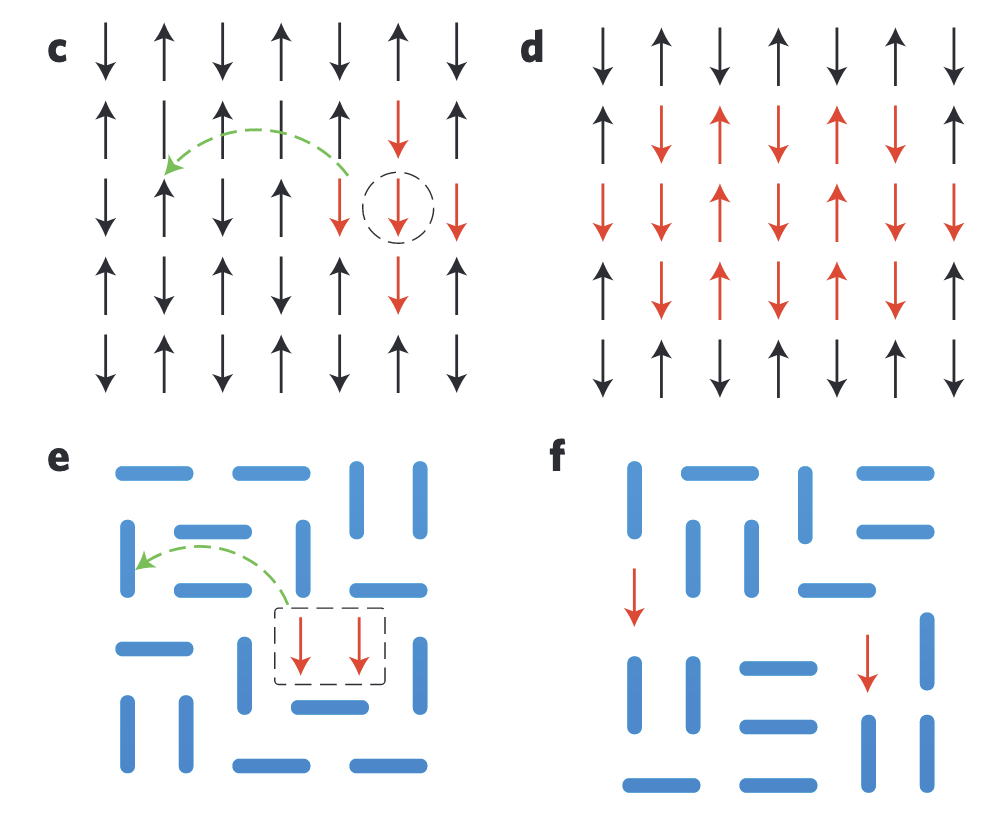
confined in AF
deconfined in QSL
Gutzwiller projection
Instead of gauge fields, project out doublons numerically (with Monte Carlo) from free states
Different noninteracting \(|\Psi_0\rangle\) lead to different QSL
Possible in \(\text{Ba}_4\text{Ir}_3\text{O}_{10}\): \(U(1)\) QSL with \(|\psi_0\rangle\) a metallic free fermion state
spinon
Fermi surface with \(T\)-linear heat capacity
Spin liquid state in
By Ankit Mahajan
