DESI DR2:
BAO Cosmological Constraints
Arnaud de Mattia
CEA Paris-Saclay, Irfu
IPhT, December 17th
Thanks to our sponsors and
72 Participating Institutions!
DESI DR1-5 galaxy samples
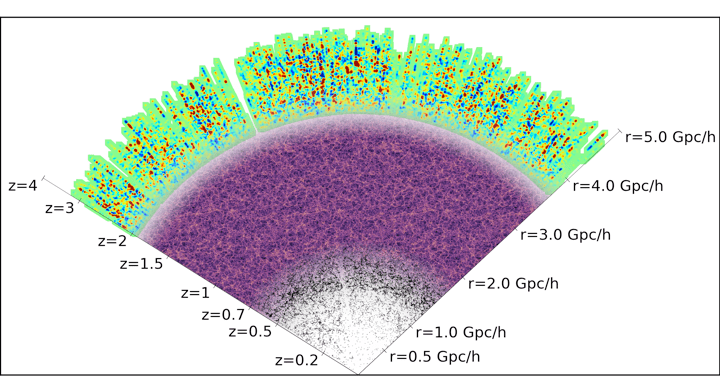
Bright Galaxies: 17M (SDSS: 600k)
0 < z < 0.4
LRG: 14M (SDSS: 1M)
0.4 < z < 1.1
ELG: 30M (SDSS: 200k)
0.6 < z < 1.6
QSO: 3.4M (SDSS: 500k)
Ly\(\alpha\) \(1.8 < z\)
Tracers \(0.8 < z < 2.1\)
8 years \(\sim 63\)M galaxy redshifts over 17k \(\mathrm{deg}^2\)
\(z = 0.4\)
\(z = 0.8\)
\(z = 0\)
\(z = 1.6\)
\(z = 2.0\)
\(z = 3.0\)
DESI data release 2 (DR2)
Observations from May 14th 2021 to April 9th 2024
approved
construction started
first light
survey started
DR1 data sample
DR1 results
DR2 sample secured
DR3
DR2 results
2015
16
17
18
19
20
22
23
24
21
25
26
27
DESI data release 2 (DR2)
- 30M galaxy and QSO redshifts in 3 years of operation
- 14M used in the DR2 analysis (6M in DR1)
- Including 820,000 Ly\(\alpha\) QSO at \(z > 2.09\) (420,000 in DR1)
- \(> 2\times\) increase in number of tracers
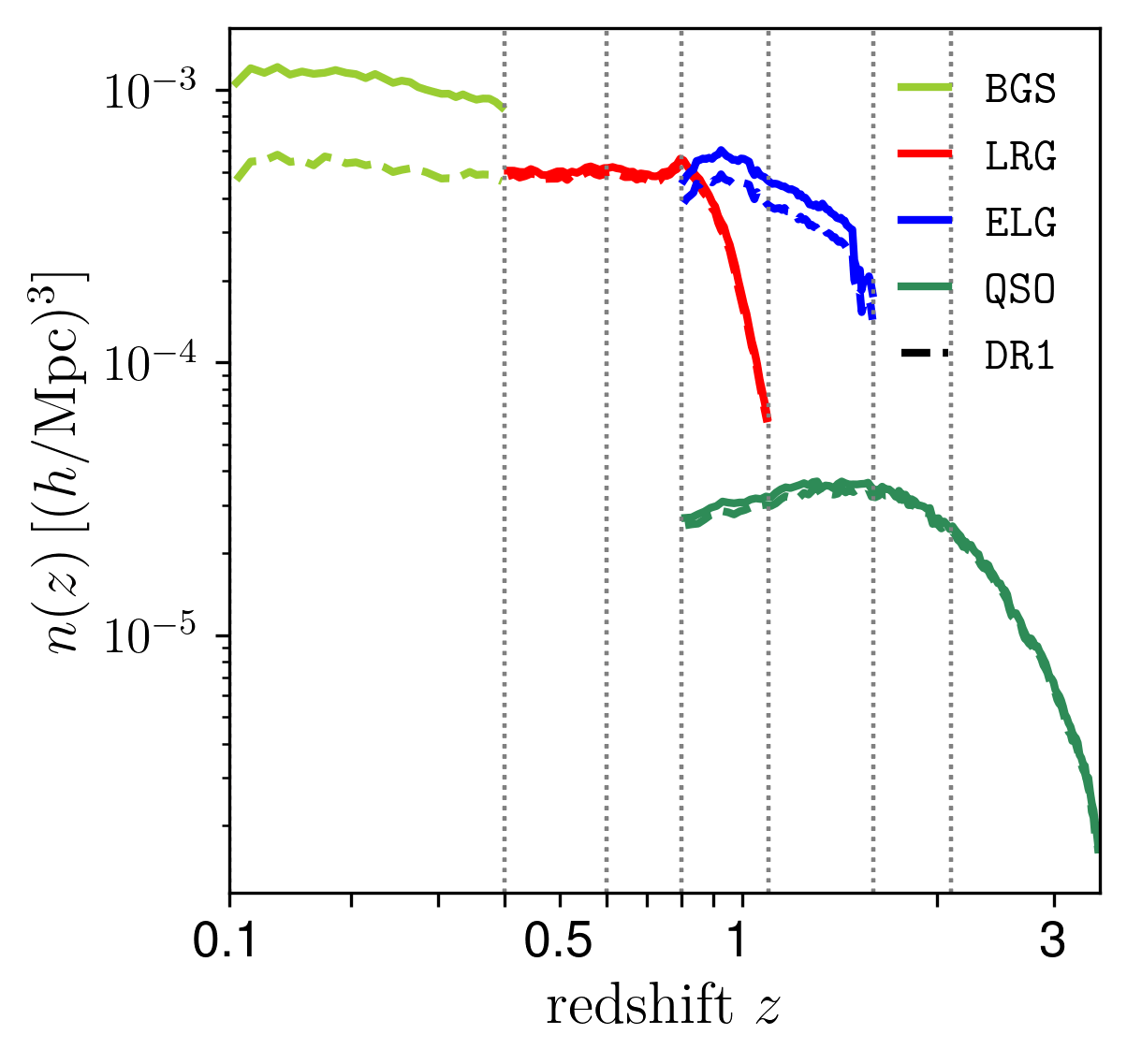
higher completeness (deeper)
extended mag cut
Release of DESI DR2 (BAO) results
March 19th 2025
First batch of DESI DR2 cosmological analyses: https://data.desi.lbl.gov/doc/papers/dr2
• DESI Collaboration et al. (2025), DESI DR2 Results I: Baryon Acoustic Oscillations from the Lyman Alpha Forest
• DESI Collaboration et al. (2025), DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints
Companion supporting papers:
Lodha et al. (2025), Extended Dark Energy analysis
Elbers et al. (2025), Constraints on Neutrino Physics
Andrade et al. (2025), Validation of the DESI DR2 BAO mesurements
Casas et al. (2025), Validation of the DESI DR2 Lyα BAO analysis using synthetic datasets
Brodzeller et al. (2025), Construction of the Damped Lyα Absorber Catalog for DESI DR2 Lyα BAO
DR1 public!
BAO measurements
- angle on the sky (transverse to the line-of-sight): \(\theta_\mathrm{BAO} = \orange{r_\mathrm{d}}/\green{D_\mathrm{M}(z)}\)
- \(\Delta z\) (along the line-of-sight): \( \Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z) = \green{H(z)} \orange{r_\mathrm{d}} / c \)
- at multiple redshifts \(z\)
Probes the expansion history (\(\green{D_\mathrm{M}, D_H}\)), hence the energy content (e.g. dark energy)
Absolute size at \(z = 0\): \(H_0 \orange{r_\mathrm{d}}\)
z_1
z_2
z_3
BAO measurements
correlation function
BAO peak
line of sight
monopole
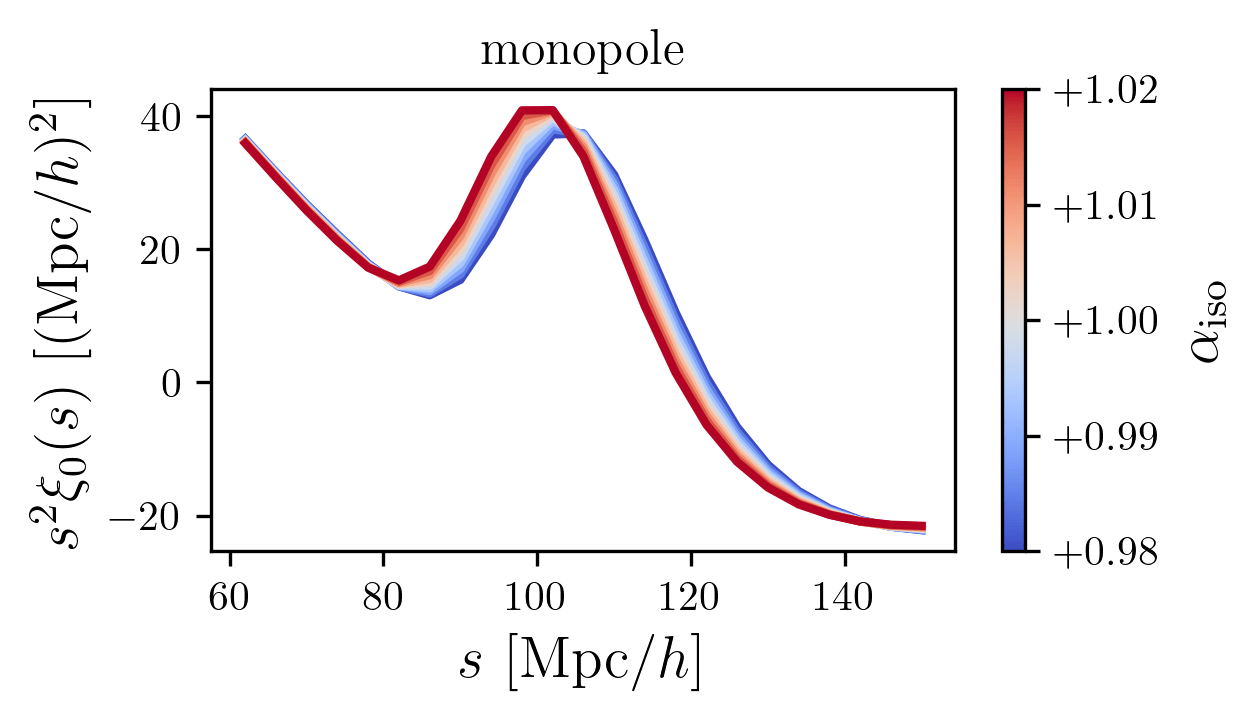
BAO measurements
correlation function
\alpha_\mathrm{iso} \propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
BAO peak
line of sight
monopole
isotropic
comoving transverse distance
Hubble distance \(c/H(z)\)
sound horizon (standard ruler)
BAO measurements
isotropic
anisotropic
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)
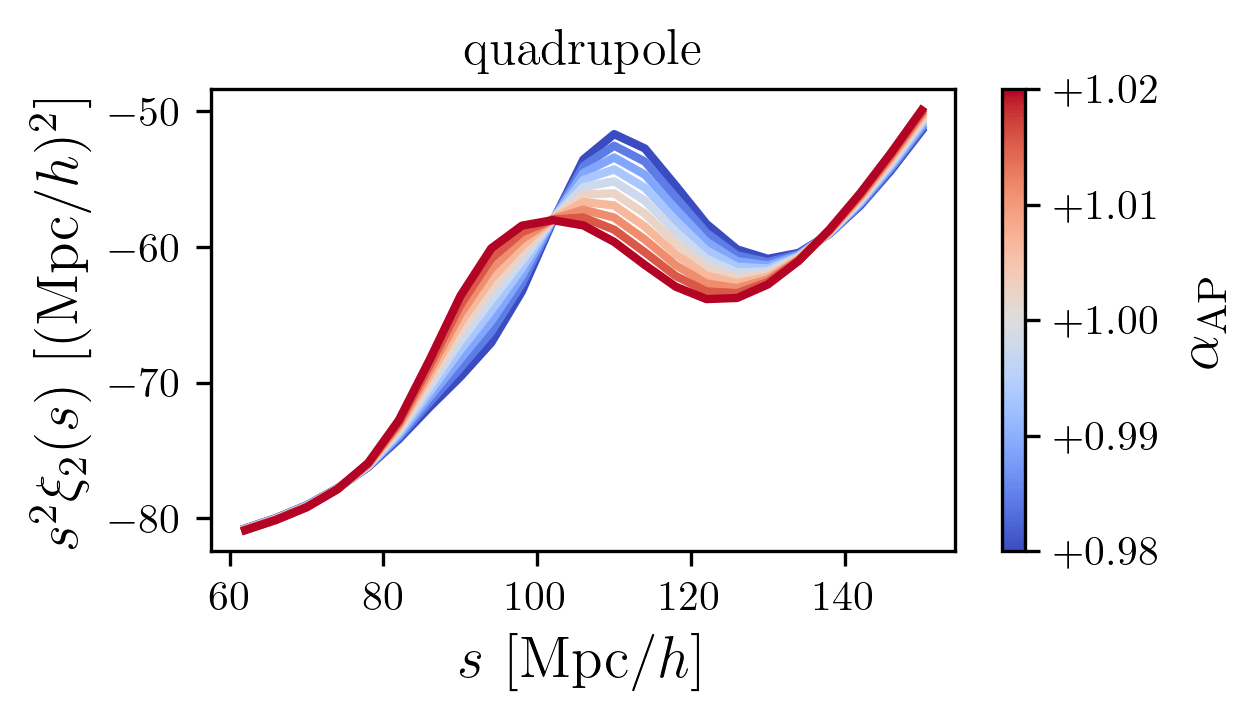
BAO peak
line of sight
line of sight
monopole
quadrupole
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
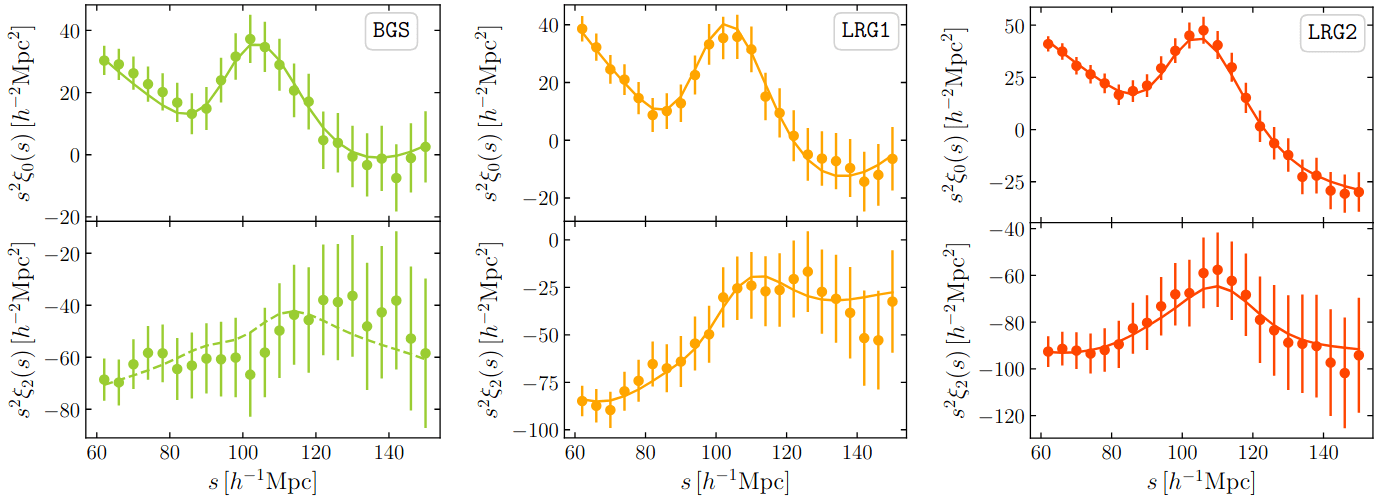
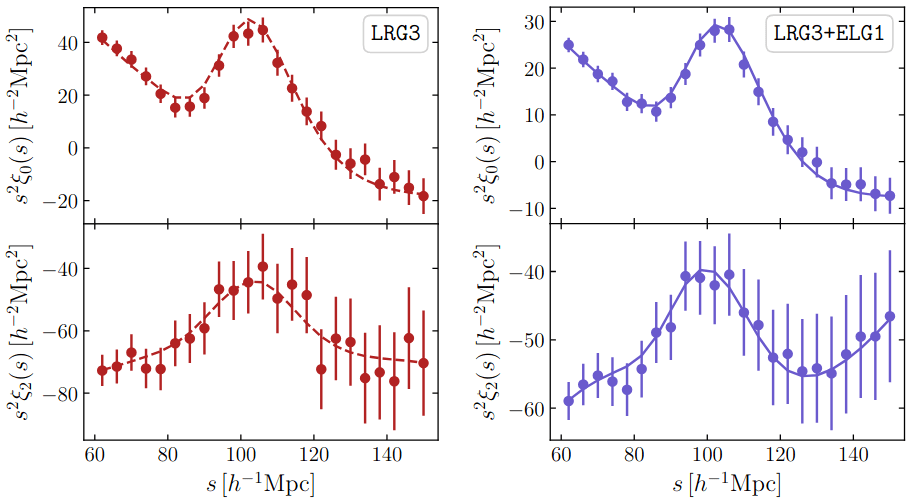
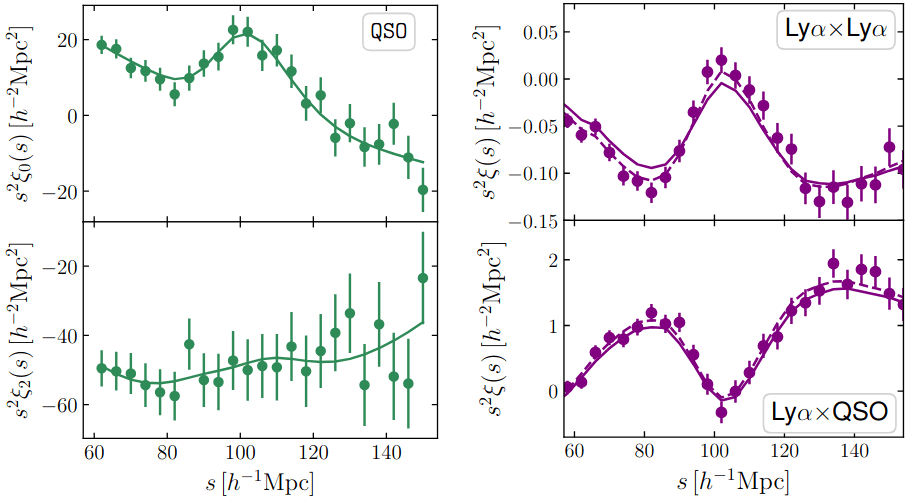
low S/N
BAO detection: \(14.7\sigma\)
0.1 < z < 0.4
0.4 < z < 0.6
0.6 < z < 0.8
0.8 < z < 1.1
1.1 < z < 1.6
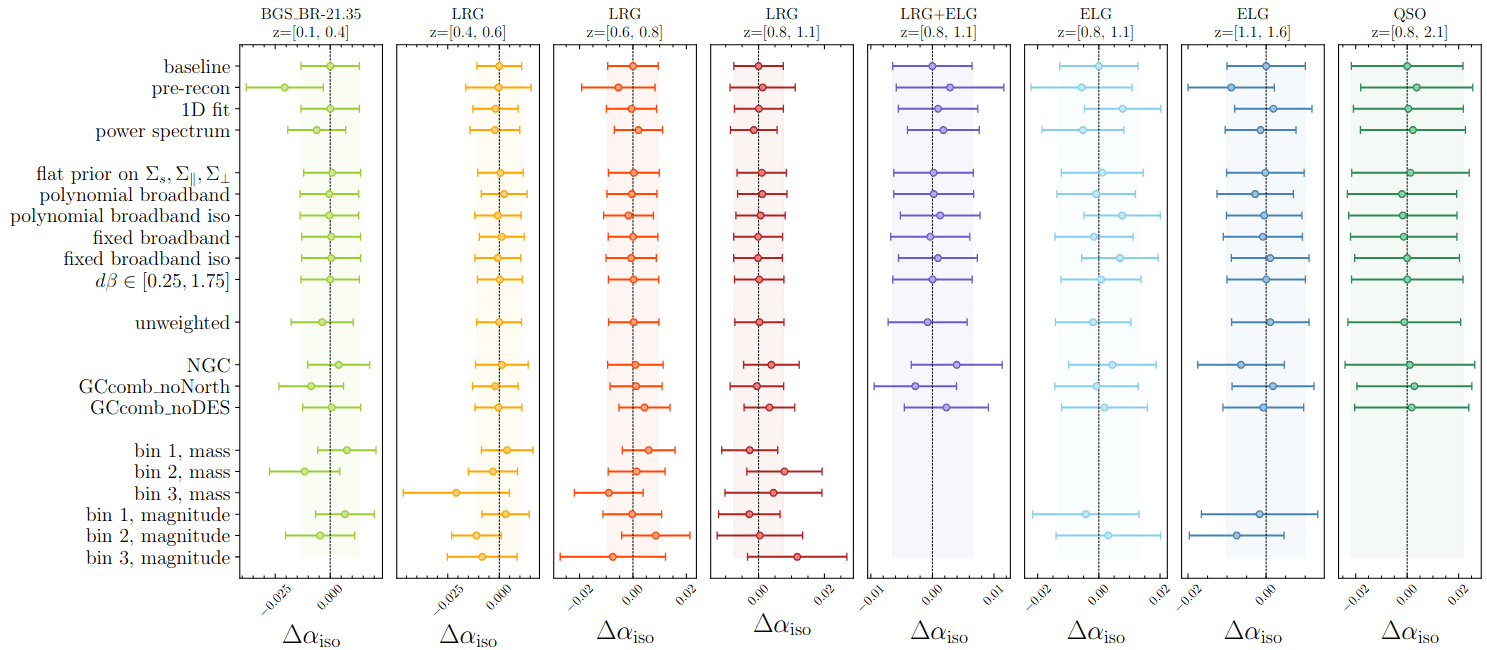
Robustness tests
tracers / redshift bins
data vector
Robustness tests
tracers / redshift bins
BAO modelling
Robustness tests
tracers / redshift bins
imaging systematics
Robustness tests
tracers / redshift bins
data splits
Ly\(\alpha\) forest
Ly\(\alpha\) forest
Absorption in QSO spectra by neutral hydrogen in the intergalactic medium: \(\lambda_\mathrm{abs} = (1 + z_\mathrm{HI}) \times 1215.17 \; \AA \)
Transmitted flux fraction \(F = e^{-\tau}\) probes the fluctuation in neutral hydrogen density, \(\tau \propto n_\mathrm{HI} \)
credit: Andrew Pontzen
Correlation functions
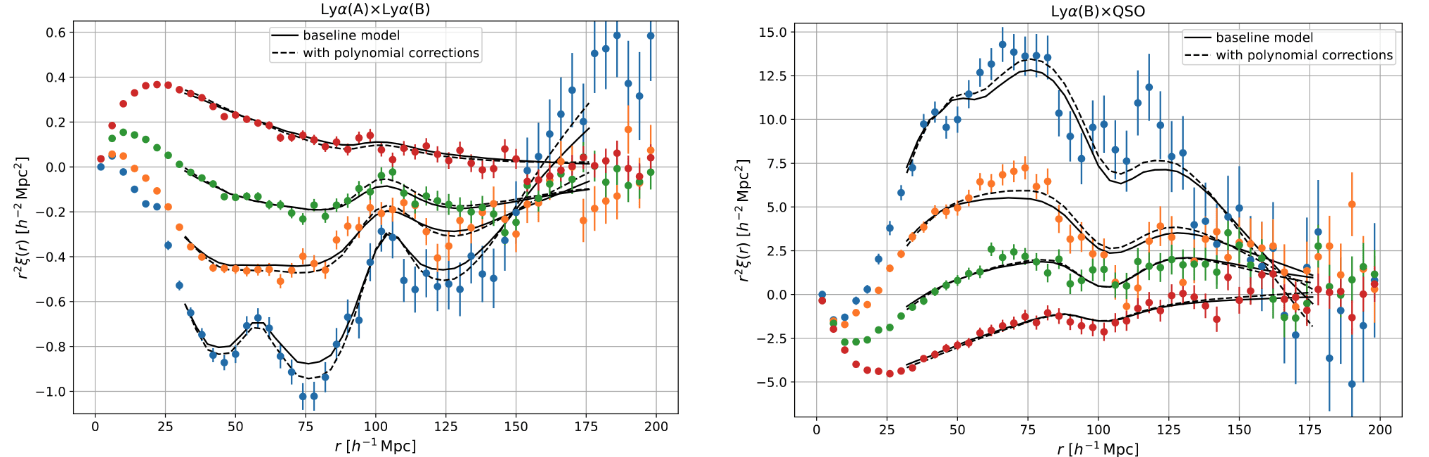
Ly\(\alpha\) forest auto-correlation
\(\langle \delta_F(\mathbf{x}) \delta_F(\mathbf{x + s}) \rangle\)
Ly\(\alpha\) forest - QSO cross-correlation
\(\langle \delta_F(\mathbf{x}) Q(\mathbf{x + s}) \rangle\)
Robustness tests
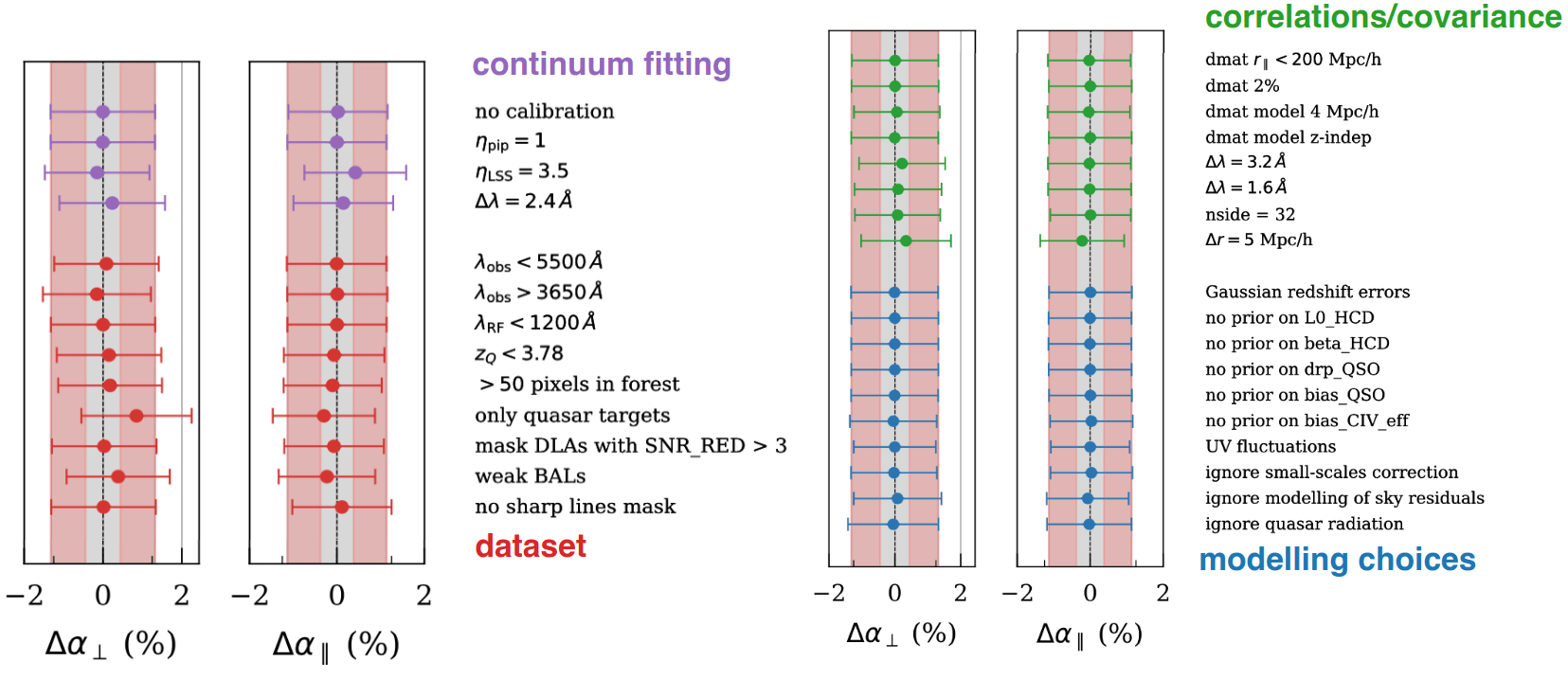
data vector / covariance
Robustness tests
modelling choices
Robustness tests
continuum fitting
Robustness tests
data splits
DESI DR2 BAO
DESI DR2 BAO measurements
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
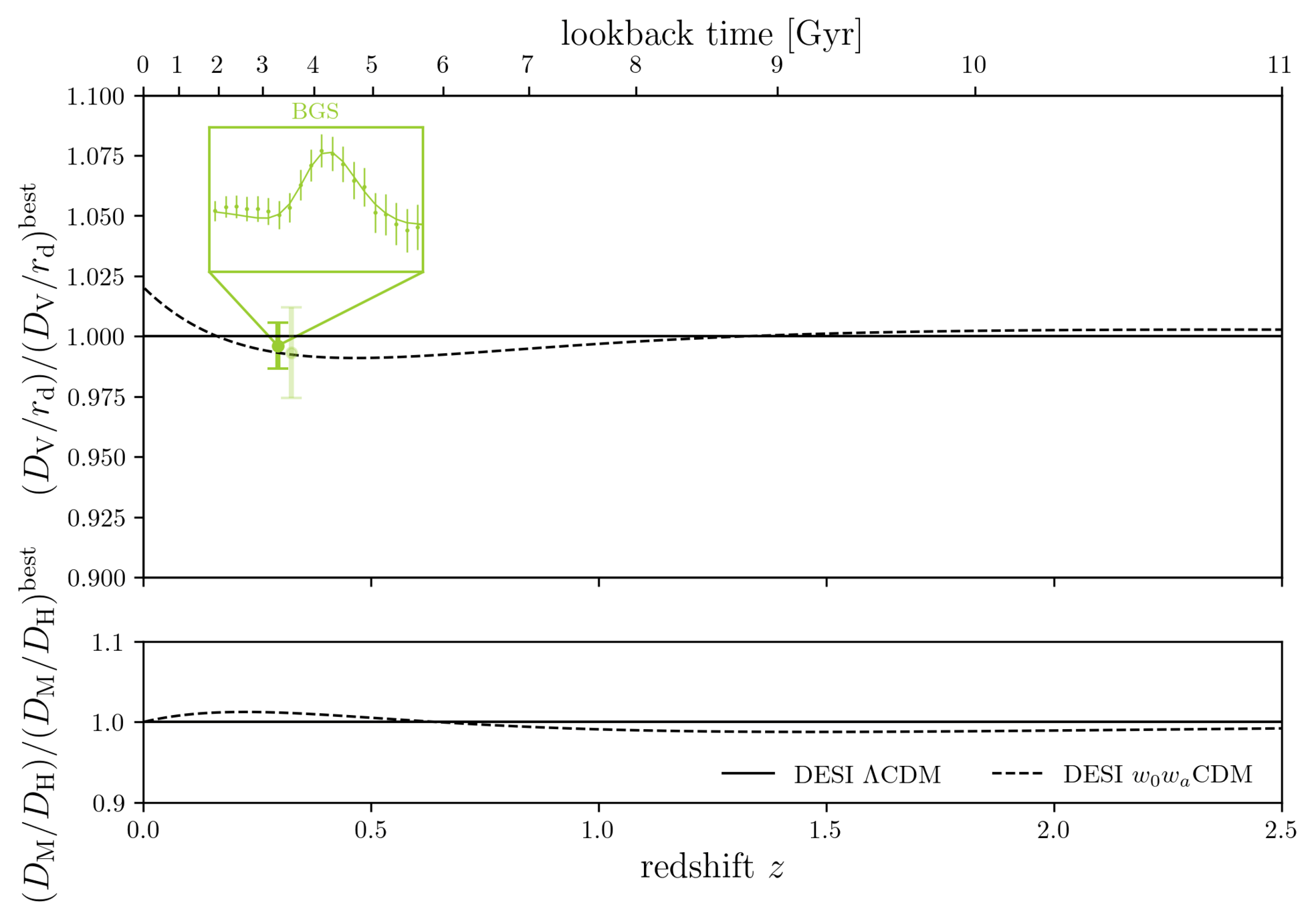
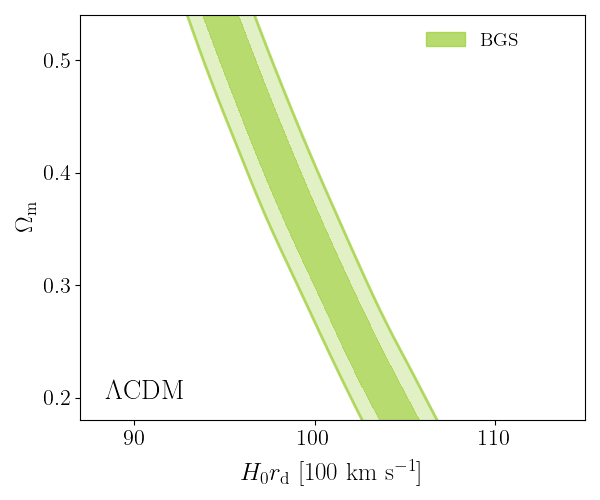
DESI DR2 BAO
DESI DR2 BAO measurements
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z) = f(\Omega_\mathrm{m})
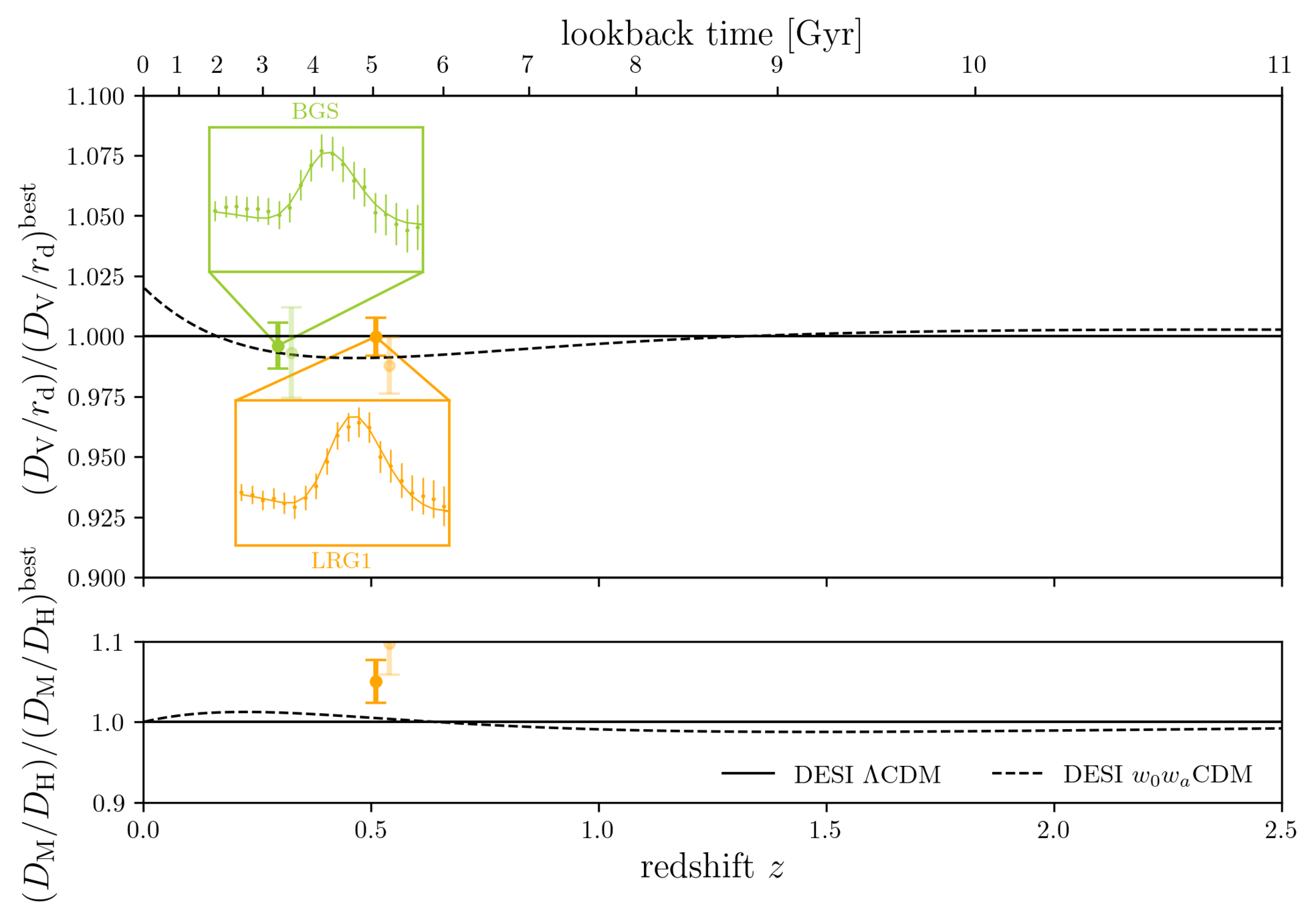
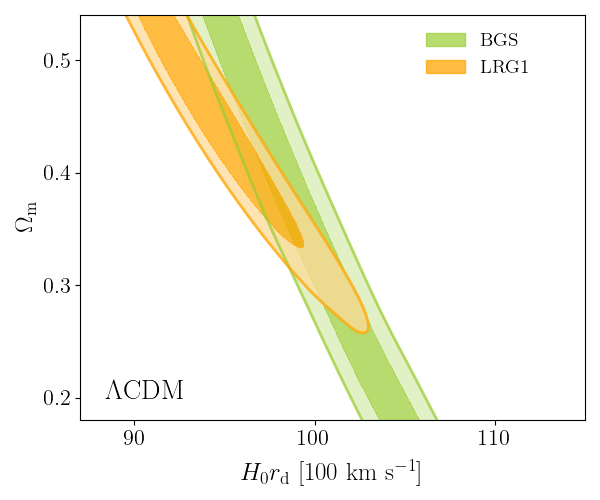
DESI DR2 BAO
DESI DR2 BAO measurements
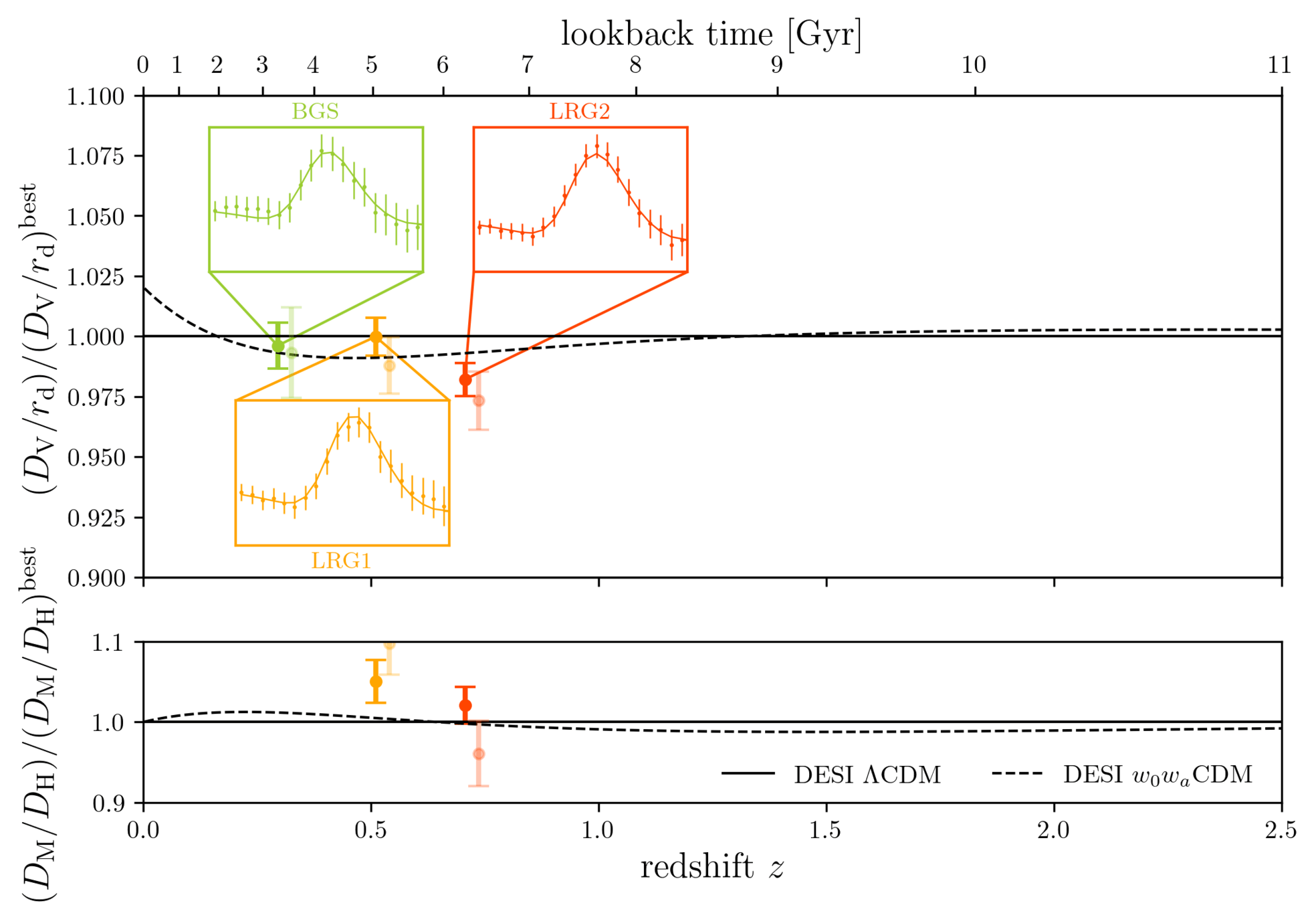
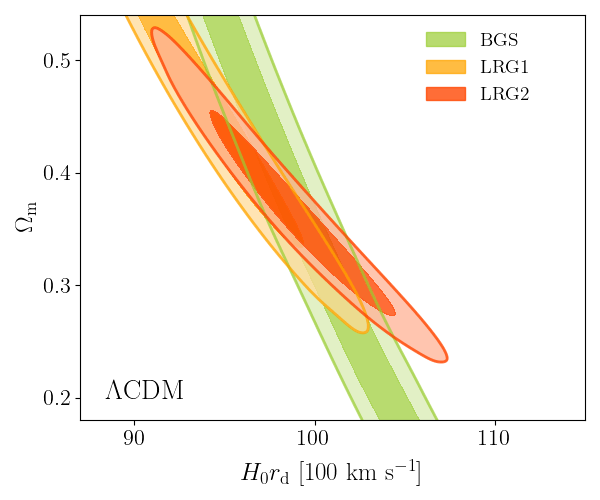
DESI DR2 BAO
DESI DR2 BAO measurements
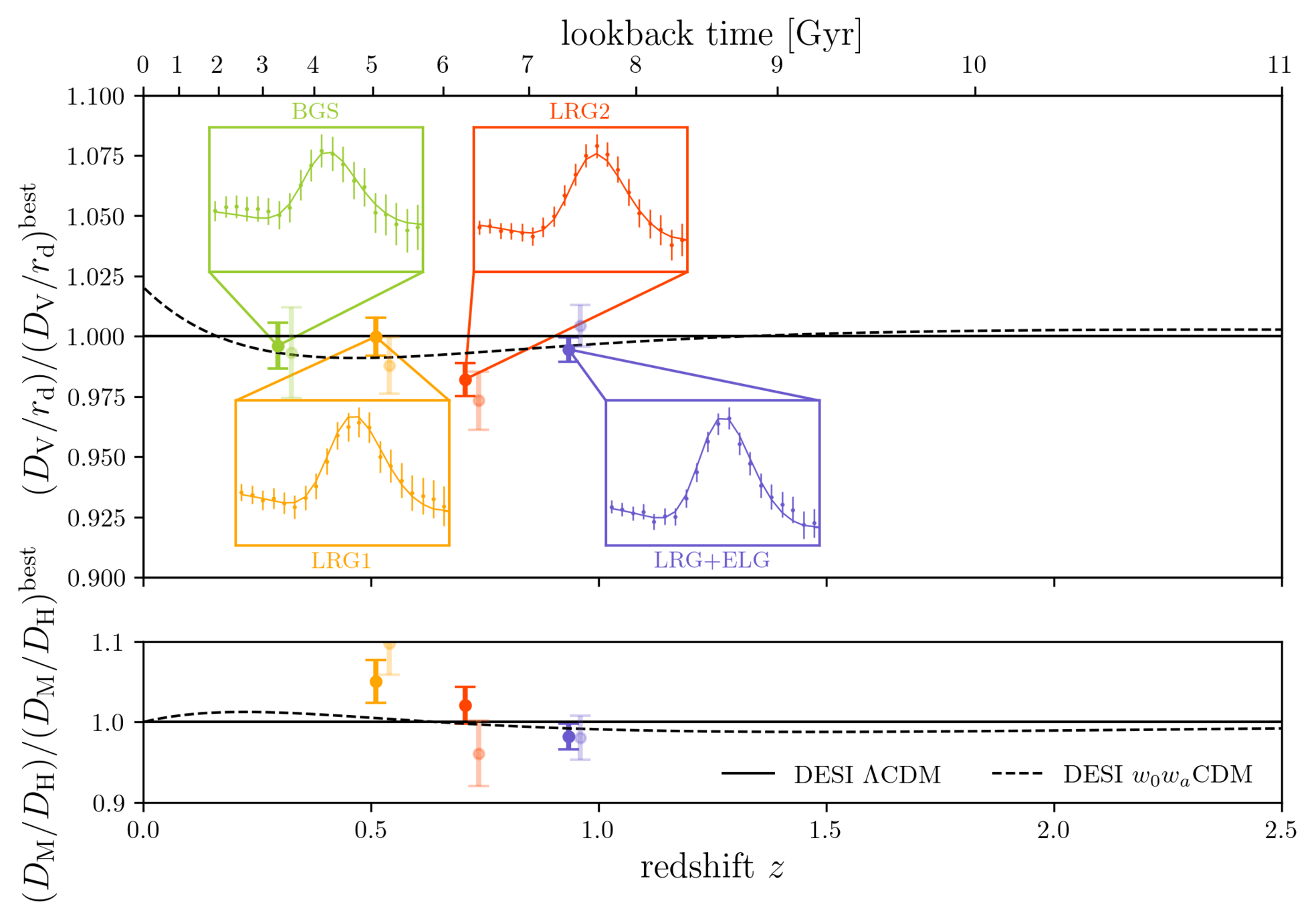
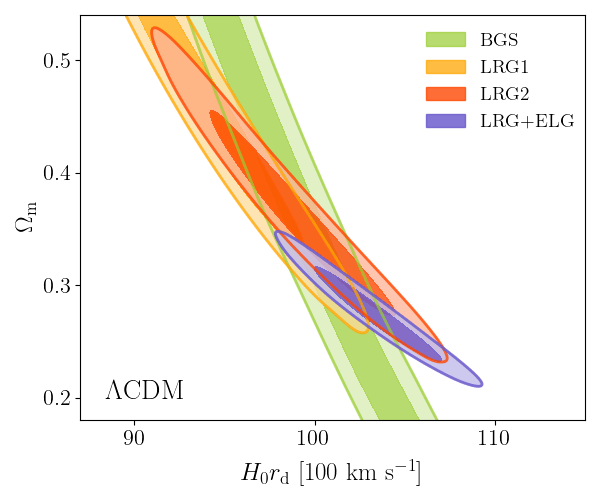
DESI DR2 BAO
DESI DR2 BAO measurements
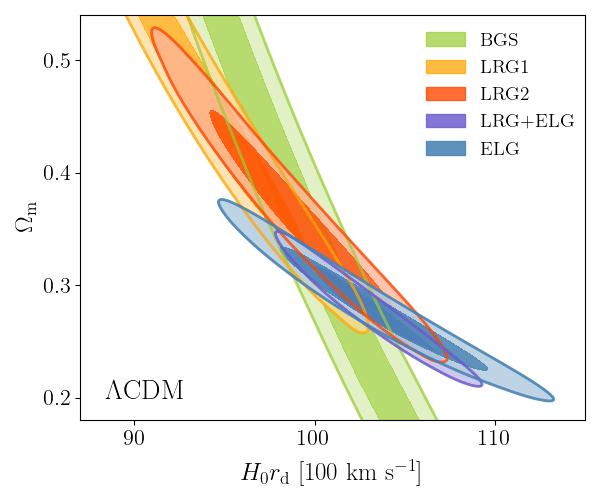
DESI DR2 BAO
DESI DR2 BAO measurements
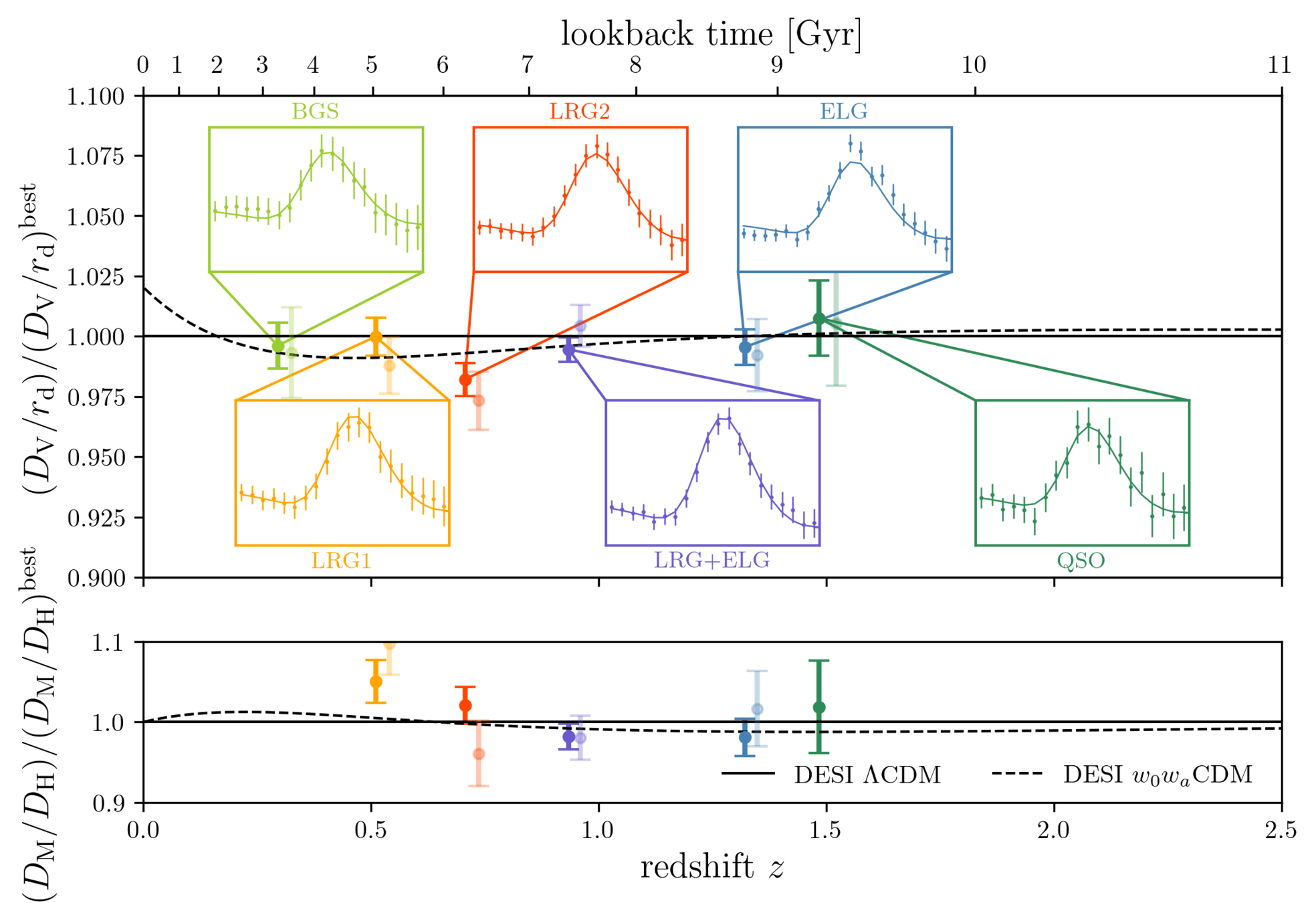
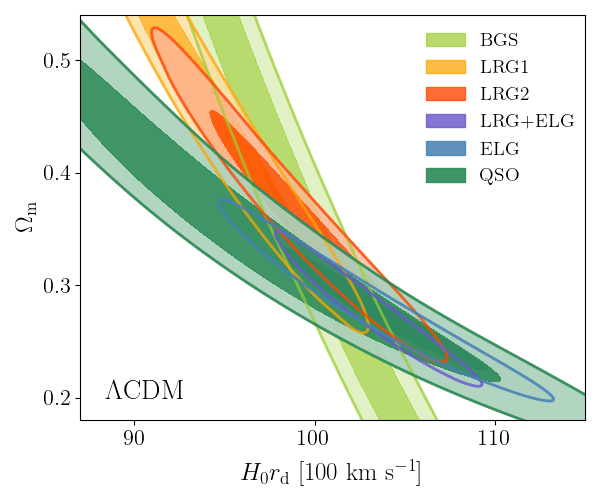
DESI DR2 BAO
DESI DR2 BAO measurements
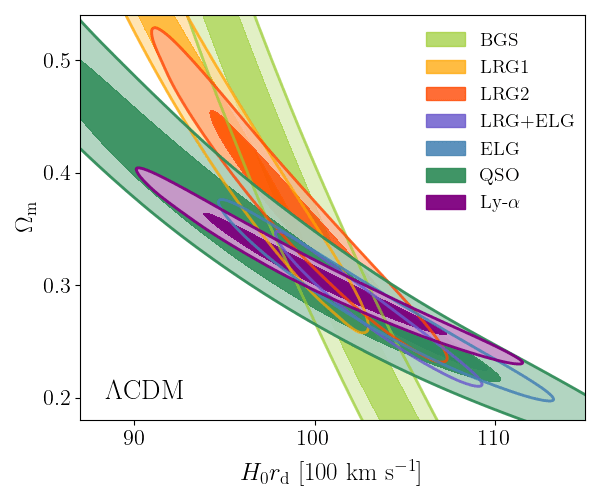
Consistent with each other,
and complementary
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.2975 \pm 0.0086 & \mathbf{(3.0\%)} \\
H_{0} r_\mathrm{d} &= (101.54 \pm 0.73) \, [100 \, \mathrm{km} \, \mathrm{s}^{-1}] & \mathbf{(0.7\%)}
\end{align*}}_{\textstyle \text{\color{black}{DESI}}}
DESI DR2 BAO
DESI DR2 BAO measurements
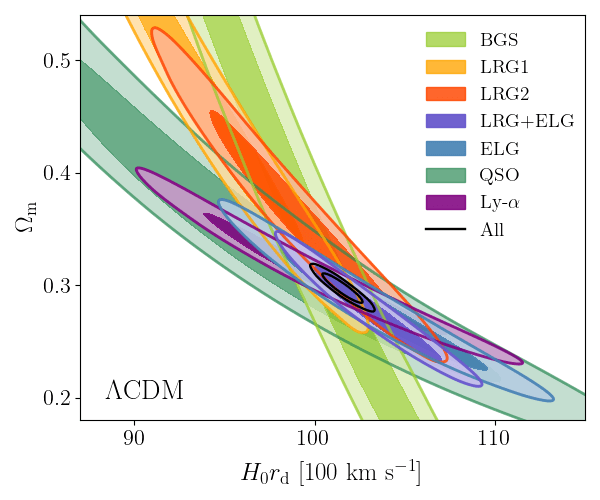
- DESI DR2 BAO fully consistent with DESI DR1
- Improvement of \(\simeq 40\%\)
- \(2.3 \sigma\) discrepancy with primary CMB¹ + CMB lensing²
BAO vs CMB
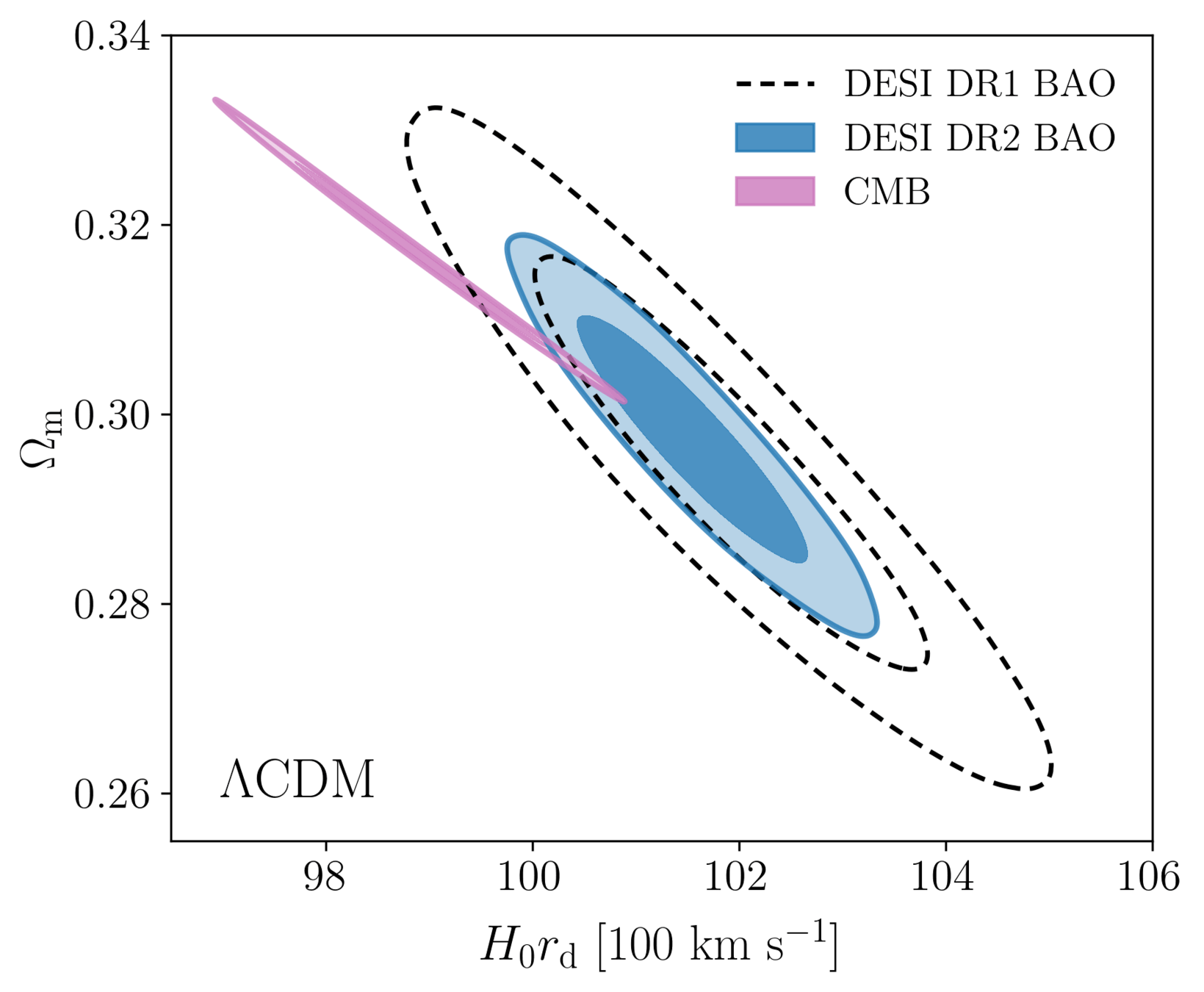
1. Planck PR4 CamSpec
2. Planck PR4 + ACT DR6 lensing
DESI DR2 / DR1 vs Planck
\(\mathcal{D}_\parallel, \mathcal{D}_\perp = \mathrm{Rot}(D_\mathrm{H}/r_\mathrm{d}, D_\mathrm{M}/r_\mathrm{d})\) with \(\mathcal{D}_\perp\) best constrained by Planck
following Efstathiou+25
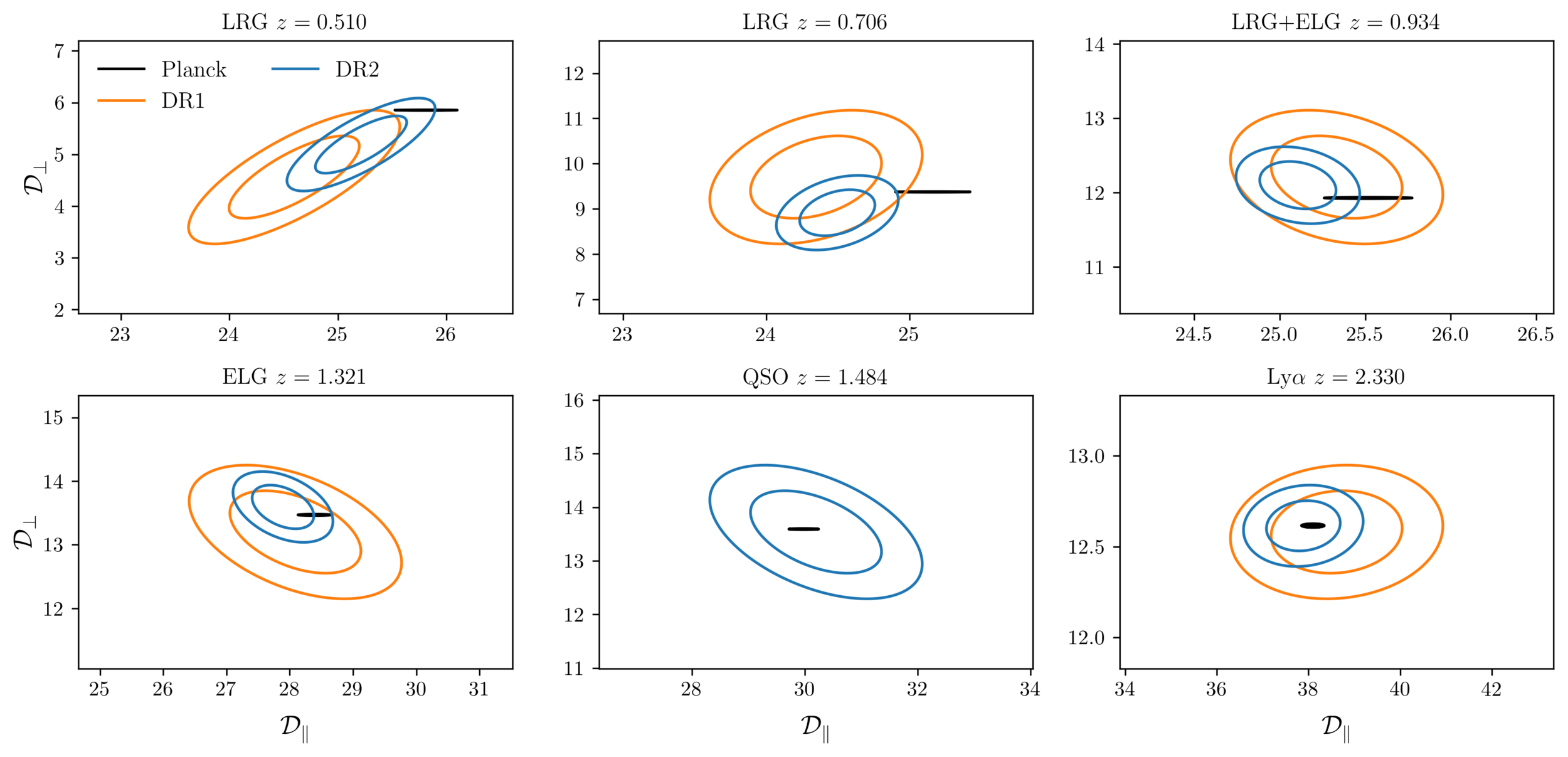
DESI DR2 / DR1 vs Planck
following Efstathiou+25
turned into \(\omega_\mathrm{bc}\) constraint
DR2 more consistent
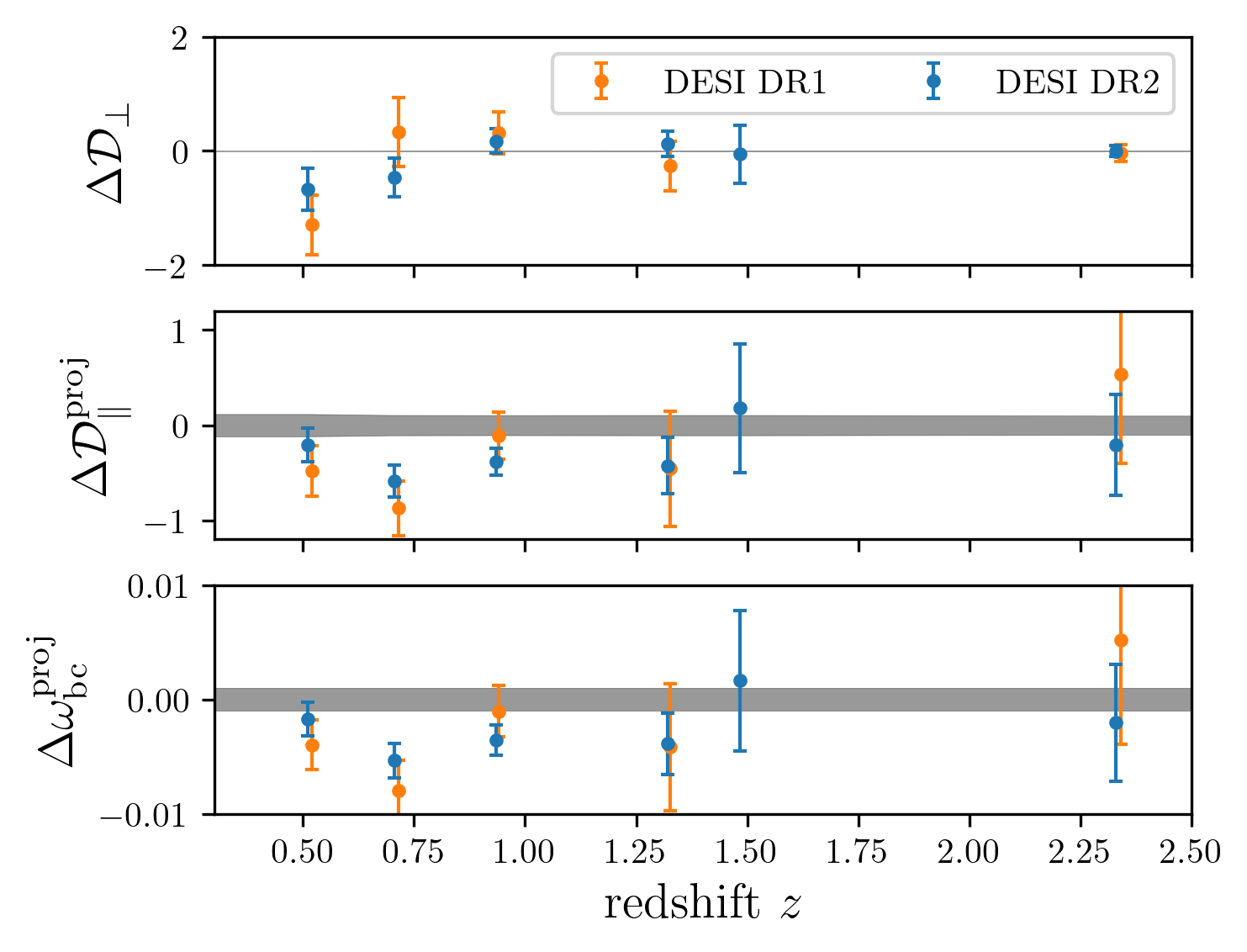
DESI DR2 / DR1 vs Planck
\(\omega_\mathrm{bc}\)
- \(2.3 \sigma\) discrepancy with primary CMB + CMB lensing
DESI DR2 / DR1 vs Planck
following Efstathiou+25
With CMB = low-\(\ell\) PR3 + CamSpec PR4 + (ACT+PR4) lensing
\(H_0r_\mathrm{d}, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(2.3\sigma\)
\(2.2\sigma\)
\(2.2\sigma\)
\(1.8\sigma\)
\(1.9\sigma\)
\(2.1\sigma\)
\(0.8\sigma\)
\(2.6\sigma\)
\(2.7\sigma\)
\(1.3\sigma\)
\(2.1\sigma\)
\(2.3\sigma\)
no isotropic BAO
multiple counting of Planck uncertainty
where there is most discrepancy
DESI DR2 / DR1 vs Planck
following Efstathiou+25
With CMB = low-\(\ell\) PR3 + CamSpec PR4
\(H_0r_\mathrm{d}, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(2.3\sigma\) \(1.9\sigma\)
\(2.2\sigma\) \(1.9\sigma\)
\(2.2\sigma\) \(1.9\sigma\)
\(1.8\sigma\) \(1.6\sigma\)
\(1.9\sigma\) \(1.7\sigma\)
\(2.1\sigma\) \(2.0\sigma\)
\(0.8\sigma\)
\(2.6\sigma\) \(2.2\sigma\)
\(2.7\sigma\) \(2.3\sigma\)
\(1.3\sigma\)
\(2.1\sigma\) \(1.9\sigma\)
\(2.3\sigma\) \(2.1\sigma\)
no isotropic BAO
multiple counting of Planck uncertainty
where there is most discrepancy
BAO vs CMB
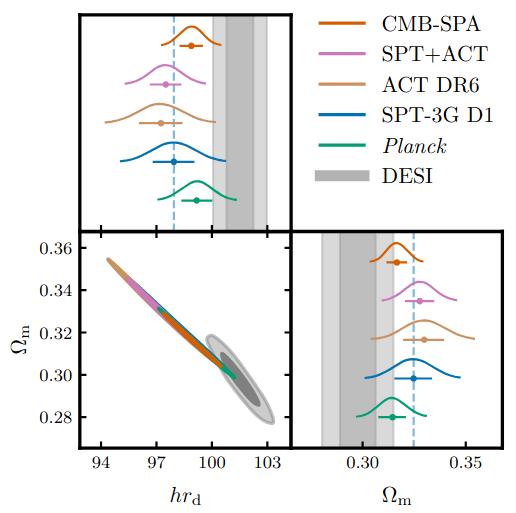
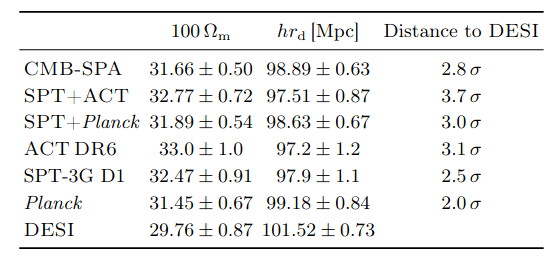
SPA = SPT+Planck+ACT
Curvature \(\Omega_\mathrm{k}\)
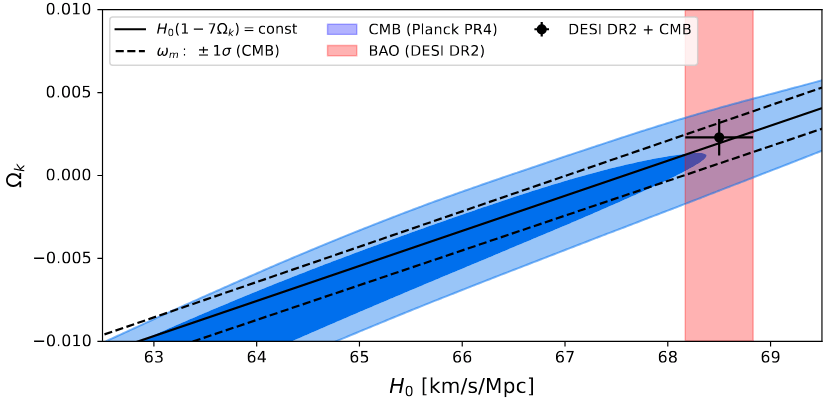
CMB \(\theta_\star\) constrains \(\Omega_\mathrm{m}h^3(1-7\Omega_\mathrm{k})\)
\(\Omega_\mathrm{k} = 0.0023 \pm 0.0011\) (DESI + CMB)
\(\Lambda\mathrm{CDM}\) constraints
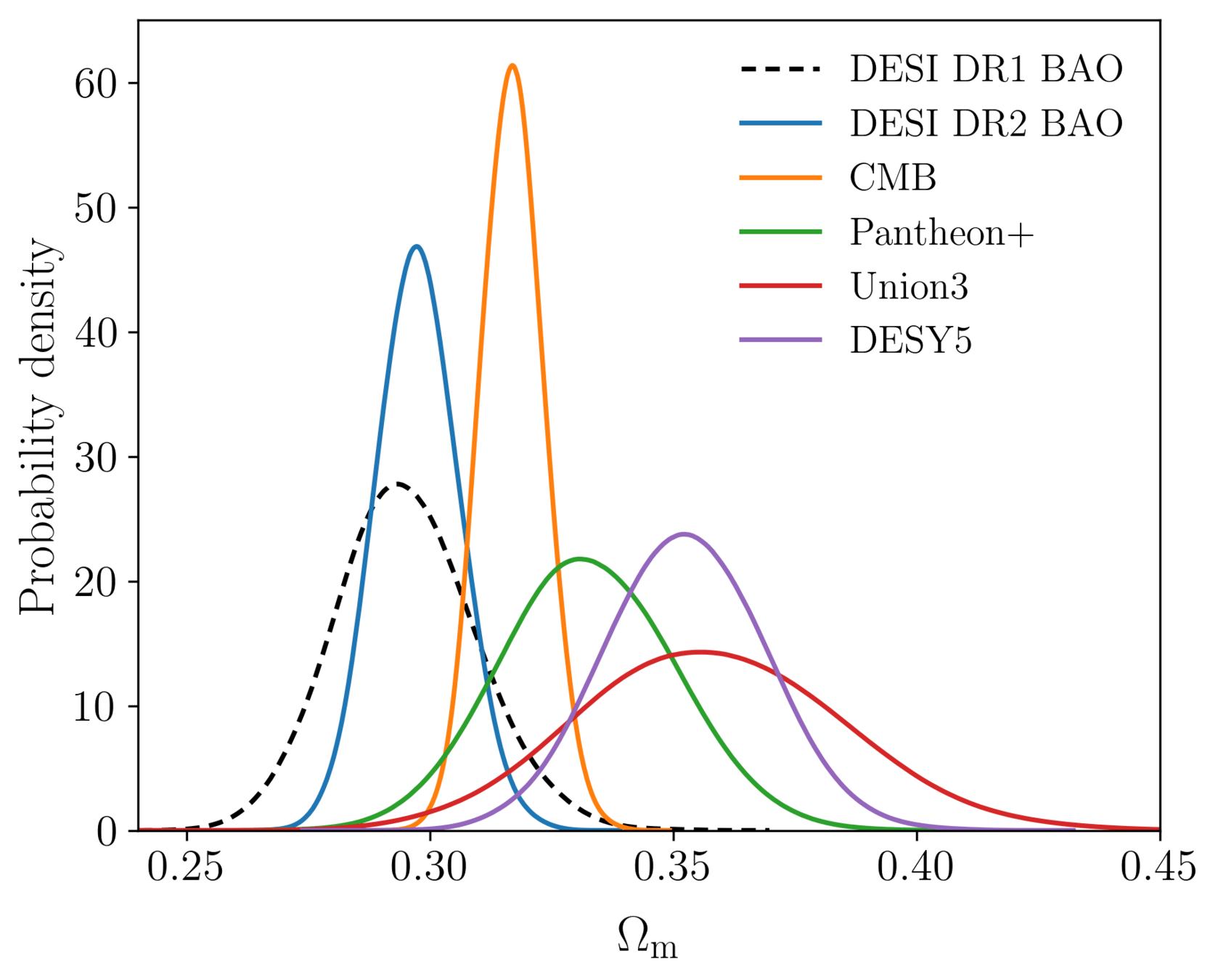
- DESI \(\Omega_\mathrm{m}\) lower than the CMB (\(1.8\sigma\))
-
DESI \(\Omega_\mathrm{m}\) lower than SN:
- Pantheon+: \(1.7\sigma\)
- Union3: \(2.1\sigma\)
- DESY5: \(2.9\sigma\)
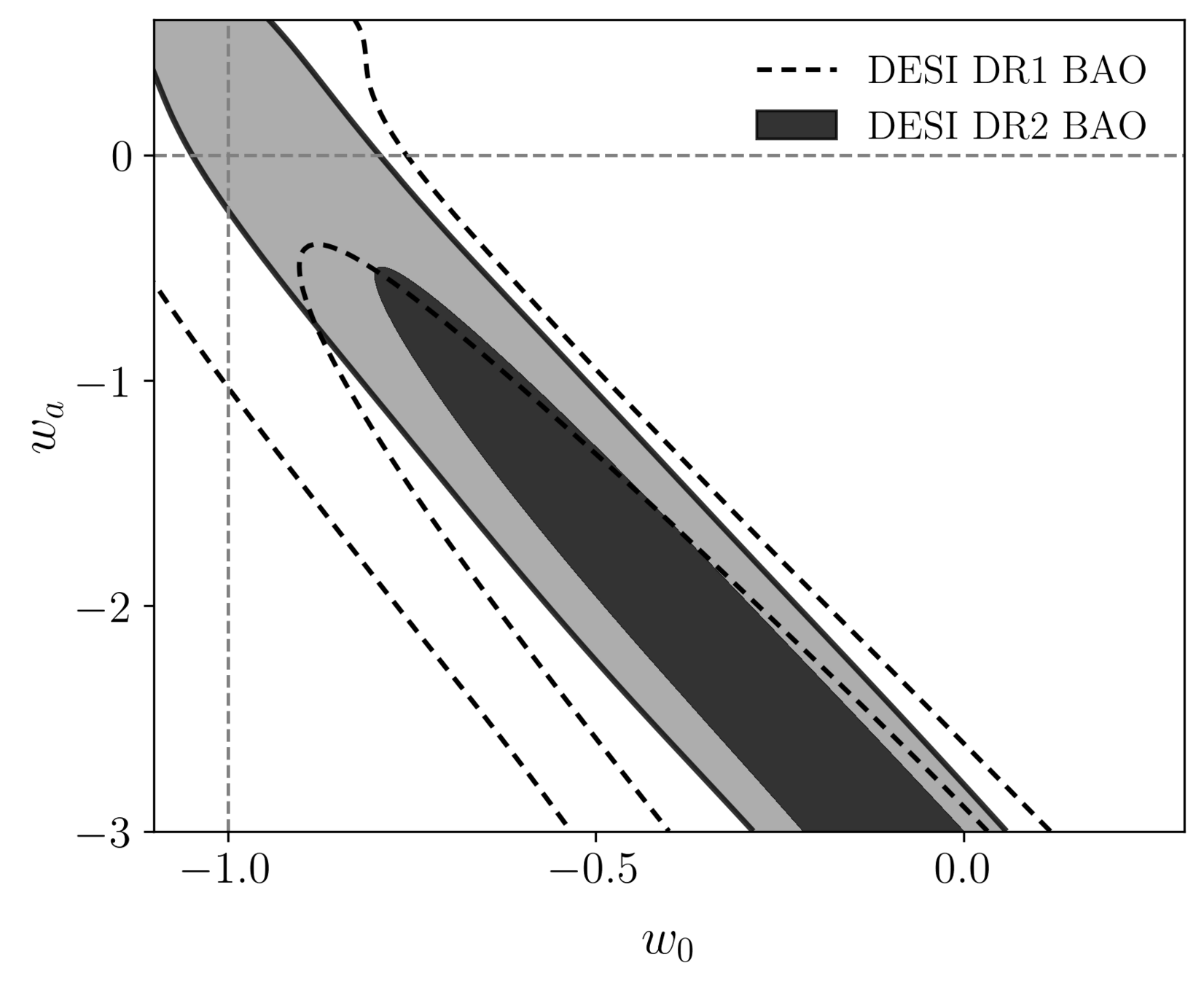
- Dark energy fluid
- No strong preference for dark energy evolution: \(1.7\sigma\) from DESI data alone
Dark Energy Equation of State
\(\Lambda\)
p / \rho = w = w_0 + w_a (1 - a)
pressure
density
CPL
- Combining DESI + CMB:
Dark Energy Equation of State
\underbrace{
w_{0} = -0.42 \pm 0.21 \qquad w_{a} = -1.75 \pm 0.58
}_{\textstyle \textcolor{orange}{\text{DESI + CMB} \; \implies \; 3.1\sigma}}
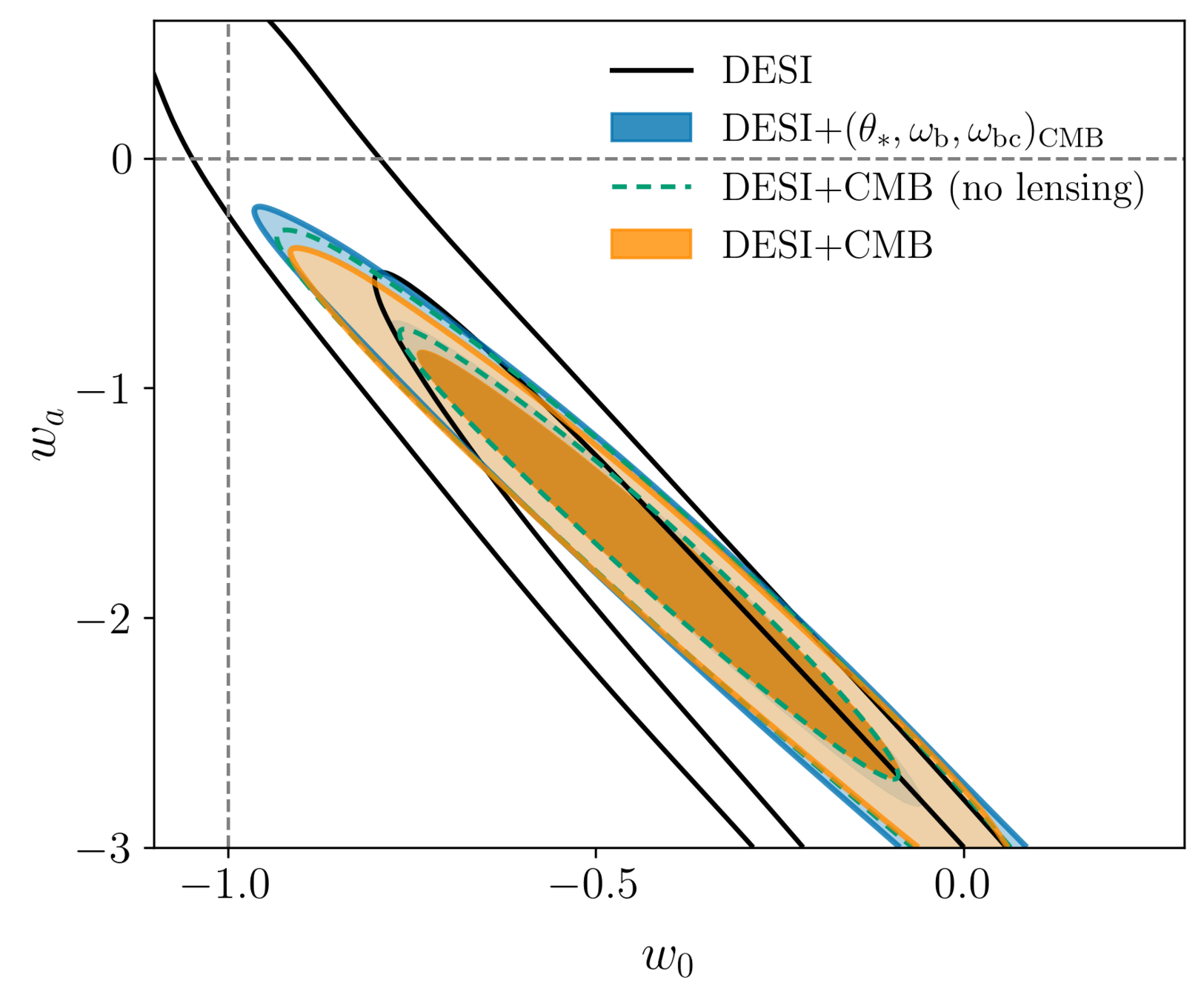
- CMB early-Universe priors: \(2.4\sigma\)
- Without CMB lensing \(2.7\sigma\)
\(+0.5\sigma\) compared to DR1
Dark Energy Equation of State
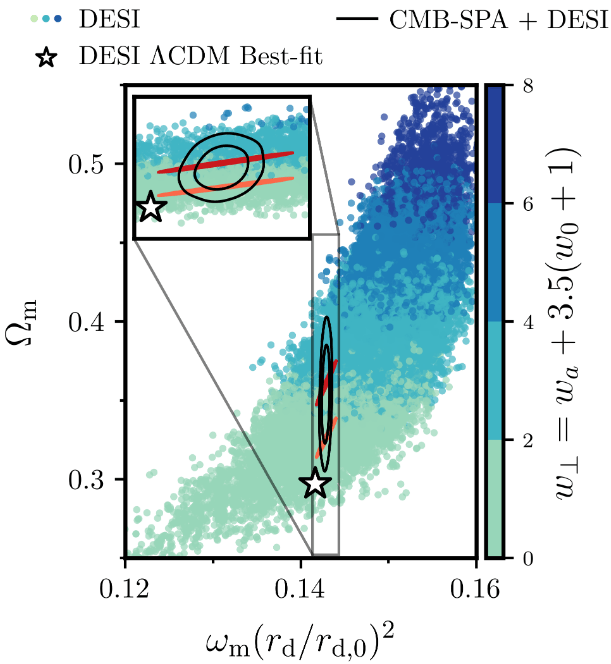
constrained by CMB
Dark Energy EoS (with SN)
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.838 \pm 0.055 \qquad w_{a} = -0.62^{+0.22}_{-0.19}
}_{\textstyle \textcolor{blue}{\text{DESI + CMB + Pantheon+} \; \implies \; 2.8\sigma}}
\underbrace{
w_{0} = -0.667 \pm 0.088 \qquad w_{a} = -1.09^{+0.31}_{-0.27}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.8\sigma}}
\underbrace{
w_{0} = -0.752 \pm 0.057 \qquad w_{a} = -0.86^{+0.23}_{-0.20}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 4.2\sigma}}
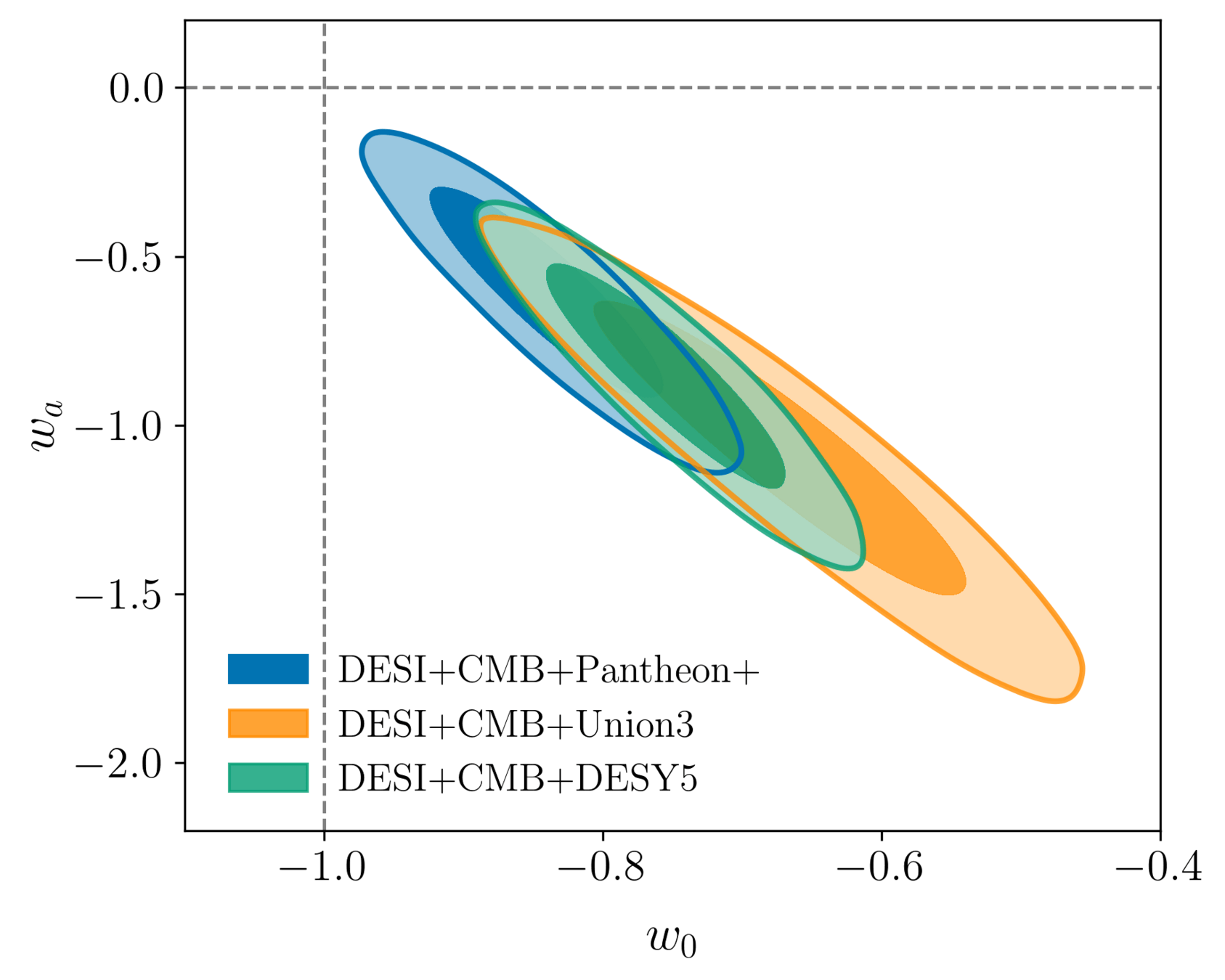
\(+0.3\sigma\) compared to DR1
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.838 \pm 0.055 \qquad w_{a} = -0.62^{+0.22}_{-0.19}
}_{\textstyle \textcolor{blue}{\text{DESI + CMB + Pantheon+} \; \implies \; 2.8\sigma}}
\underbrace{
w_{0} = -0.667 \pm 0.088 \qquad w_{a} = -1.09^{+0.31}_{-0.27}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.8\sigma}}
\underbrace{
w_{0} = -0.752 \pm 0.057 \qquad w_{a} = -0.86^{+0.23}_{-0.20}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 4.2\sigma}}
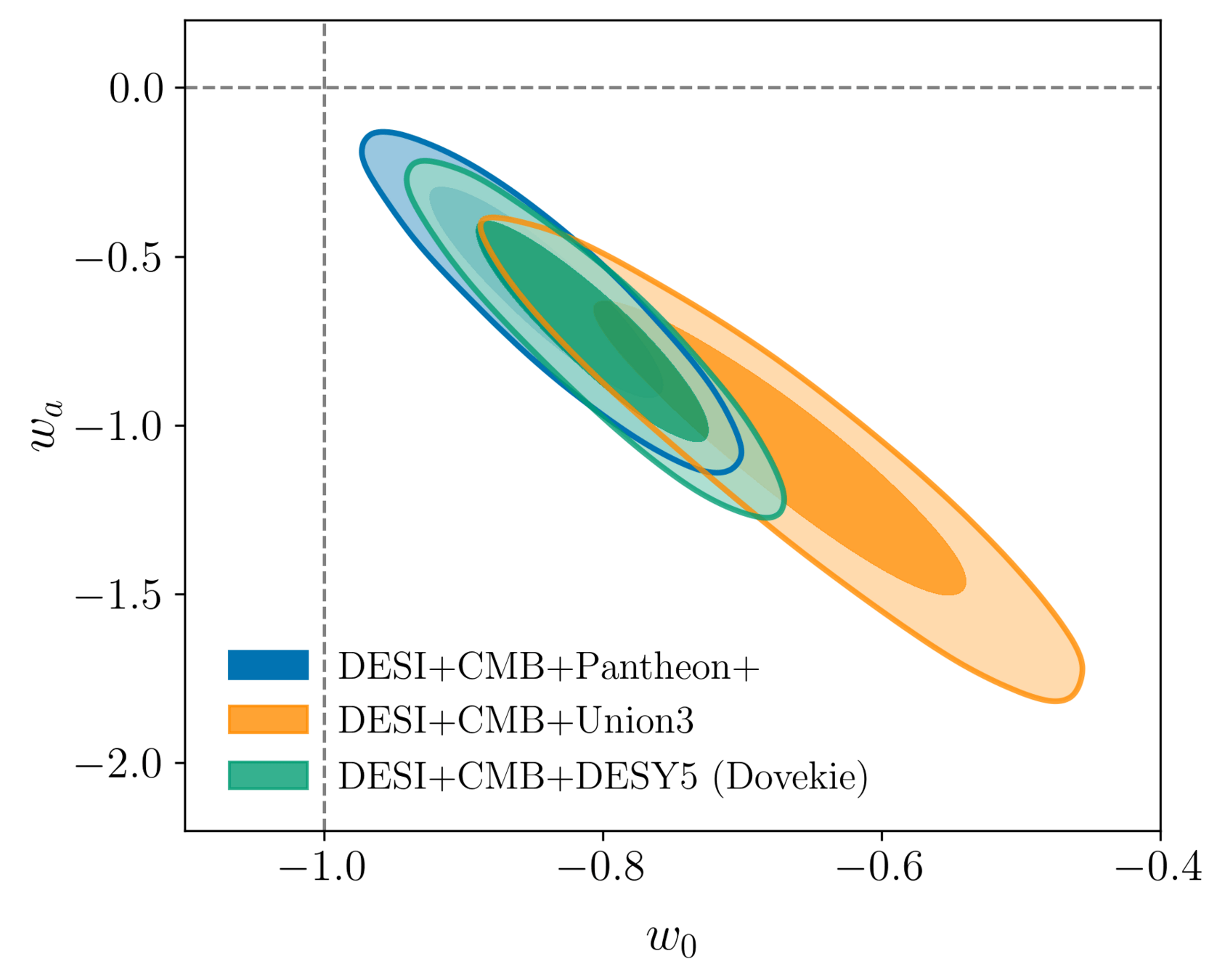
Dovekie \(3.3\sigma\)
Dark Energy EoS (with SN)
Robustness tests
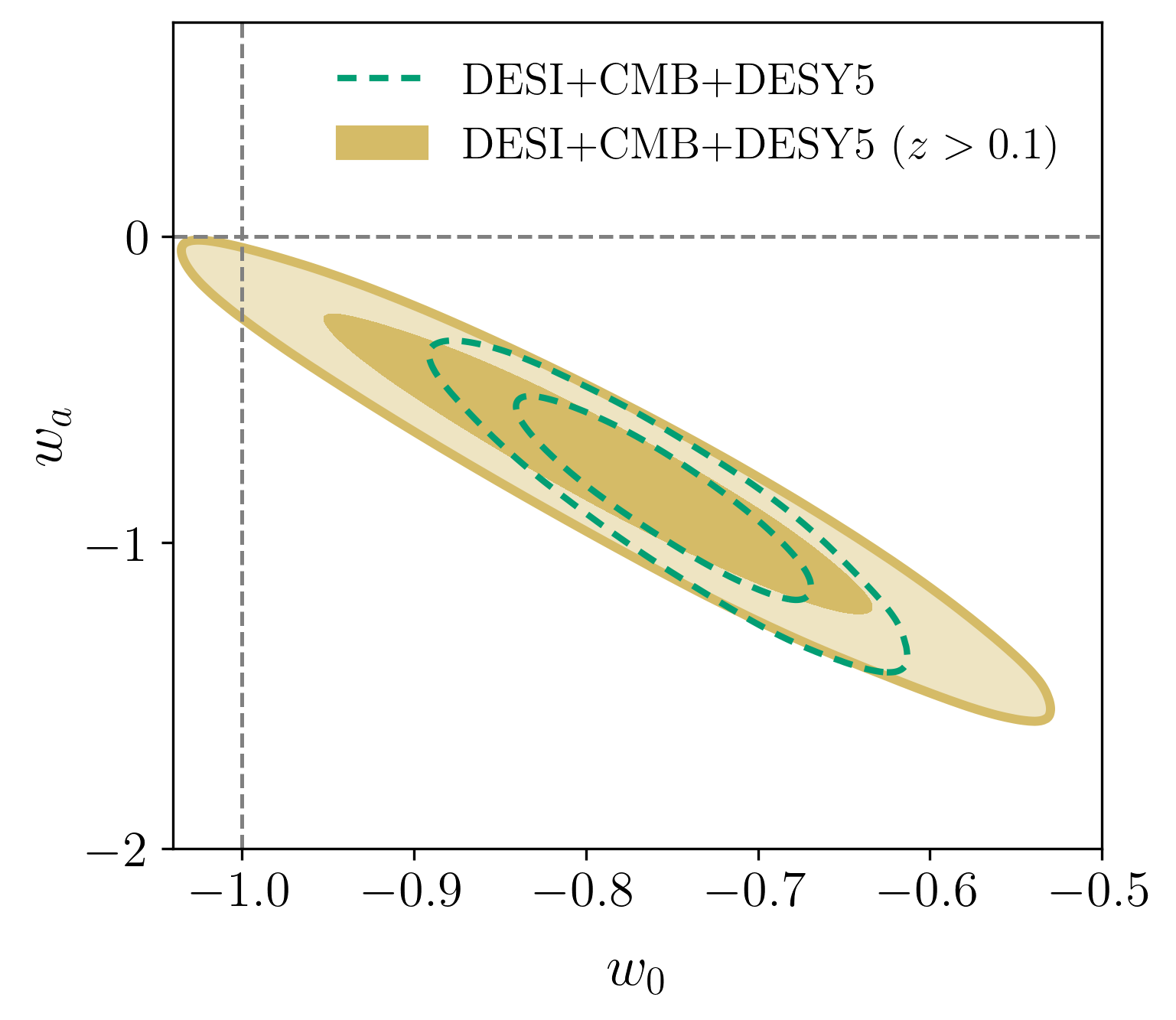
Removing low-\(z\) SN
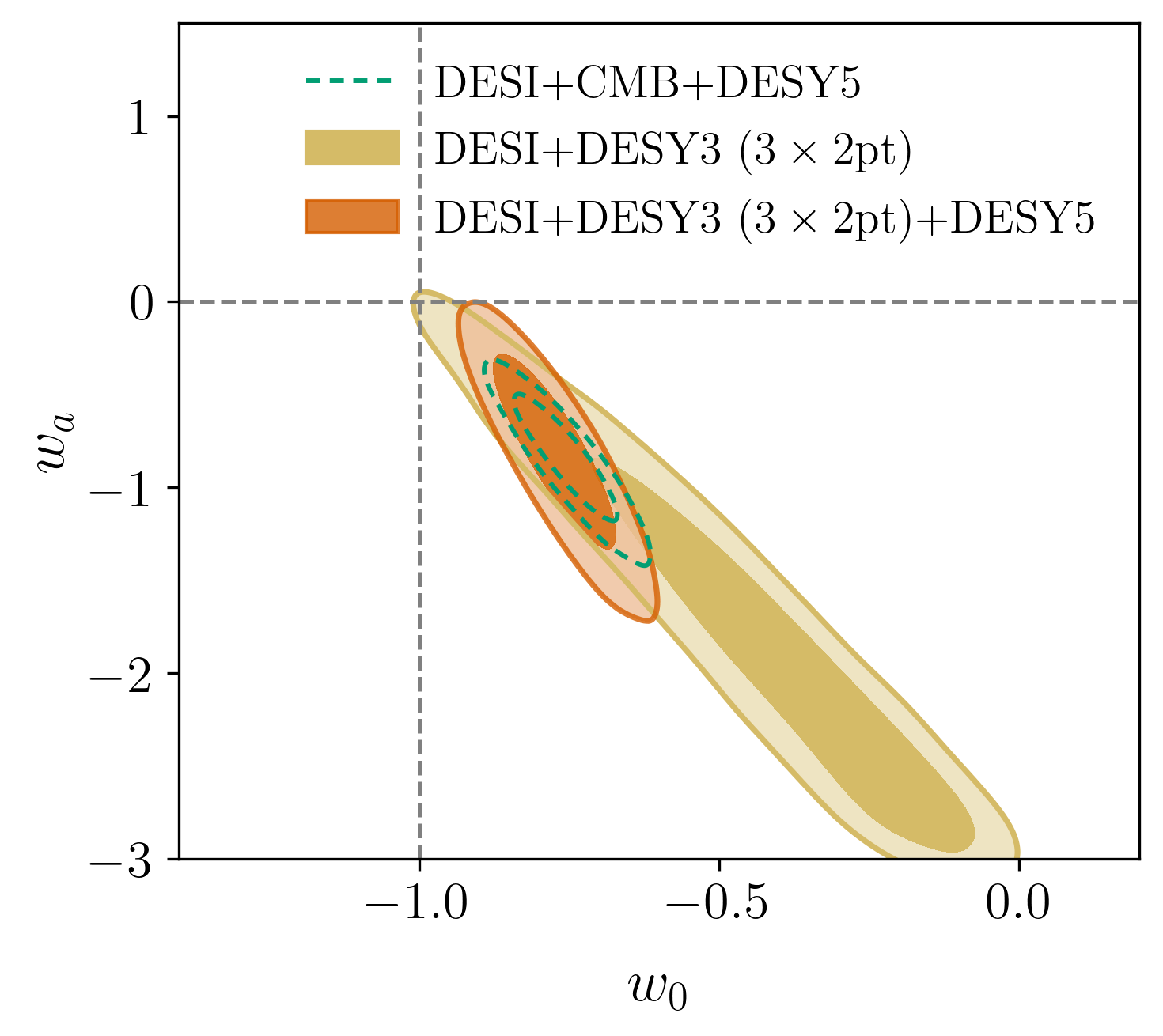
"Replacing CMB": DESY3 \(3\times2\)pt
\(3.3\sigma\)
Understanding tensions
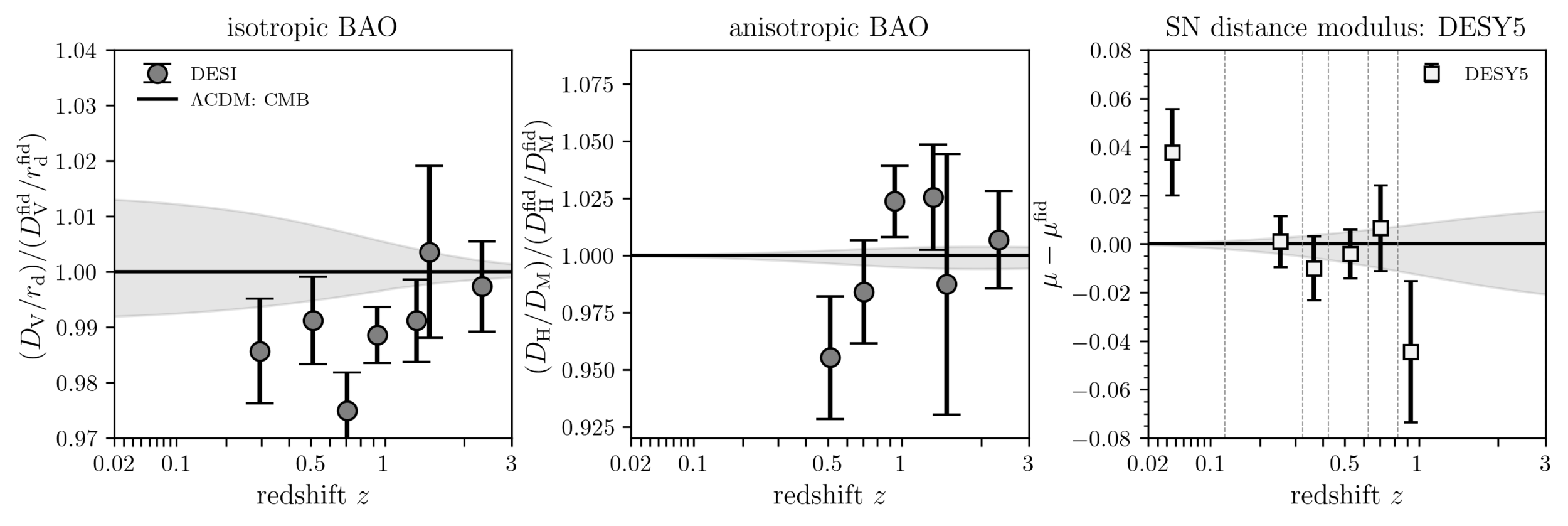
Understanding tensions
doesn't fit the SN!
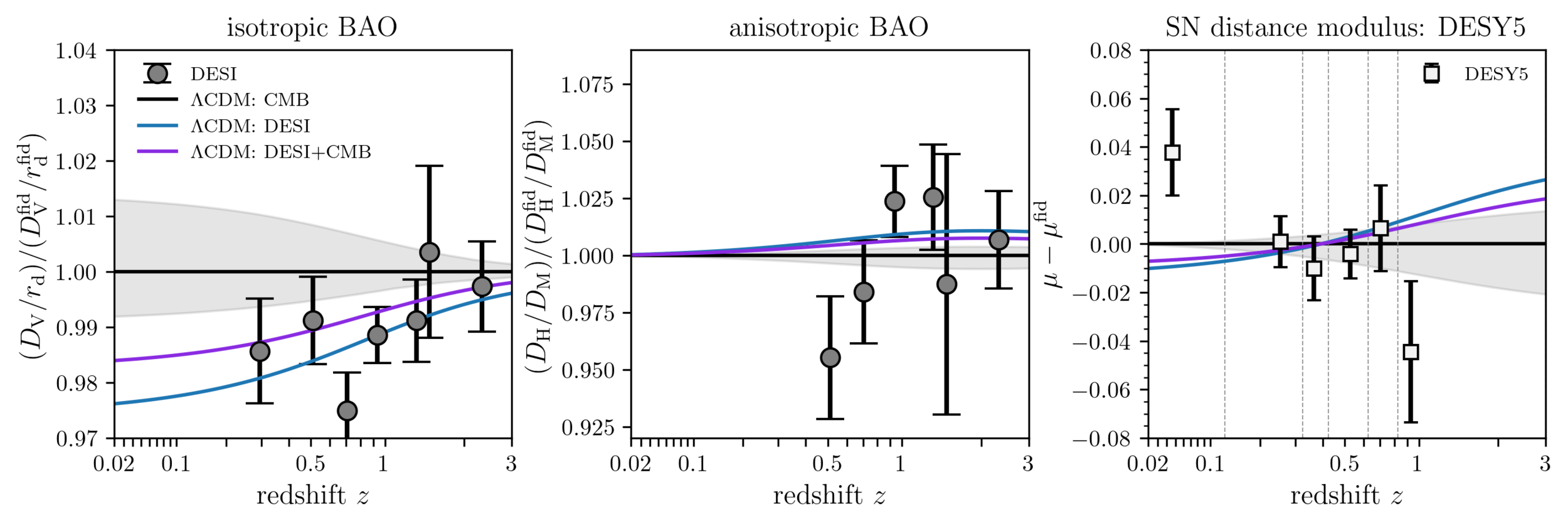
Understanding tensions
doesn't fit the BAO!
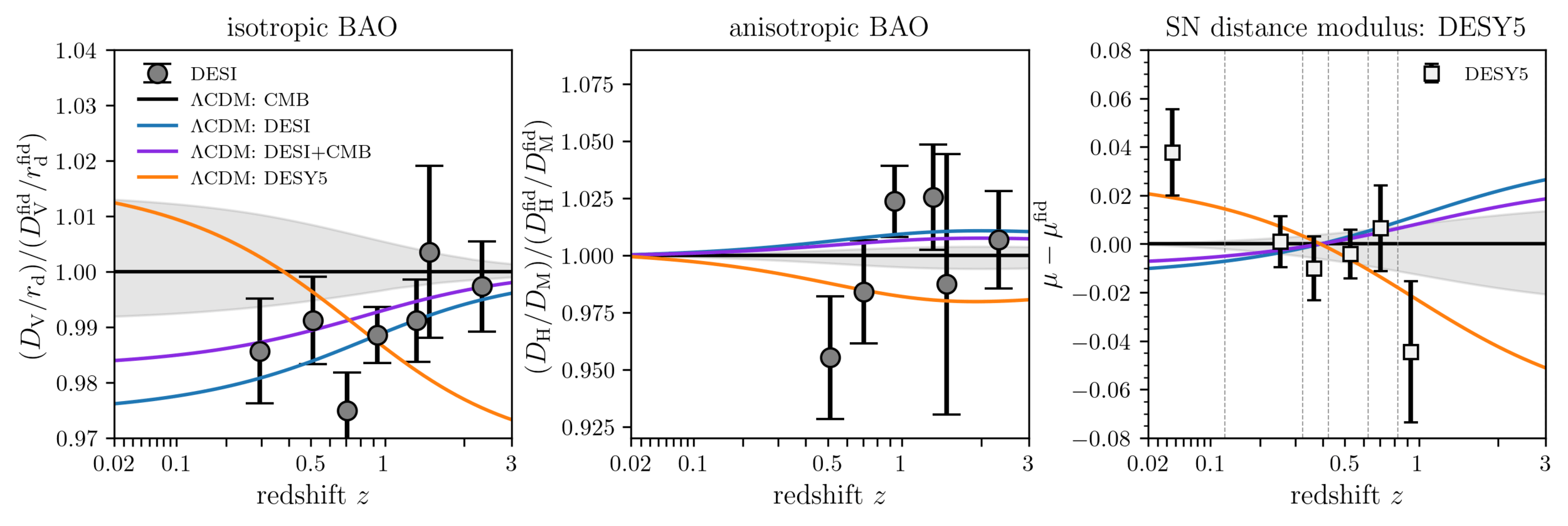
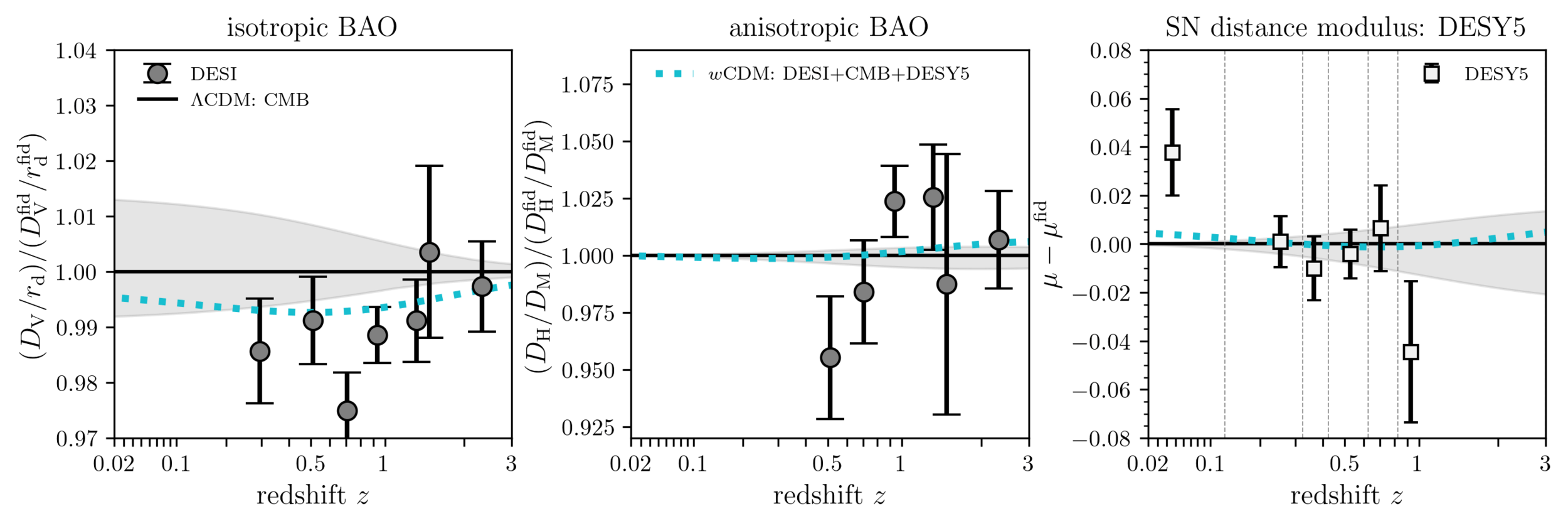
Understanding tensions
\(w\mathrm{CDM}\) not flexible enough to fit all 3 datasets!
w = -0.970
Understanding tensions
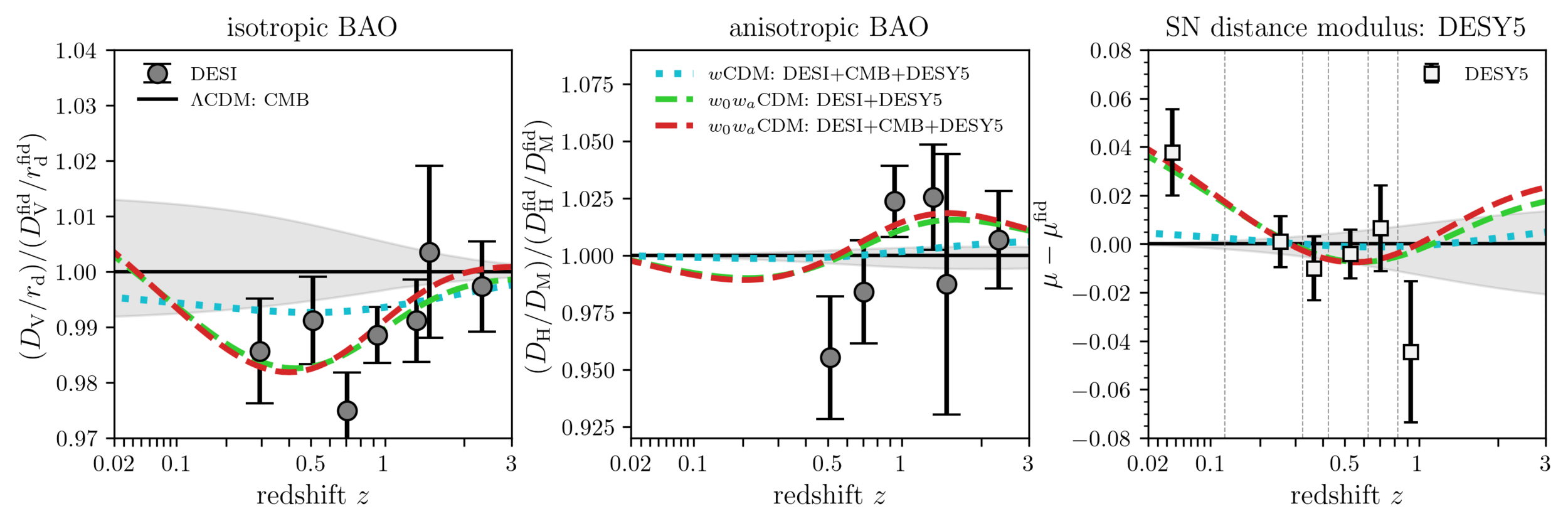
\(w_0w_a\mathrm{CDM}\) fits all 3 datasets!
Understanding tensions
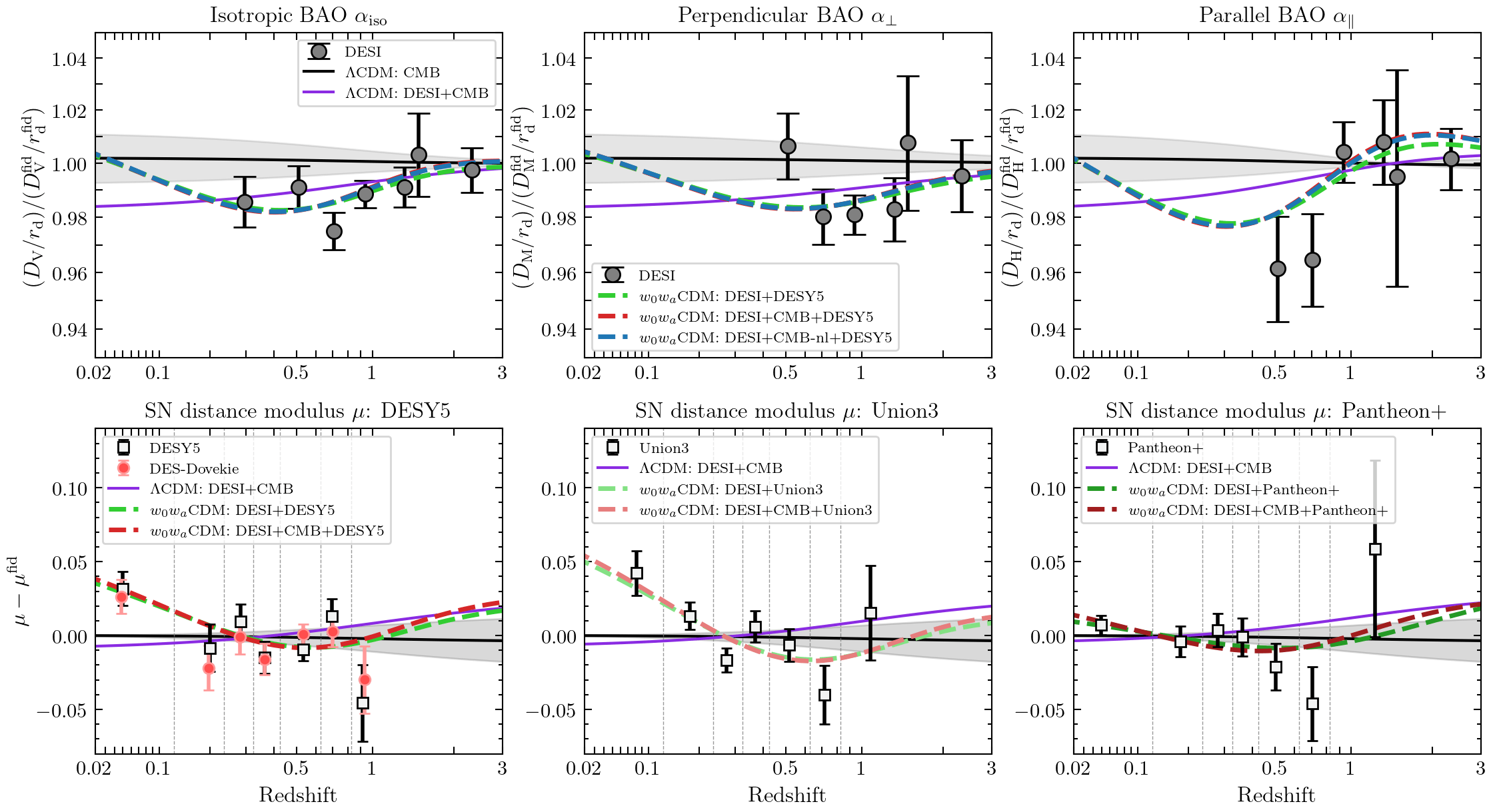
Dark Energy Evolution (\(w_0w_a\mathrm{CDM}\))
q(z)\equiv{-\frac{\ddot{a}a}{\dot{a}^2}}=\frac{d\ln H}{d\ln(1+z)}-1
Om(z)\equiv\frac{h^2(z)-1}{(1+z)^3-1}
f_{\rm DE}(z) \equiv \frac{\rho_\mathrm{DE}(z)}{\rho_\mathrm{DE,0}}
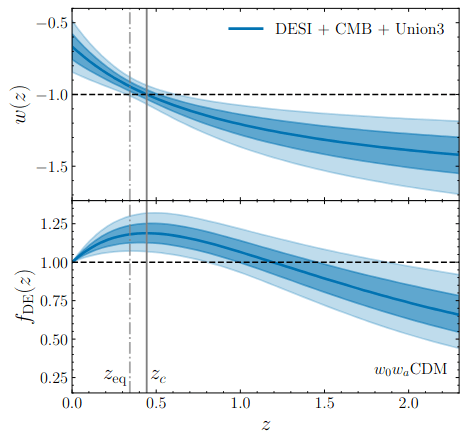
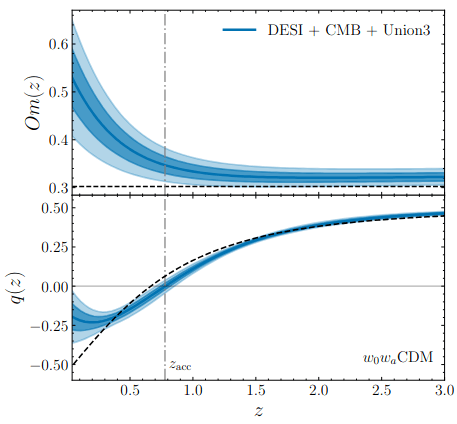
phantom
Dark Energy Evolution
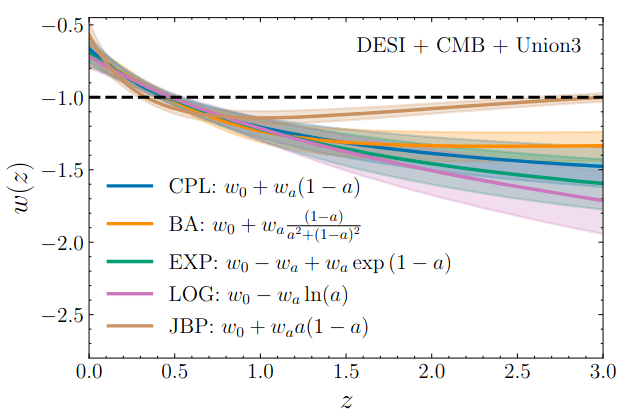
best described by CPL
\(4\sigma\)
Also considered: Gaussian Processes, similar evolution obtained
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO
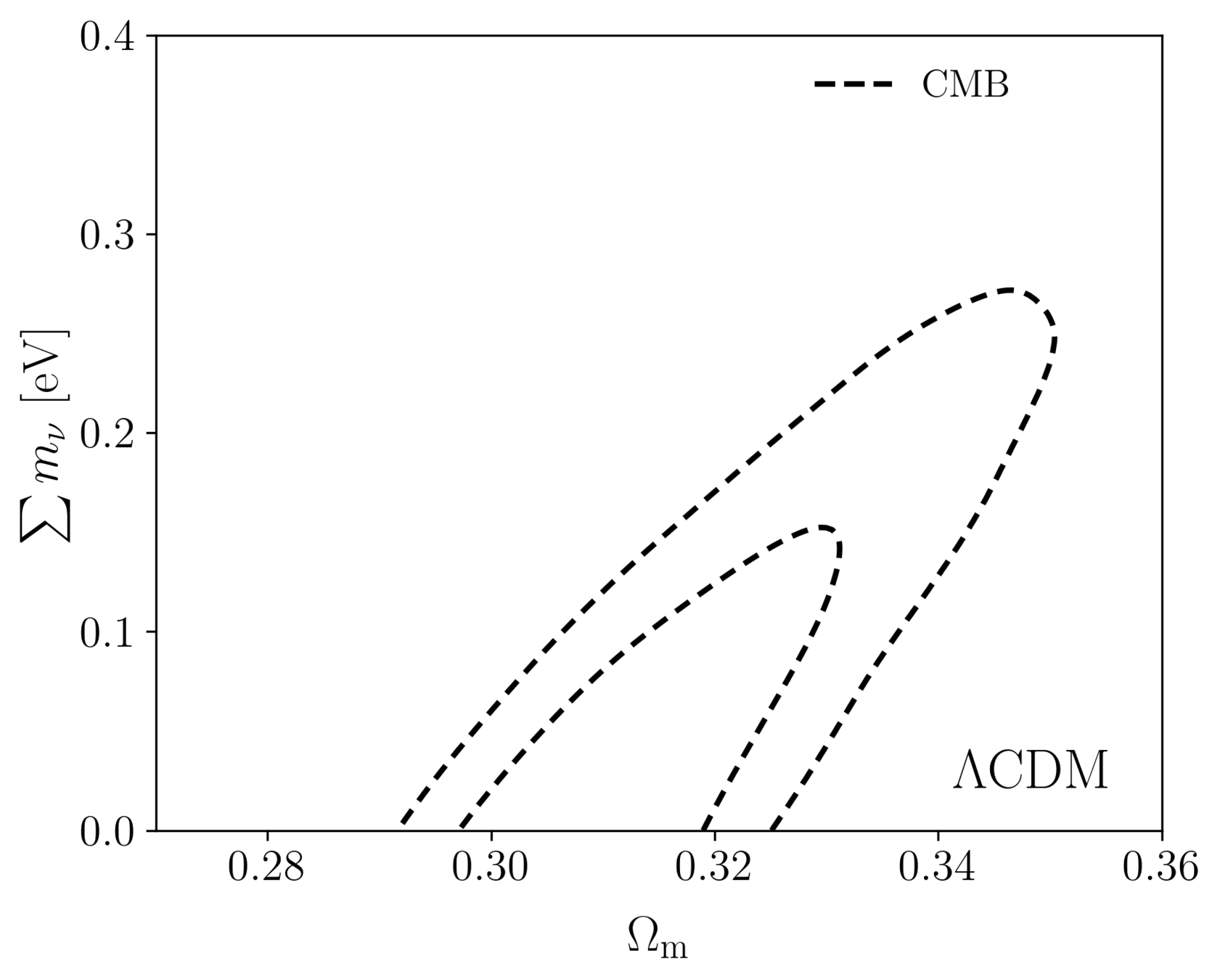
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
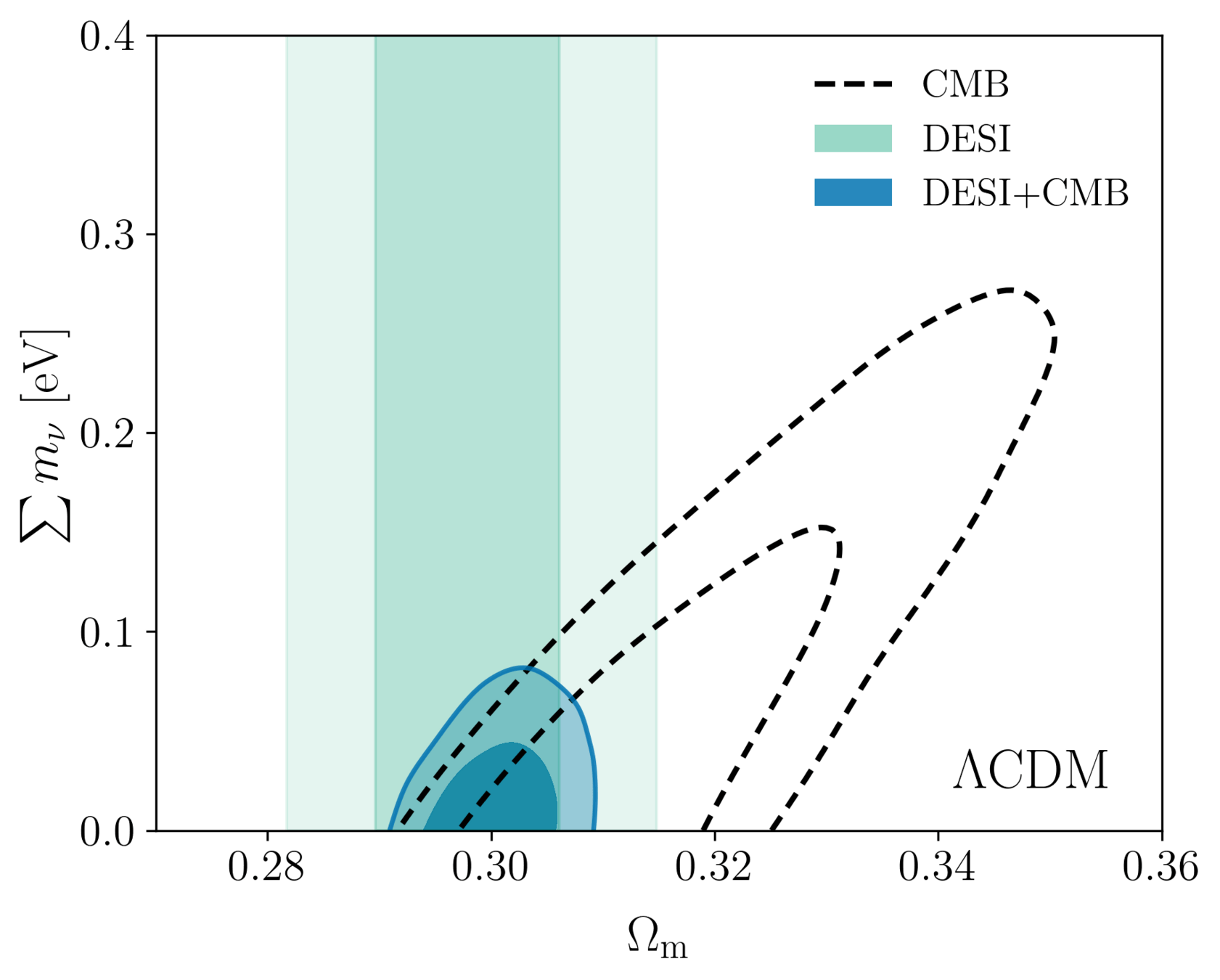
Broken by BAO, which favors low \(\Omega_\mathrm{m}\)
\sum m_\nu < 0.064 \, \mathrm{eV} \; (95\%, \text{DESI + CMB})
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO, which favors low \(\Omega_\mathrm{m}\)
\sum m_\nu < 0.064 \, \mathrm{eV} \; (95\%, \text{DESI + CMB})
Limit relaxed for \(w_0w_a\mathrm{CDM}\):
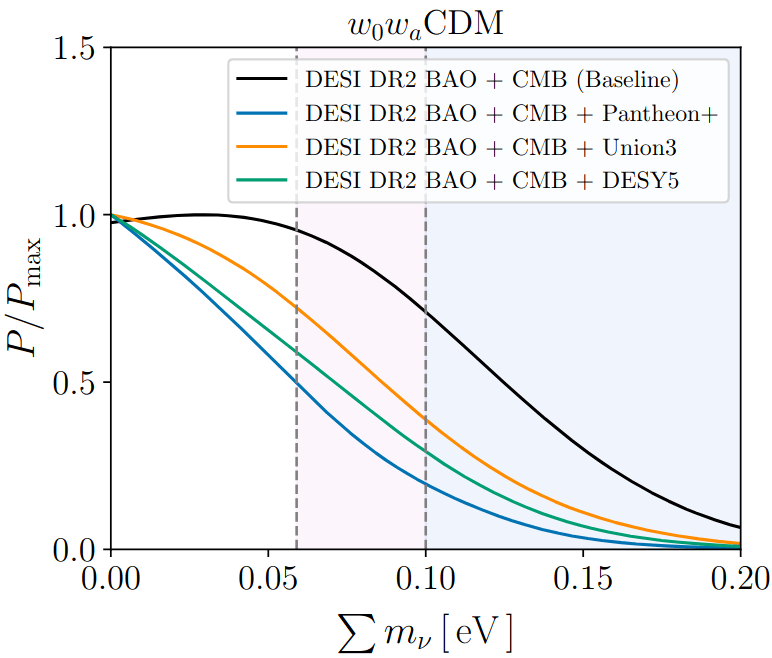
DESI+CMB: \(\sum m_\nu < 0.163 \, \mathrm{eV} \; (95\%)\)
DESI+CMB+DESY5: \(< 0.129 \, \mathrm{eV} \; (95\%)\)
Summary
DESI already has the most precise BAO measurements ever (40% more precise than DR1)
DESI in mild, growing, tension with CMB (\(2 - 3.7\sigma\)) and SN \((\sim 2\sigma)\) when interpreted in the ΛCDM model
Evidence for time-varying Dark Energy equation of state has increased with the DR2 BAO data by \(0.3\sigma\): CMB: \(3.1\sigma\), SN: \(2.8 - 3.8\sigma\), resolves \(\sum m_\nu\) tension
Evolving DE?
Phantom crossing isn't very natural. Can be achieved with:
- multifield \(\Rightarrow\) complex, fine-tuning
- non-minimal coupling between scalar field and gravity (e.g. Wolf+25)
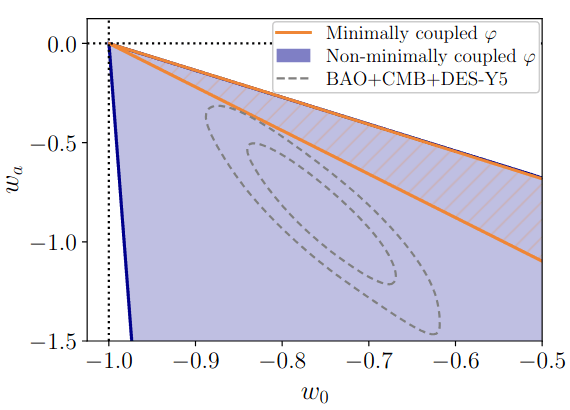
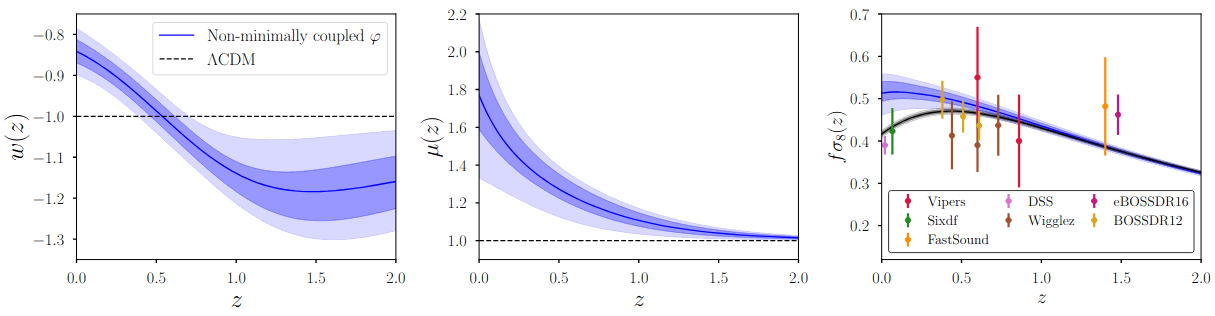
Evolving DE?
Phantom crossing isn't very natural. Can be achieved with:
- multifield \(\Rightarrow\) complex, fine-tuning
- non-minimal coupling between scalar field and gravity (e.g. Wolf+25)
- but the effect would be visible in structure growth
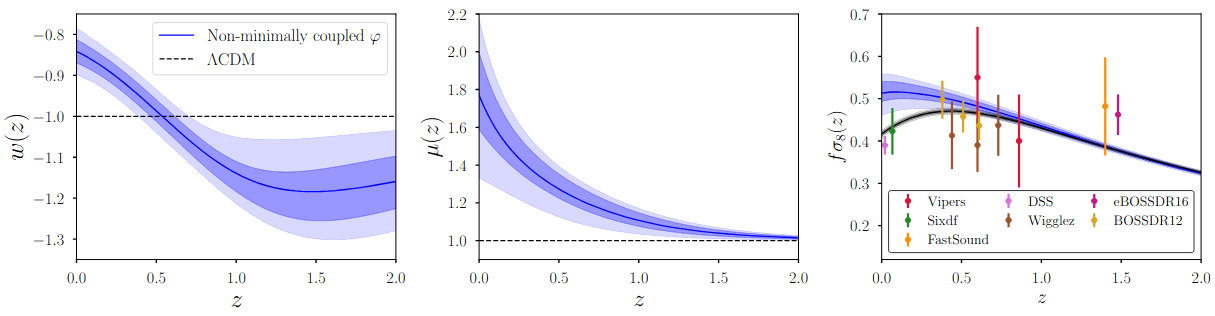
Evolving DE?
Phantom crossing isn't very natural. Can be achieved with:
- multifield \(\Rightarrow\) complex, fine-tuning
- non-minimal coupling between scalar field and gravity (e.g. Wolf+25)
- but the effect would be visible in structure growth
- coupling between DE and DM?
- but shifting \(w_\mathrm{DE}^\mathrm{eff}\) requires shifting \(w_\mathrm{m}^\mathrm{eff}\) in the opposite direction \(\Rightarrow\) difficult for structure growth
- maybe tilting (sign of interaction changing with time) dark energy? see Linder 2025 for complete discussion
Systematics?
Optical depth \(\tau\) (unlikely?)
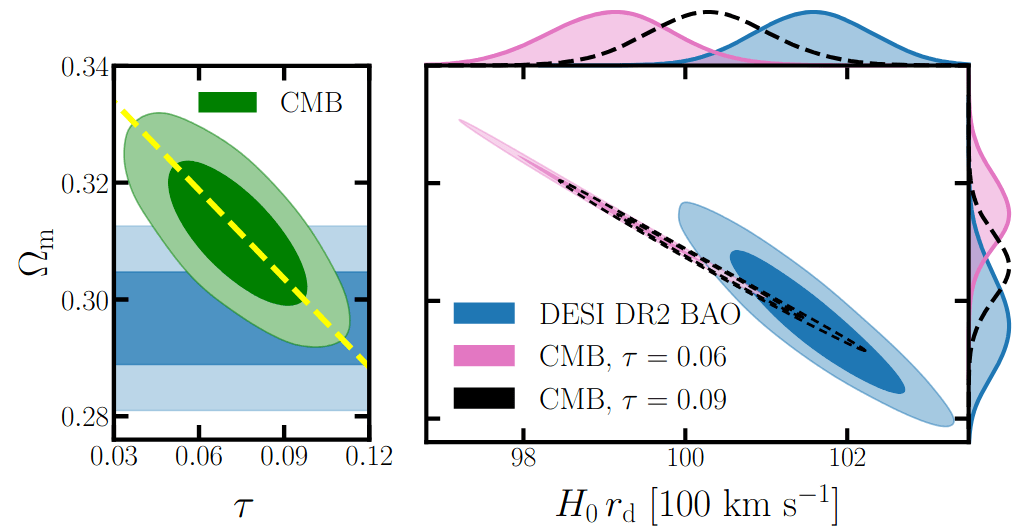
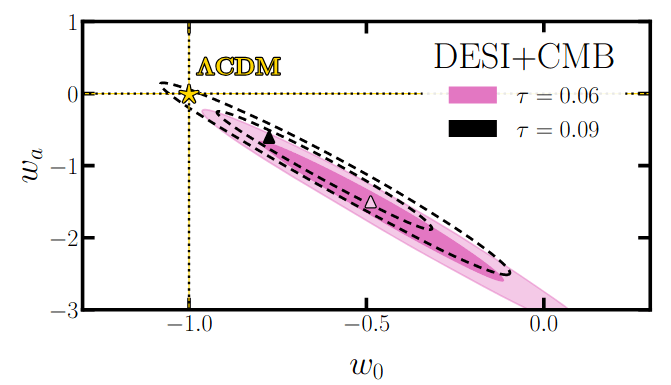
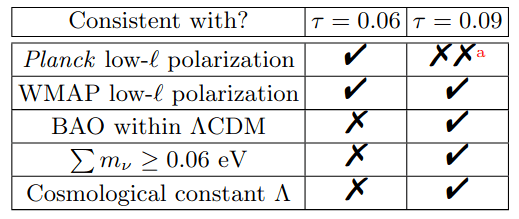
\(\tau = 0.09\) \(3\sigma \Rightarrow 1.5\sigma\) for \(w_0w_a\mathrm{CDM}\)
3-5\(\sigma\) tension in low-\(\ell\) Planck polarization
Strengthens the case for future CMB experiments
\(3\sigma \Rightarrow 1.5\sigma\)
Systematics in BAO? (unlikely!)
- Observational systematics have basically no effect on BAO
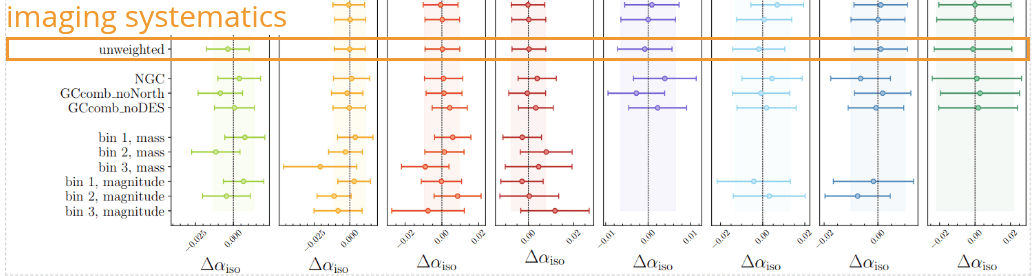
- Theoretical systematics? \(<0.1\% - 0.2\%\), see Chen+24
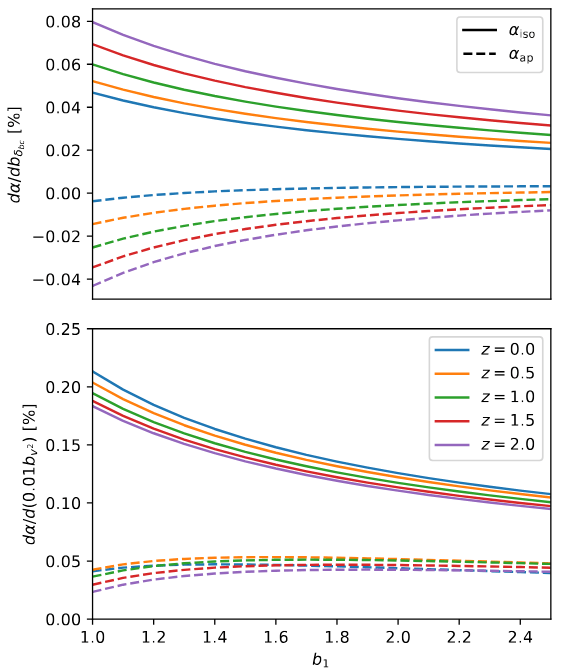
bias between dark matter and baryons
IPhT_December2025
By Arnaud De Mattia
