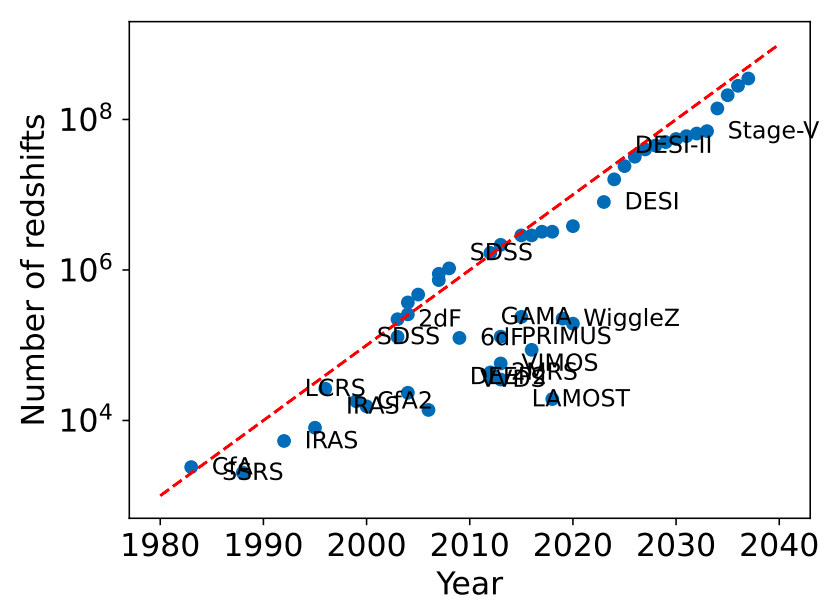
DESI DR2: Survey Overview,
BAO Cosmological Constraints
Preparation for Full-Shape Analyses
Arnaud de Mattia
CEA Paris-Saclay, Irfu
Waterloo, November 5th
What I'm going to talk about
- The DESI survey
- The DR2 BAO analysis
- The cosmological constraints
- On-Going: DR2 Full Shape analysis
- My interests & my projects
\(\simeq 34\) min
\(\simeq 15\) min
from pathlib import Path
import lsstypes as types
dirname = Path('/global/cfs/projectdirs/desi/mocks/cai/mock-challenge-cutsky-dr2/summary_statistics/cutsky/abacus-2ndgen-complete/')
spectrum = types.read(dirname / 'mesh2_spectrum_poles_LRG_z0.4-0.6_NGC_0.h5')
spectrum = spectrum.select(k=slice(0, None, 5)).select(k=(0, 0.2)) # rebin, select 0 < k < 0.2 h/Mpc
window = types.read(dirname / 'window_mesh2_spectrum_poles_LRG_z0.4-0.6_NGC.h5')
window = window.at.observable.match(spectrum) # rebin "observable" axis to match observable spectrum
print(window.observable)
print(window.theory)
window.value() # access to 2D window (observable, theory)
covariance = types.read(dirname / 'covariance_mesh2_spectrum_poles_LRG_z0.4-0.6_NGC.h5')
covariance = covariance.at.observable.match(spectrum)
covariance.value() # access to 2D covariance
Thanks to our sponsors and
72 Participating Institutions!
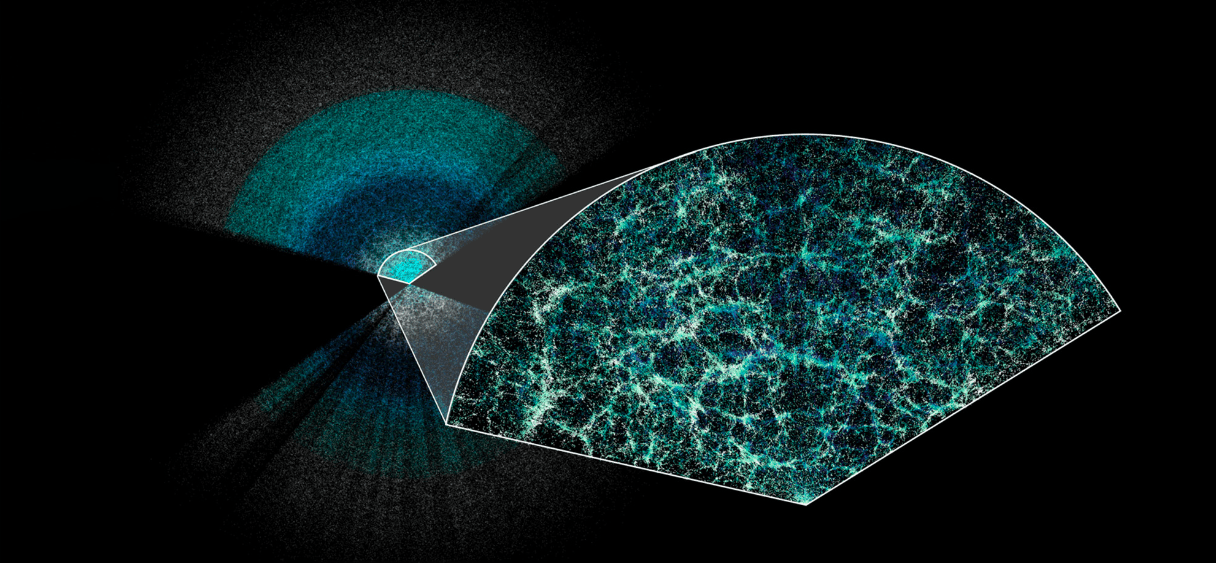
DESI 3D Map
Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z
DESI 3D Map
Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z
DESI: a stage IV survey
10 years = \(10 \times \)
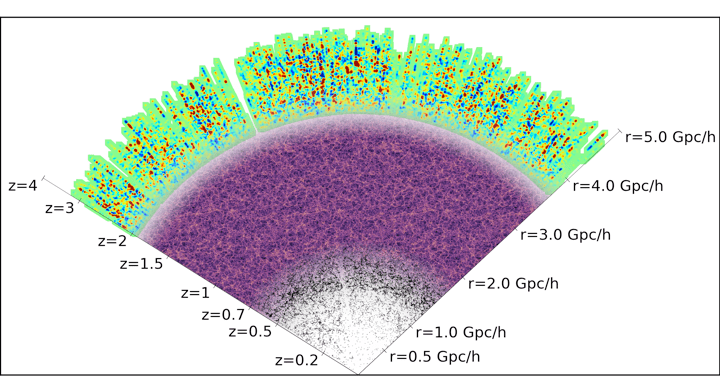
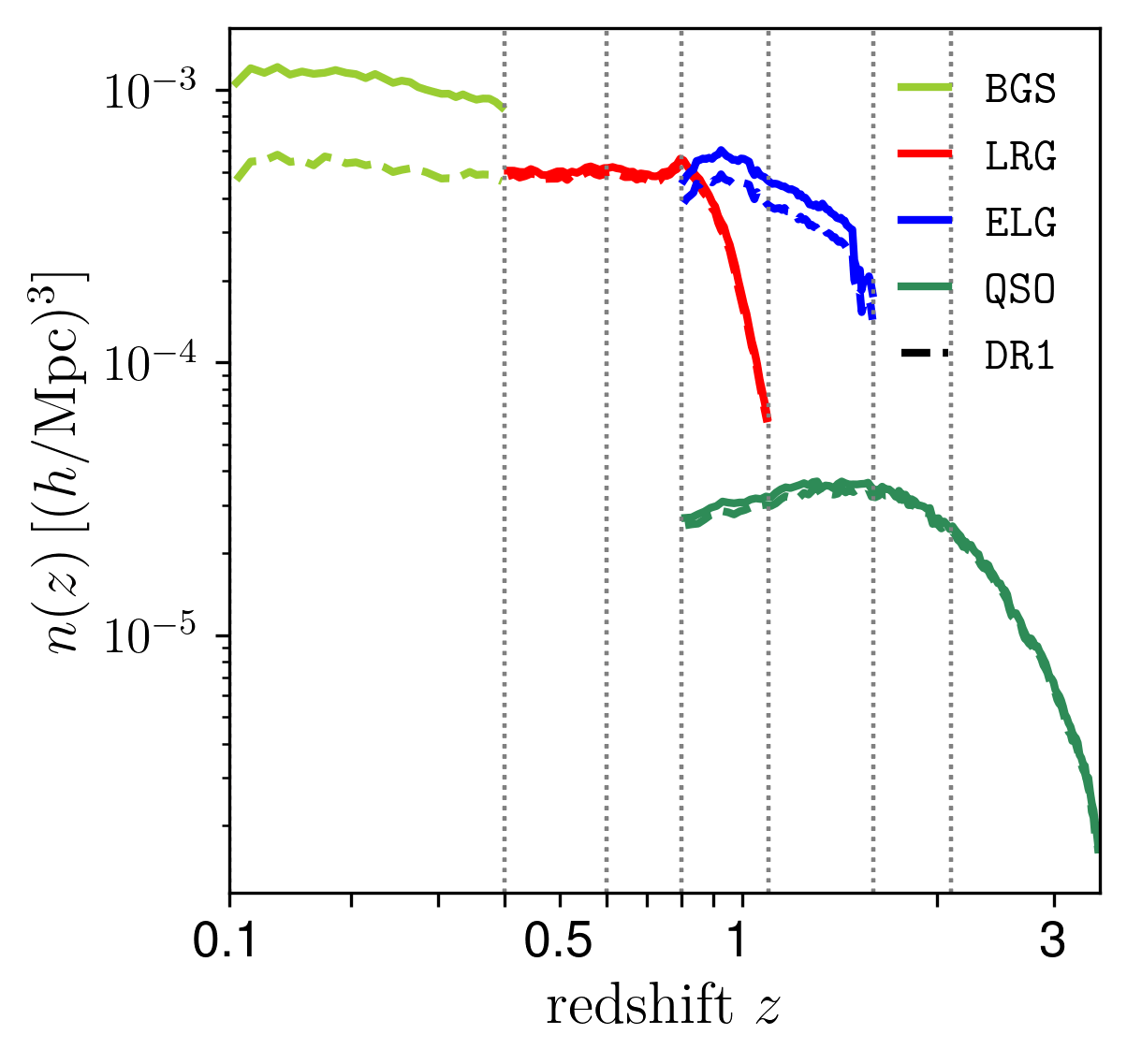
DESI Y5 galaxy samples
Bright Galaxies: 14M (SDSS: 600k)
0 < z < 0.4
LRG: 8M (SDSS: 1M)
0.4 < z < 1.1
ELG: 16M (SDSS: 200k)
0.6 < z < 1.6
QSO: 3M (SDSS: 500k)
Ly\(\alpha\) \(1.8 < z\)
Tracers \(0.8 < z < 2.1\)
Y5 (DR1-DR2-DR3) \(\sim 40\)M galaxy redshifts!
\(z = 0.4\)
\(z = 0.8\)
\(z = 0\)
\(z = 1.6\)
\(z = 2.0\)
\(z = 3.0\)
From images to redshifts
imaging surveys (2014 - 2019) + WISE (IR)
target selection
spectroscopic observations
spectra and redshift measurements
Mayall Telescope
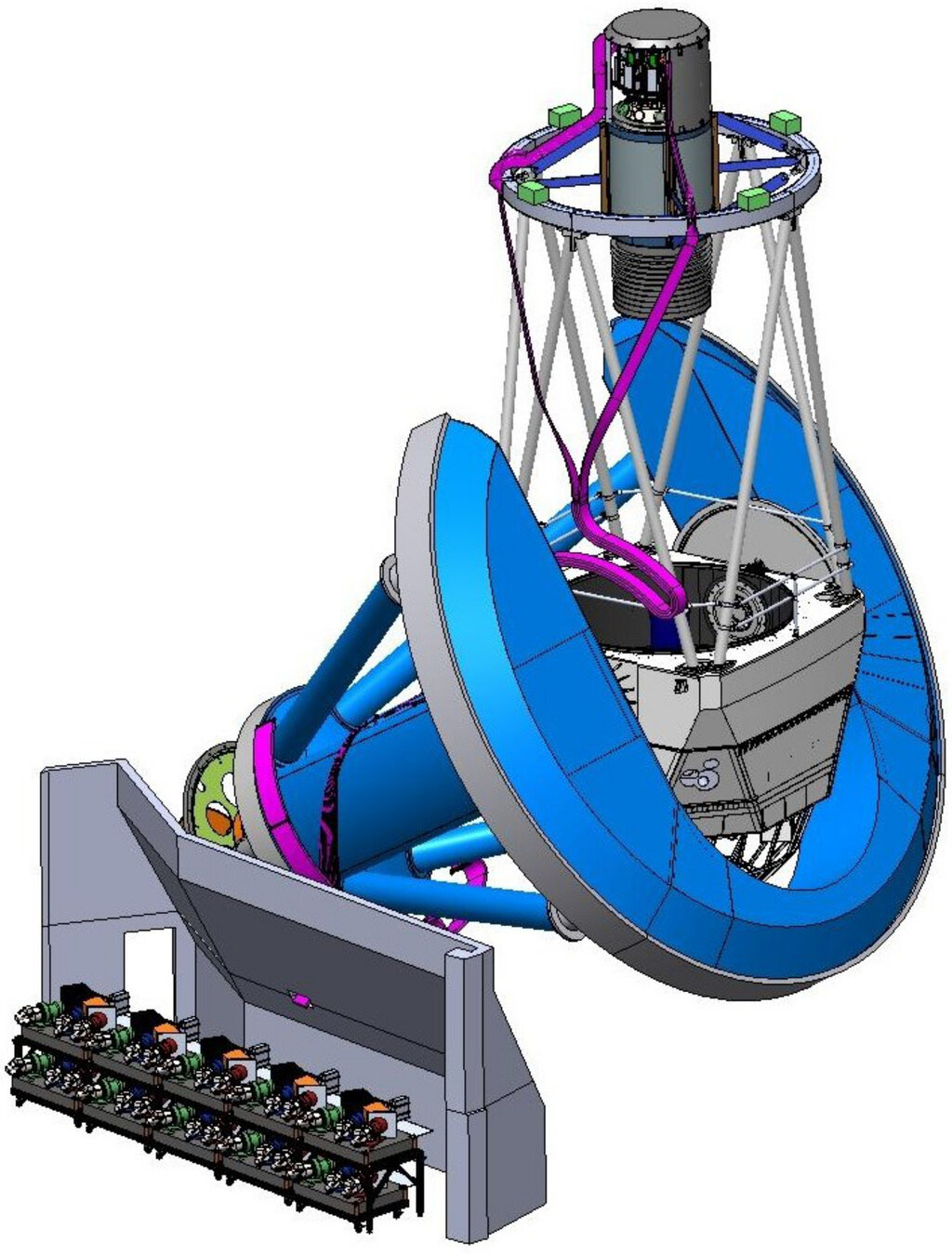
focal plane 5000 fibers
wide-field corrector
6 lenses, FoV \(\sim 8~\mathrm{deg}^{2}\)
Kitt Peak, AZ
4 m mirror
Mayall Telescope
focal plane 5000 fibers
fiber view camera
ten 3-channel spectrographs
49 m, 10-cable fiber run
Kitt Peak, AZ
Focal plane: 5000 robotic positioners
86 cm
Focal plane: 5000 robotic positioners
Exposure time (dark): 1000 s
Configuration of the focal plane
CCD readout
Go to next pointing
140 s
0.1 mm
Spectroscopic pipeline
wavelength
fiber number
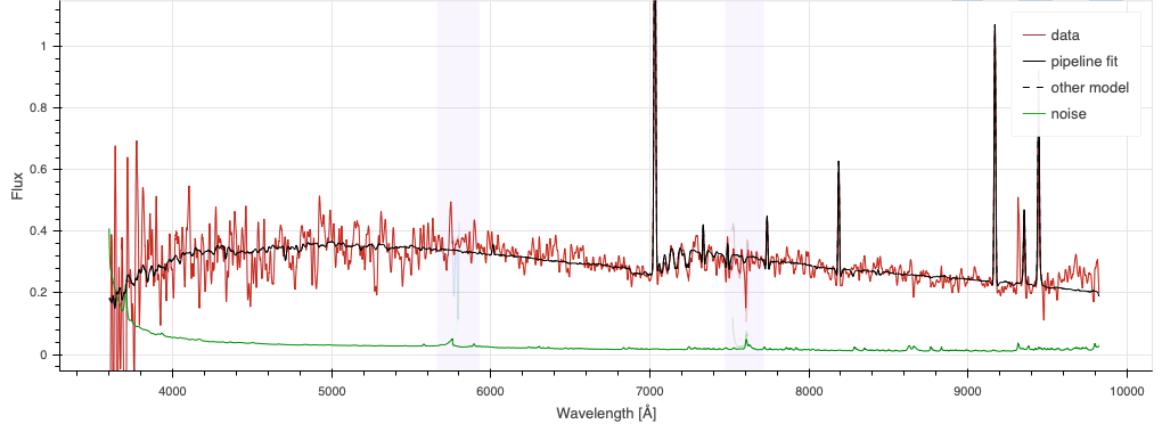
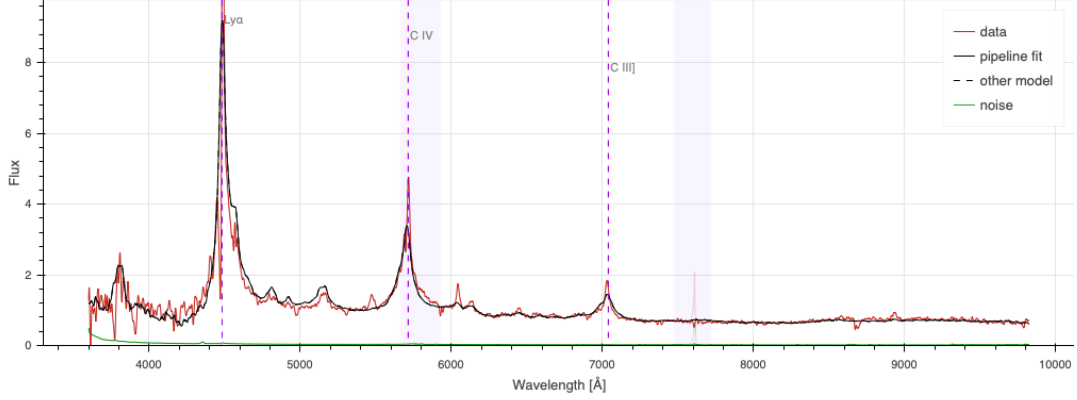
\(z = 2.1\) QSO
\(z = 0.9\) ELG
Ly\(\alpha\)
CIV
CIII
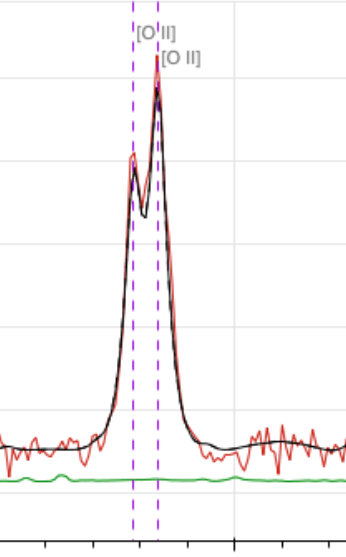
[OII] doublet at \(3727 \AA\) up to \(z = 1.6\)
[OII]
Ly\(\alpha\) at \(1216 \AA\) down to \(z = 2.0\)
DESI data release 2 (DR2)
Observations from May 14th 2021 to April 9th 2024
approved
construction started
first light
survey started
DR1 data sample
DR1 results
DR2 sample secured
DR3
DR2 results
Final survey
- dark time (LRG, ELG, QSO): 7 visits
- bright time (BGS): 5 visits
- 14,000 \(\mathrm{deg}^2\)
2015
16
17
18
19
20
22
23
24
21
25
26
27
DESI data release 2 (DR2)
- 30M galaxy and QSO redshifts in 3 years of operation
- 14M used in the DR2 analysis (6M in DR1)
- Including 820,000 Ly\(\alpha\) QSO at \(z > 2.09\) (420,000 in DR1)
- \(> 2\times\) increase in number of tracers
higher completeness (deeper)
extended mag cut
Release of DESI DR2 (BAO) results
March 19th 2025
First batch of DESI DR2 cosmological analyses: https://data.desi.lbl.gov/doc/papers/dr2
• DESI Collaboration et al. (2025), DESI DR2 Results I: Baryon Acoustic Oscillations from the Lyman Alpha Forest
• DESI Collaboration et al. (2025), DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints
Companion supporting papers:
Lodha et al. (2025), Extended Dark Energy analysis
Elbers et al. (2025), Constraints on Neutrino Physics
Andrade et al. (2025), Validation of the DESI DR2 BAO mesurements
Casas et al. (2025), Validation of the DESI DR2 Lyα BAO analysis using synthetic datasets
Brodzeller et al. (2025), Construction of the Damped Lyα Absorber Catalog for DESI DR2 Lyα BAO
DR1 public!
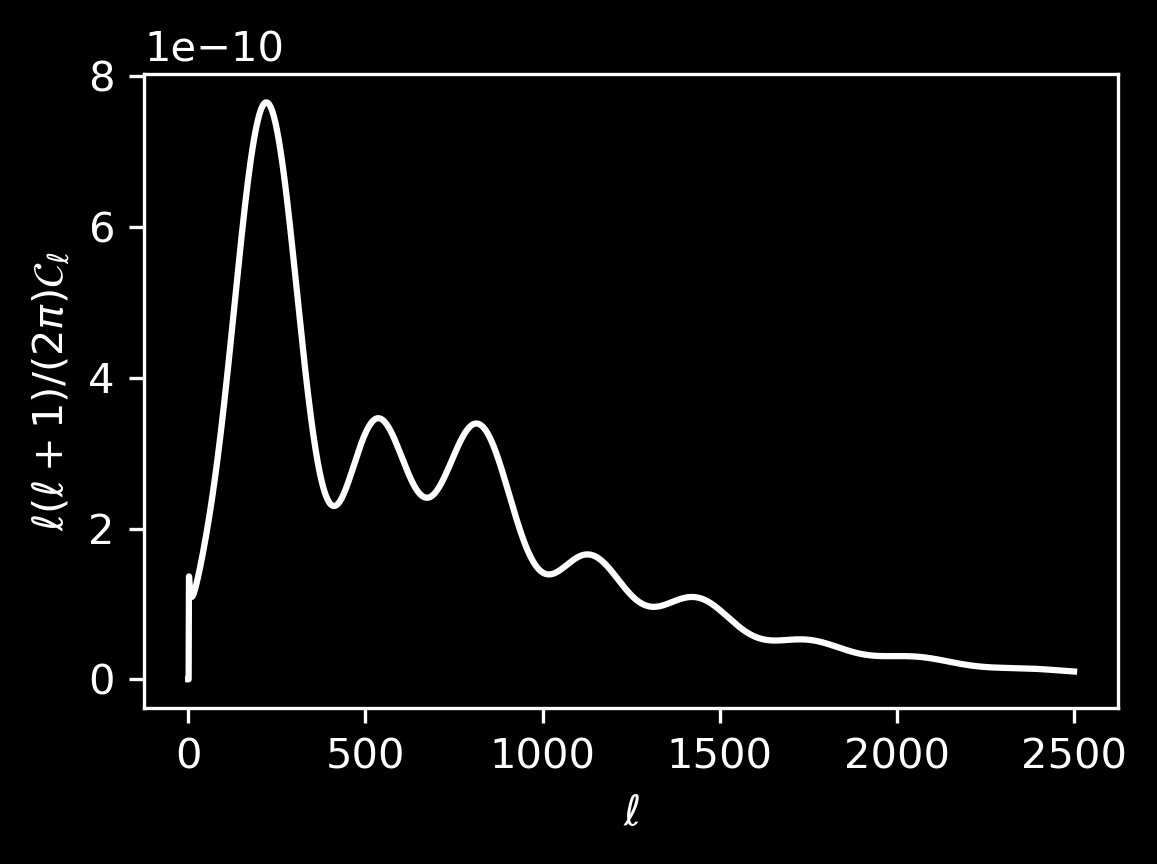
Baryon Acoustic Oscillations
Sound waves in primordial plasma
At recombination (\(z \simeq 1100\))
- plasma changes to optically thin
- baryons decouple from photons
- sound wave stalls after travelling \(r_\mathrm{d}\)
Sound horizon scale at the drag epoch
\(r_\mathrm{d} \simeq 150\; \mathrm{Mpc}\)
standard ruler
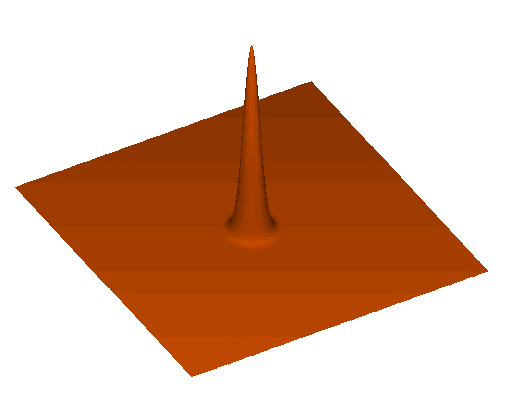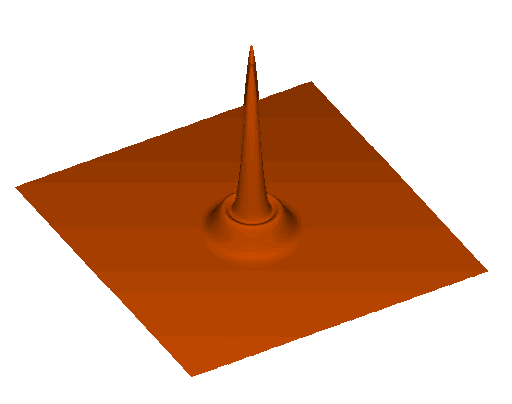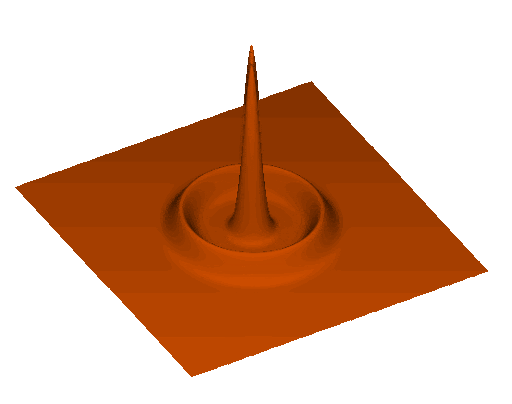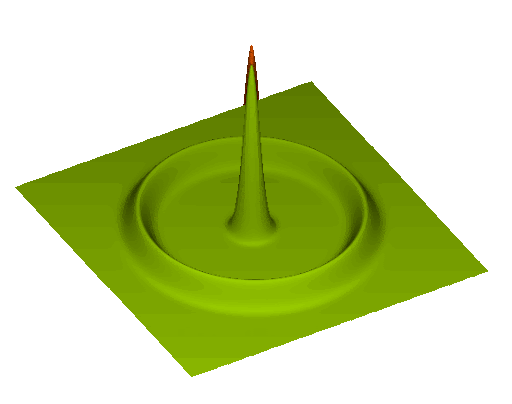
Baryon Acoustic Oscillations
CMB (\(z \simeq 1100\))
Sound waves in primordial plasma
At recombination (\(z \simeq 1100\))
- plasma changes to optically thin
- baryons decouple from photons
- sound wave stalls after travelling \(r_\mathrm{d}\)
Sound horizon scale at the drag epoch
\(r_\mathrm{d} \simeq 150\; \mathrm{Mpc}\)
standard ruler
CMB (\(z \simeq 1100\))
LSS
Baryon Acoustic Oscillations
BAO measurements
distribution of galaxies (cartoonish)
\theta_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{M}(z)
transverse comoving distance
sound horizon \(r_\mathrm{d}\)
- angle on the sky (transverse to the line-of-sight): \(\theta_\mathrm{BAO} = \orange{r_\mathrm{d}}/\green{D_\mathrm{M}(z)}\)
- \(\Delta z\) (along the line-of-sight): \( \Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z) = \green{H(z)} \orange{r_\mathrm{d}} / c \)
BAO measurements
distribution of galaxies (cartoonish)
\Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z)
Hubble distance \(c/H(z)\)
sound horizon \(r_\mathrm{d}\)
- angle on the sky (transverse to the line-of-sight): \(\theta_\mathrm{BAO} = \orange{r_\mathrm{d}}/\green{D_\mathrm{M}(z)}\)
- \(\Delta z\) (along the line-of-sight): \( \Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z) = \green{H(z)} \orange{r_\mathrm{d}} / c \)
BAO measurements
- angle on the sky (transverse to the line-of-sight): \(\theta_\mathrm{BAO} = \orange{r_\mathrm{d}}/\green{D_\mathrm{M}(z)}\)
- \(\Delta z\) (along the line-of-sight): \( \Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z) = \green{H(z)} \orange{r_\mathrm{d}} / c \)
- at multiple redshifts \(z\)
Probes the expansion history (\(\green{D_\mathrm{M}, D_H}\)), hence the energy content (e.g. dark energy)
Absolute size at \(z = 0\): \(H_0 \orange{r_\mathrm{d}}\)
z_1
z_2
z_3
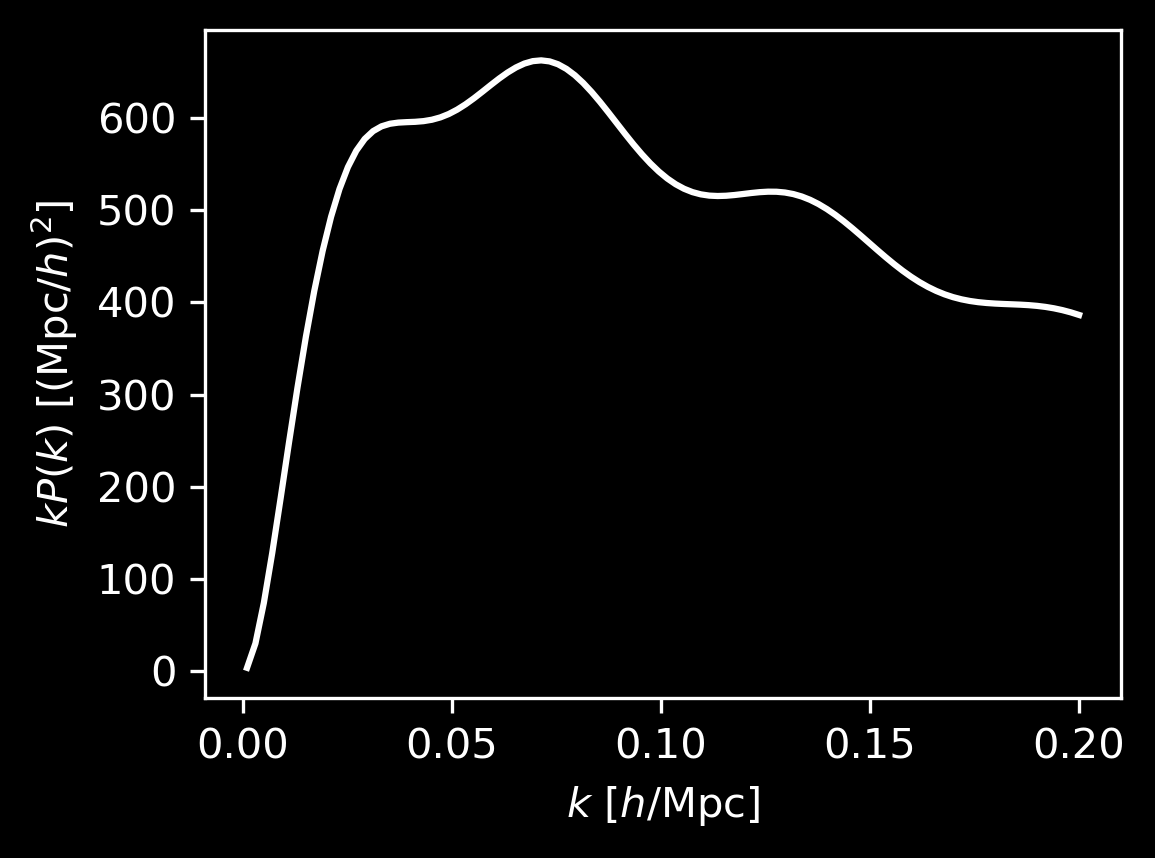
BAO measurements
correlation function
BAO peak
line of sight
monopole
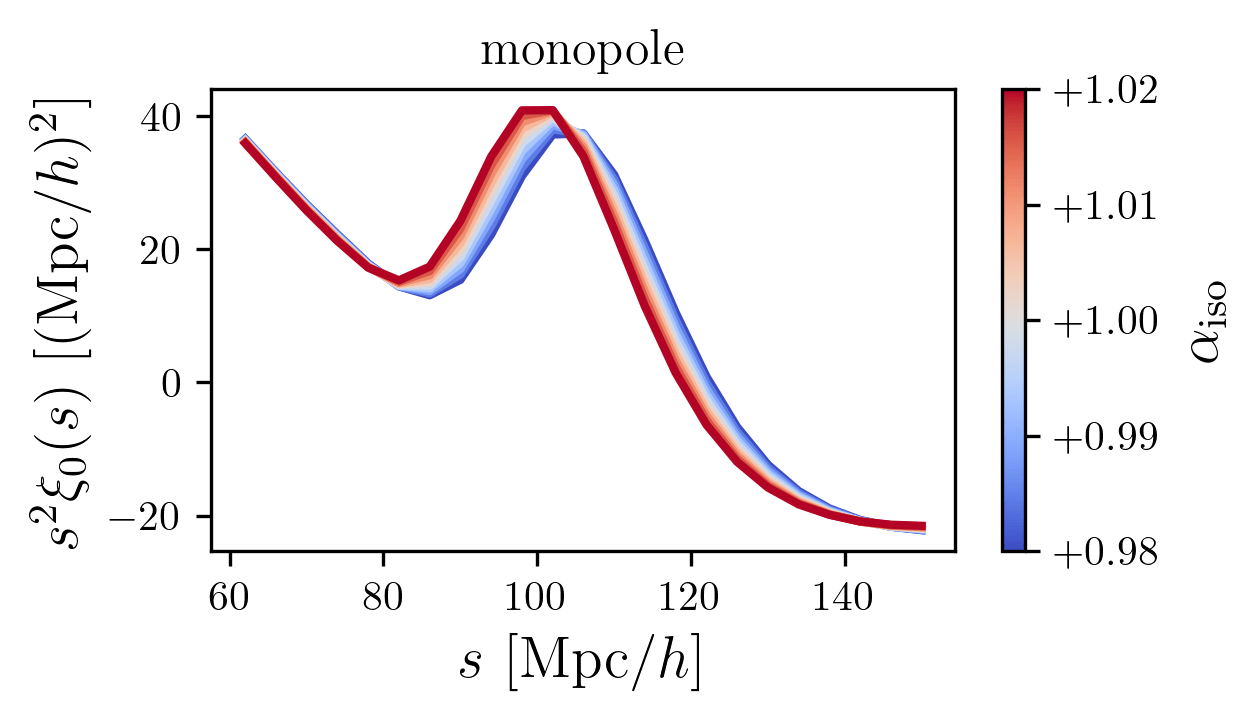
BAO measurements
correlation function
\alpha_\mathrm{iso} \propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
BAO peak
line of sight
monopole
isotropic
comoving transverse distance
Hubble distance \(c/H(z)\)
sound horizon (standard ruler)
BAO measurements
isotropic
anisotropic
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)
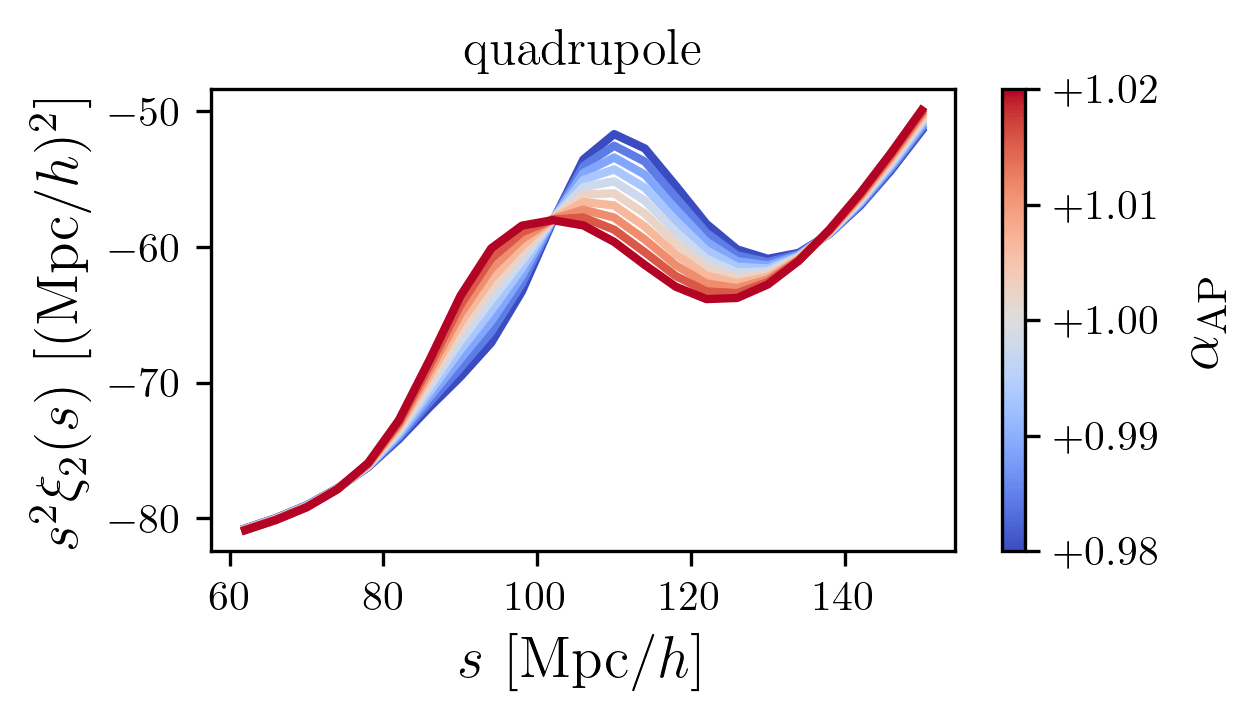
BAO peak
line of sight
line of sight
monopole
quadrupole
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
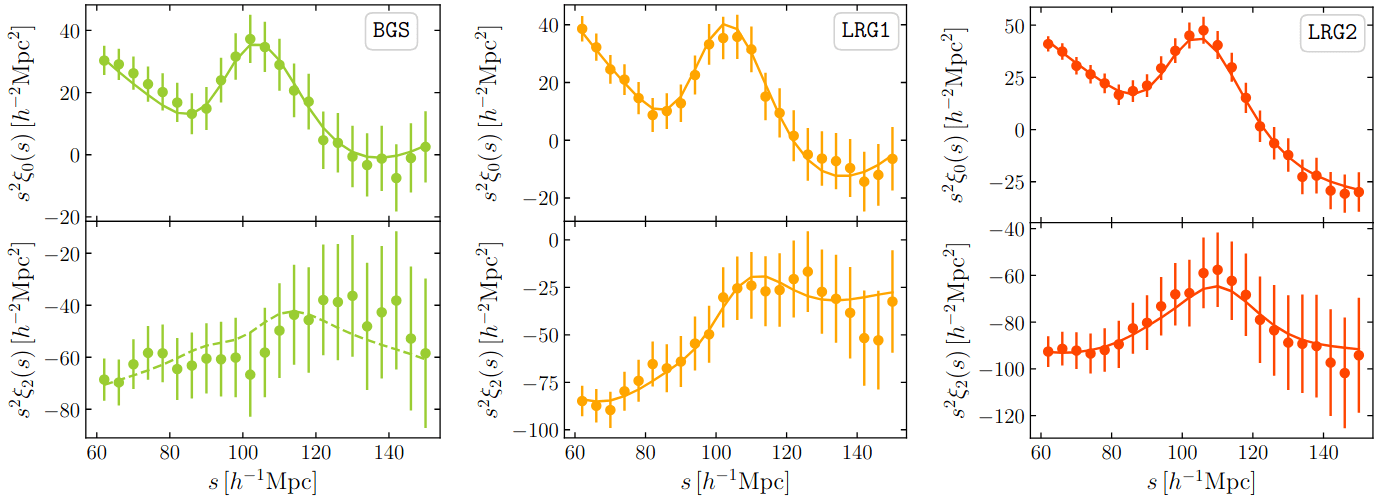
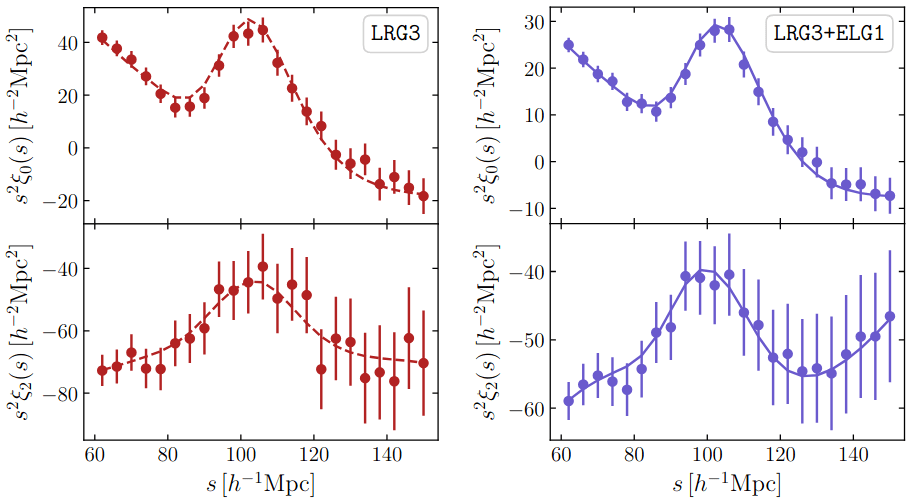
low S/N
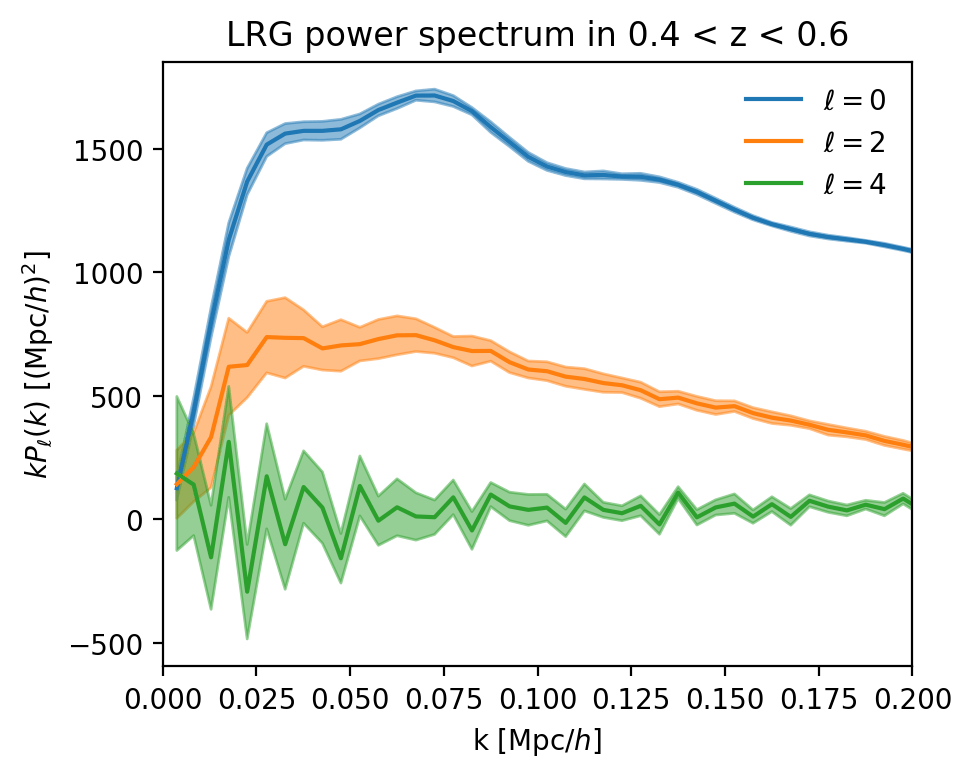
BAO detection: \(14.7\sigma\)
0.1 < z < 0.4
0.4 < z < 0.6
0.6 < z < 0.8
0.8 < z < 1.1
1.1 < z < 1.6
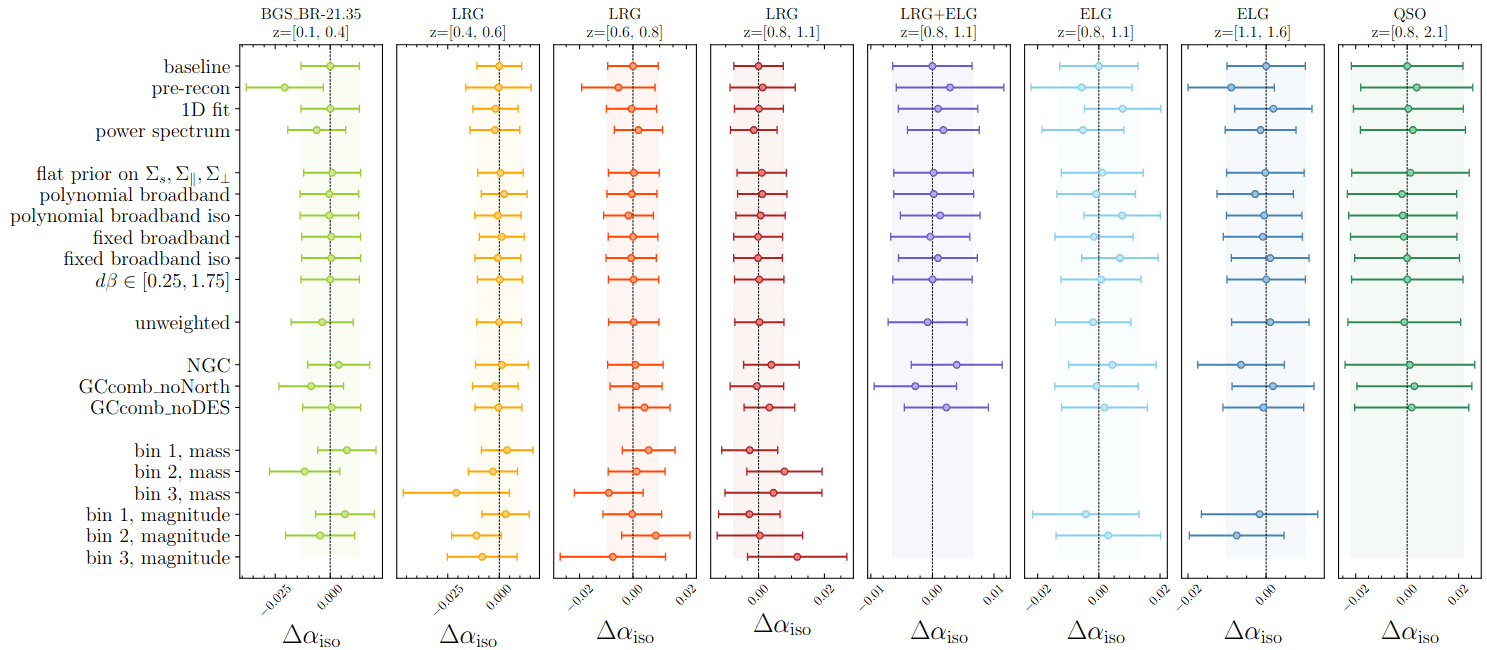
Robustness tests
tracers / redshift bins
data vector
Robustness tests
tracers / redshift bins
BAO modelling
Robustness tests
tracers / redshift bins
imaging systematics
Robustness tests
tracers / redshift bins
data splits
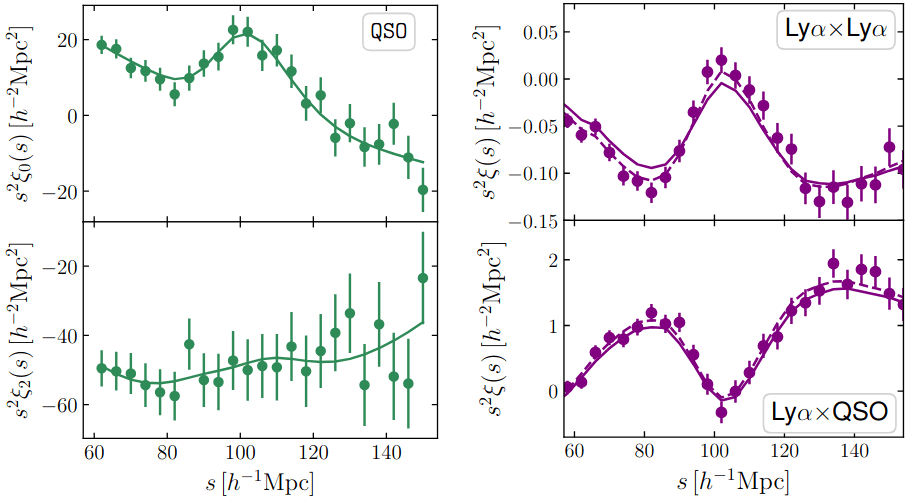
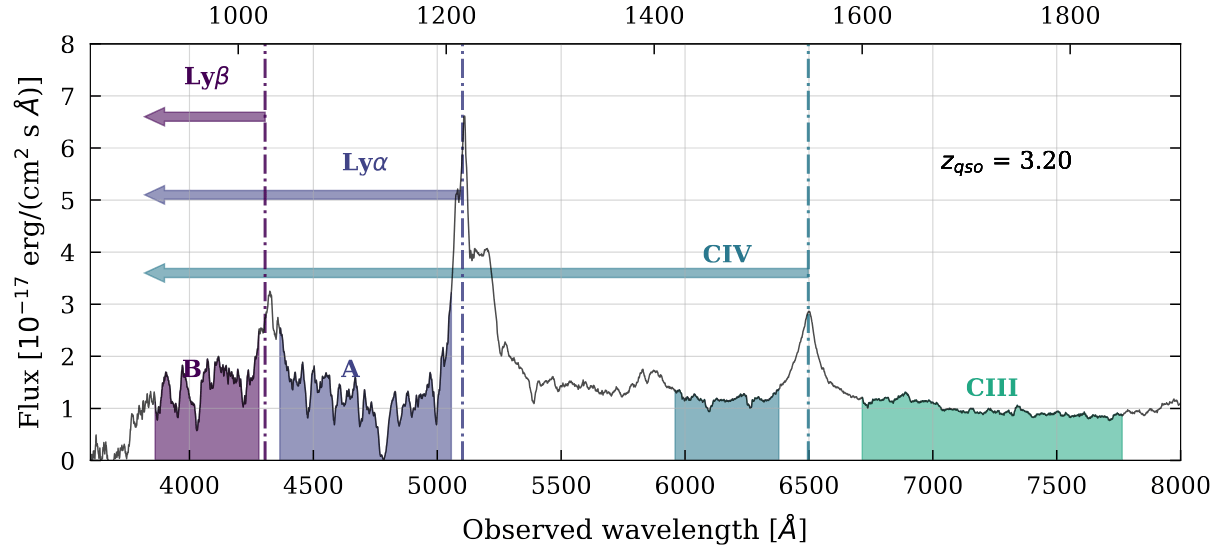
Ly\(\alpha\) forest
Ly\(\alpha\) forest
Absorption in QSO spectra by neutral hydrogen in the intergalactic medium: \(\lambda_\mathrm{abs} = (1 + z_\mathrm{HI}) \times 1215.17 \; \AA \)
Transmitted flux fraction \(F = e^{-\tau}\) probes the fluctuation in neutral hydrogen density, \(\tau \propto n_\mathrm{HI} \)
credit: Andrew Pontzen
Correlation functions
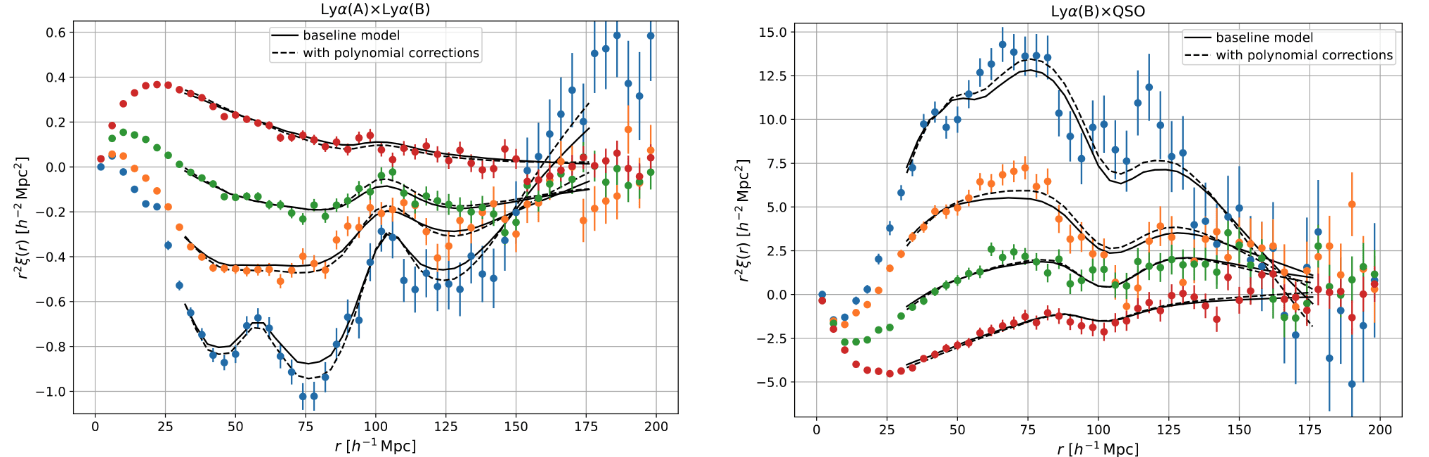
Ly\(\alpha\) forest auto-correlation
\(\langle \delta_F(\mathbf{x}) \delta_F(\mathbf{x + s}) \rangle\)
Ly\(\alpha\) forest - QSO cross-correlation
\(\langle \delta_F(\mathbf{x}) Q(\mathbf{x + s}) \rangle\)
Robustness tests
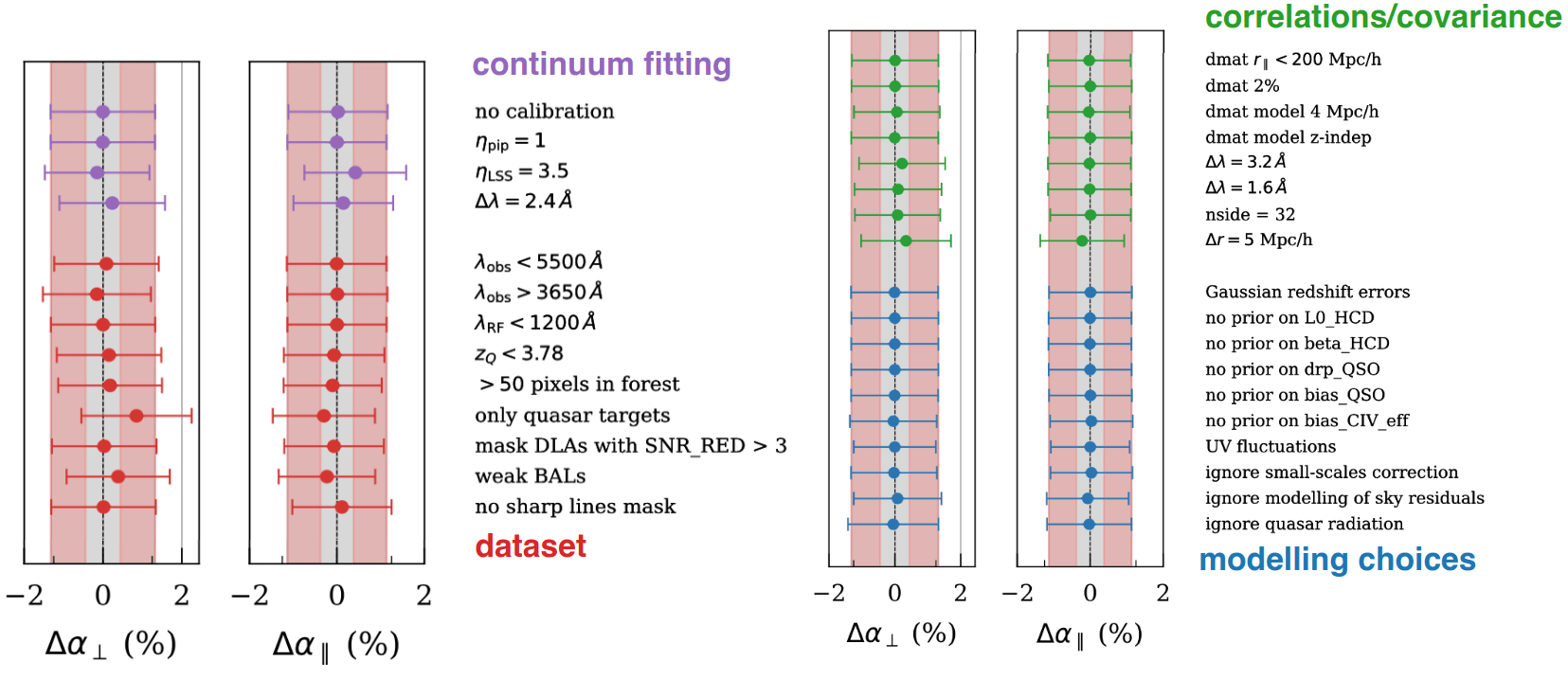
data vector / covariance
Robustness tests
modelling choices
Robustness tests
continuum fitting
Robustness tests
data splits
What's new in the analyses?
Analysis pipelines mostly the same as DR1
Again, blind analyses:
- discrete tracers: catalog-level blinding
- Ly\(\alpha\): data vector-level blinding
Subdominant systematics:
- discrete tracers: \(\sigma_\mathrm{stat+syst} < 1.09 \sigma_\mathrm{stat}\)
- Ly\(\alpha\): \(<1.06 \sigma_\mathrm{stat}\)
DESI DR2 BAO
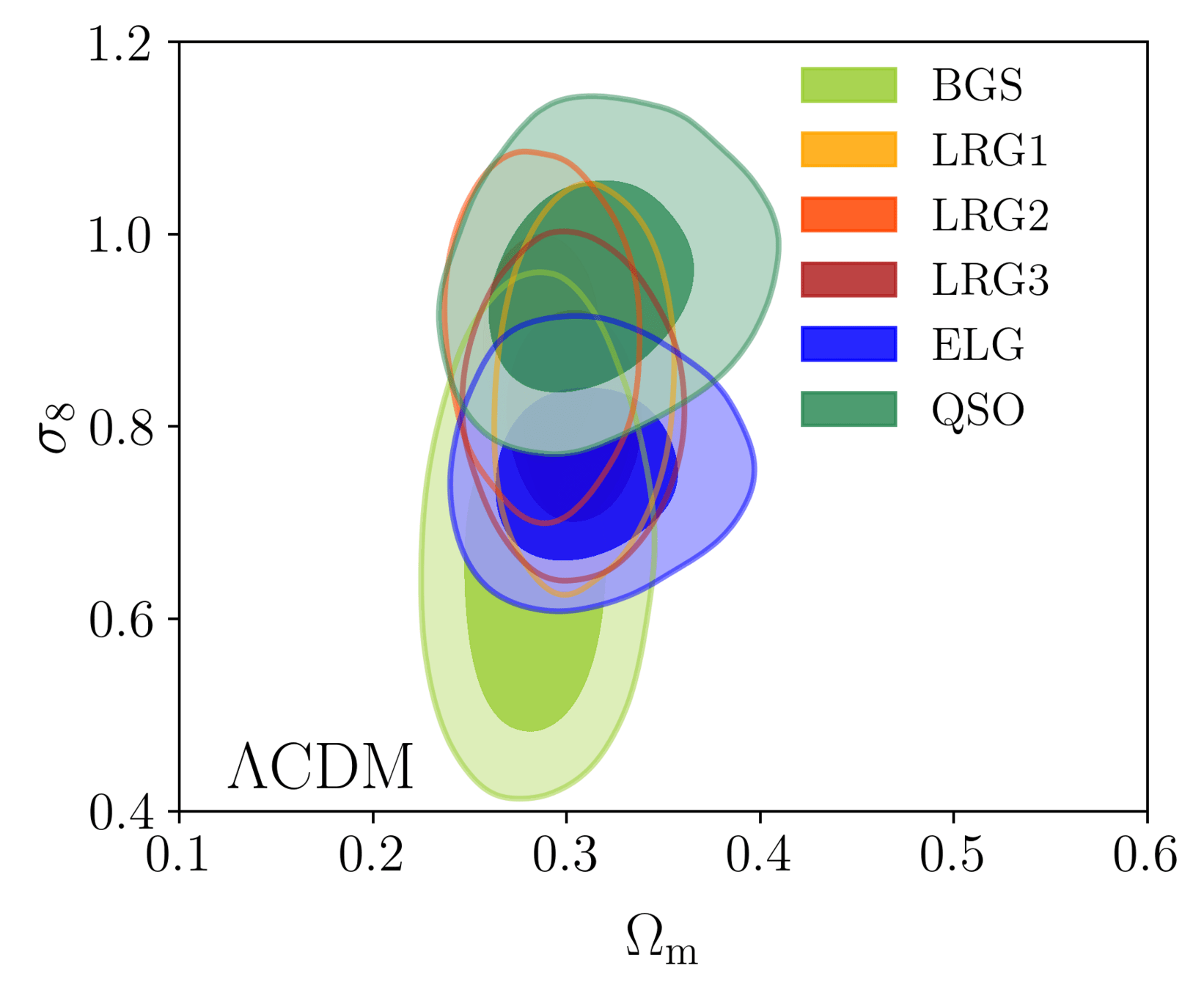
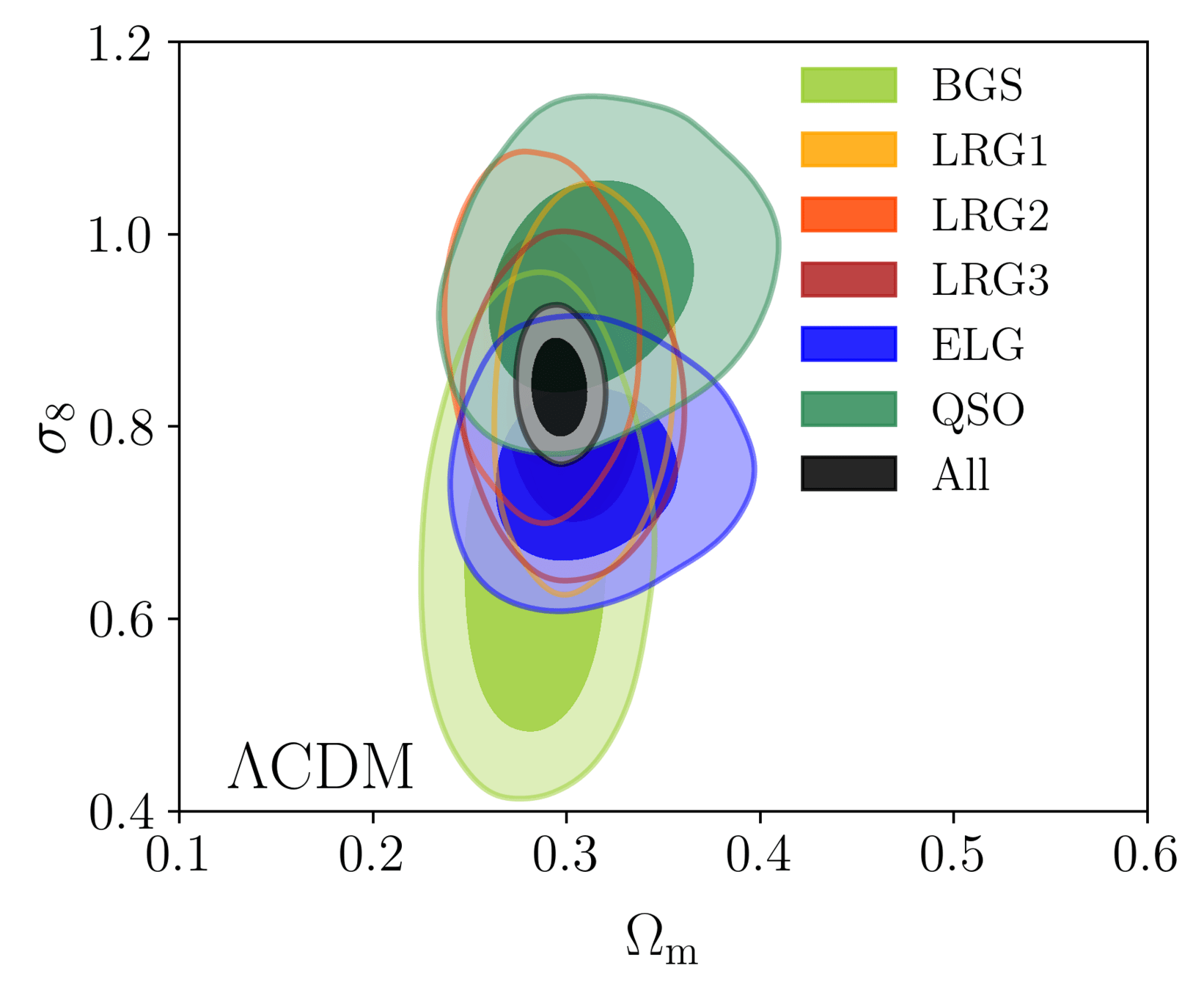
DESI DR2 BAO measurements
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
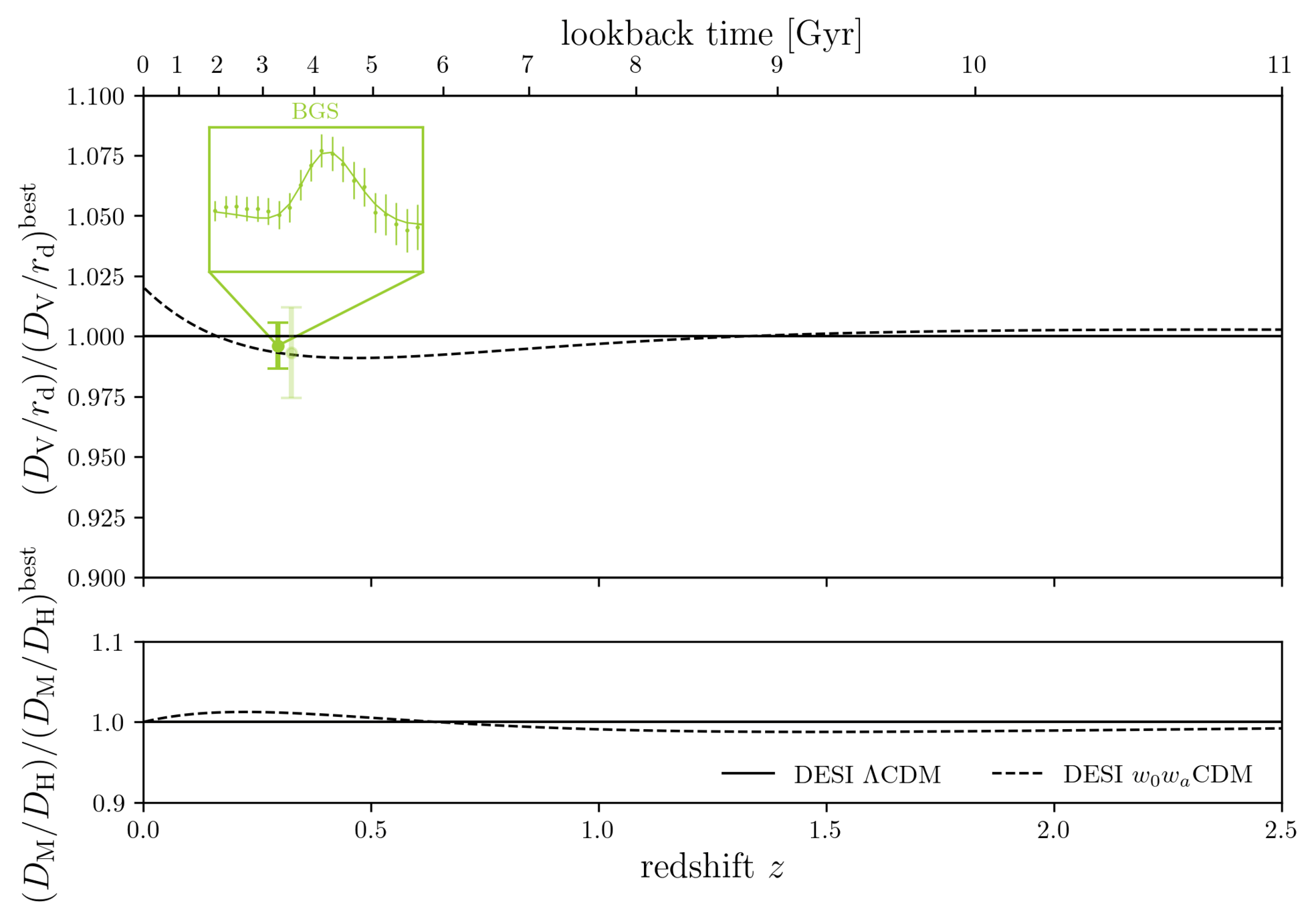
DESI DR2 BAO
DESI DR2 BAO measurements
\propto (D_{\mathrm{M}}(z) / D_\mathrm{H}(z)) = f(\Omega_\mathrm{m})
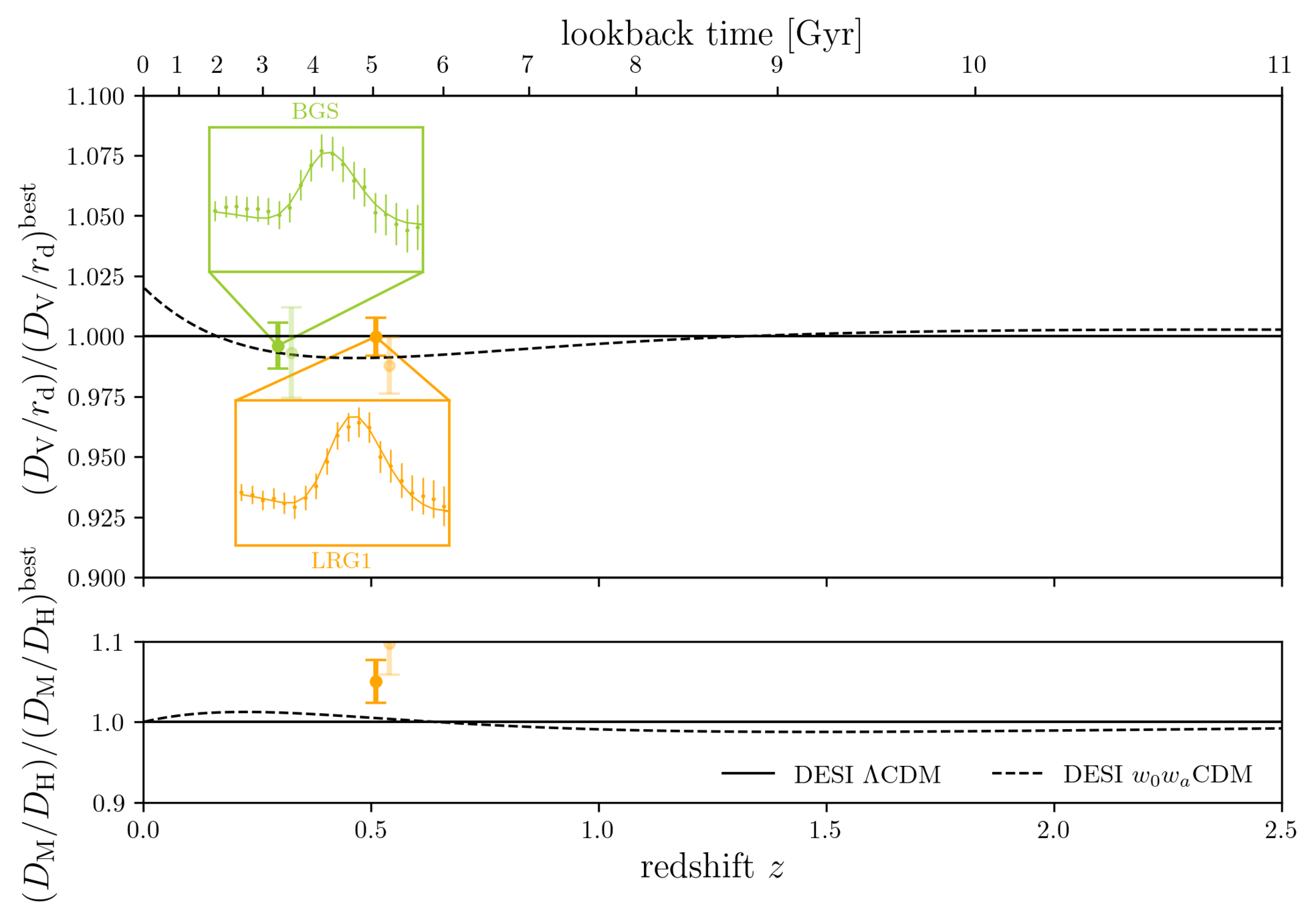
DESI DR2 BAO
DESI DR2 BAO measurements
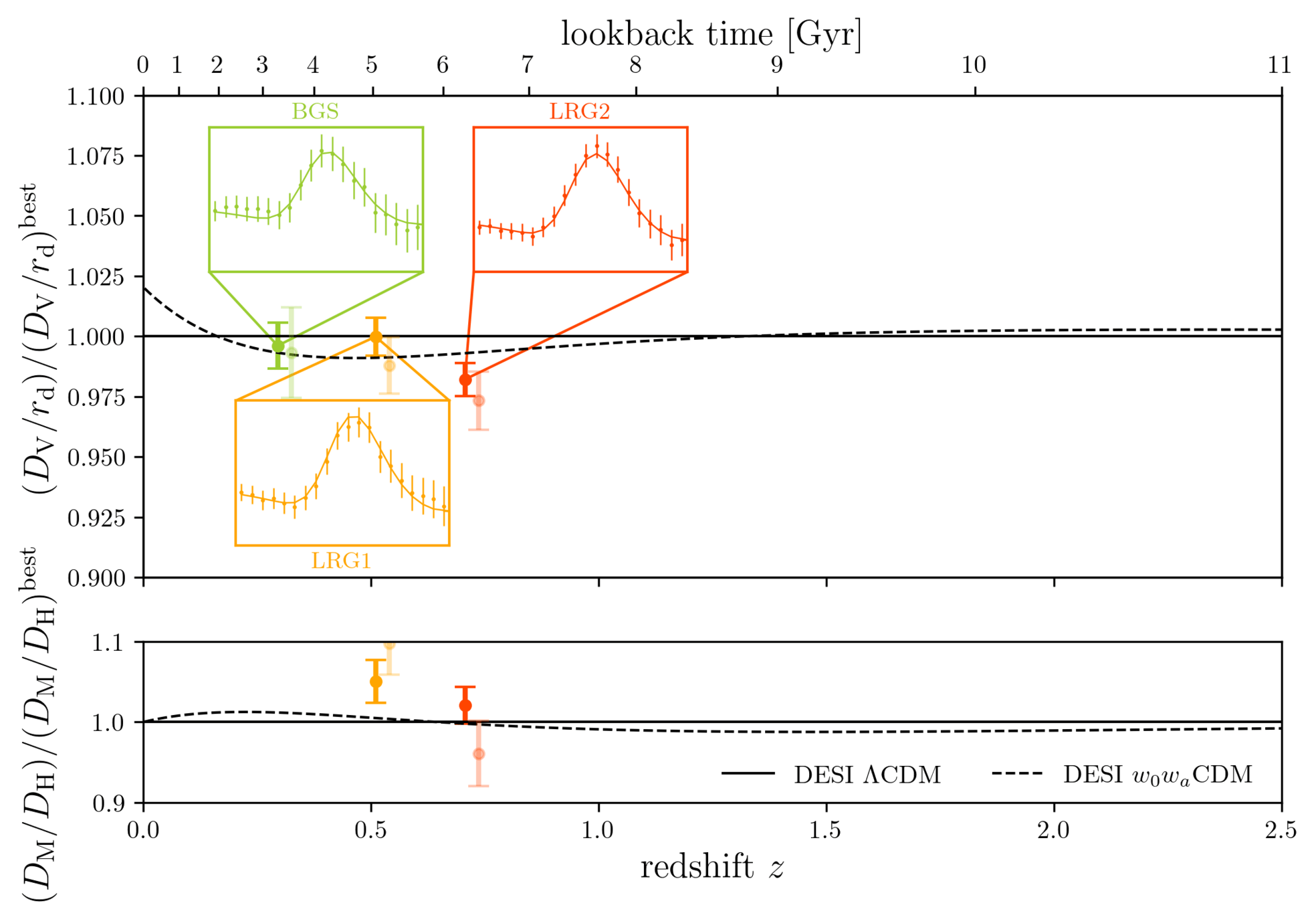
DESI DR2 BAO
DESI DR2 BAO measurements
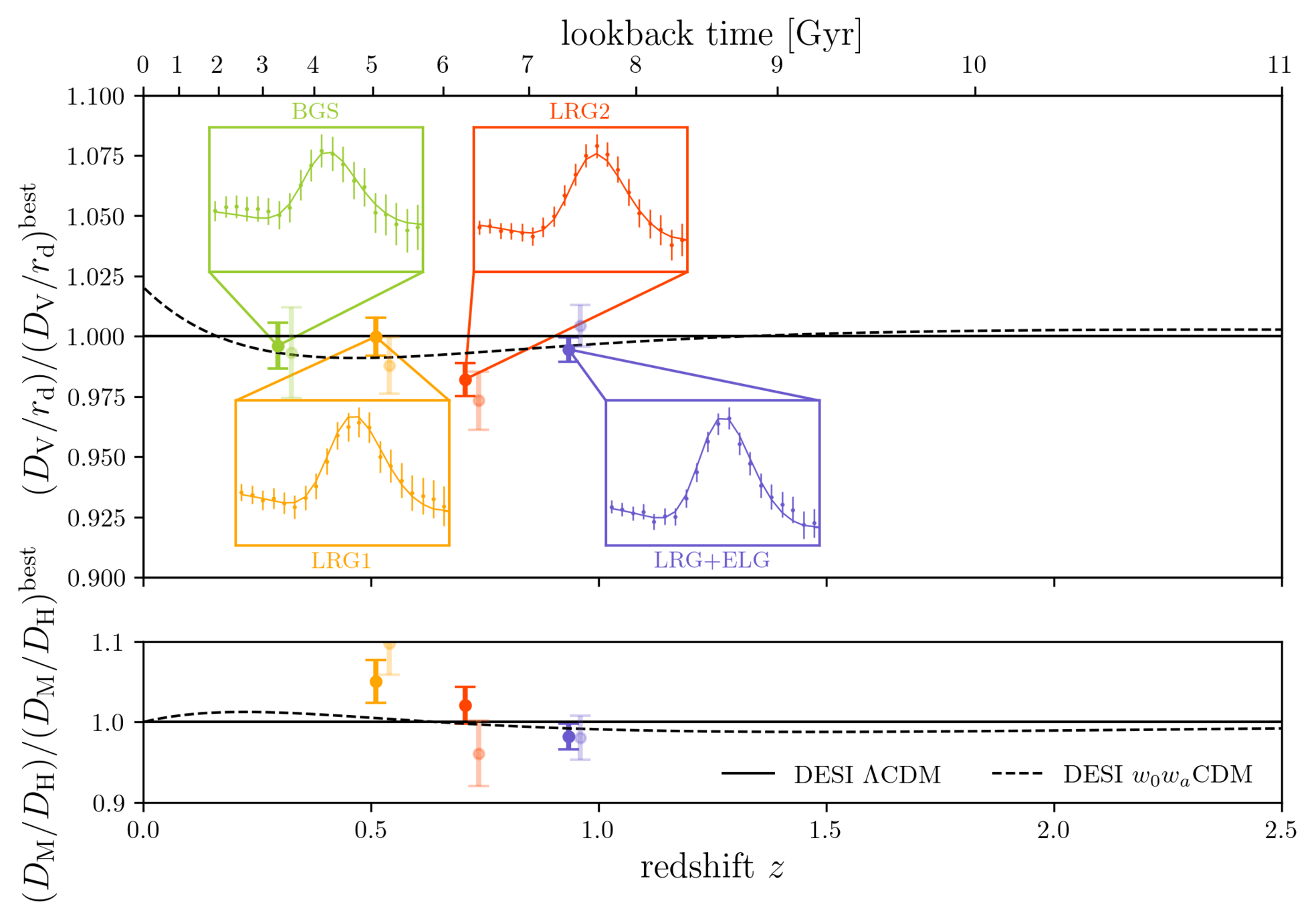
DESI DR2 BAO
DESI DR2 BAO measurements
DESI DR2 BAO
DESI DR2 BAO measurements
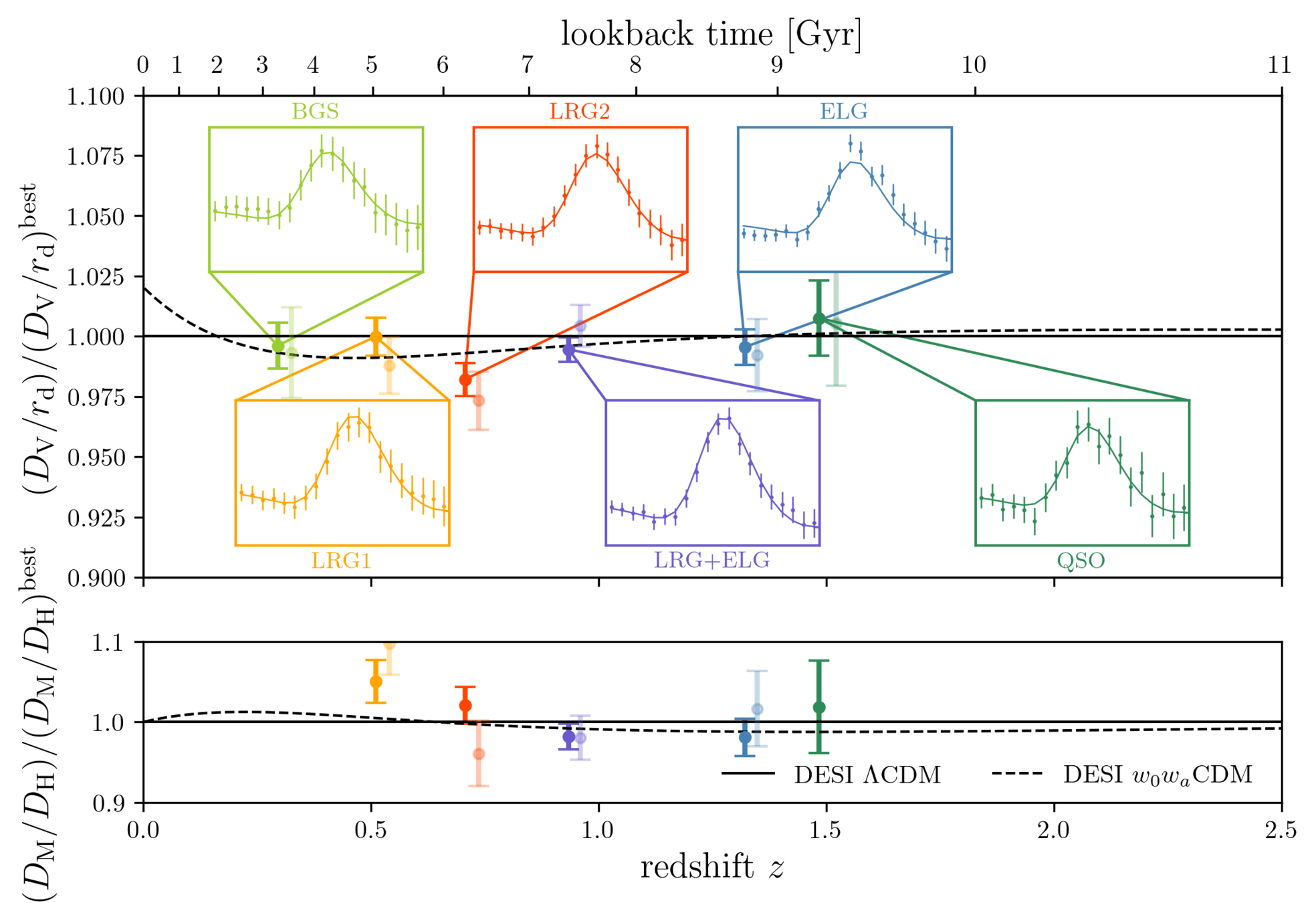
DESI DR2 BAO
DESI DR2 BAO measurements
Consistent with each other,
and complementary
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.2975 \pm 0.0086 & \mathbf{(3.0\%)} \\
H_{0} r_\mathrm{d} &= (101.54 \pm 0.73) \, [100 \, \mathrm{km} \, \mathrm{s}^{-1}] & \mathbf{(0.7\%)}
\end{align*}}_{\textstyle \text{\color{black}{DESI}}}
DESI DR2 BAO
DESI DR2 BAO measurements
- DESI DR2 BAO fully consistent with DESI DR1
- Improvement of \(\simeq 40\%\)
- \(2.3 \sigma\) discrepancy with primary CMB¹ + CMB lensing²
Consistency with other data
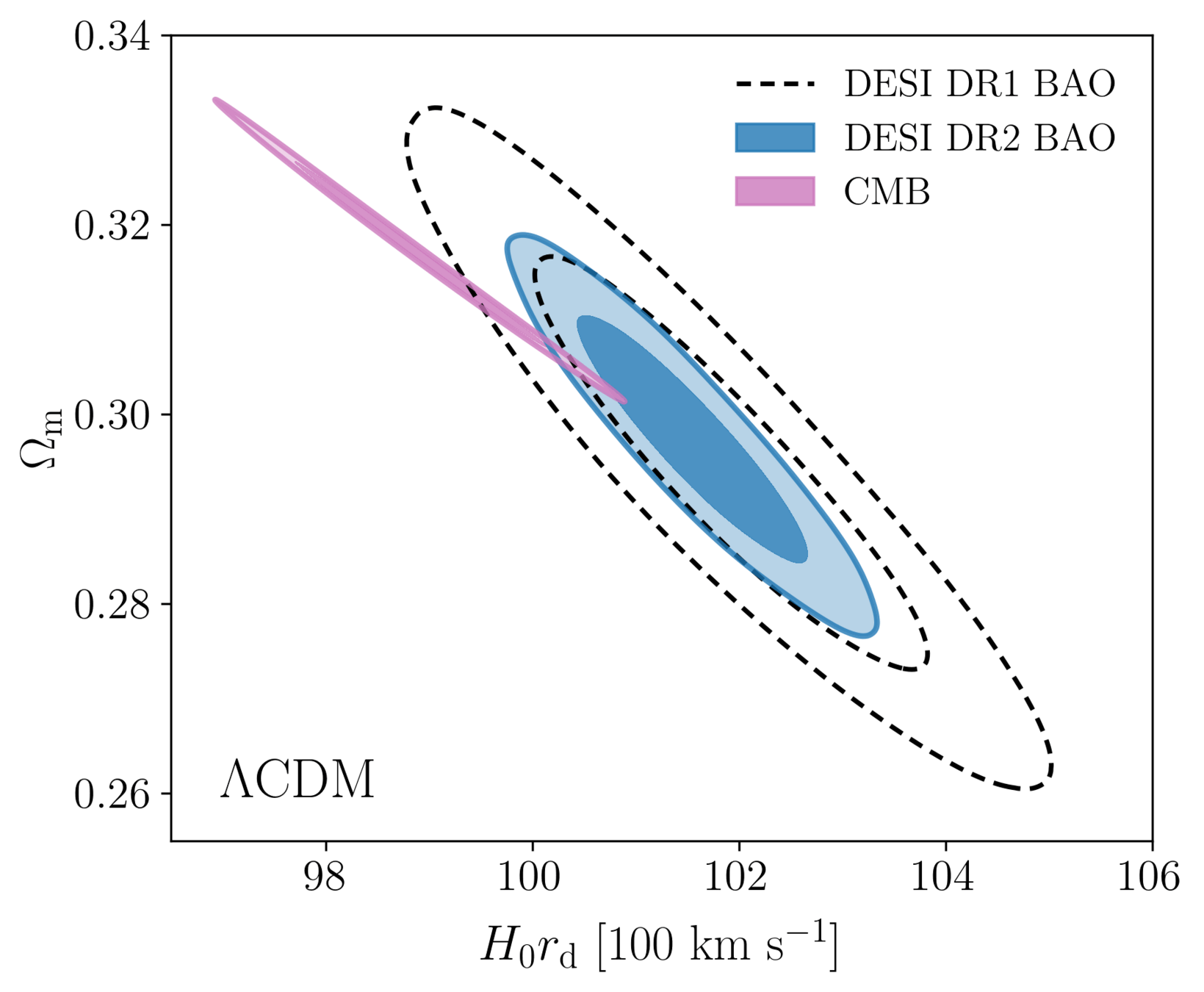
1. Planck PR4 CamSpec
2. Planck PR4 + ACT DR6 lensing
Various CMB likelihoods
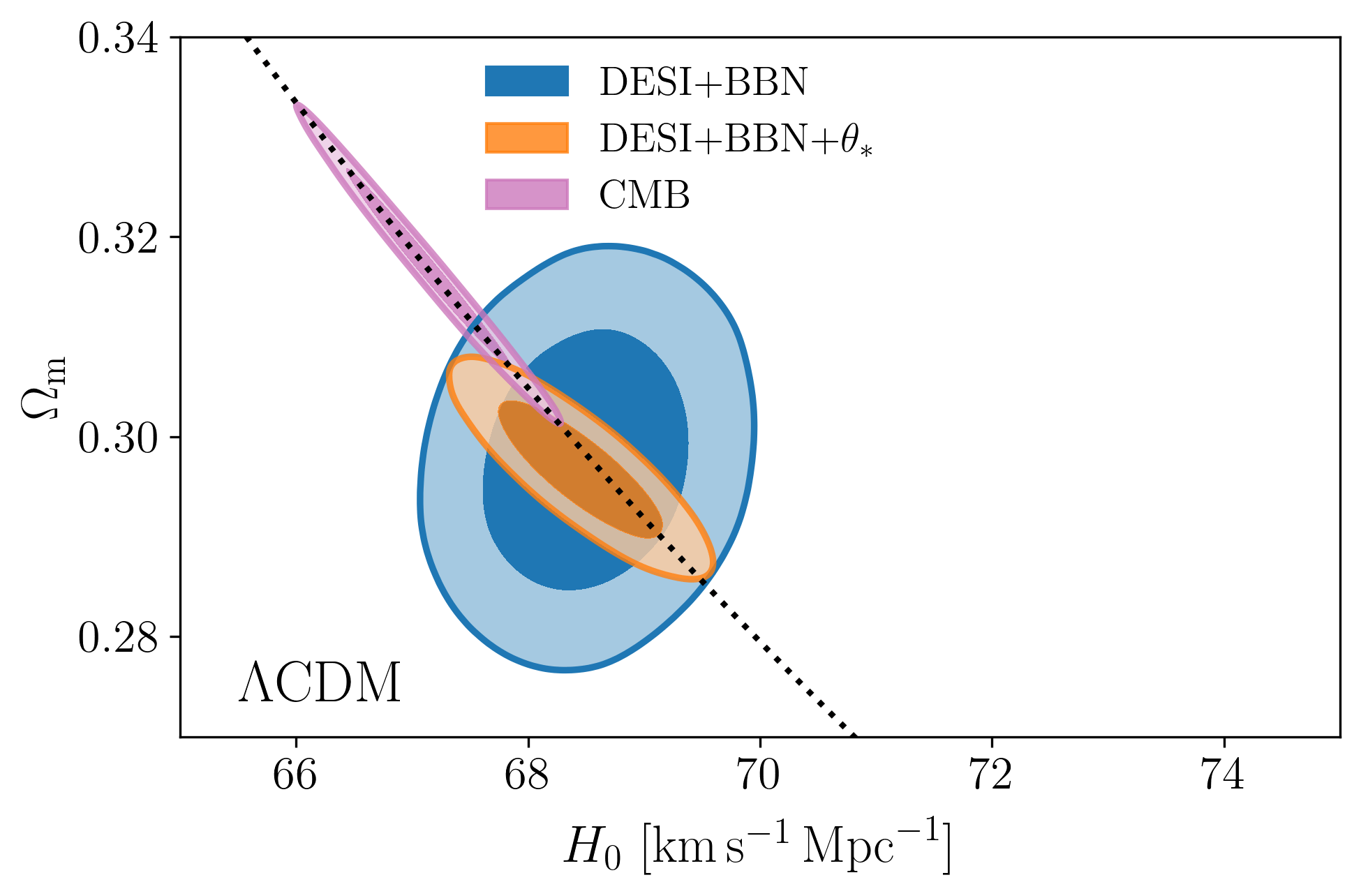
- BAO constrains \(\Omega_\mathrm{m}\), \(h \times r_\mathrm{d}(\Omega_\mathrm{b}h^2, \Omega_\mathrm{bc}h^2)\)
- Calibrating BAO relative distance measurements using BBN \(\Omega_\mathrm{b} h^2\)
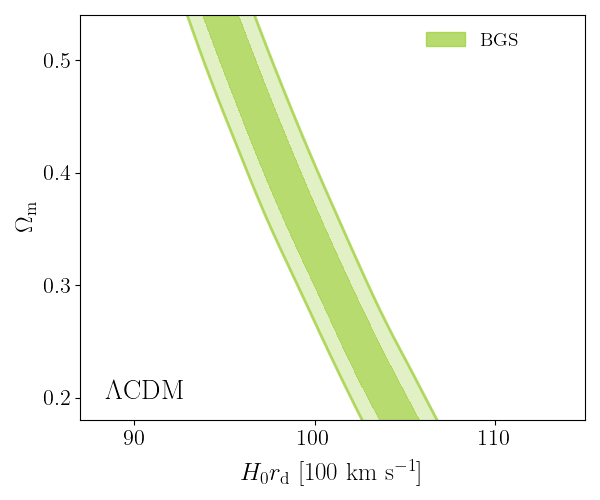
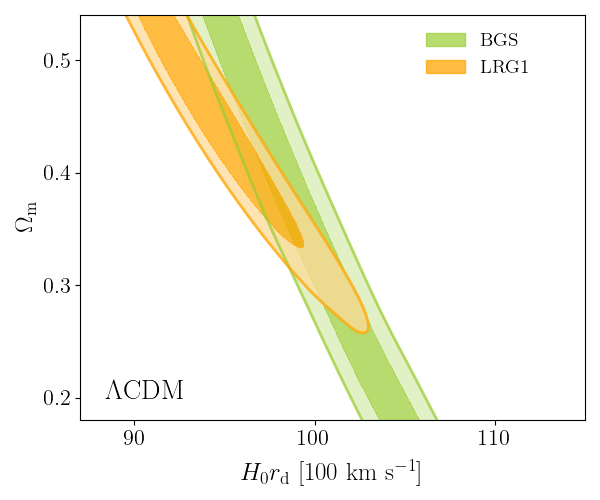
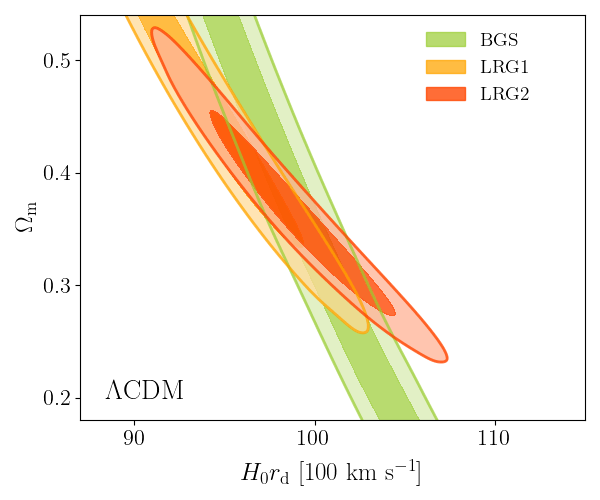
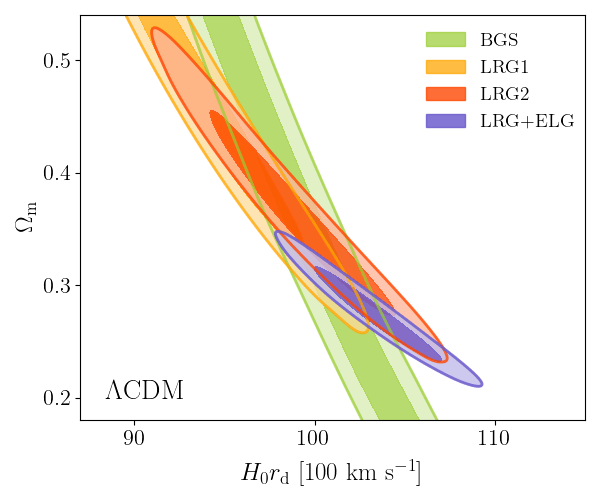
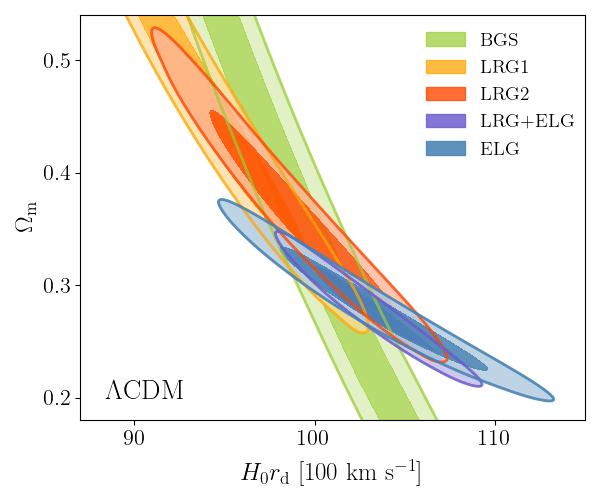
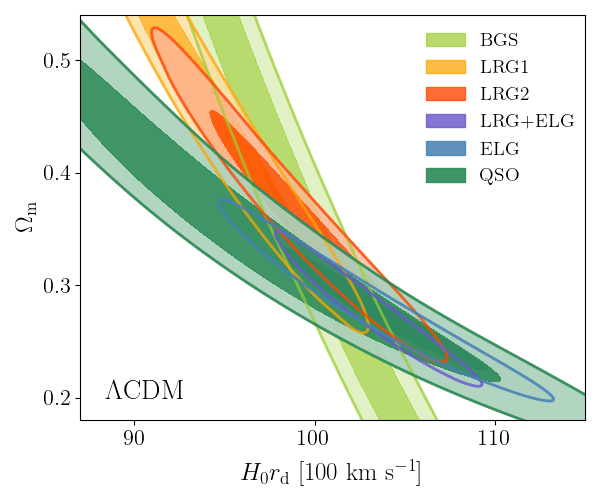
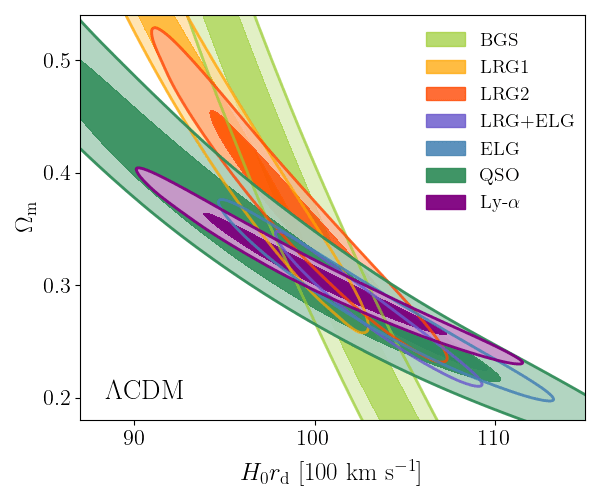
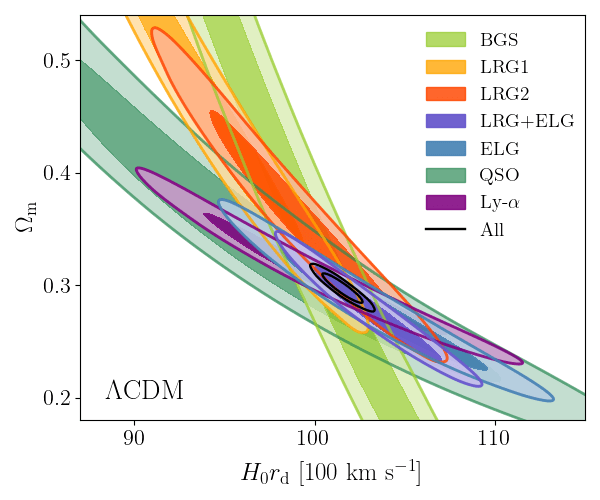
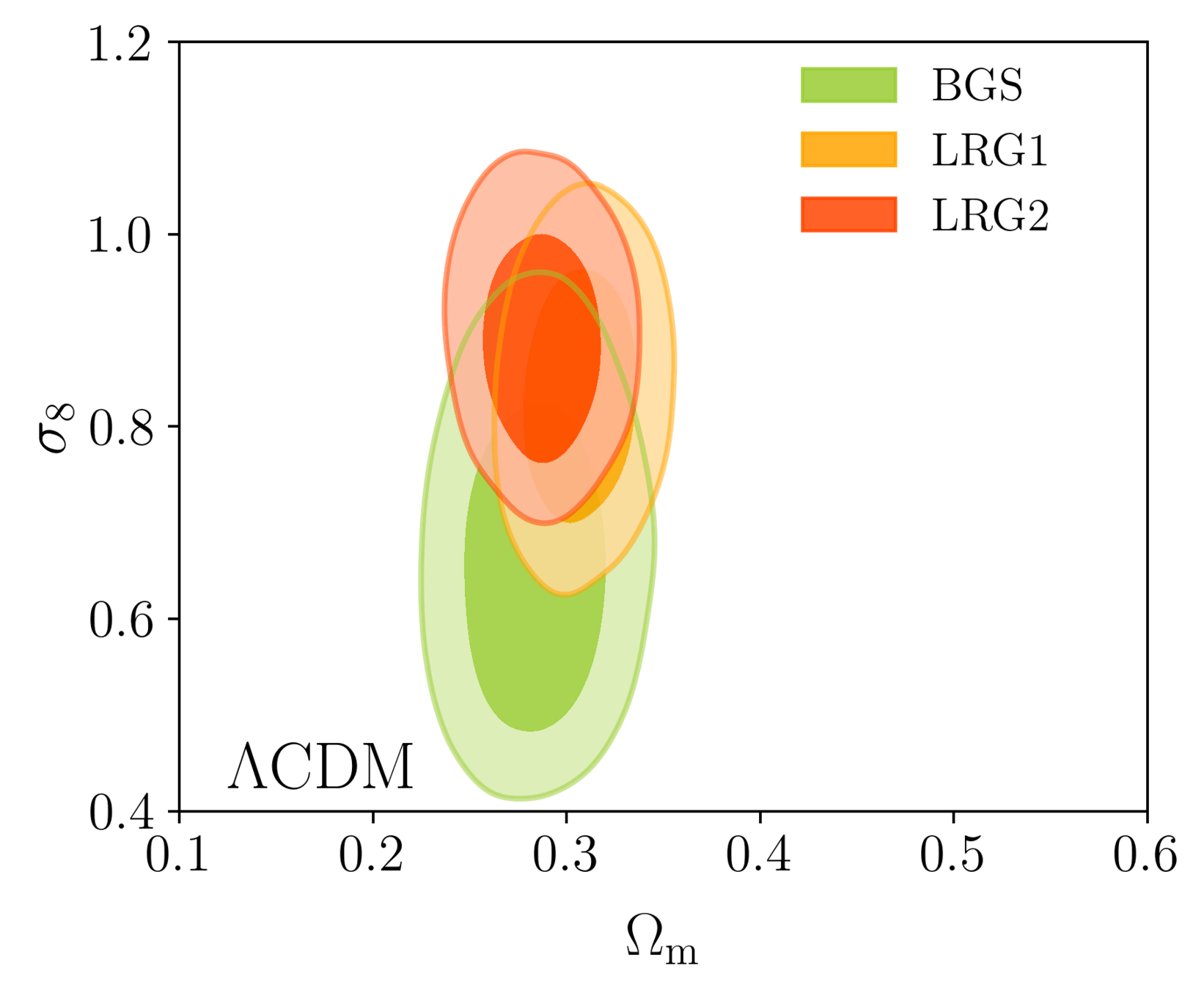
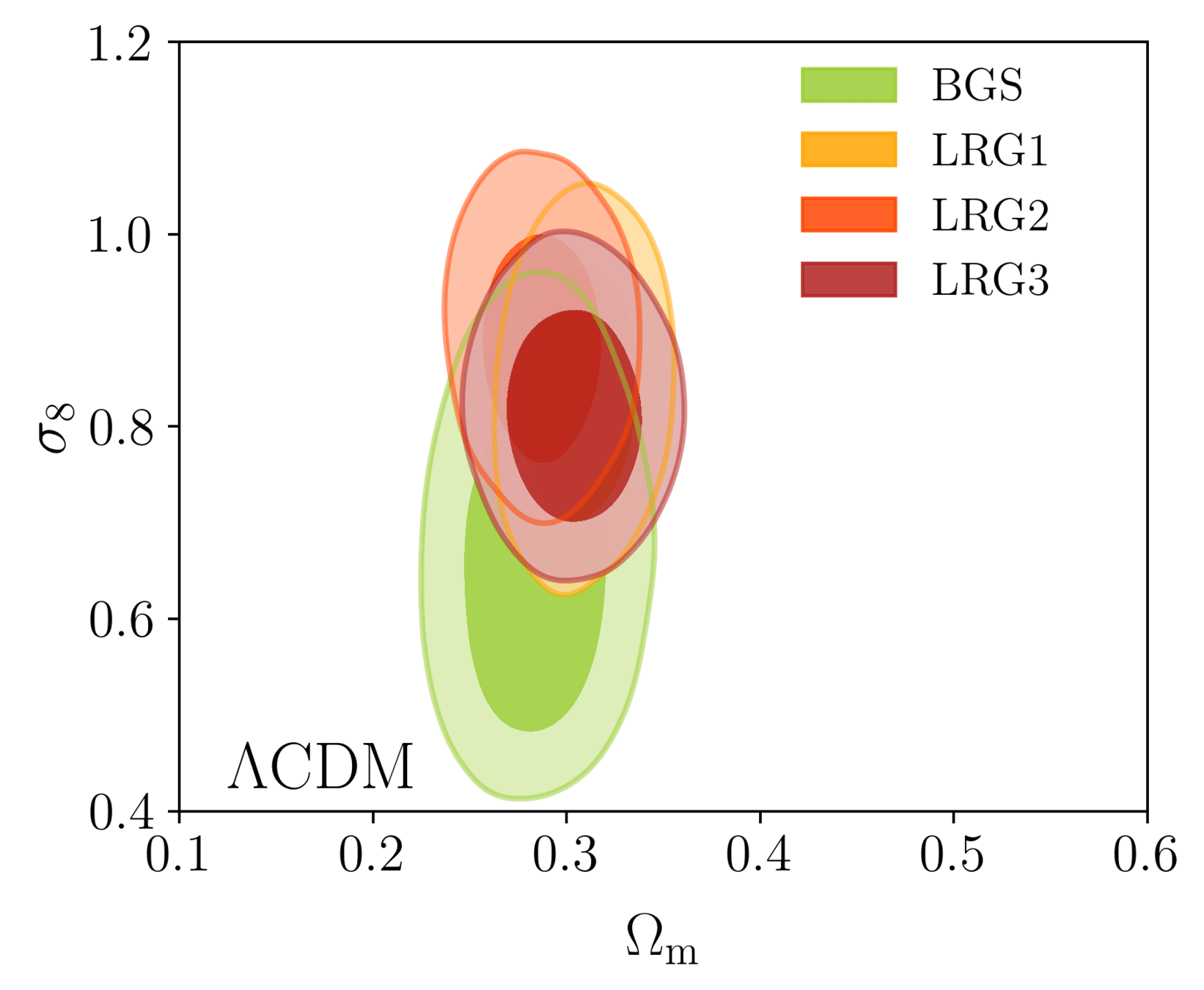
\(\Lambda\mathrm{CDM}\) constraints
\underbrace{
H_0 = (68.51 \pm 0.58) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
\(\Lambda\mathrm{CDM}\) constraints
\underbrace{
H_0 = (68.45 \pm 0.47) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{orange}{\text{DESI} + \theta_\ast + \text{BBN}}}
- BAO constrains \(\Omega_\mathrm{m}\), \(h \times r_\mathrm{d}(\Omega_\mathrm{b}h^2, \Omega_\mathrm{bc}h^2)\)
- Calibrating BAO relative distance measurements using BBN \(\Omega_\mathrm{b} h^2\)
\underbrace{
H_0 = (68.51 \pm 0.58) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
- Adding very precise CMB acoustic angular scale
\(\sim \Omega_\mathrm{m} h^3\)
\(\sim \Omega_\mathrm{m} h^2\)
\(\Lambda\mathrm{CDM}\) constraints
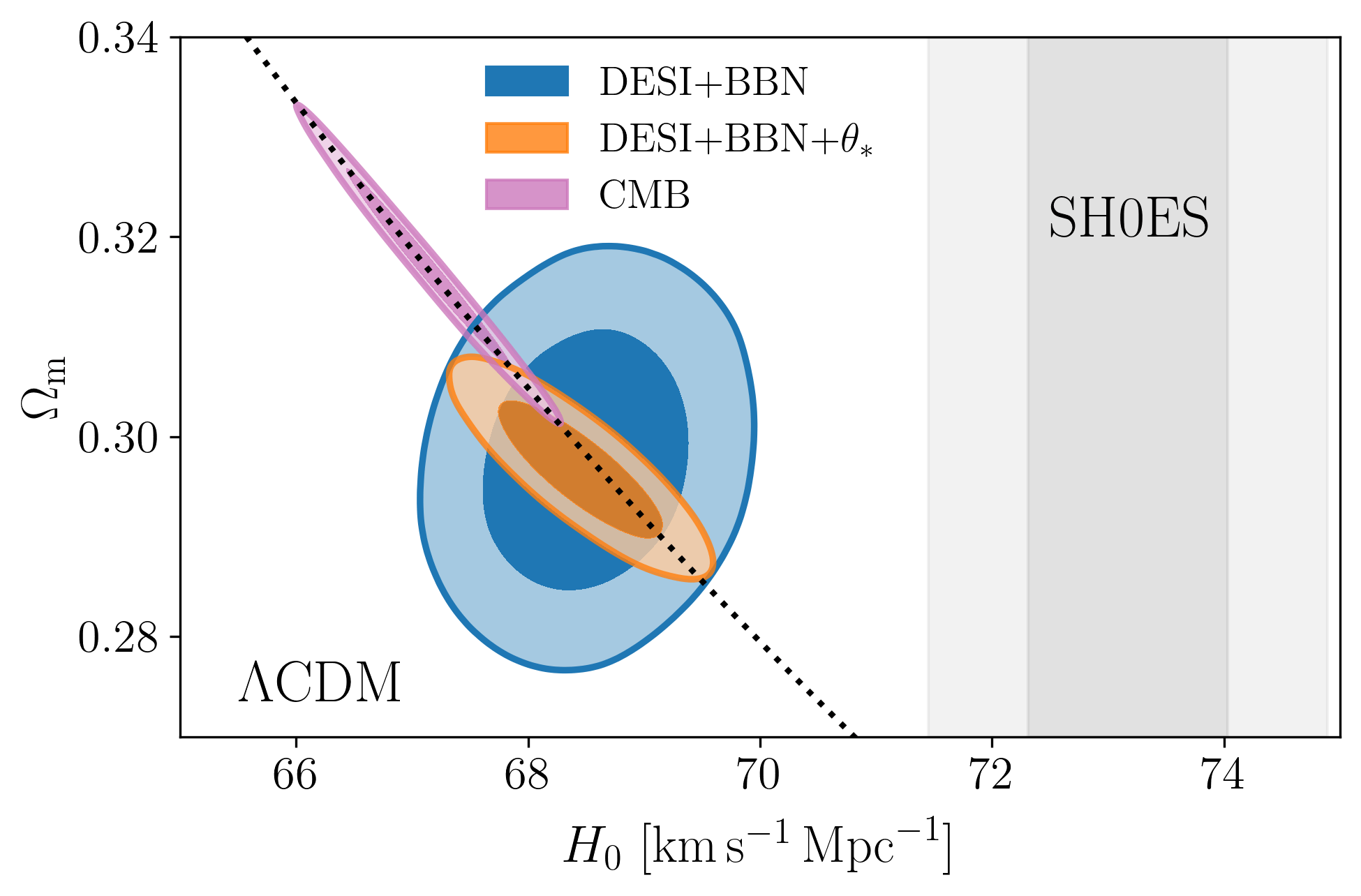
- In \(4.5\sigma\) tension with SH0ES (Breuval+24) (independently of the CMB)
- BAO constrains \(\Omega_\mathrm{m}\), \(h \times r_d(\Omega_\mathrm{b}h^2, \Omega_\mathrm{bc}h^2)\)
- Calibrating BAO relative distance measurements using BBN \(\Omega_\mathrm{b} h^2\)
\underbrace{
H_0 = (68.51 \pm 0.58) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
- Dark energy fluid
- No strong preference for dark energy evolution: \(1.7\sigma\) from DESI data alone
Dark Energy Equation of State
\(\Lambda\)
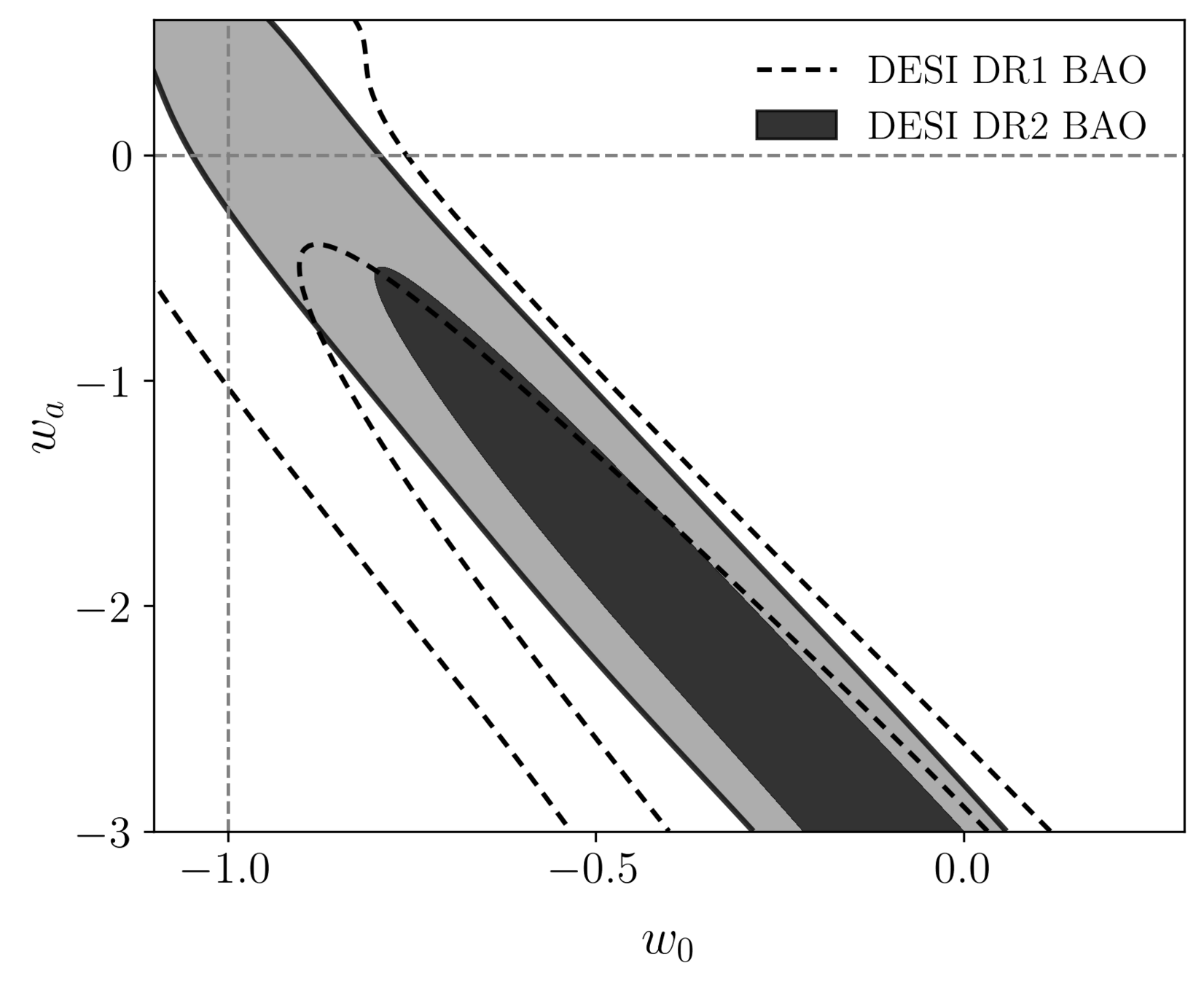
p / \rho = w = w_0 + w_a (1 - a)
pressure
density
CPL
- Combining DESI + CMB:
Dark Energy Equation of State
\underbrace{
w_{0} = -0.42 \pm 0.21 \qquad w_{a} = -1.75 \pm 0.58
}_{\textstyle \textcolor{orange}{\text{DESI + CMB} \; \implies \; 3.1\sigma}}
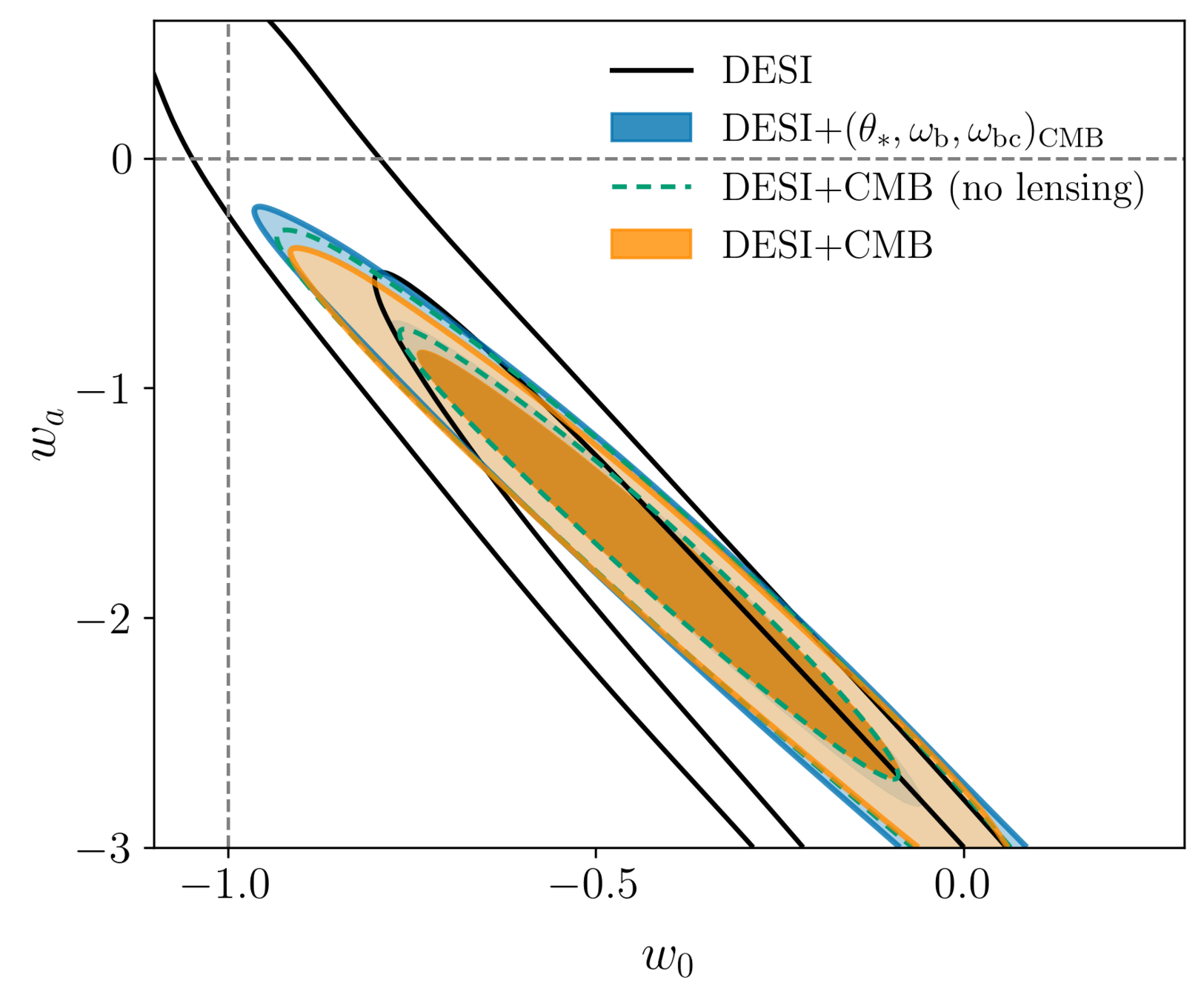
- CMB early-Universe priors: \(2.4\sigma\)
- Without CMB lensing \(2.7\sigma\)
\(+0.5\sigma\) compared to DR1
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.838 \pm 0.055 \qquad w_{a} = -0.62^{+0.22}_{-0.19}
}_{\textstyle \textcolor{blue}{\text{DESI + CMB + Pantheon+} \; \implies \; 2.8\sigma}}
\underbrace{
w_{0} = -0.667 \pm 0.088 \qquad w_{a} = -1.09^{+0.31}_{-0.27}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.8\sigma}}
\underbrace{
w_{0} = -0.752 \pm 0.057 \qquad w_{a} = -0.86^{+0.23}_{-0.20}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 4.2\sigma}}
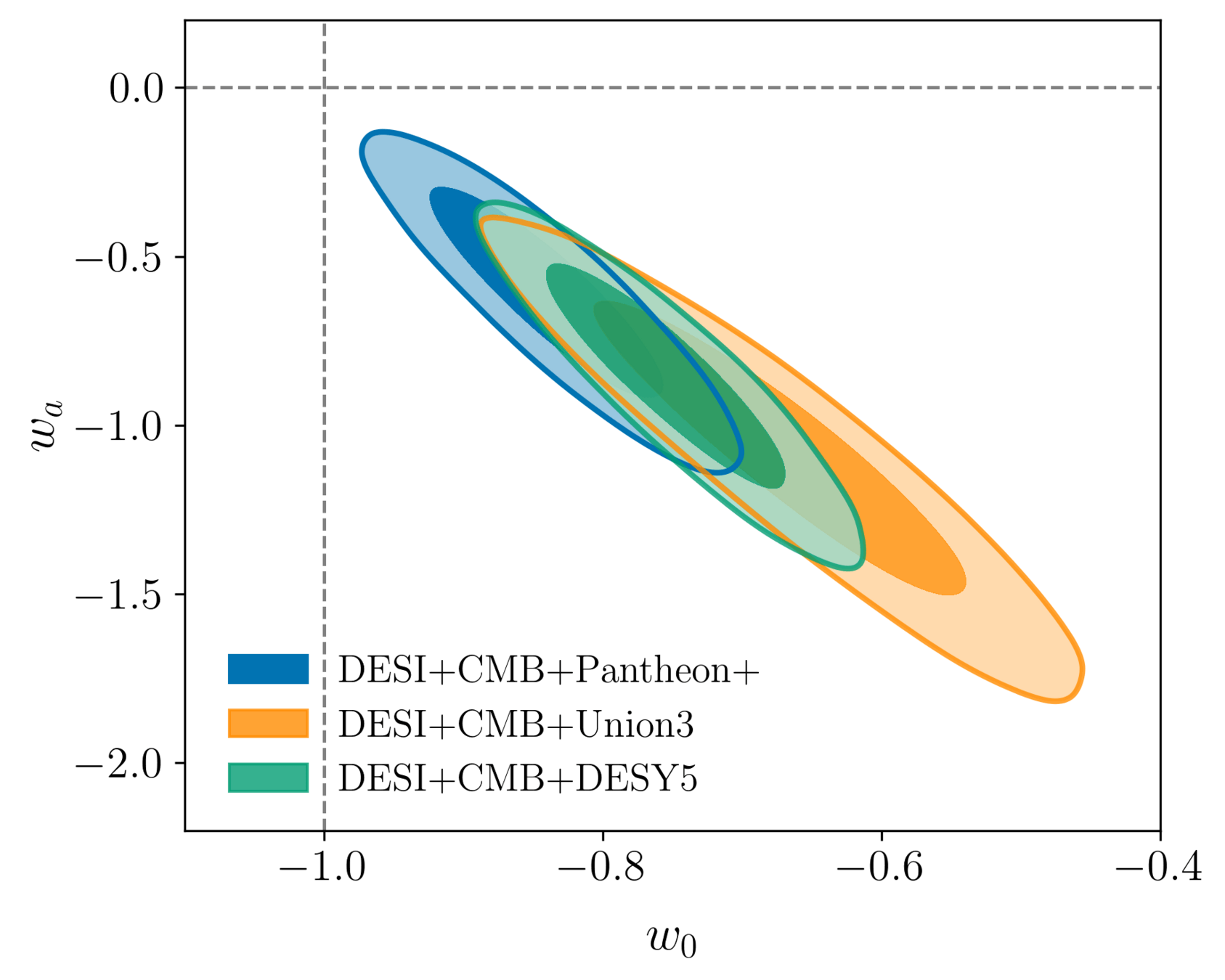
\(+0.3\sigma\) compared to DR1
Robustness tests
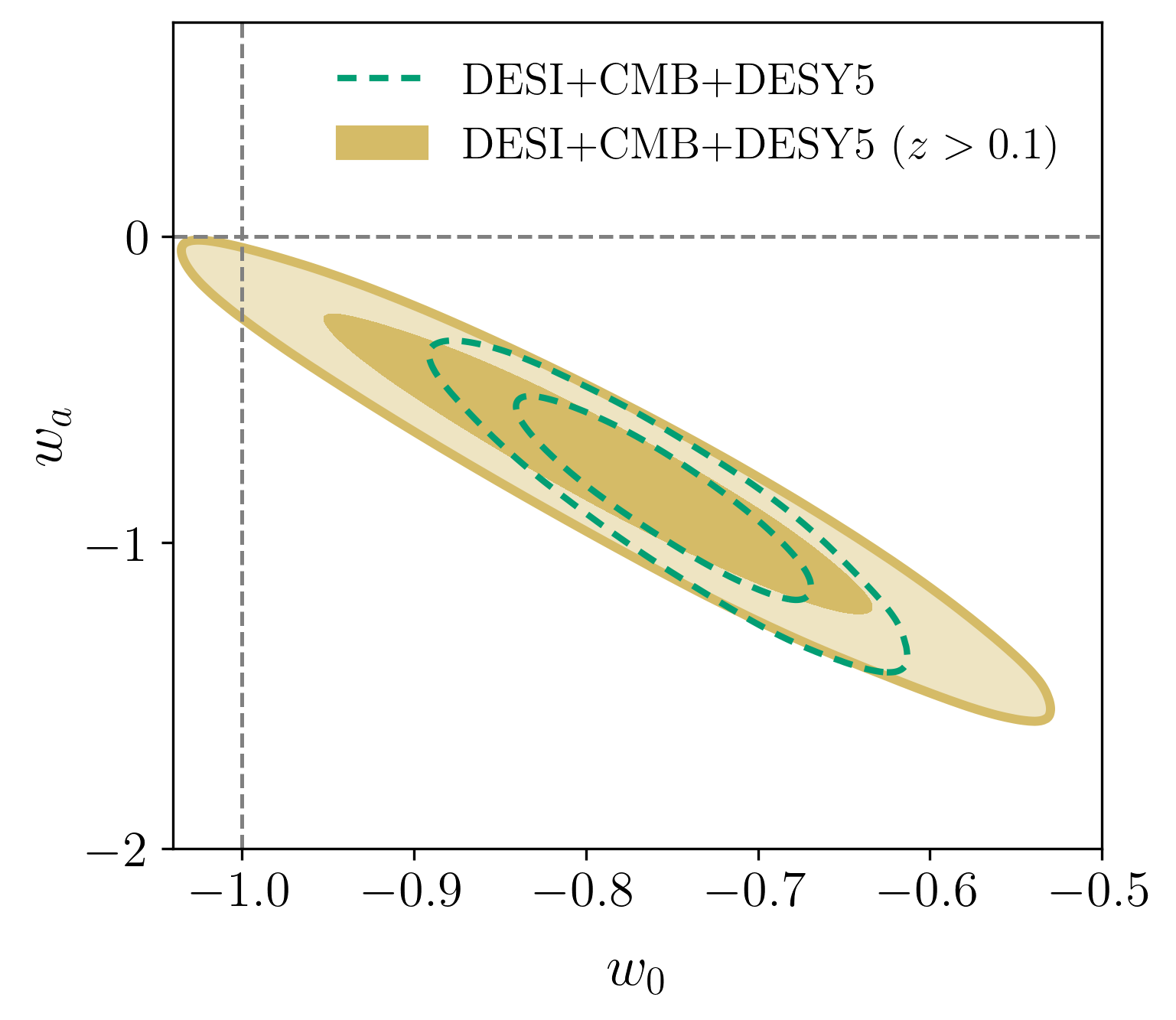
Removing low-\(z\) SN
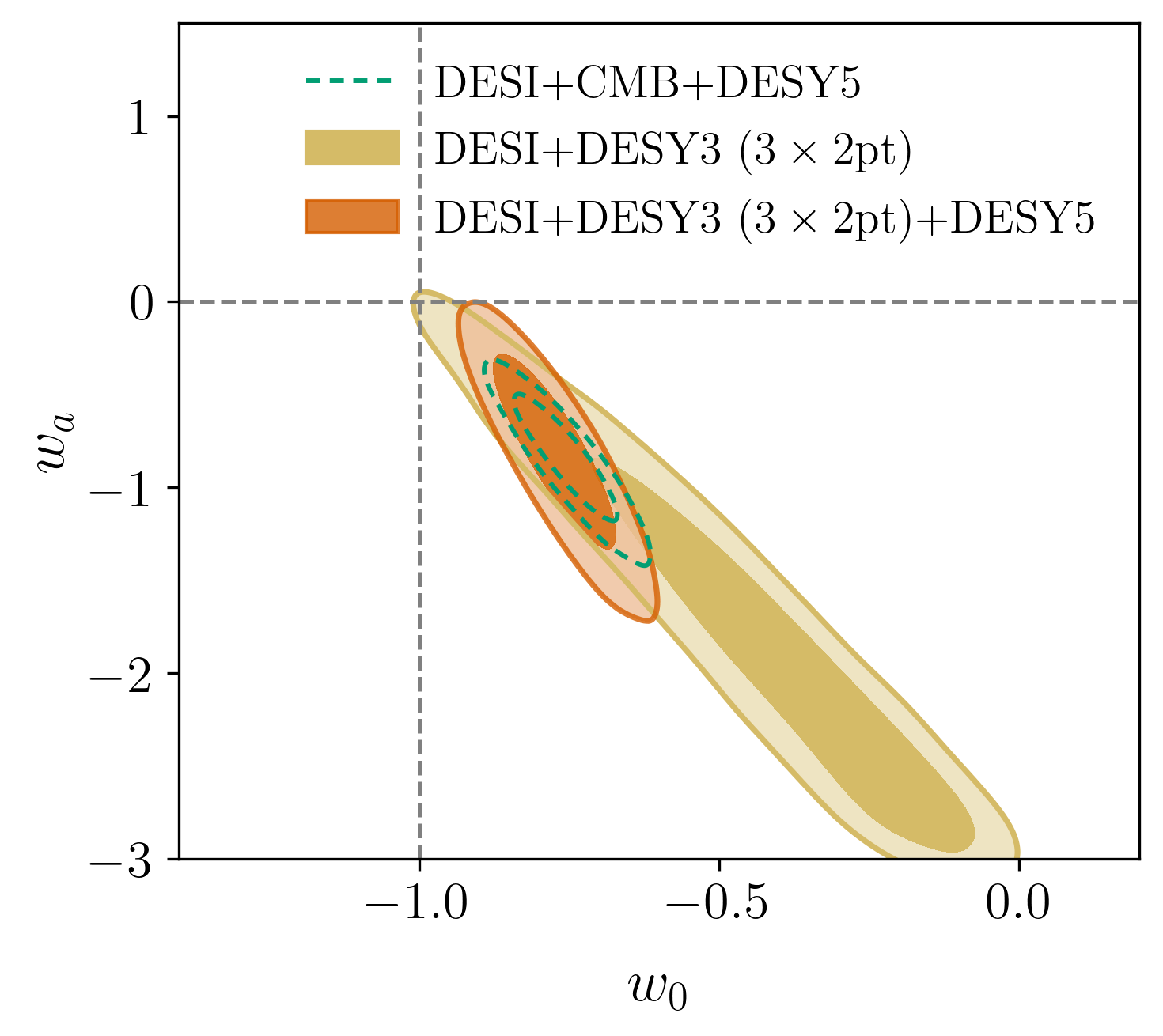
"Replacing CMB": DESY3 \(3\times2\)pt
\(3.3\sigma\)
Understanding tensions
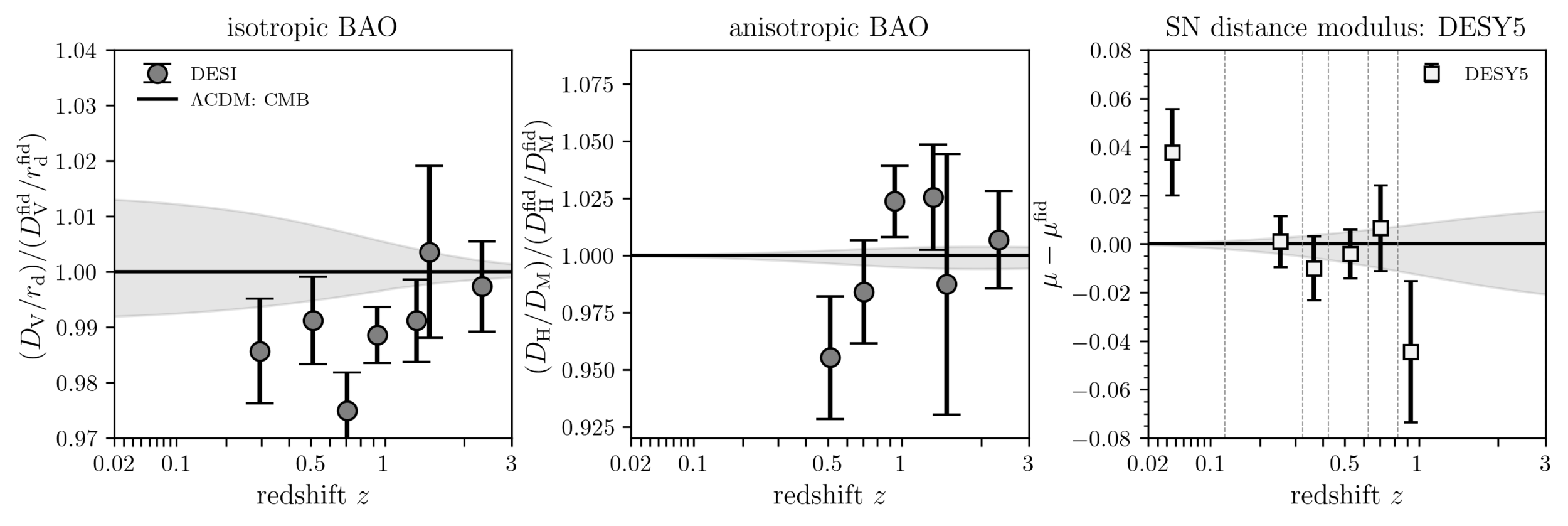
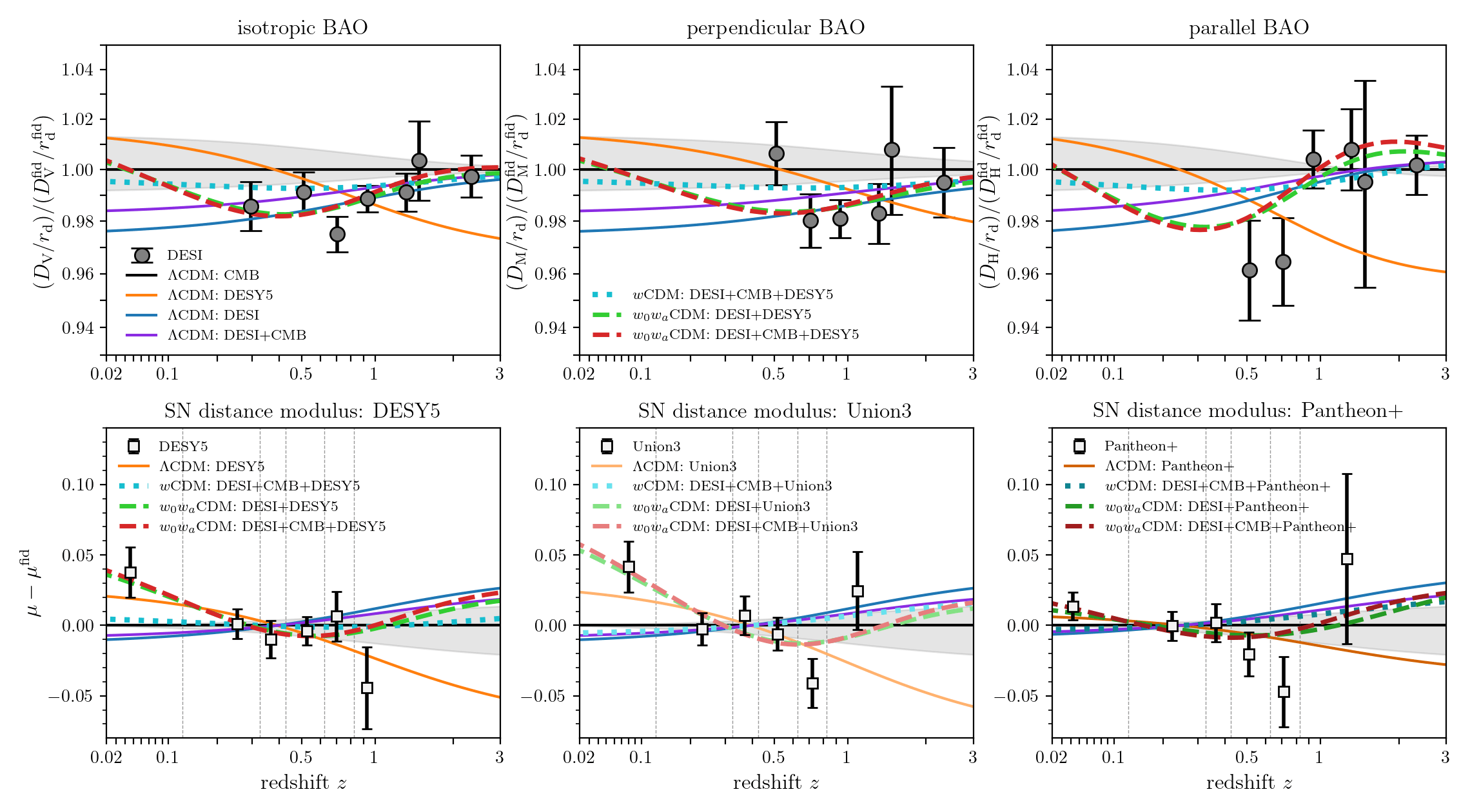
Understanding tensions
doesn't fit the SN!
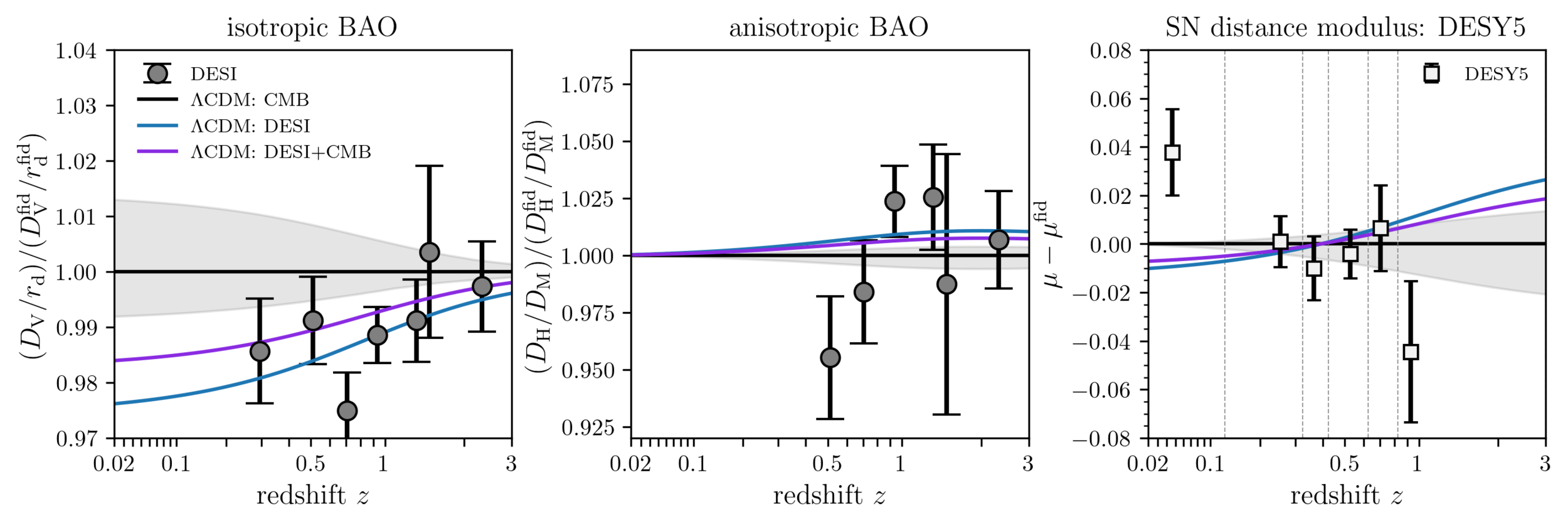
Understanding tensions
doesn't fit the BAO!
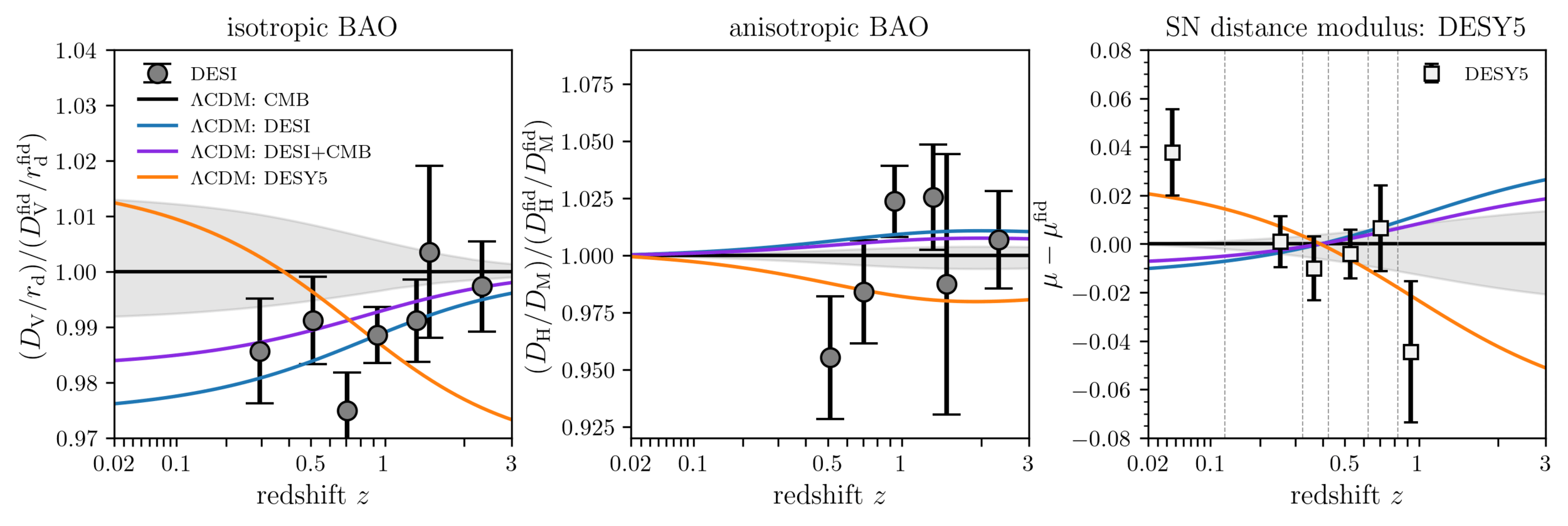
Understanding tensions
\(w\mathrm{CDM}\) not flexible enough to fit all 3 datasets!
w = -0.970
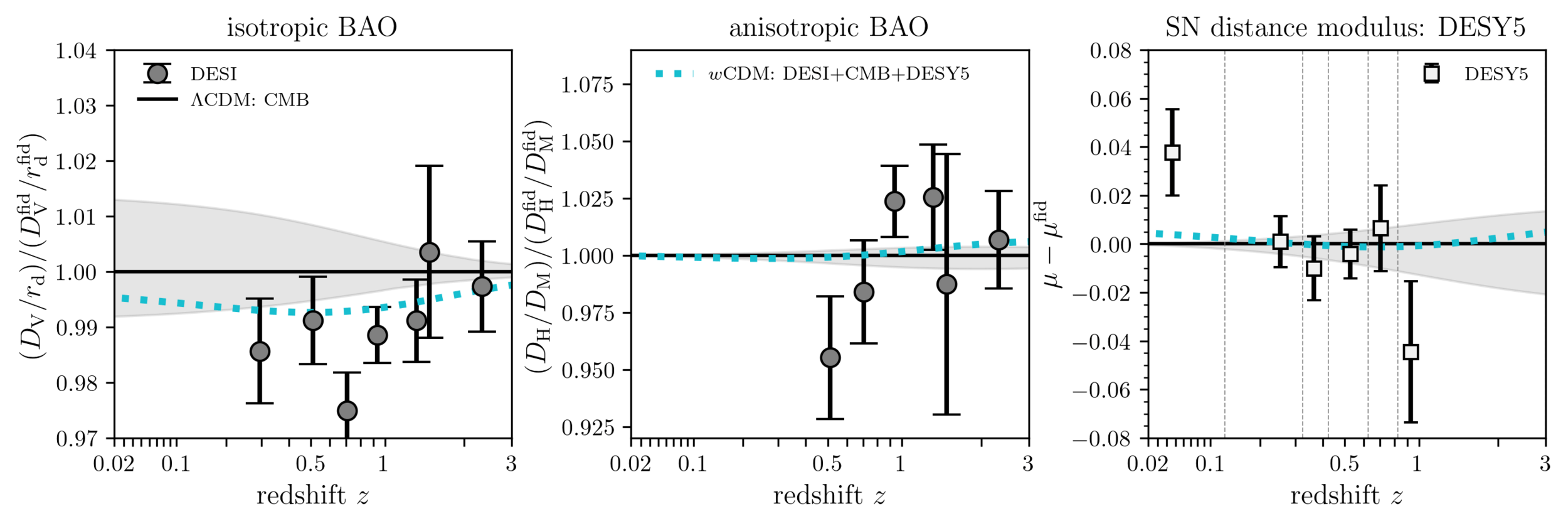
Understanding tensions
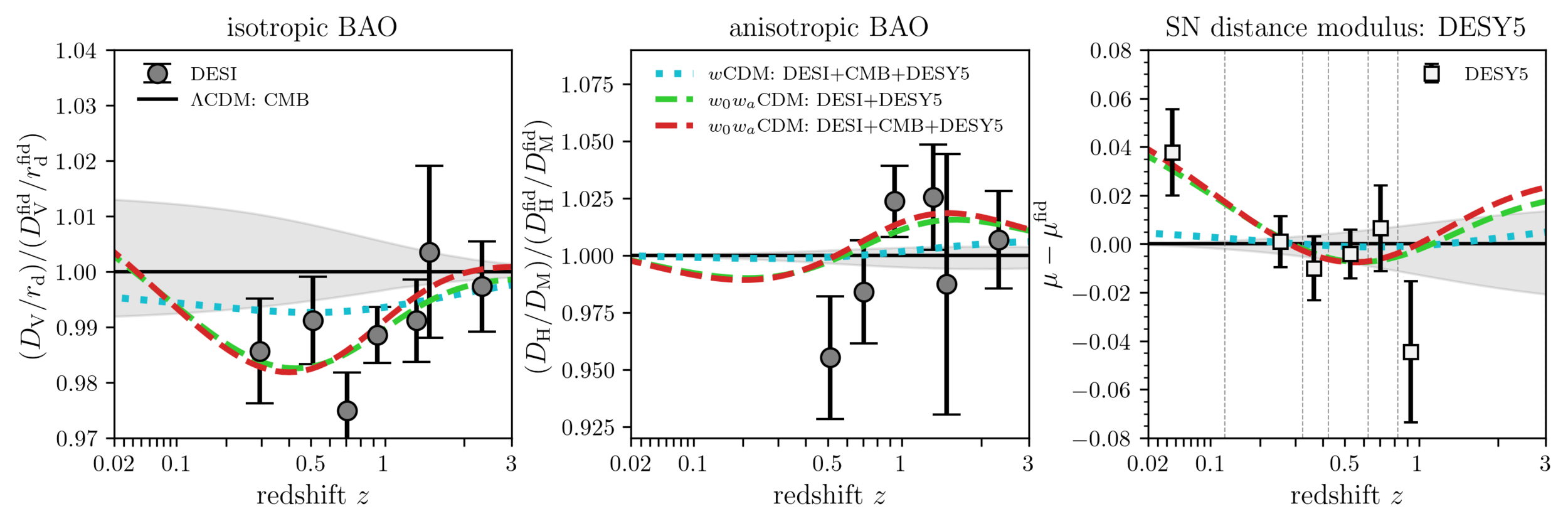
\(w_0w_a\mathrm{CDM}\) fits all 3 datasets!
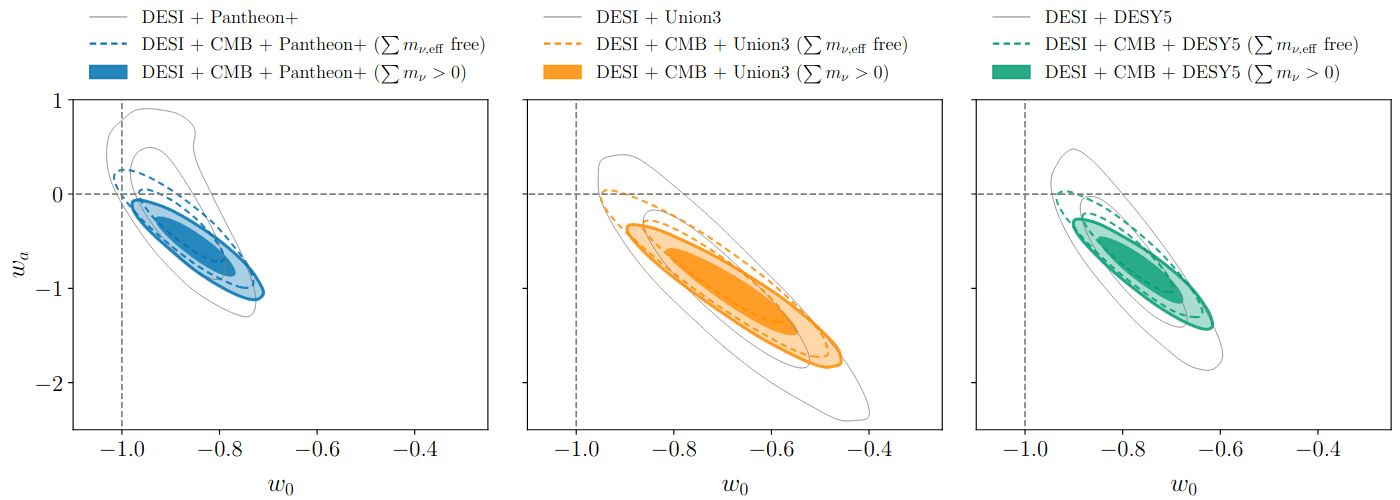
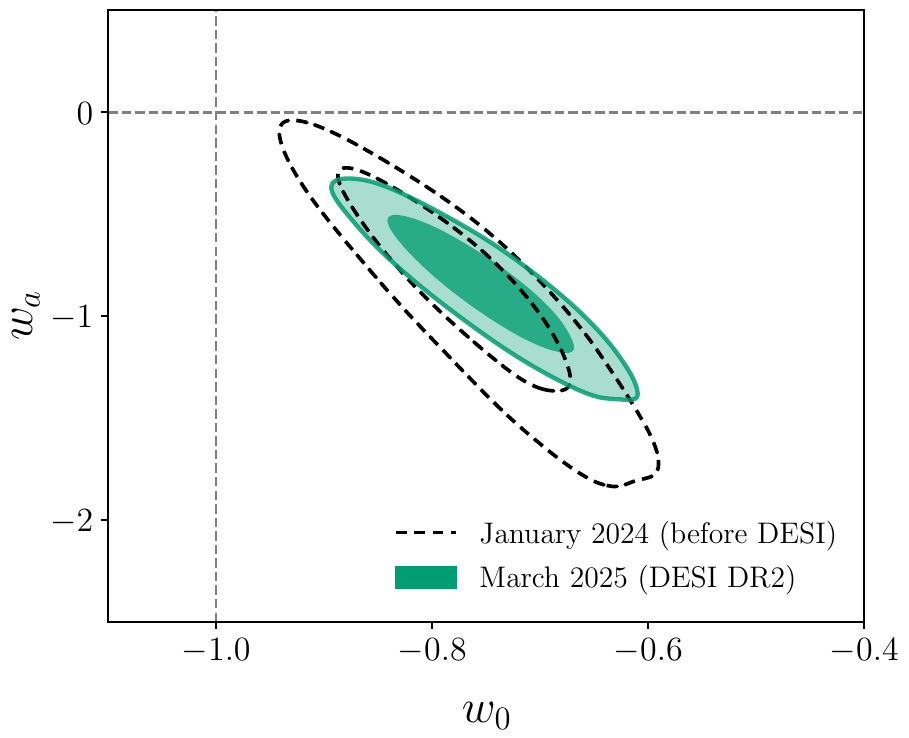
Dark Energy Evolution (\(w_0w_a\mathrm{CDM}\))
q(z)\equiv{-\frac{\ddot{a}a}{\dot{a}^2}}=\frac{d\ln H}{d\ln(1+z)}-1
Om(z)\equiv\frac{h^2(z)-1}{(1+z)^3-1}
f_{\rm DE}(z) \equiv \frac{\rho_\mathrm{DE}(z)}{\rho_\mathrm{DE,0}}
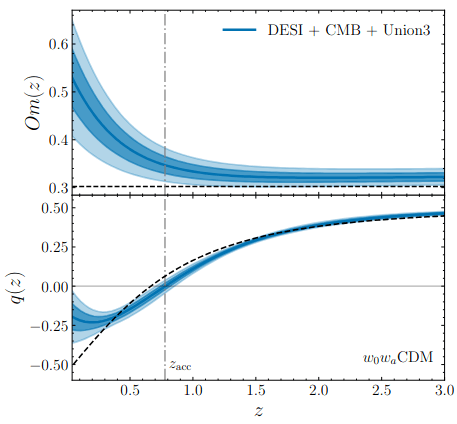
phantom
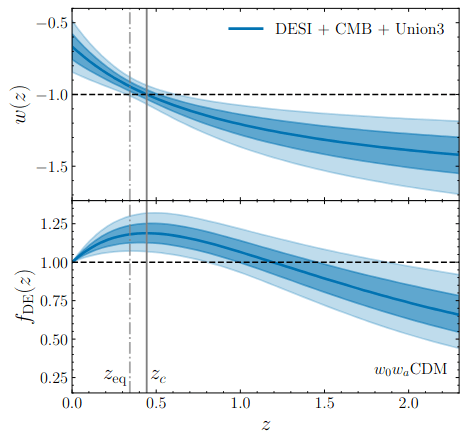
Dark Energy Evolution
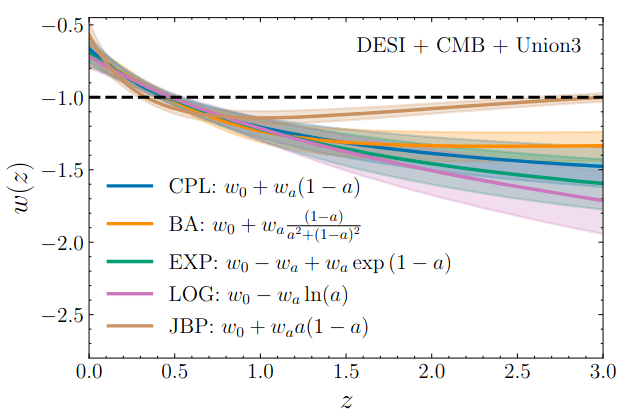
best described by CPL
\(4\sigma\)
Also considered: Gaussian Processes, similar evolution obtained
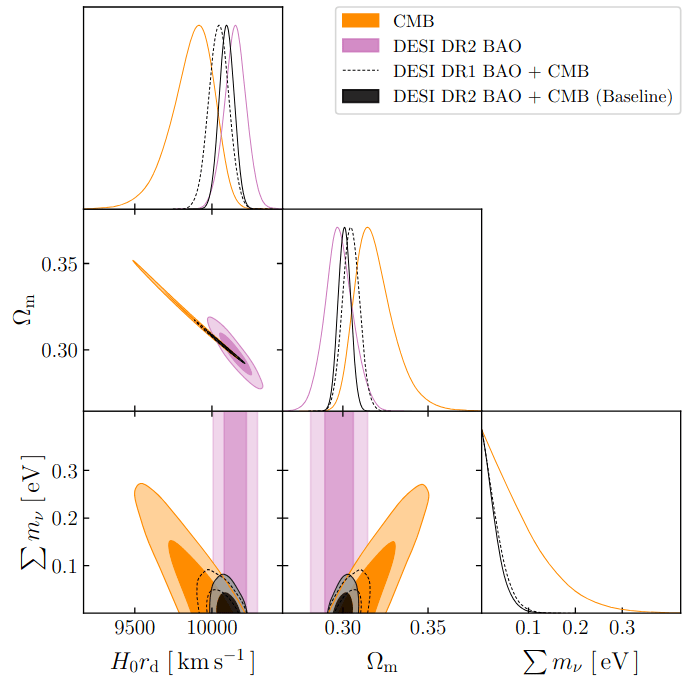
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO
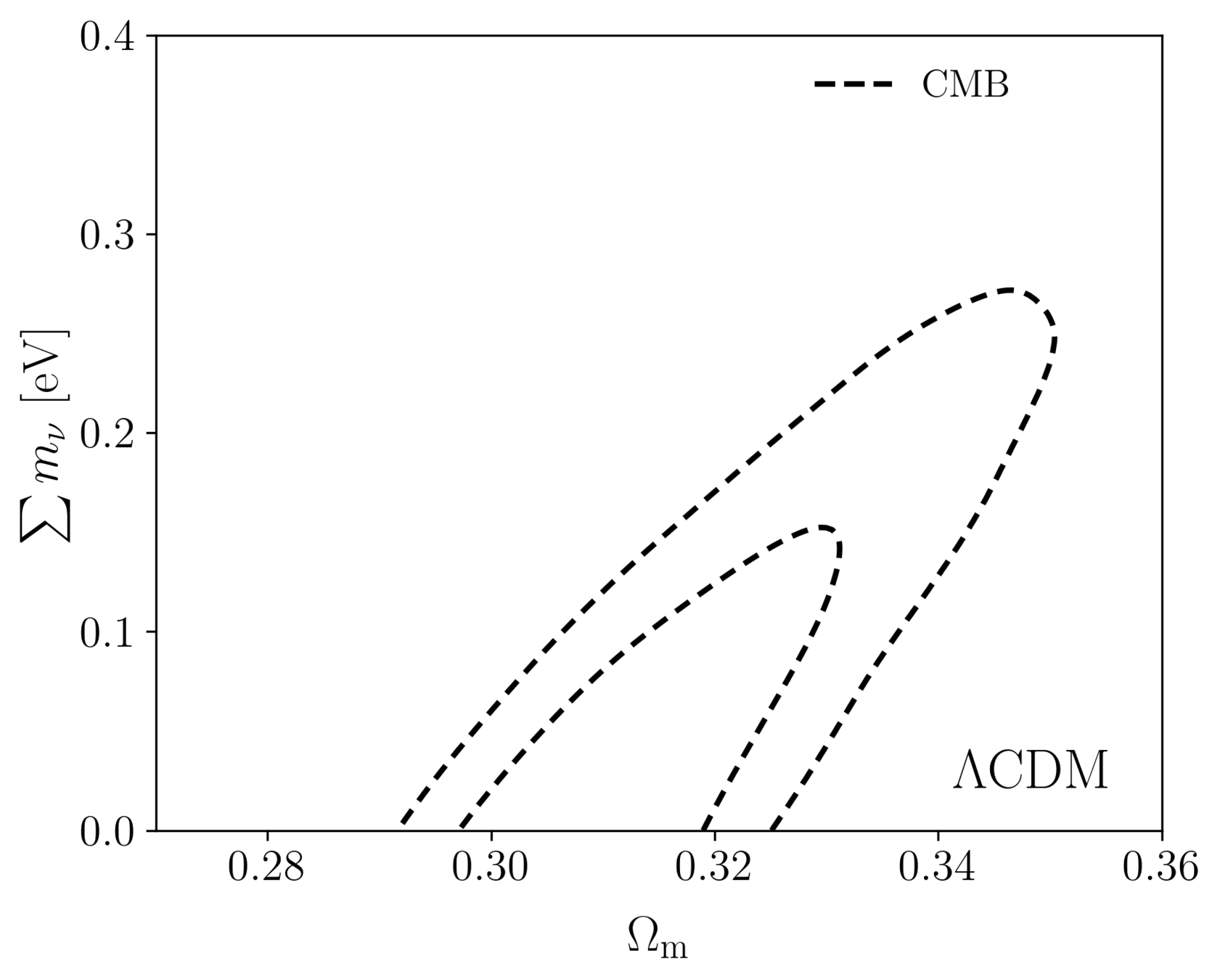
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
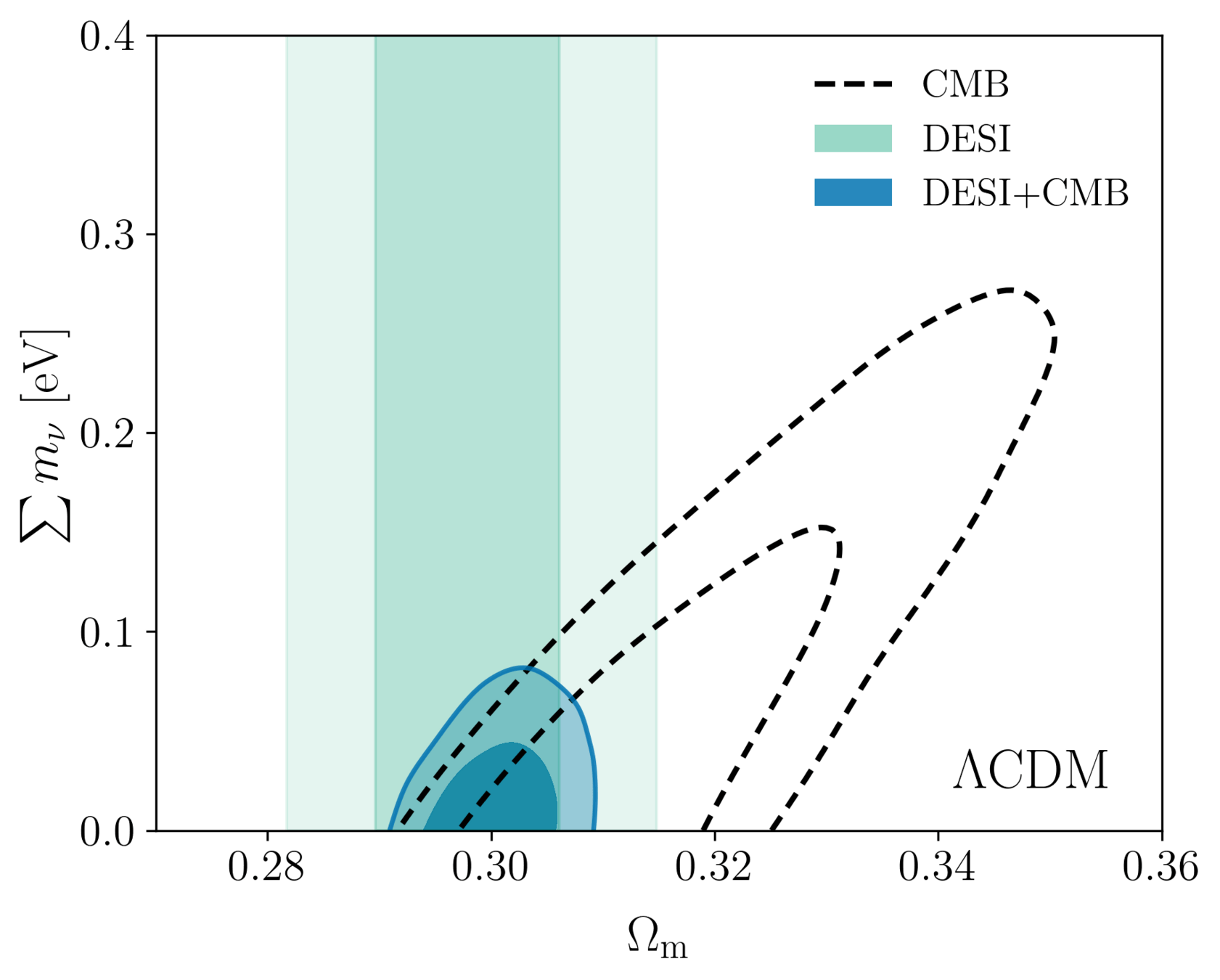
Broken by BAO, which favors low \(\Omega_\mathrm{m}\)
\sum m_\nu < 0.064 \, \mathrm{eV} \; (95\%, \text{DESI + CMB})
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO, which favors low \(\Omega_\mathrm{m}\)
\sum m_\nu < 0.064 \, \mathrm{eV} \; (95\%, \text{DESI + CMB})
Limit relaxed for \(w_0w_a\mathrm{CDM}\):
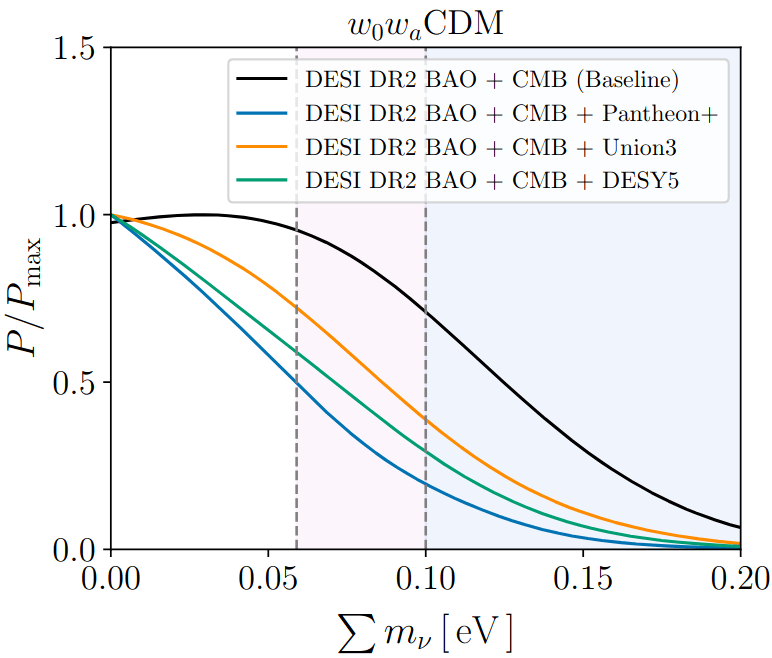
DESI+CMB: \(\sum m_\nu < 0.163 \, \mathrm{eV} \; (95\%)\)
DESI+CMB+DESY5: \(< 0.129 \, \mathrm{eV} \; (95\%)\)
Summary
DESI already has the most precise BAO measurements ever (40% more precise than DR1)
DESI in mild, growing, tension with CMB (\(2 - 3\sigma\)) and SN \((\sim 2\sigma)\) when interpreted in the ΛCDM model
Tightest upper bound on \(\sum m_\nu\), increasing tension with neutrino oscillations
Evidence for time-varying Dark Energy equation of state has increased with the DR2 BAO data by \(0.3\sigma\): CMB: \(3.1\sigma\), SN: \(2.8 - 4.2\sigma\), resolves \(\sum m_\nu\) tension
What I'm going to talk about
- The DESI survey
- The DR2 BAO analysis
- The cosmological constraints
- On-Going: DR2 Full Shape analysis
- My interests & my projects
\(\simeq 15\) min
Full Shape Analysis
We fit the "full shape" (FS) of the galaxy power spectrum multipoles
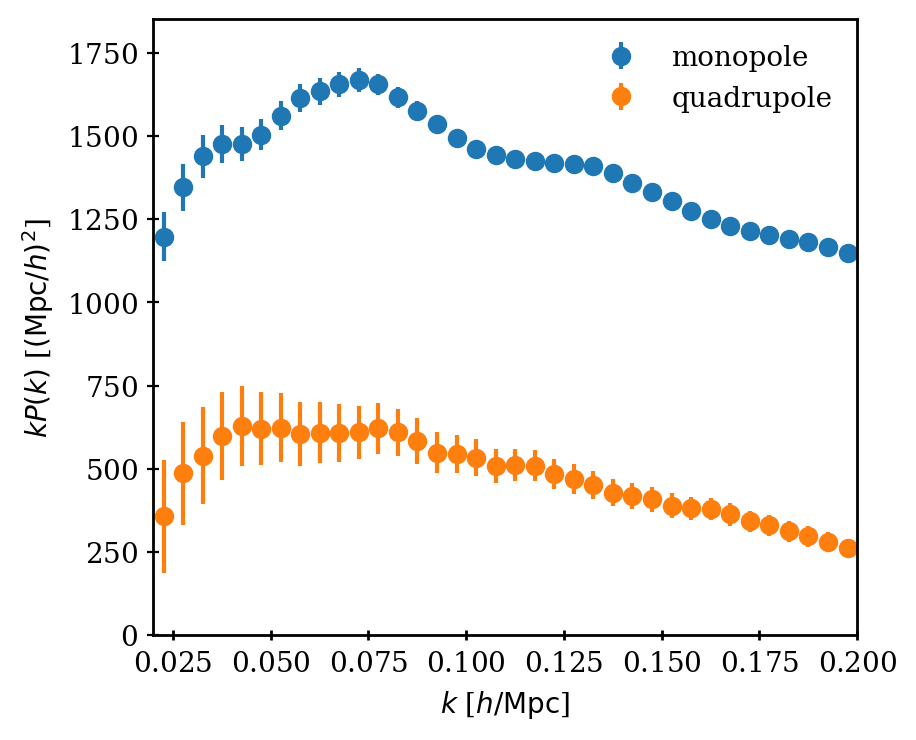
shape
(\( \Omega_\mathrm{cdm} h^2, \Omega_\mathrm{b} h^2, n_\mathrm{s}, \sum m_\nu \))
Full Shape Analysis
RSD
observed redshift = Hubble flow and peculiar velocities (RSD = "redshift space distortions")
v_\mathrm{pec} \propto f\sigma_8
shape
(\( \Omega_\mathrm{cdm} h^2, \Omega_\mathrm{b} h^2, n_\mathrm{s}, \sum m_\nu \))
growth of structure \(f\sigma_8\) sensitive to the theory of gravity and dark energy
Full Shape Analysis
real-space
Credit: Mathilde Pinon
Full Shape Analysis
redshift-space
Credit: Mathilde Pinon
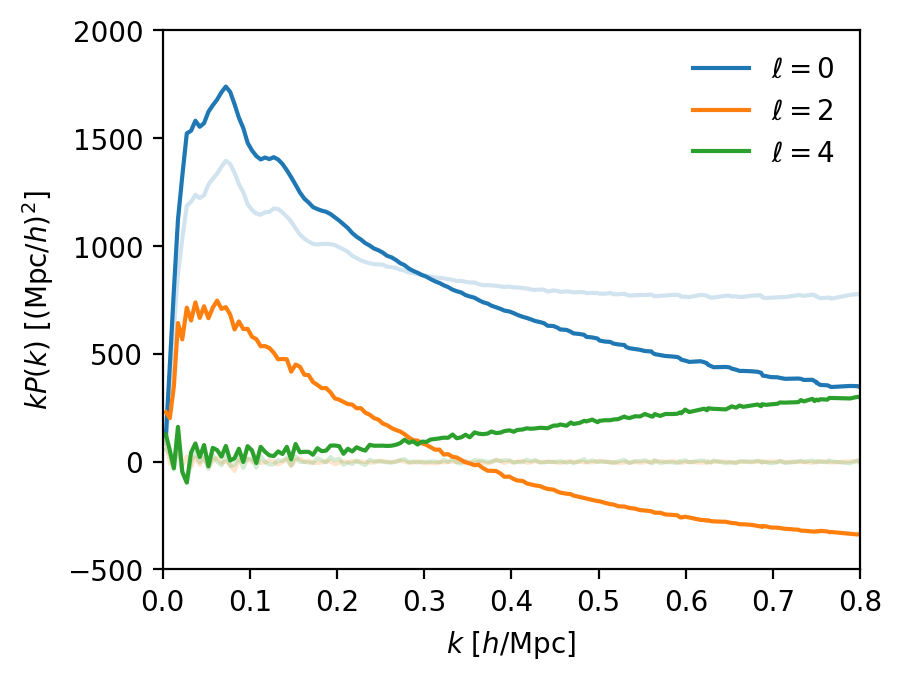
Full Shape Analysis
In November 2024: DR1 Full-Shape results (probing the growth of structure)
\(S_8 = \sigma_8(\Omega_\mathrm{m} / 0.3)^{0.5}\)
General Relativity
DR2 Full Shape analysis
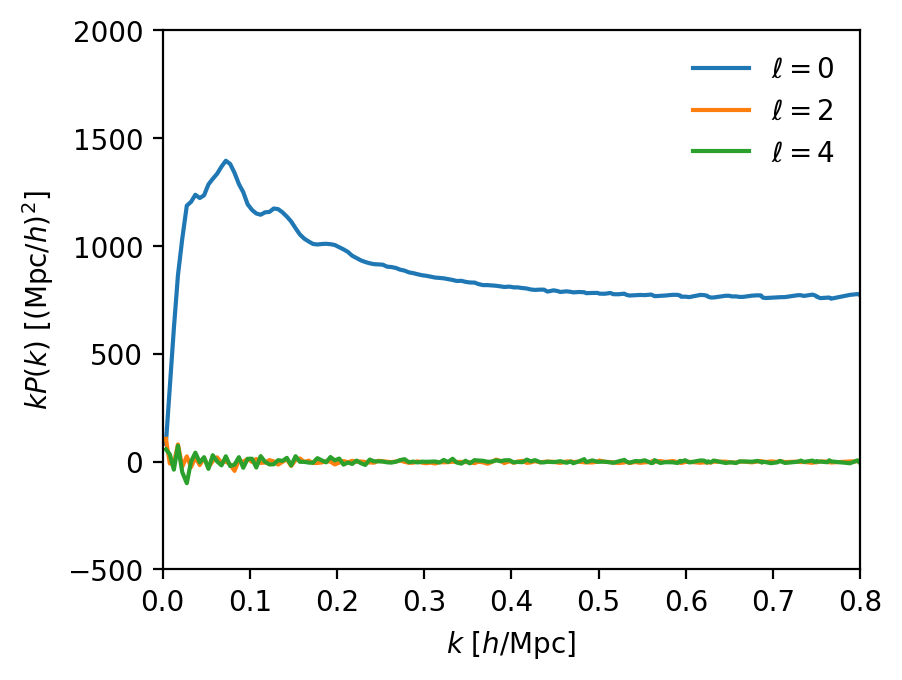
To the power spectrum \(\propto |\delta(\mathbf{k})|^2\)...
projection on \(\mathcal{L}_\ell(\hat{k} \cdot \hat{z})\)
DR2 Full Shape analysis
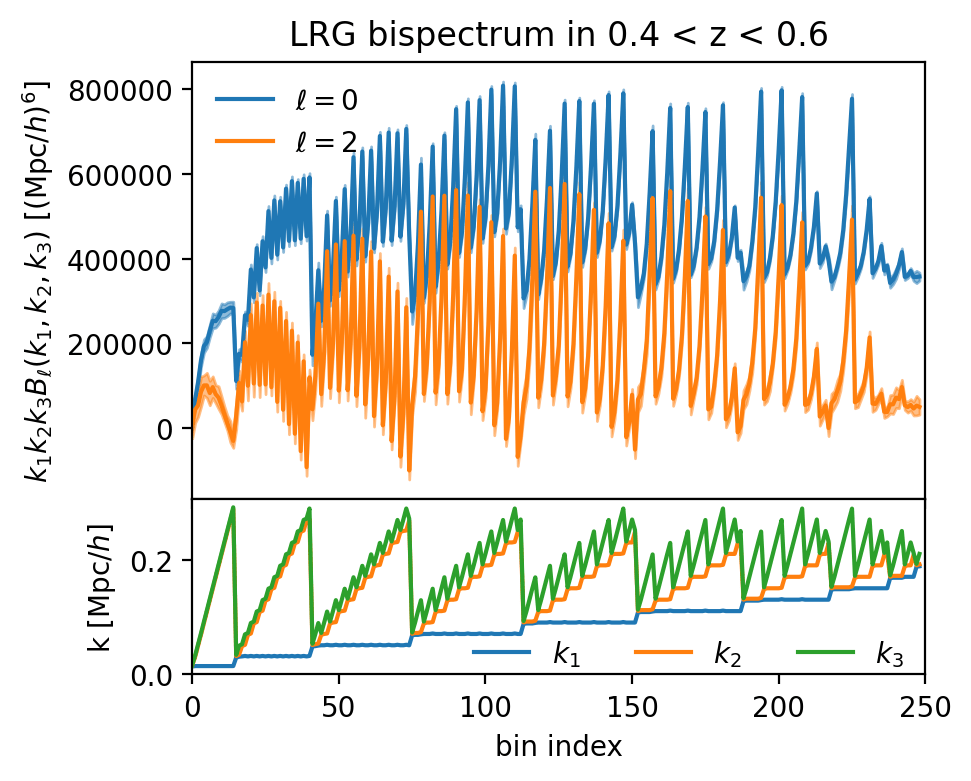
... we're adding the bispectrum \(\langle\delta(\mathbf{k_1})\delta(\mathbf{k_2})\delta(\mathbf{k_3})\rangle\)!
projection on \(\mathcal{L}_\ell(\hat{k}_3 \cdot \hat{z})\)
non-linearity of clustering
Scoccimarro15 basis
+
projection on \(\mathcal{L}_\ell(\hat{k} \cdot \hat{z})\)
DR2 Full Shape analysis
... we're adding the bispectrum \(\langle\delta(\mathbf{k_1})\delta(\mathbf{k_2})\delta(\mathbf{k_3})\rangle\)!
non-linearity of clustering
S_{\ell_1 \ell_2 L}(\hat{r}_1, \hat{r}_2, \hat{n}) =
H_{\ell_1\ell_2L}^{-1}
\sum_{m_1, m_2, M}
\begin{pmatrix}
\ell_1 & \ell_2 & L \\
m_1 & m_2 & M
\end{pmatrix}
y_{\ell_1 m_1}(\hat{r}_1)
y_{\ell_2 m_2}(\hat{r}_2)
y_{L M}(\hat{n})
+
projection on \(\mathcal{L}_\ell(\hat{k} \cdot \hat{z})\)
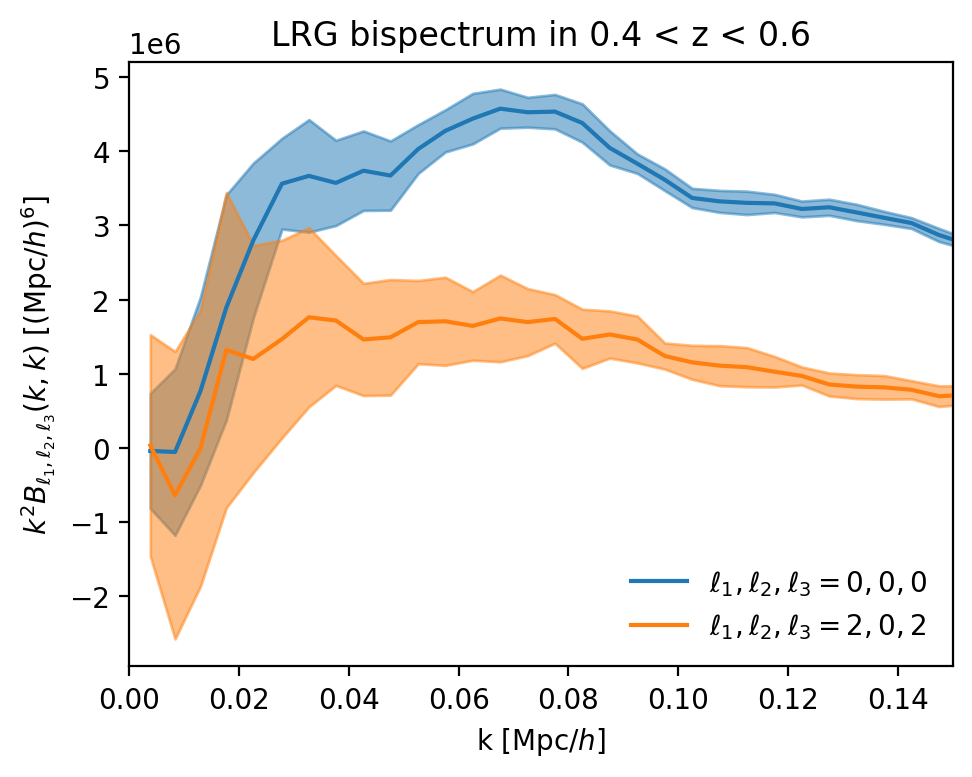
projection on:
DR2 mock challenge
Tests of different models with N-body simulation boxes
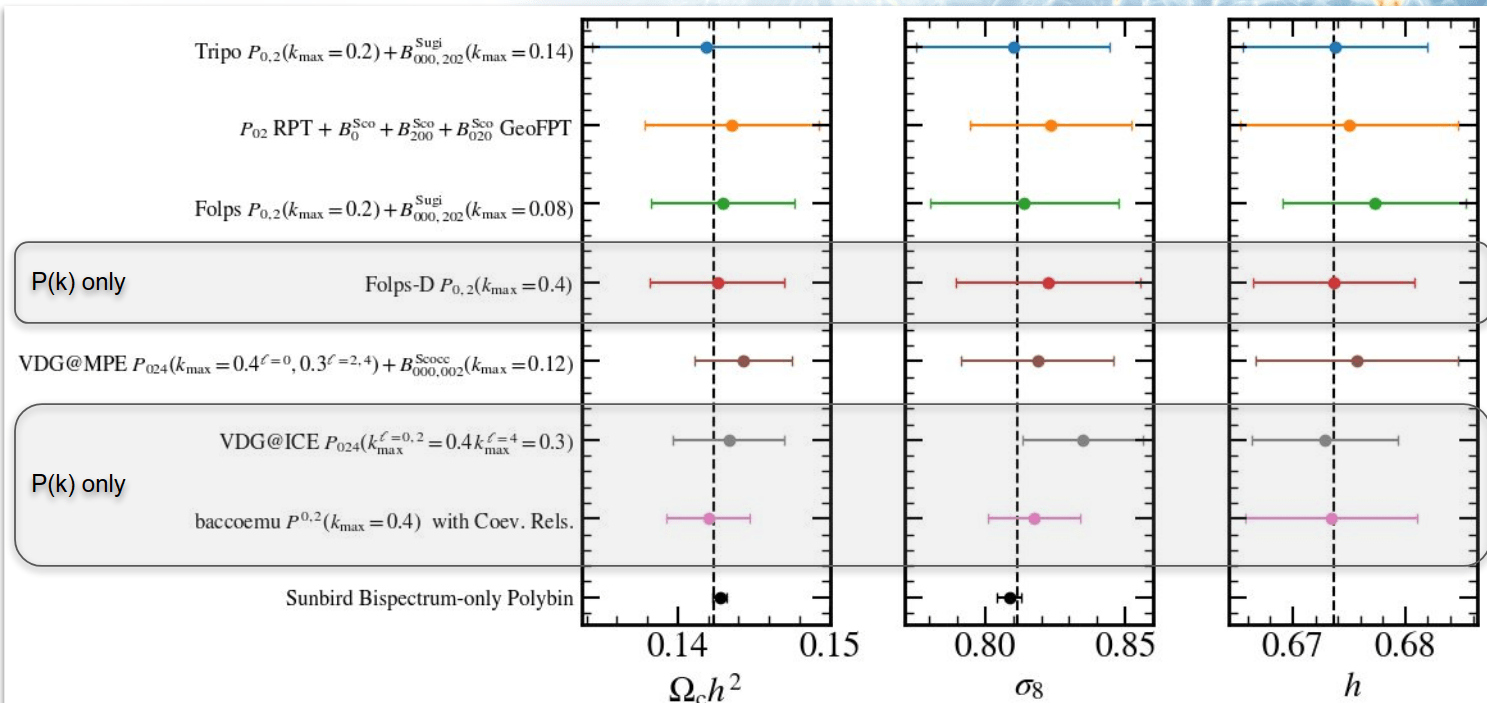
PT
semi-PT
simulation-based
PRELIMINARY
Why is Full Shape challenging?
\(F(\mathbf{r}) = n_g(\mathbf{r}) - \bar{n}(\mathbf{r}) = \bar{n}(\mathbf{r})\delta_g(\mathbf{r})\)
selection function
observed density of galaxies
Full shape of the galaxy power spectrum (and now bispectrum!) sensitive to:
- the survey geometry
\(F(\mathbf{r}) = n_g(\mathbf{r}) - \bar{n}(\mathbf{r}) = \bar{n}(\mathbf{r})\delta_g(\mathbf{r})\)
selection function
observed density of galaxies
Full shape of the galaxy power spectrum (and now bispectrum!) sensitive to:
- the survey geometry
Why is Full Shape challenging?
\bar{n}_\mathrm{rad}(z)
\bar{n}_\mathrm{sky}(\mathrm{R.A.}, \mathrm{Dec.})
\(\propto\) number of (random) galaxy pairs as a function of separation
smoothing effect
Full shape of the galaxy power spectrum (and now bispectrum!) sensitive to:
- the survey geometry
Why is Full Shape challenging?
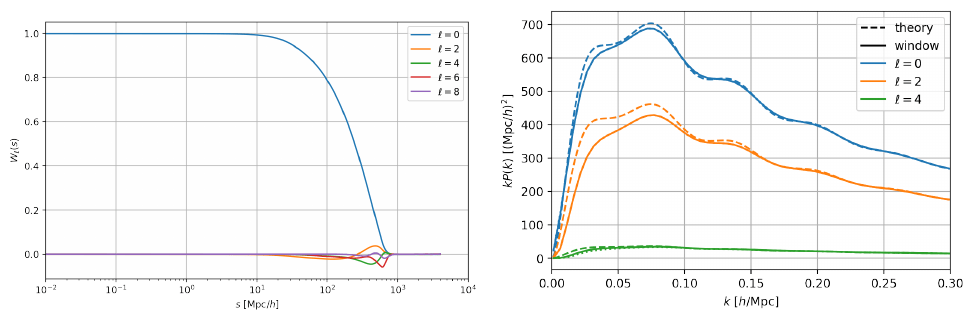
\(\langle P_o(k) \rangle = W(k, k^\prime) P_t(k^\prime)\)
"window matrix"
Full shape of the galaxy power spectrum (and now bispectrum!) sensitive to:
- the survey geometry
- (mis)specification of the selection function \(\bar{n}\) = "observational systematics"
Why is Full Shape challenging?
Full shape of the galaxy power spectrum (and now bispectrum!) sensitive to:
- the survey geometry
-
(mis)specification of the selection function \(\bar{n}\) = "observational systematics"
- photometry: "how many targets are selected depending on observing conditions" (e.g. Rosado-Marin+25)
- fiber assignment: "not all targets receive a fiber" (e.g. Bianchi+25)
- spectroscopy: "not all redshifts are measured reliably" (e.g. Krolewski+25) and "uncertainty on the redshift measurement" (e.g. Yu+25)
Why is Full Shape challenging?
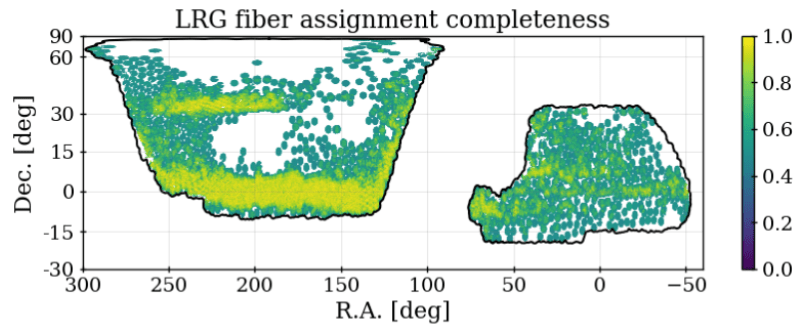
Fiber assignment
Groups of galaxies too close to each other cannot all receive a fiber
\(0.05^\circ \simeq\) positioner patrol diameter
focal plane
Fiber assignment: mitigation
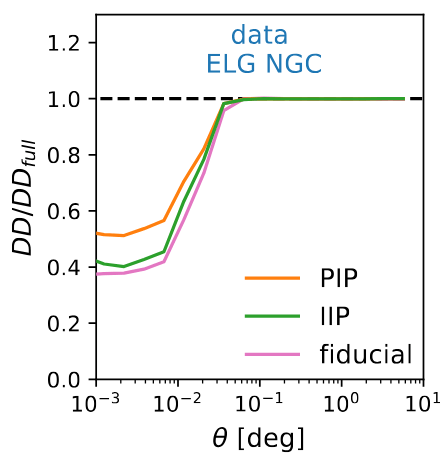
\(\theta\)-cut = remove all pairs \(< 0.05^\circ\)
w/ fiber assignment
Mathilde Pinon
Fiber assignment: mitigation
New window matrix \(W^\mathrm{cut}\); \(\langle P_o(k) \rangle = W^\mathrm{cut}(k, k^\prime) P_t(k^\prime)\)
Very non diagonal: let's "rotate" it
more compact
Fiber assignment: mitigation
pairwise inverse probability weights (PIP) and angular upweighting (AUW) (e.g. Bianchi and Percival 2017)
w_\mathrm{PIP} = 1/\text{prob. of pair being selected}
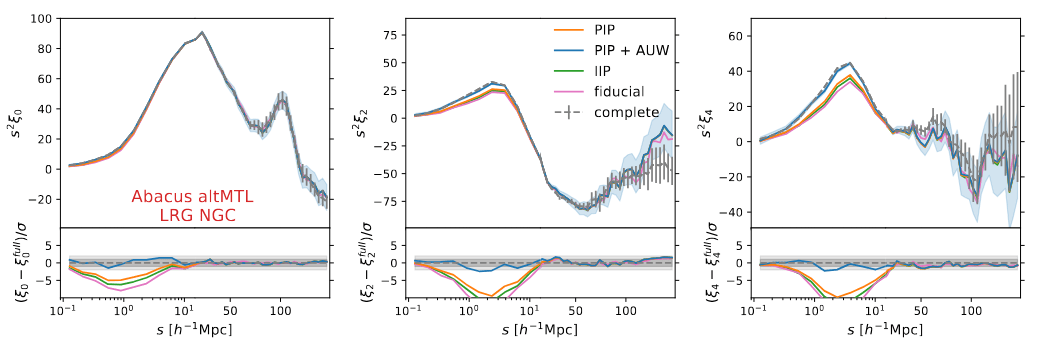
well-corrected
What else?
With DR2 - stay tuned!
- Full-Shape from power spectrum and bispectrum
- Primordial non-Gaussianity
- x CMB lensing
- Low-\(z\) growth of structure with peculiar velocities
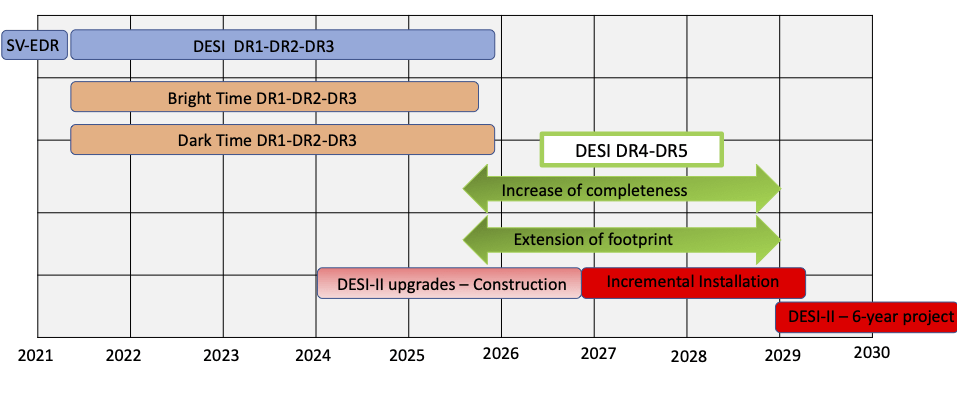
- DR1-DR2-DR3: 5-year nominal survey, almost completed
- DR4-DR5: ~ 3.5-year transition period
- DESI-II: Dark Matter, high-density and high-z programs
What else?
- broadly speaking, DESI galaxy clustering and cosmology pipeline
- leveraging Python library JAX (GPU, jit, autodiff) to do cool stuffs
- faster \(P(k), B(k)\) estimators with multi-GPU
Personal interests
Forward-modeled window matrix \(W(k_o, k_t) = dP_o(k_o)/dP_t(k_t)\) to include "survey complexity"
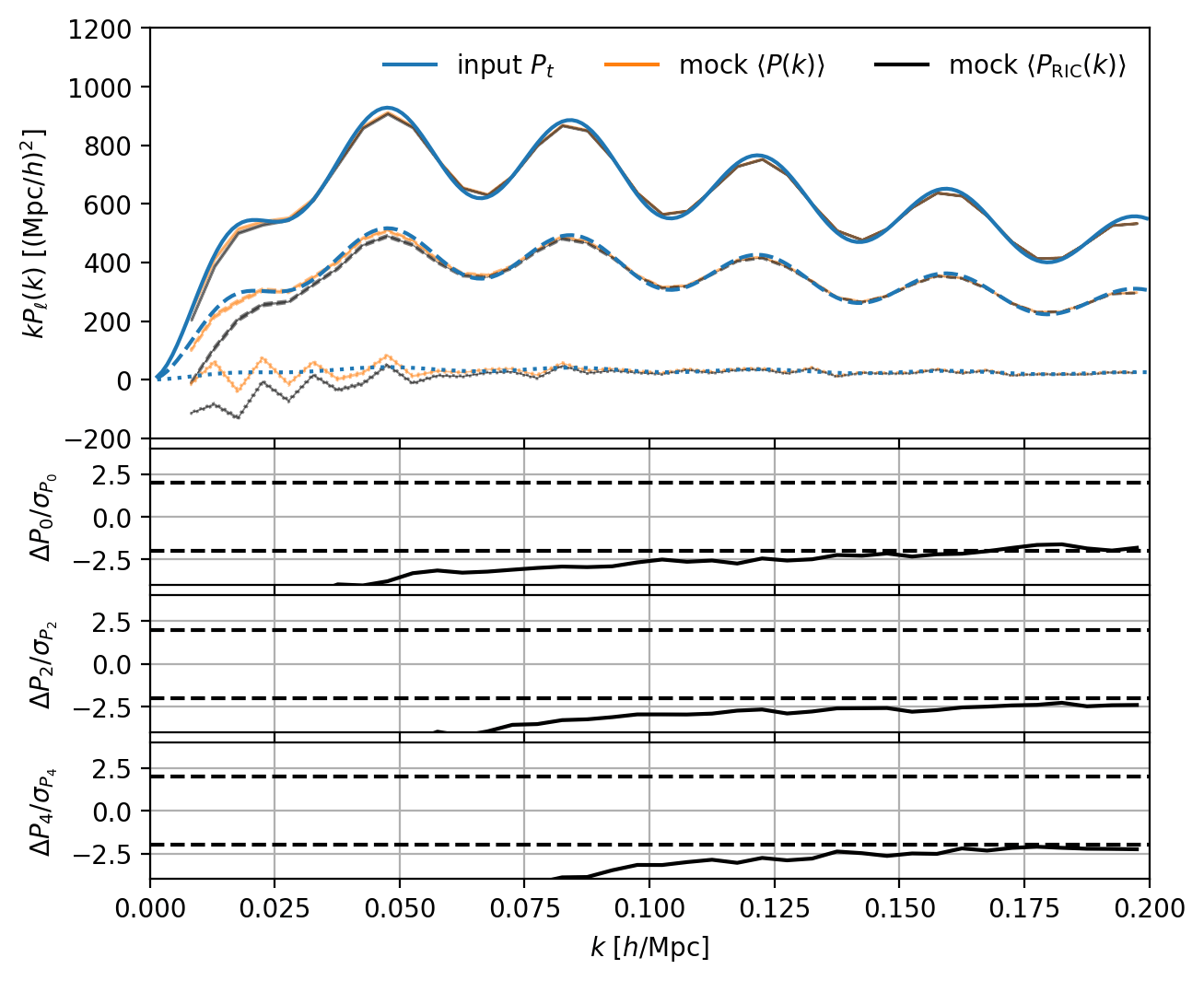
RIC
\(\sigma/\sqrt{1000}\)
directly measured from data
\(\Rightarrow \int d^2\hat{r} F(\hat{r}) = 0\)
\(\equiv\) Radial Integral Constraint (RIC)
Window matrix
\overbrace{\bar{n}_\mathrm{rad}(z)\bar{n}_\mathrm{sky}(\mathrm{R.A.}, \mathrm{Dec.})}{}
F(\mathbf{r}) = n_g(\mathbf{r}) - \bar{n}(\mathbf{r})
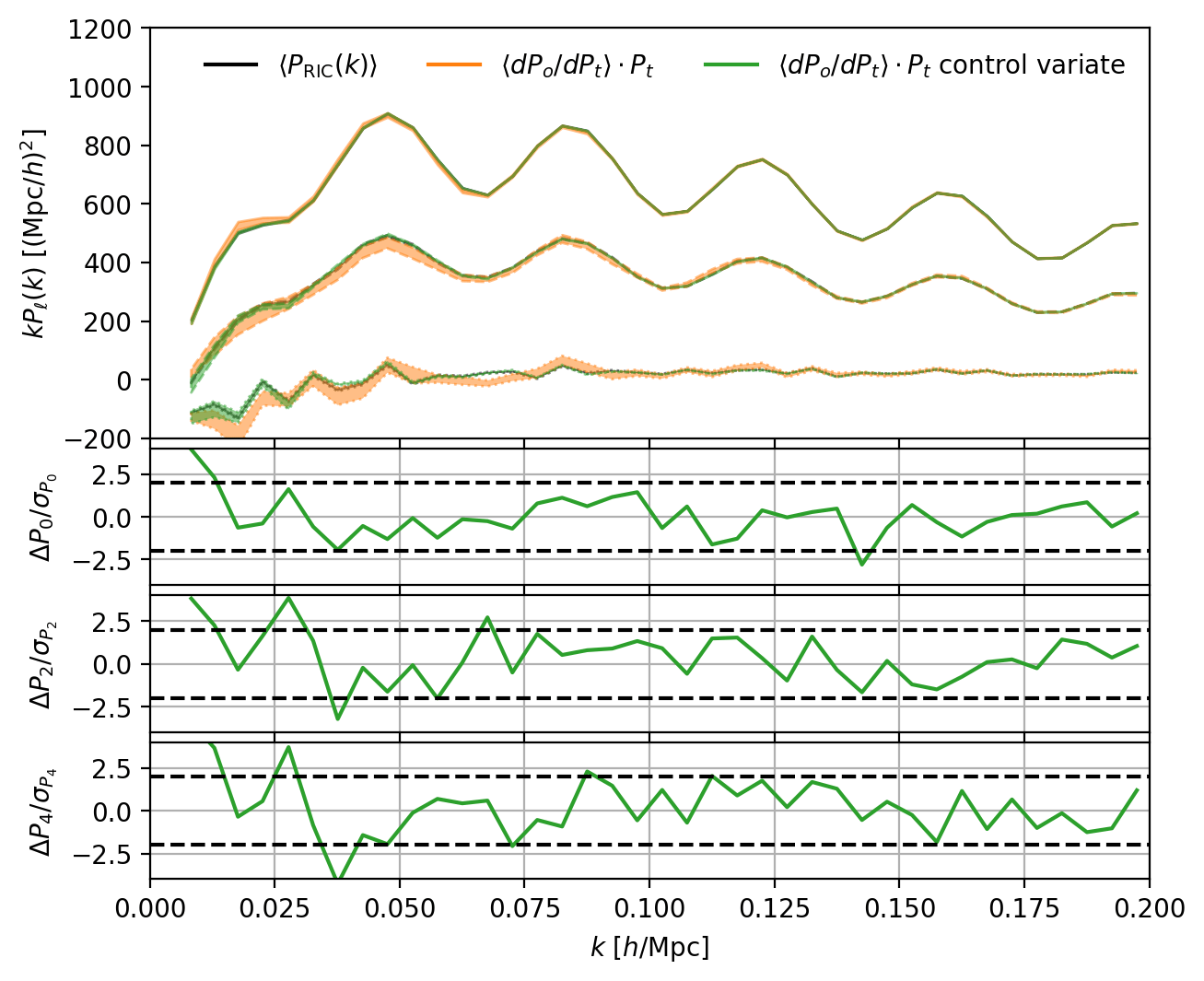
with just 25 mocks
- "brute-force" algorithm: create mocks with \(P_t\) zero everywhere except for given \(k_t\) \(\Rightarrow\) \(W(k_o, k_t)\) given by \(<P_o(k_o)>\)
- control variate: computing the "exact" window matrix for \(\delta \rightarrow \delta W\) is tractable; then one can just estimate the window matrix of the difference of \(P_o(k)\) with and without RIC
Window matrix
Pair counts on the GPU
- for PIP/AUW weights (mitigation of fiber assignment)
- extended to galaxy-shear and shear-shear correlations: an order of magnitude faster than state-of-the-art
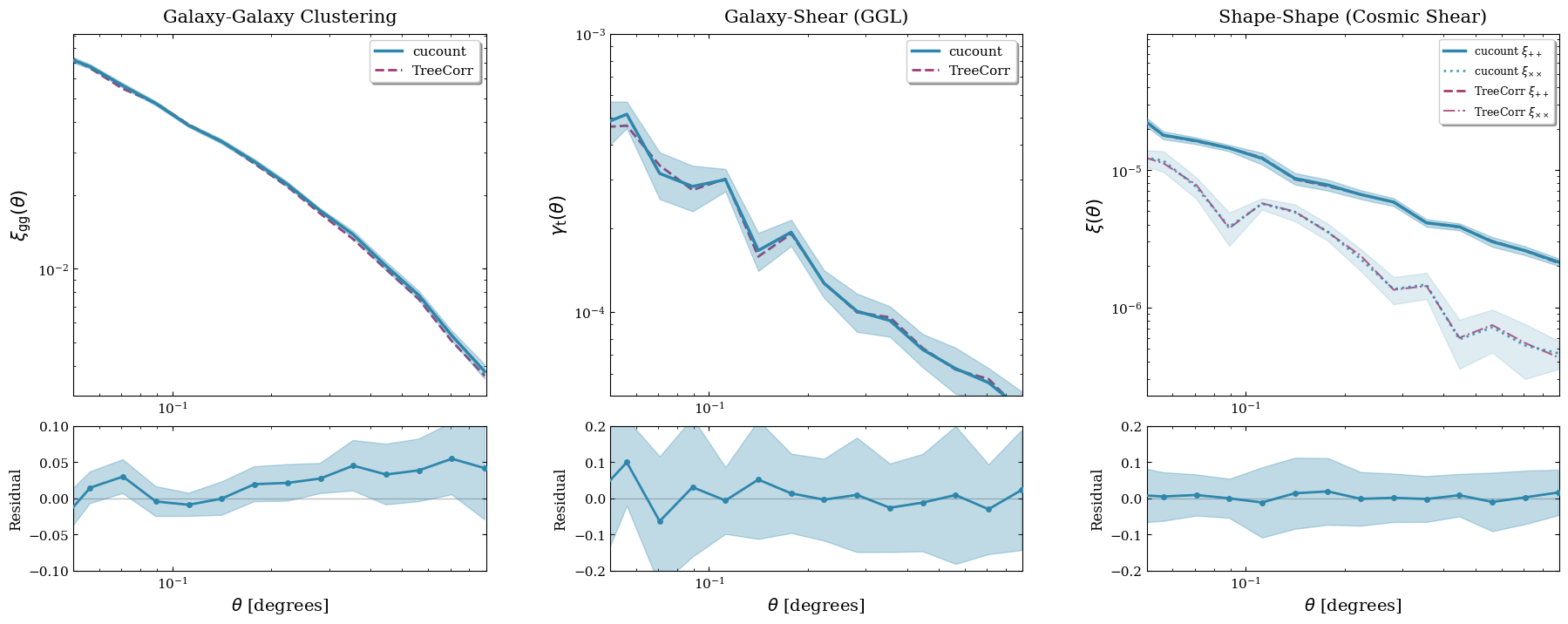
Calum Murray
Pair counts on the GPU
# Initialize distributed environment
jax.distributed.initialize()
from cucount.jax import BinAttrs, count2
# Define binning and line-of-sight
battrs = BinAttrs(s=np.linspace(1., 201, 201), mu=(np.linspace(-1., 1., 201), 'midpoint'))
# Create sharding mesh: divides array on multiple GPUs
mesh = Mesh(jax.devices(), axis_names=('x',))
# Define parallel pair-count function
count2_parallel = shard_map(
lambda p1, p2: jax.lax.psum(count2(p1, p2, battrs=battrs), axis_name='x'),
mesh=mesh,
in_specs=(P('x'), P(None)), # Shard only one input
out_specs=P(None)
)
# Run distributed pair counts
counts = count2_parallel(particles1, particles2)
jax.distributed.shutdown()Looking forward: triplet counts? autodiff for fitting data at small scale? (e.g.: HOD fits)
Field-level inference
Fit the observed (discretized) field
Sample the initial cosmic density field
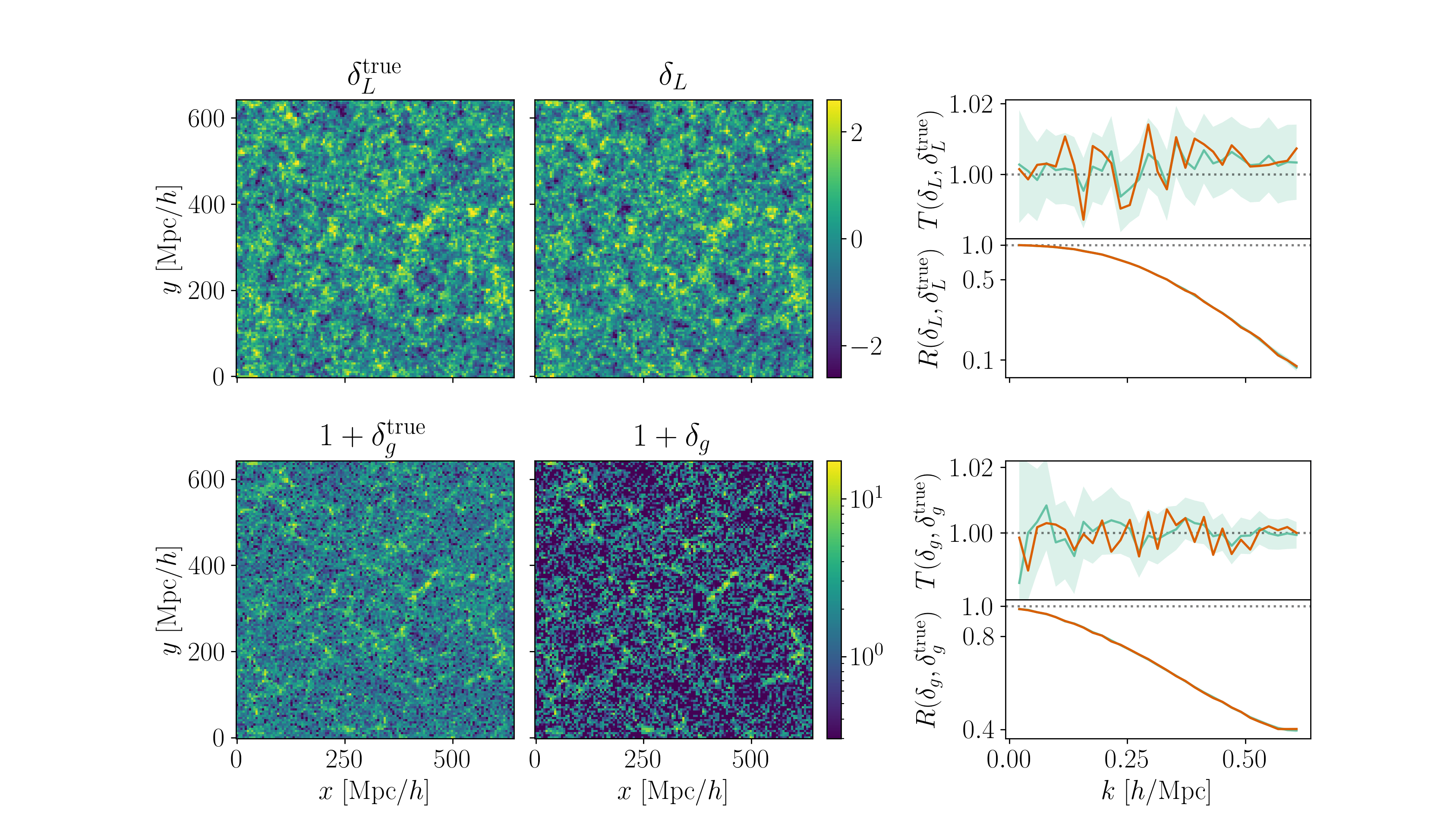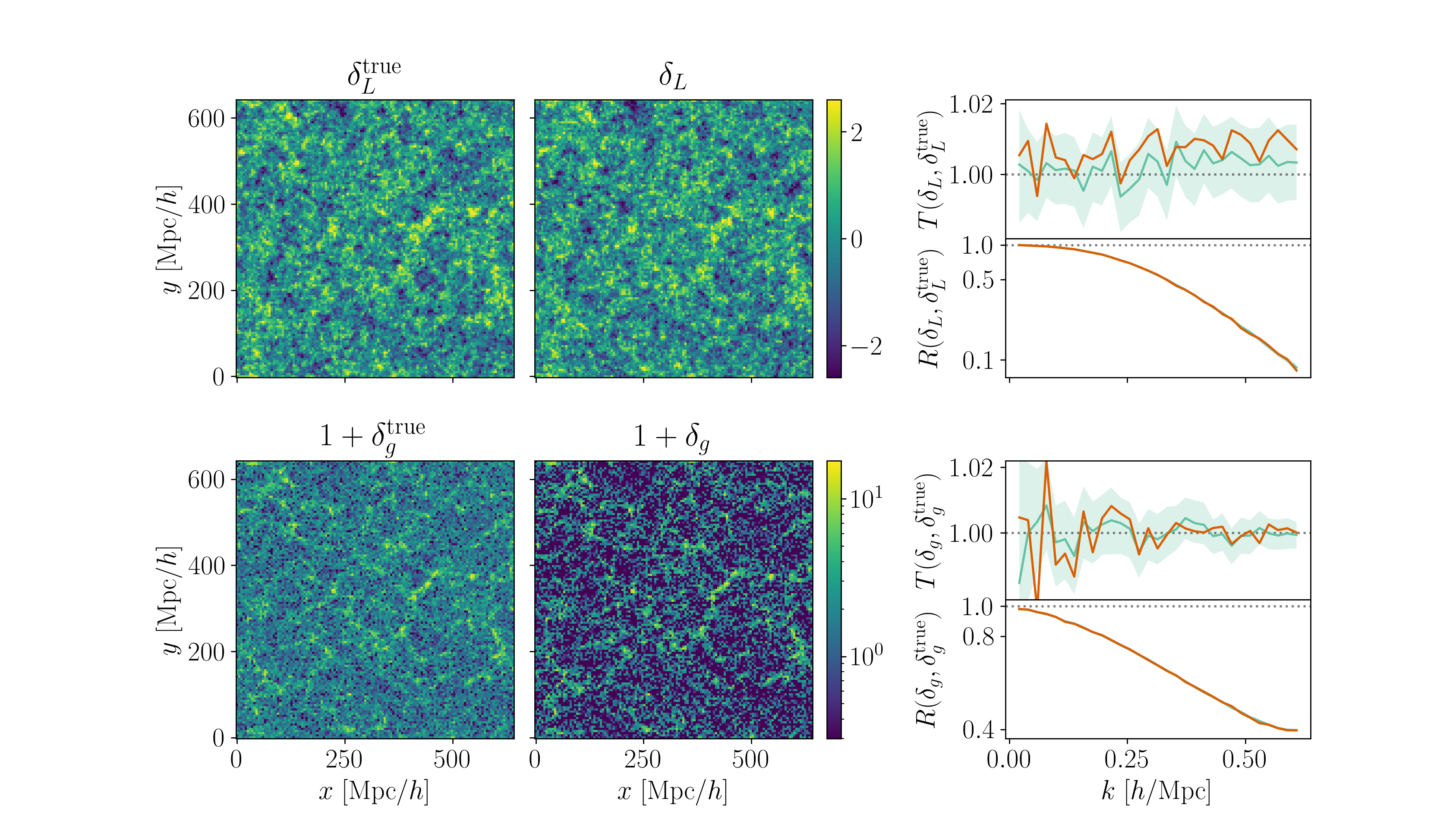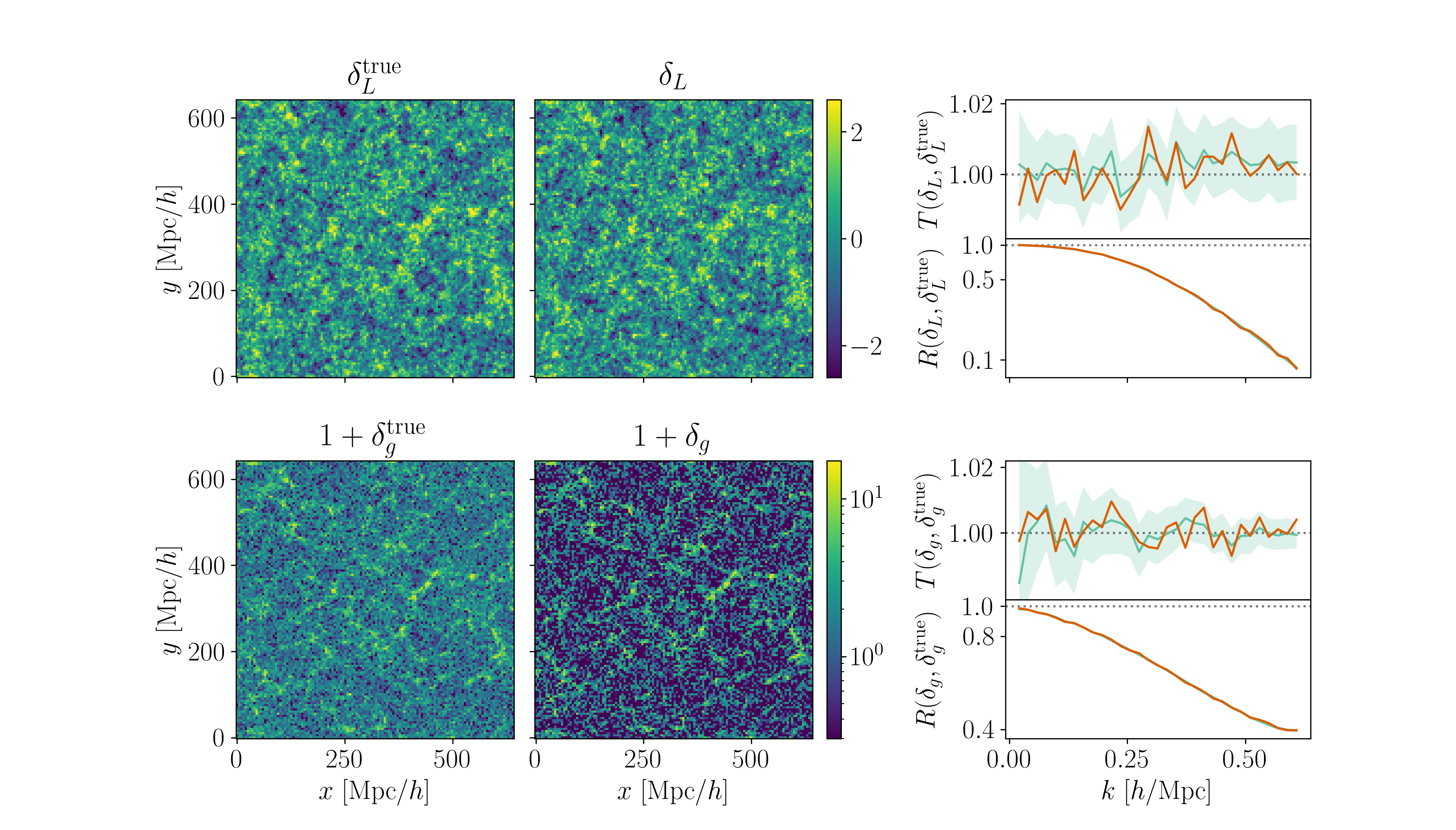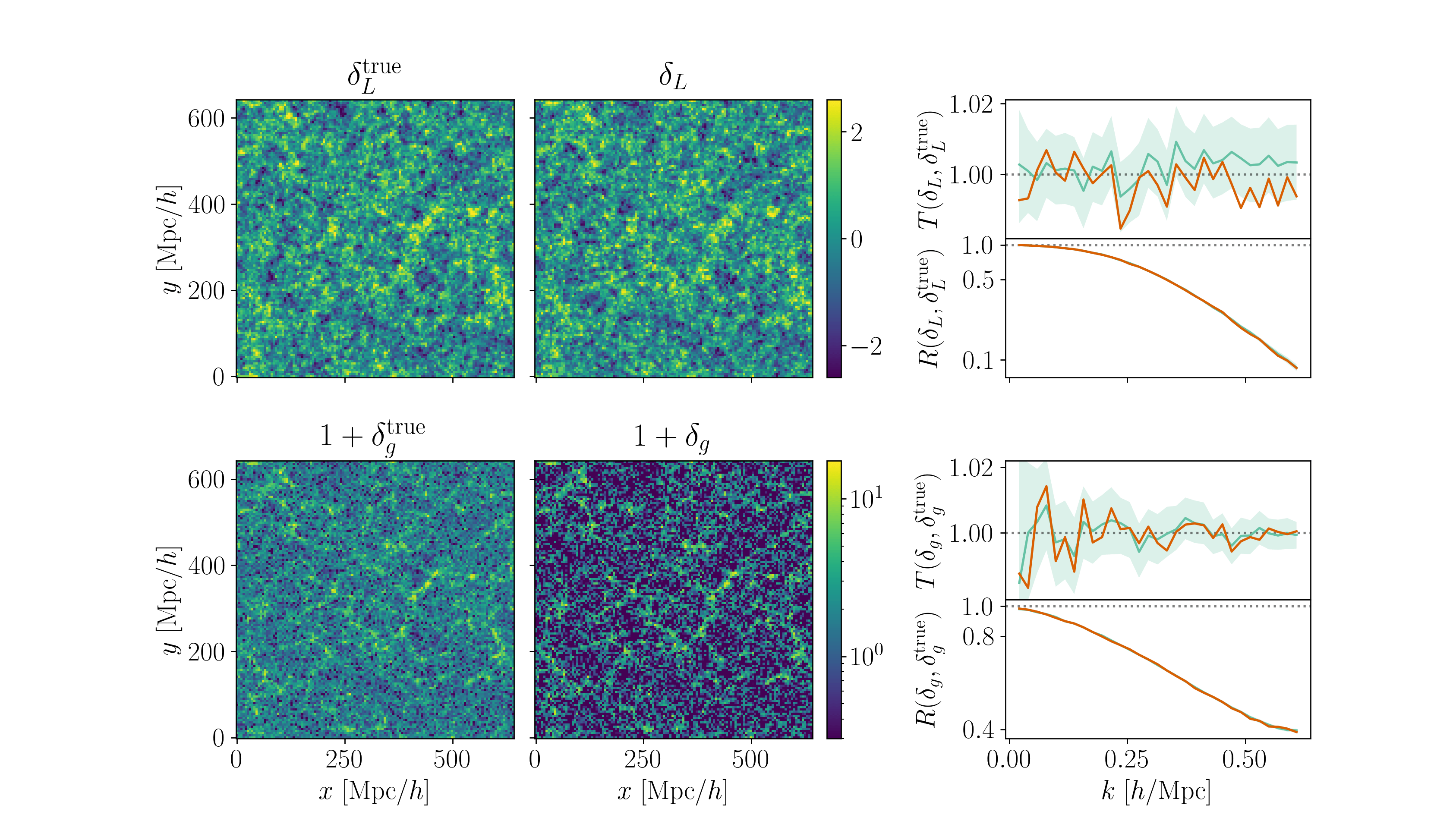
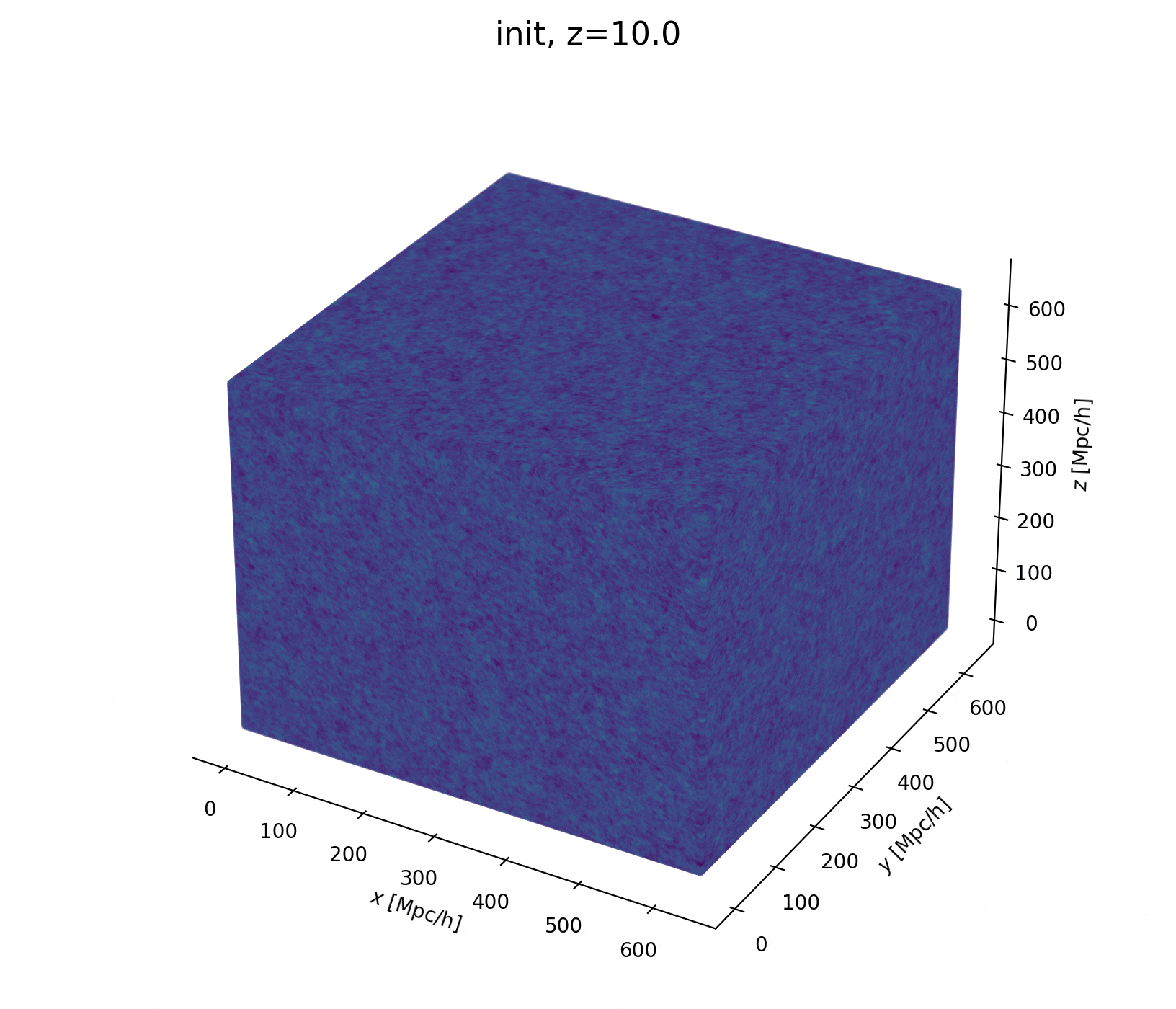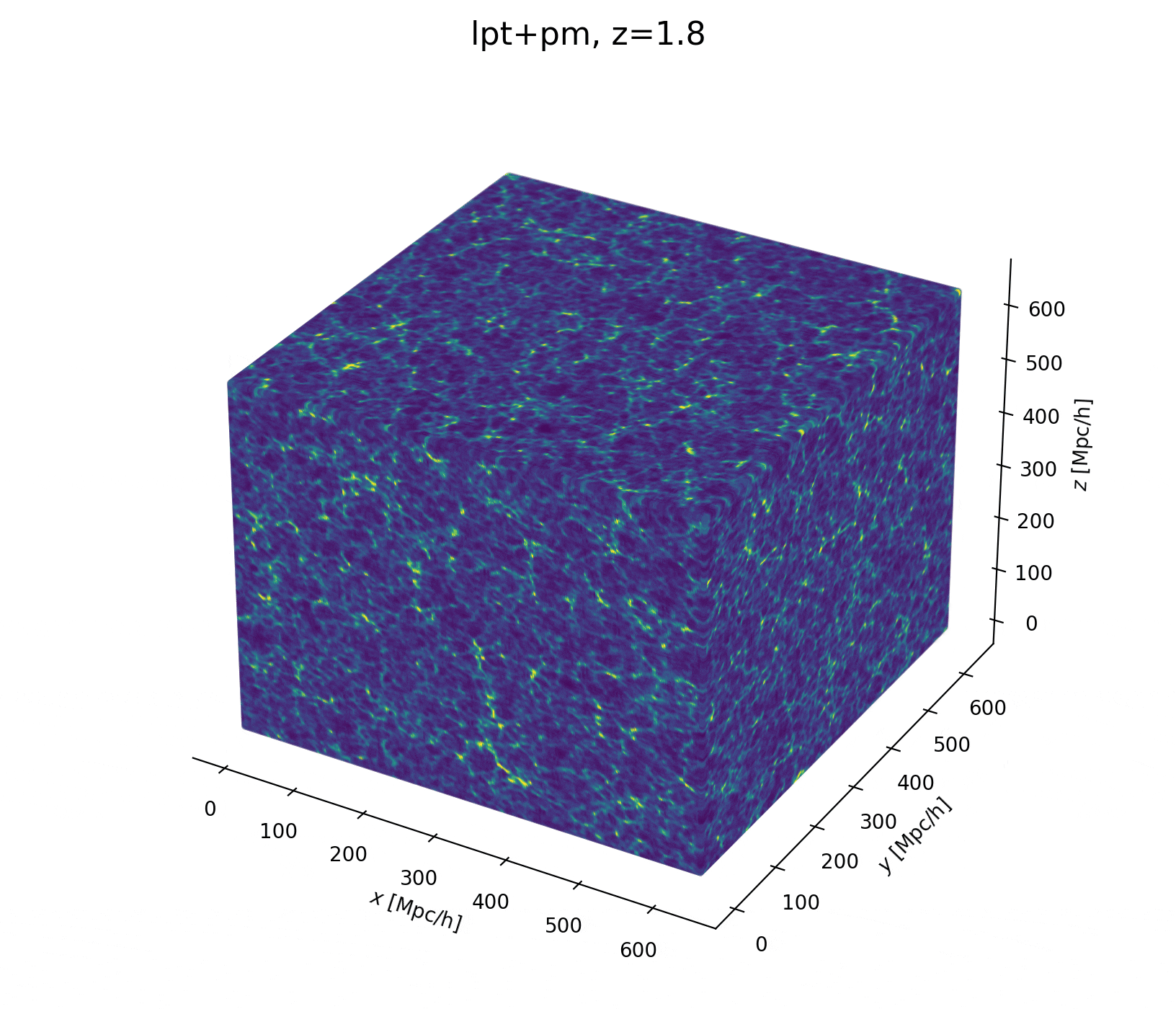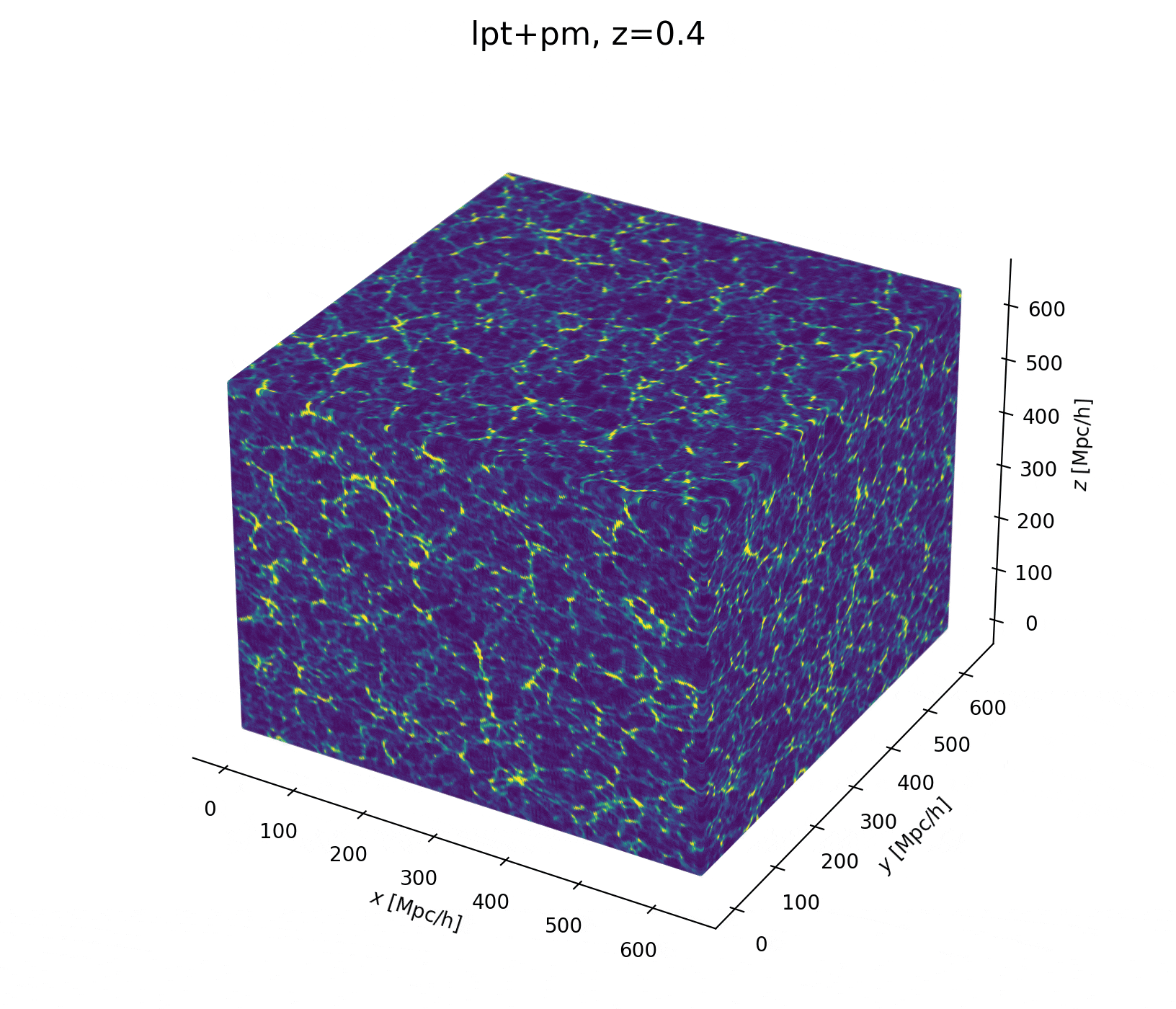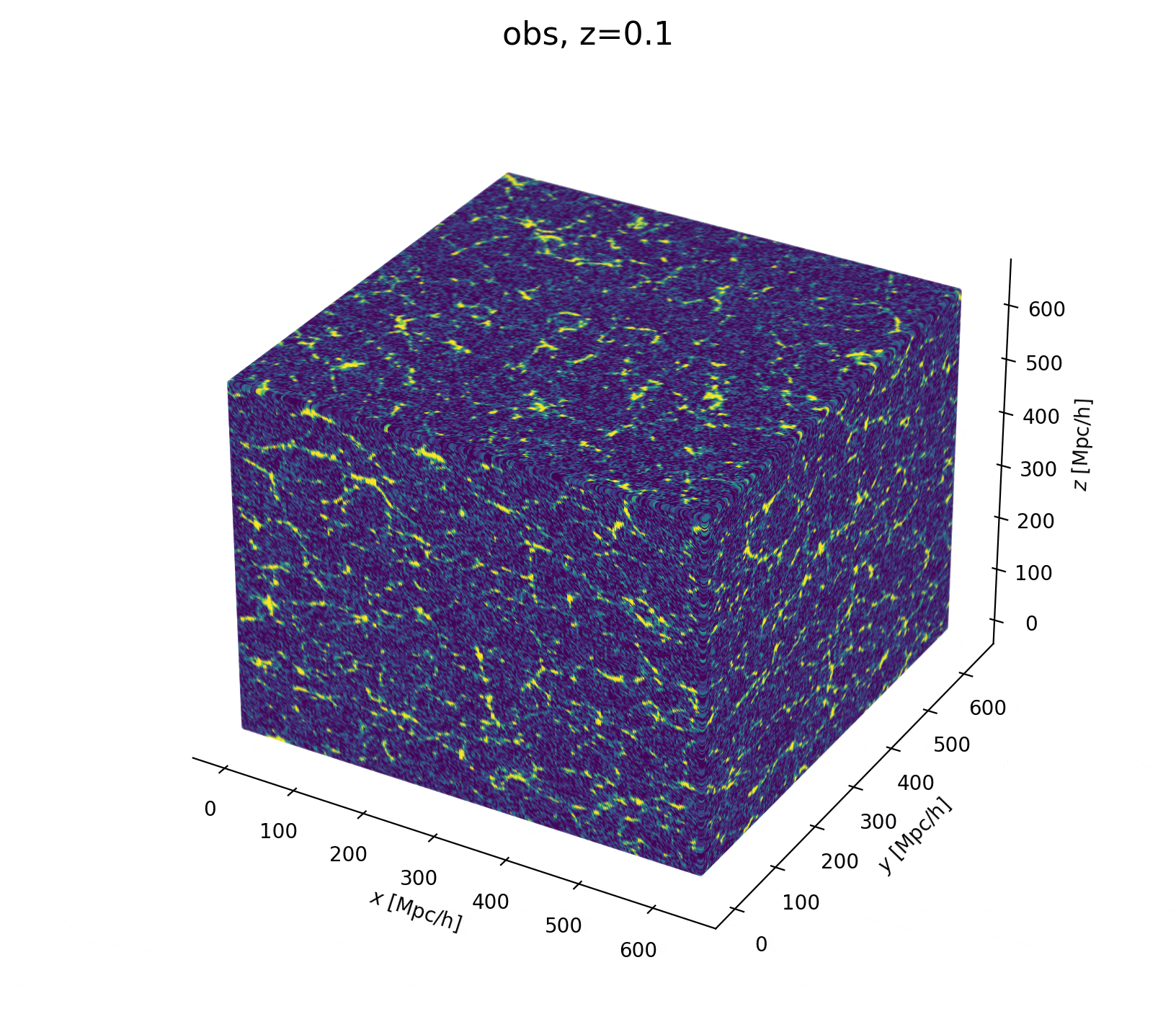
initial density
final density
Hugo Simon, co-supervisor François Lanusse
Field-level inference (benchmark)
gradient-based samplers
unadjusted
more efficient
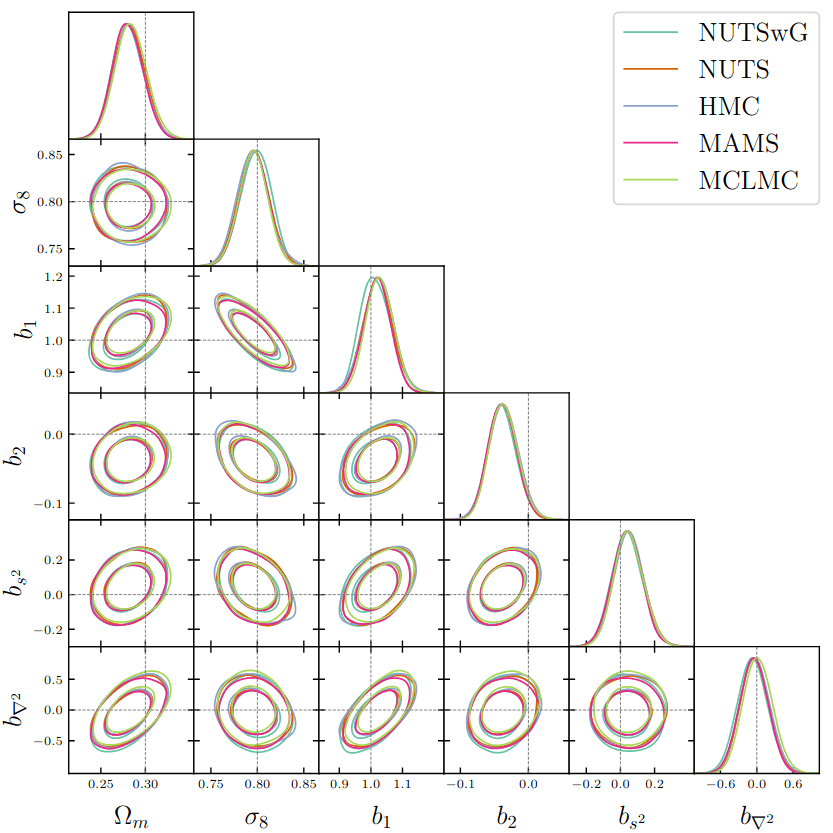
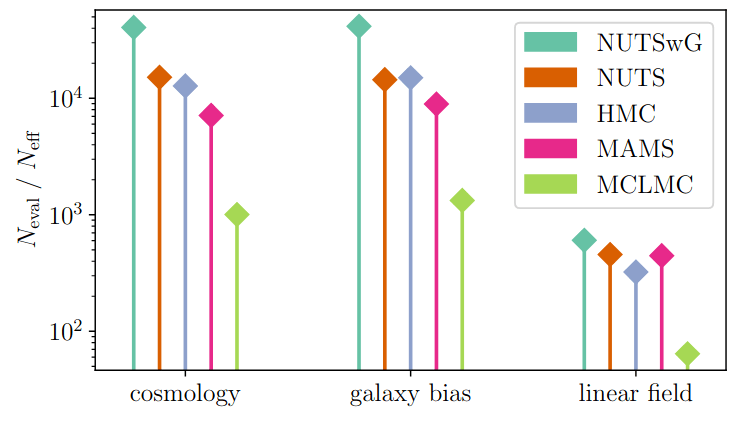
Field-level inference (benchmark)
gradient-based samplers
more efficient
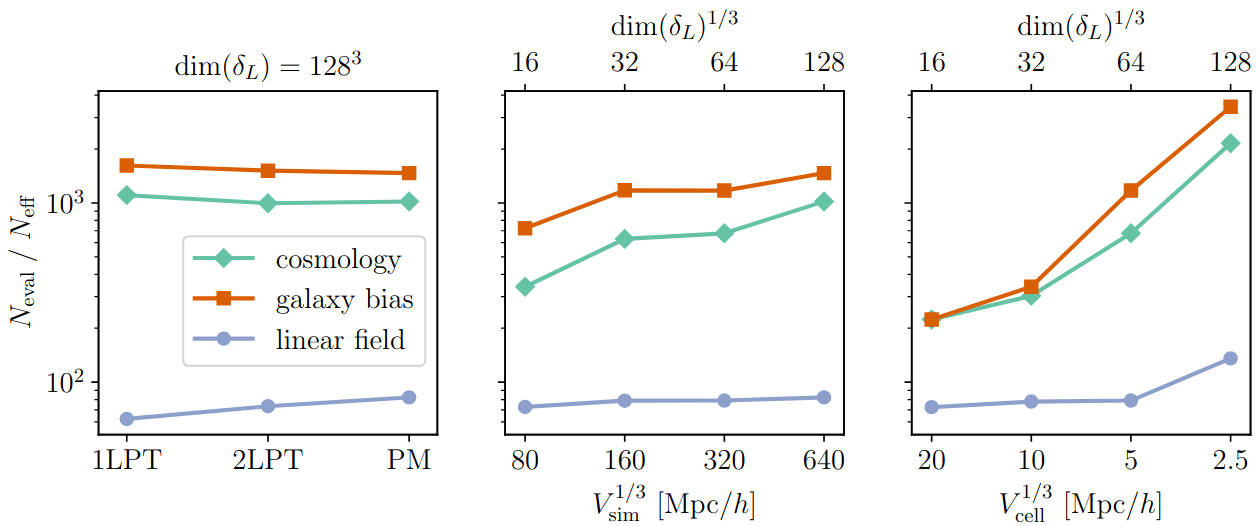
efficiency almost constant with dimension
\(10^6\) parameters \(\simeq 8\) GPU hours
Field-level inference (PNG)
Goal: measure primordial non-Gaussianity with DESI data
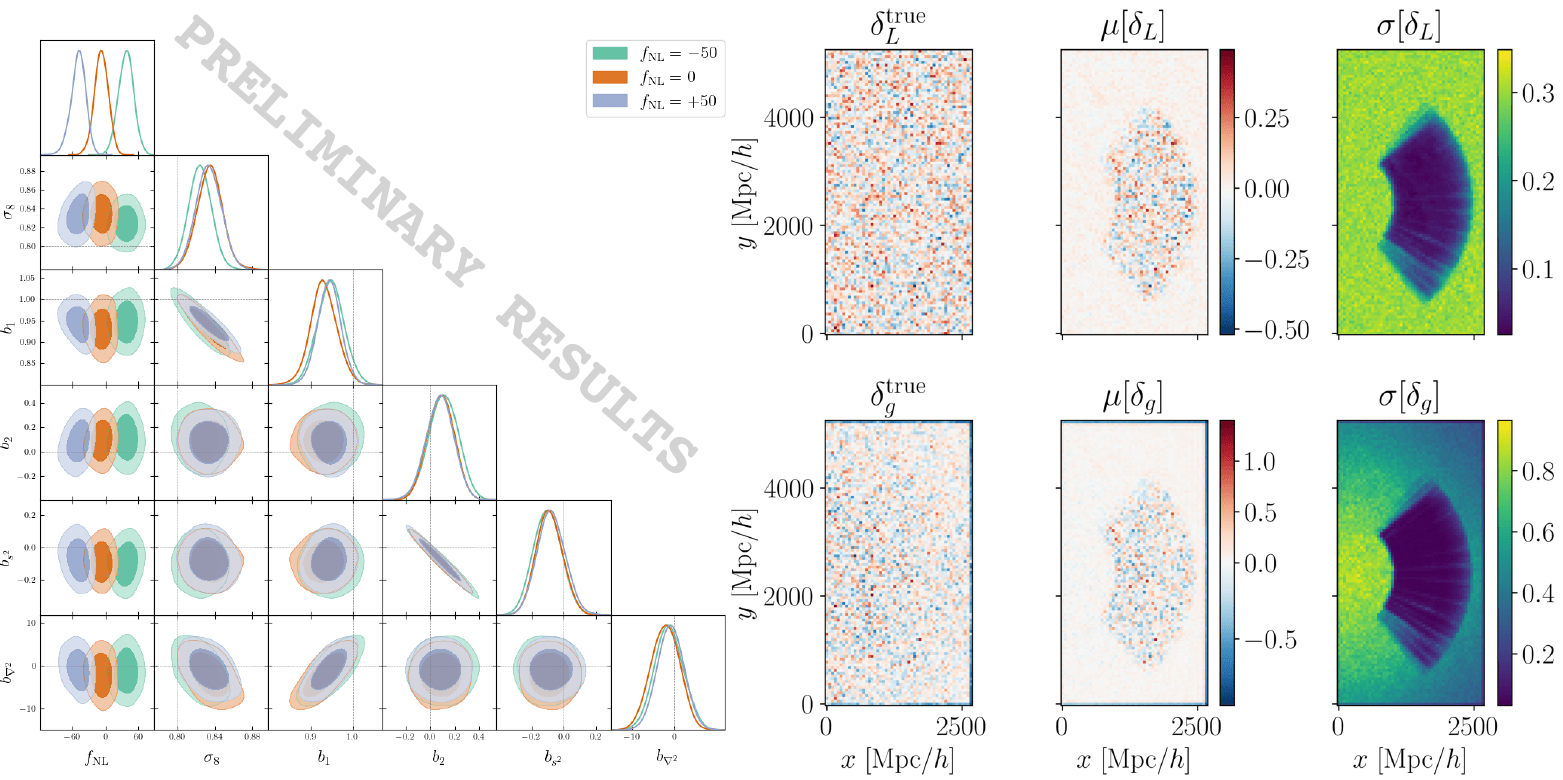
first checking:
- self-specified model
- N-body simulations
- observational systematics
Conclusions
- DESI data taking is running incredibly smoothly. Survey extended to 8 years, 63 M extra-galactic redshifts
- DESI delivered BAO results with DR2: hints of evolving dark energy?
- Full Shape analyses to constrain structure growth and modified gravity
- Including bispectrum (3-point correlation function)
- Personal interests:
- develop algorithms and GPU-accelerated codes to facilitate these standard analyses
- develop alternative "field-level inference" analysis
Back-up
Q&A
- Impact of Planck likelihood, update with ACT DR6
- Neutrino mass hierarchy / Effective neutrino mass
- Comment on Efstathiou+25
- BAO DR2/DR1 vs CMB tension?
- OK to combine with SN?
- Solutions to the BAO DR2/DR1 vs CMB "tension"?
- Optical depth \(\tau\)
- Early Dark Energy
Planck likelihoods
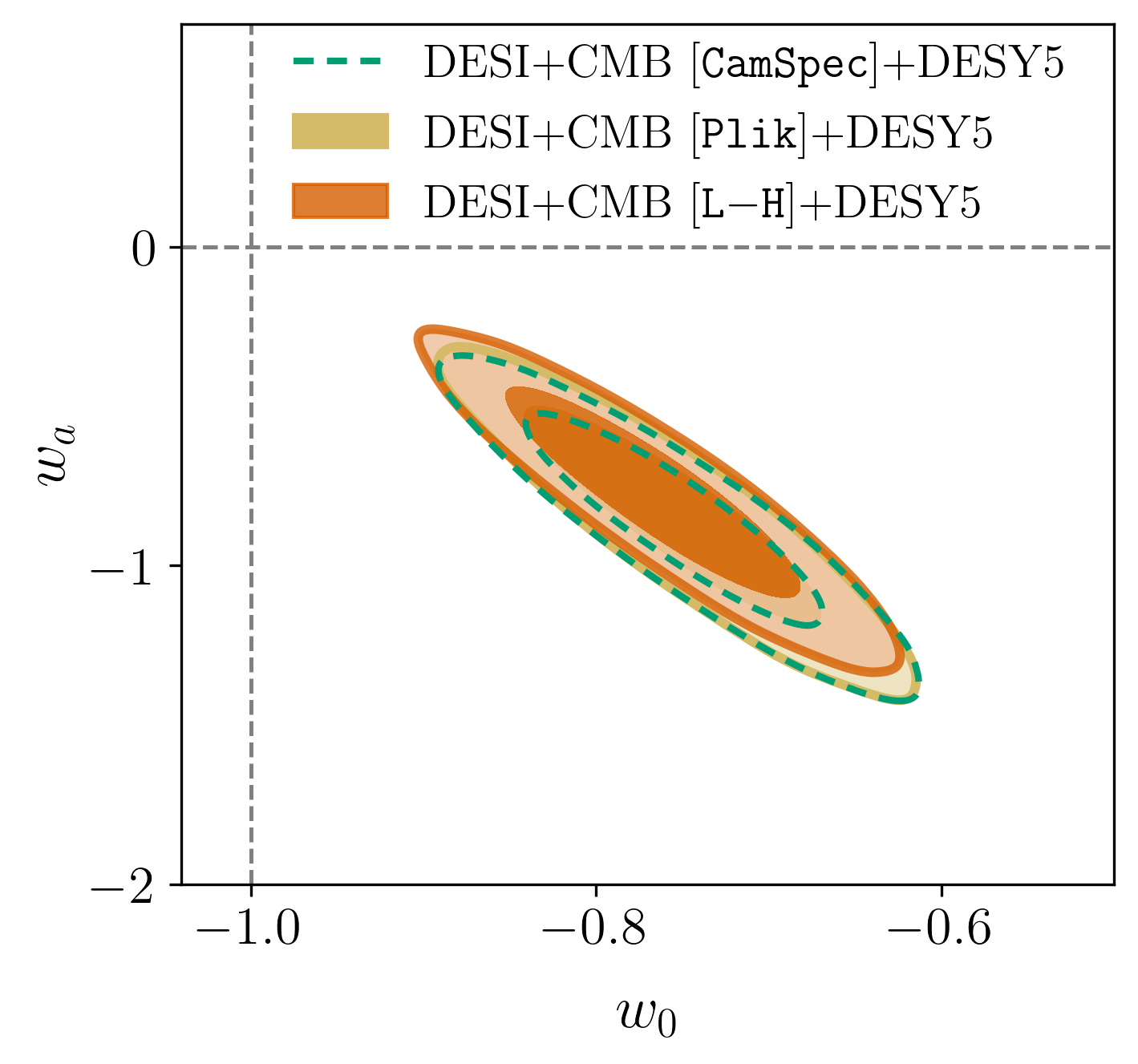
Preference for \(w_0w_a\mathrm{CDM}\) robust to various Planck likelihoods:
- CamSpec PR4 (baseline)
- Plik PR3
- LiLLiPoP-LolliPoP (PR4)
Planck likelihoods
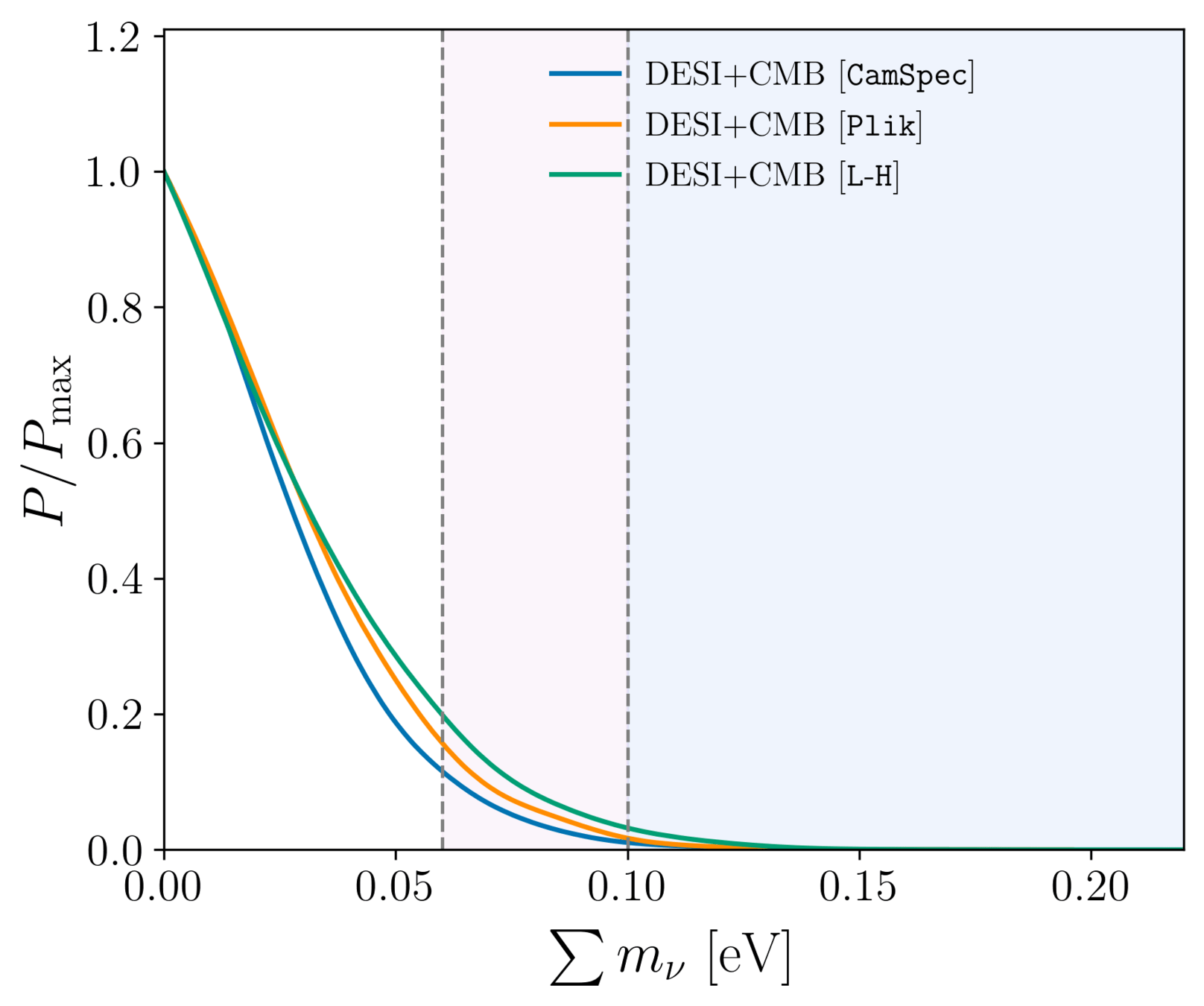
Upper limit on the sum of neutrinos masses depends on the choice of CMB likelihood. With DESI + CMB:
- \(\sum m_\nu < 0.064 \, \mathrm{eV} \; (95\%, \text{CamSpec PR4})\)
- \(\sum m_\nu < 0.069 \, \mathrm{eV} \; (95\%, \text{Plik PR3})\)
- \(\sum m_\nu < 0.077 \, \mathrm{eV} \; (95\%, \text{L-H})\)
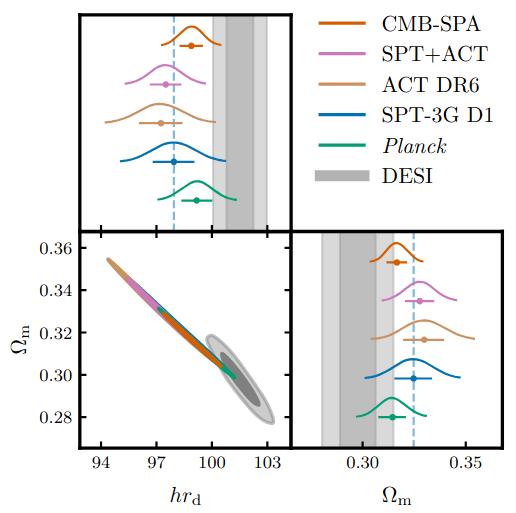
Combining with ACT DR6
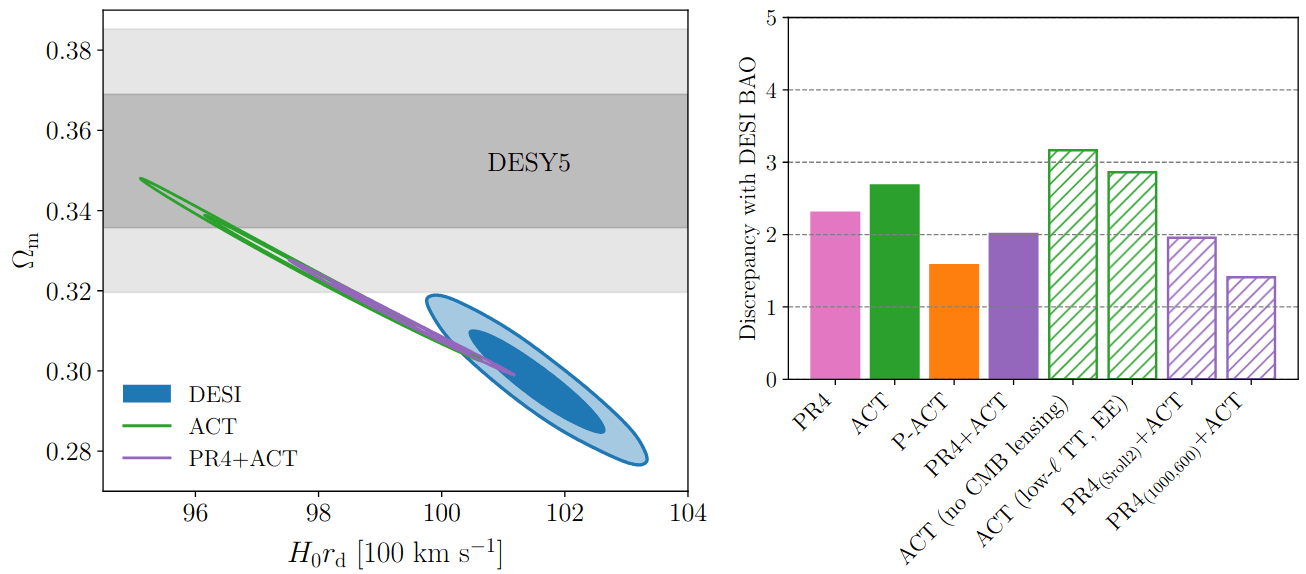
ACT released DR6 CMB measurements and cosmological constraints the day before DESI
Discrepancy with DESI:
- PR4: \(2.3\sigma\)
- ACT DR6: \(2.7\sigma\)
- PR4+ACT: "best" CMB constraints with PR4 on \(\ell < 2000 \) TT, \(< 1000\) TE, EE: \(2.0 \sigma\)
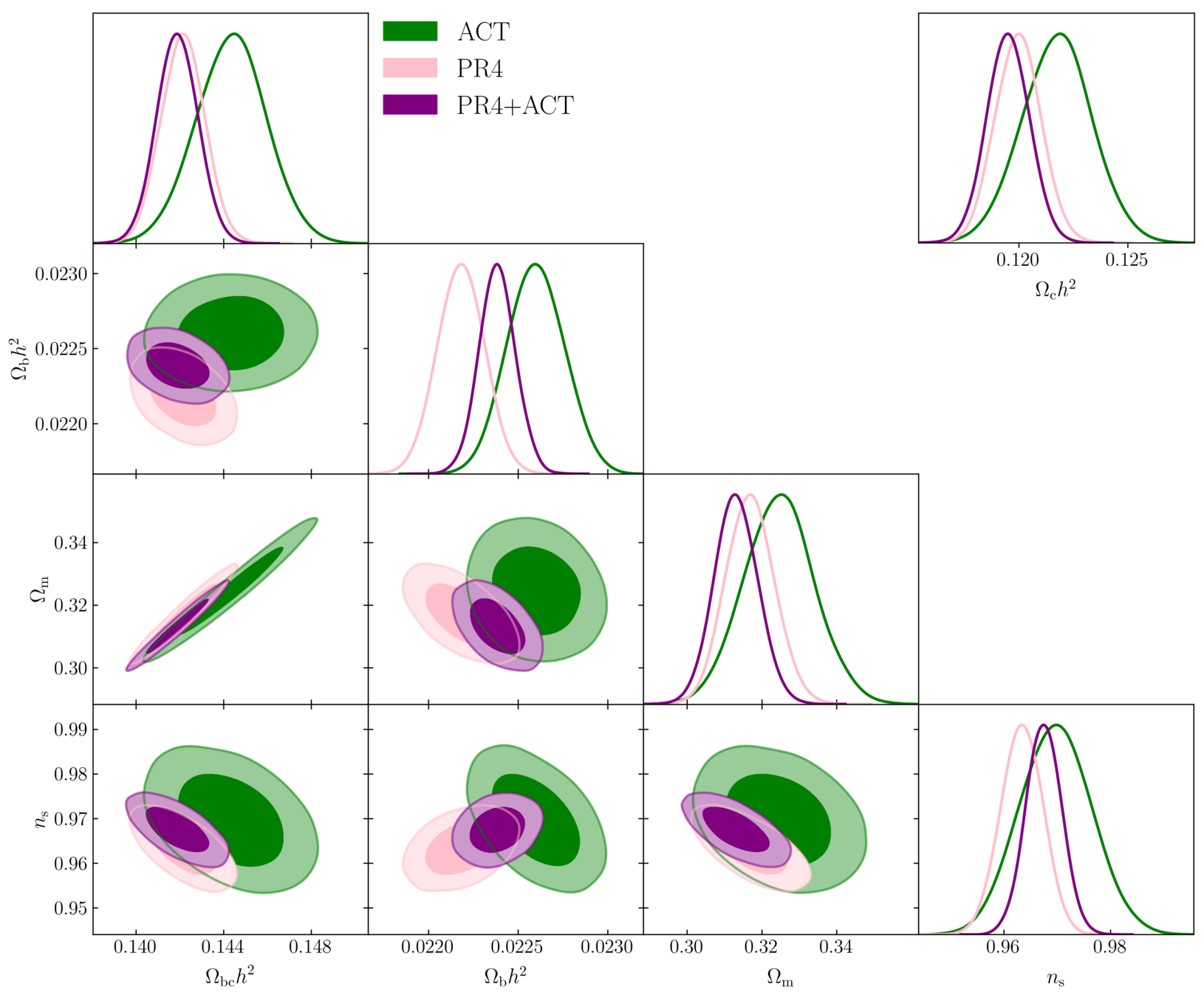
higher \(\Omega_\mathrm{m}\)
higher \(\Omega_\mathrm{bc}h^2, \Omega_\mathrm{b}h^2\)
\(\Omega_\mathrm{b}h^2\) in-between
different degeneracy directions
lower \(\Omega_\mathrm{bc}h^2, \Omega_\mathrm{m}\)
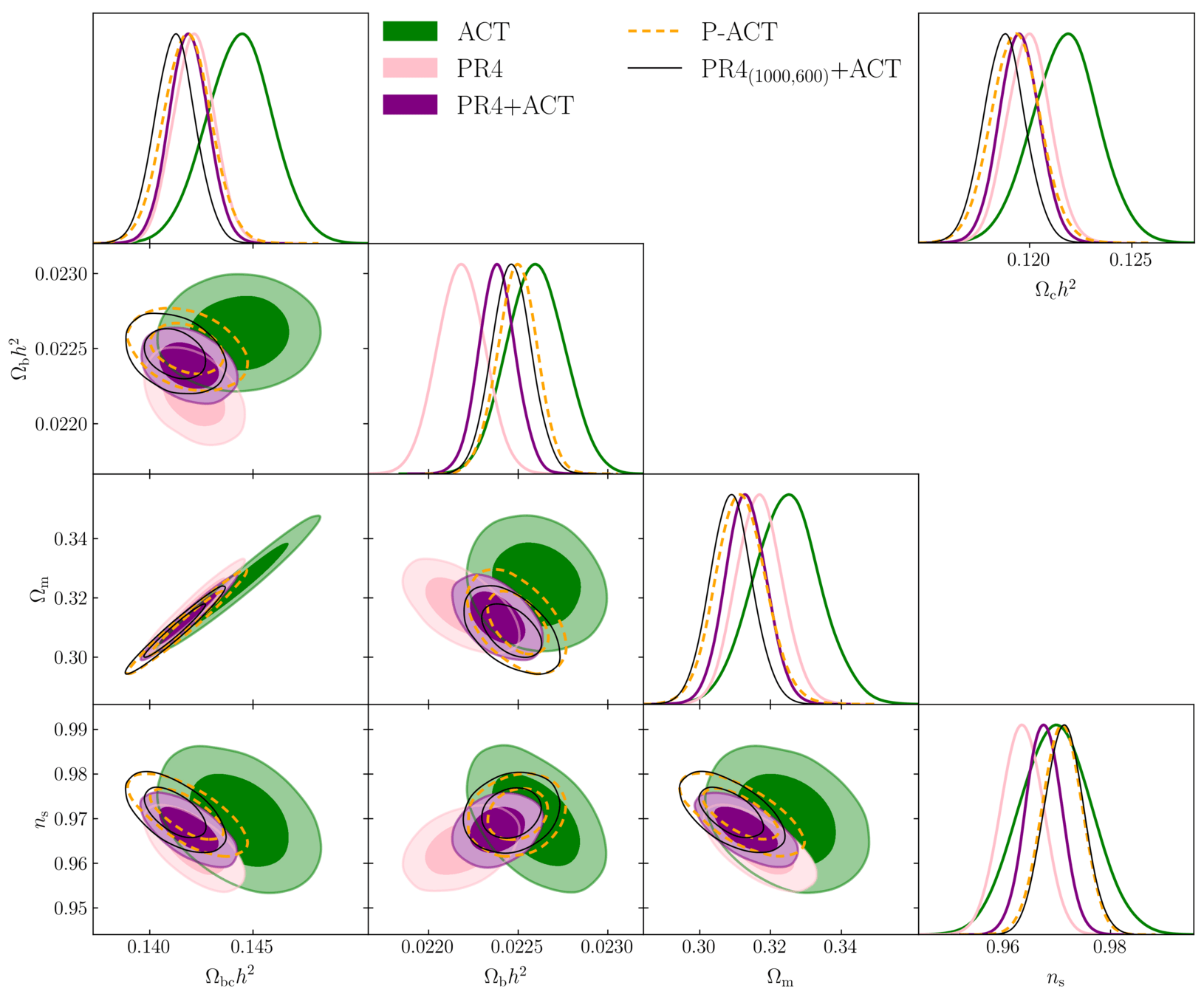
PR4+ACT with same \(\ell\) cuts as P-ACT: increases ACT weight
\(\Rightarrow\) consistent with P-ACT
Combining with ACT DR6
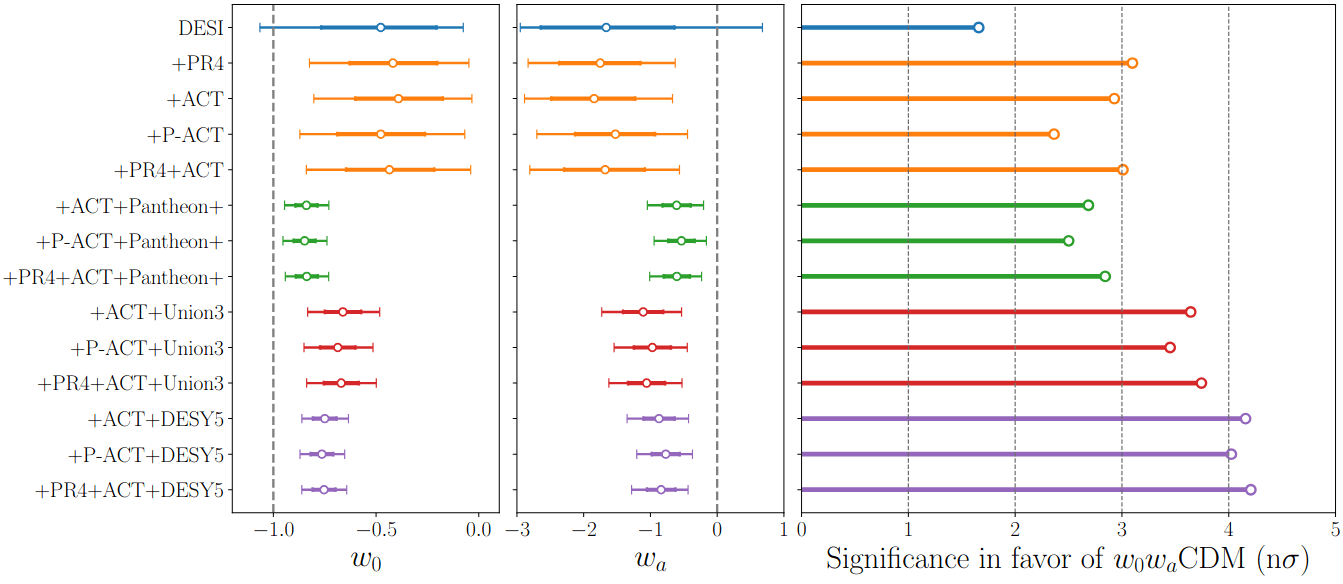
When including SN, reference for \(w_0w_a\mathrm{CDM}\) is stable w.r.t. CMB dataset
Combining with ACT DR6
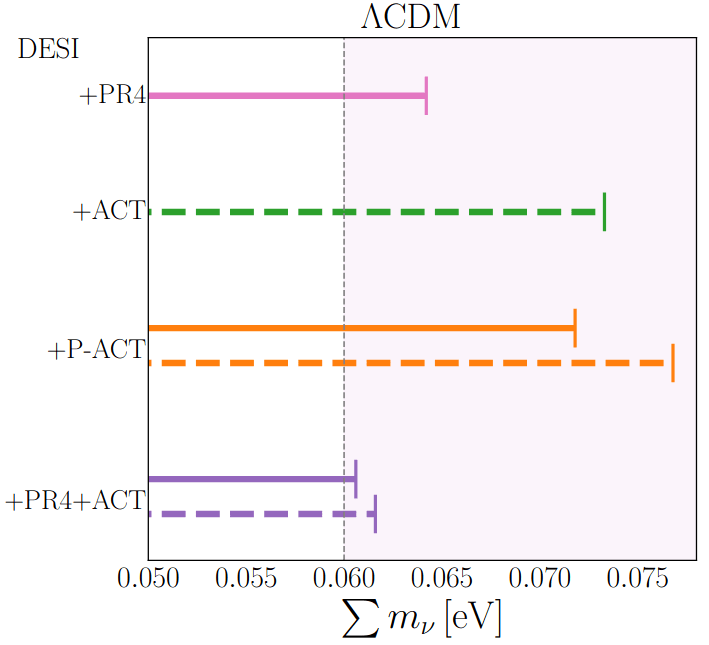
Limit at \(95\%\) on \(\sum m_\nu\):
DESI+PR4: \(< 0.064\,\mathrm{eV}\)
DESI+ACT: \(< 0.073\,\mathrm{eV}\)
DESI+P-ACT: \(< 0.077\,\mathrm{eV}\)
PR4+ACT: \(< 0.061\,\mathrm{eV}\)
low-\(\ell\) Sroll2 EE likelihood (instead of SimAll)
Calabrese+25 with DESI DR1: \(<0.83\,\mathrm{eV}\)
Sum of neutrino masses
Neutrino mass oscillations constrain \(\Delta m_{21}^2\) and \(\vert \Delta m_{31}^2\vert\)
\(\sum m_\nu = m_1 + \sqrt{m_1^2 + \Delta m_{21}^2} + \sqrt{m_1^2 + \Delta m_{31}^2}\)
\(m_3 + \sqrt{m_3^2 - \Delta m_{31}^2} + \sqrt{m_3^2 + \Delta m_{32}^2}\)
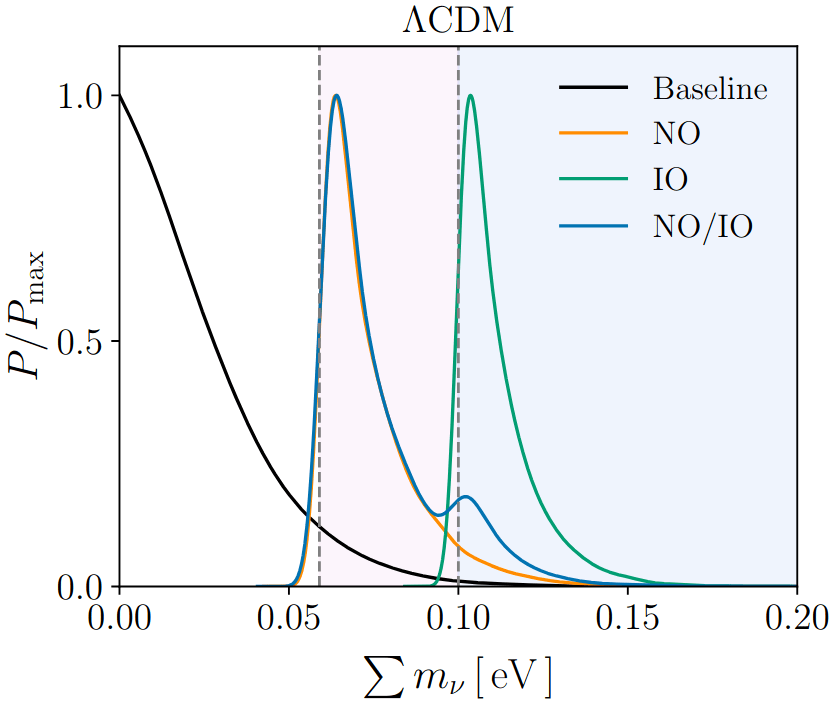
prior NO/IO: 0.5/0.5
\sum m_\nu < 0.101 \, \mathrm{eV} \; (95\%, \text{NO})
\sum m_\nu < 0.133 \, \mathrm{eV} \; (95\%, \text{IO})
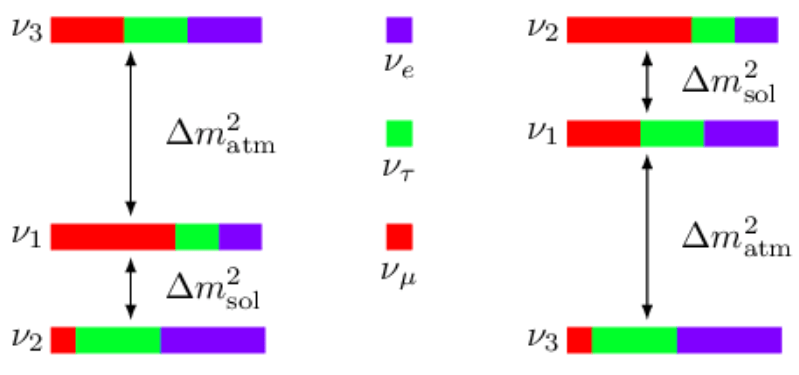
Normal Ordering (NO)
Inverted Ordering (IO)
\Rightarrow P(\mathrm{NO}) = 1 - P(\mathrm{IO}) = 0.91
Sum of neutrino masses
Limit relaxed for \(w_0w_a\mathrm{CDM}\):
DESI+CMB: \(\sum m_\nu < 0.163 \, \mathrm{eV} \; (95\%)\)
DESI+CMB+DESY5: \(< 0.129 \, \mathrm{eV} \; (95\%)\)
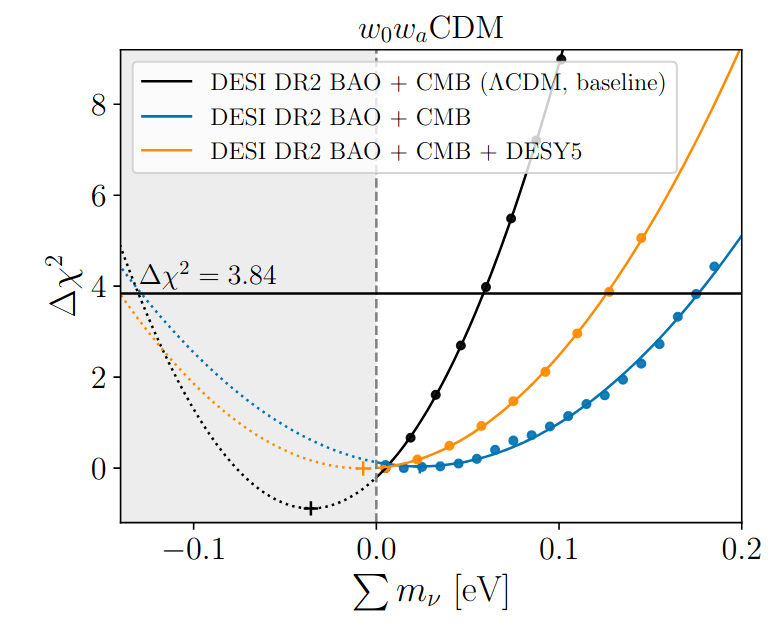
\(w_0w_a\) shifts to positive \(\sum m_\nu\)
profile likelihood
adding SN shifts the minimum back towards negative \(\sum m_\nu\)
Effective neutrino mass
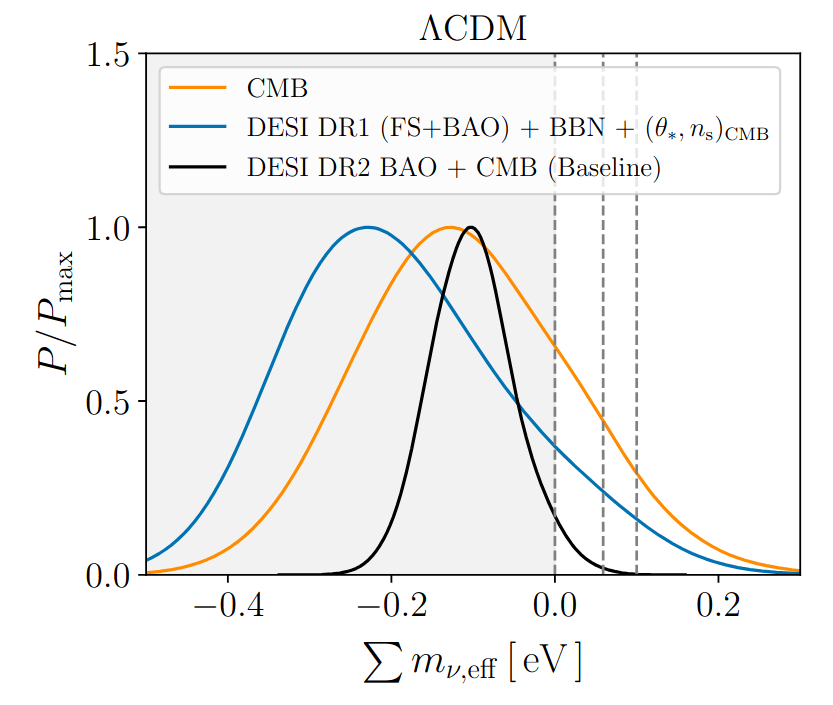
Effective neutrino mass \(\sum m_{\nu, \mathrm{eff}}\) that can be extended to negative values (through negative energy density)
DESI+CMB:
\(\sum m_{\nu, \mathrm{eff}} = -0.101_{-0.056}^{+0.047} \, \mathrm{eV} \; (68\%)\)
\(\sum m_{\nu} > 0.059\,\mathrm{eV}\) disfavored at \(3\sigma\)
Effective neutrino mass
\(\sum m_{\nu, \mathrm{eff}} = -0.11_{-0.14}^{+0.12} \, \mathrm{eV}\) preferred by the CMB alone
Effective neutrino mass
\(\sum m_{\nu, \mathrm{eff}} < 0\) weakens the preference for \(w_0w_a\mathrm{CDM}\) (only when inc. CMB)
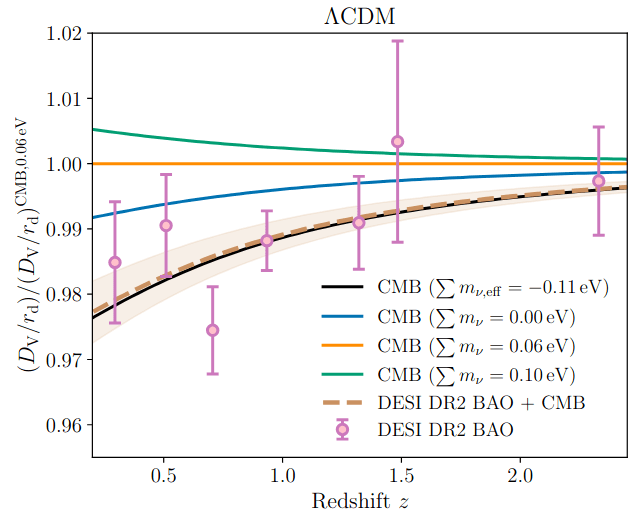
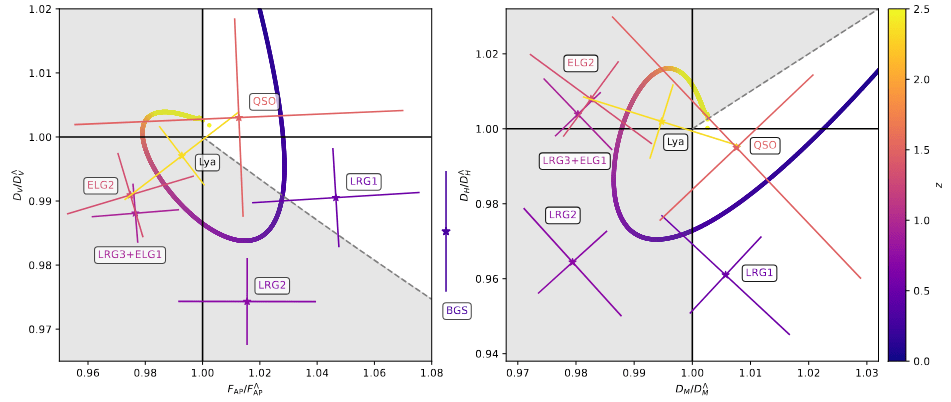
DESI DR2 / DR1 vs Planck
\(\mathcal{D}_\parallel, \mathcal{D}_\perp = \mathrm{Rot}(D_\mathrm{H}/r_\mathrm{d}, D_\mathrm{M}/r_\mathrm{d})\) with \(\mathcal{D}_\perp\) best constrained by Planck
following Efstathiou+25
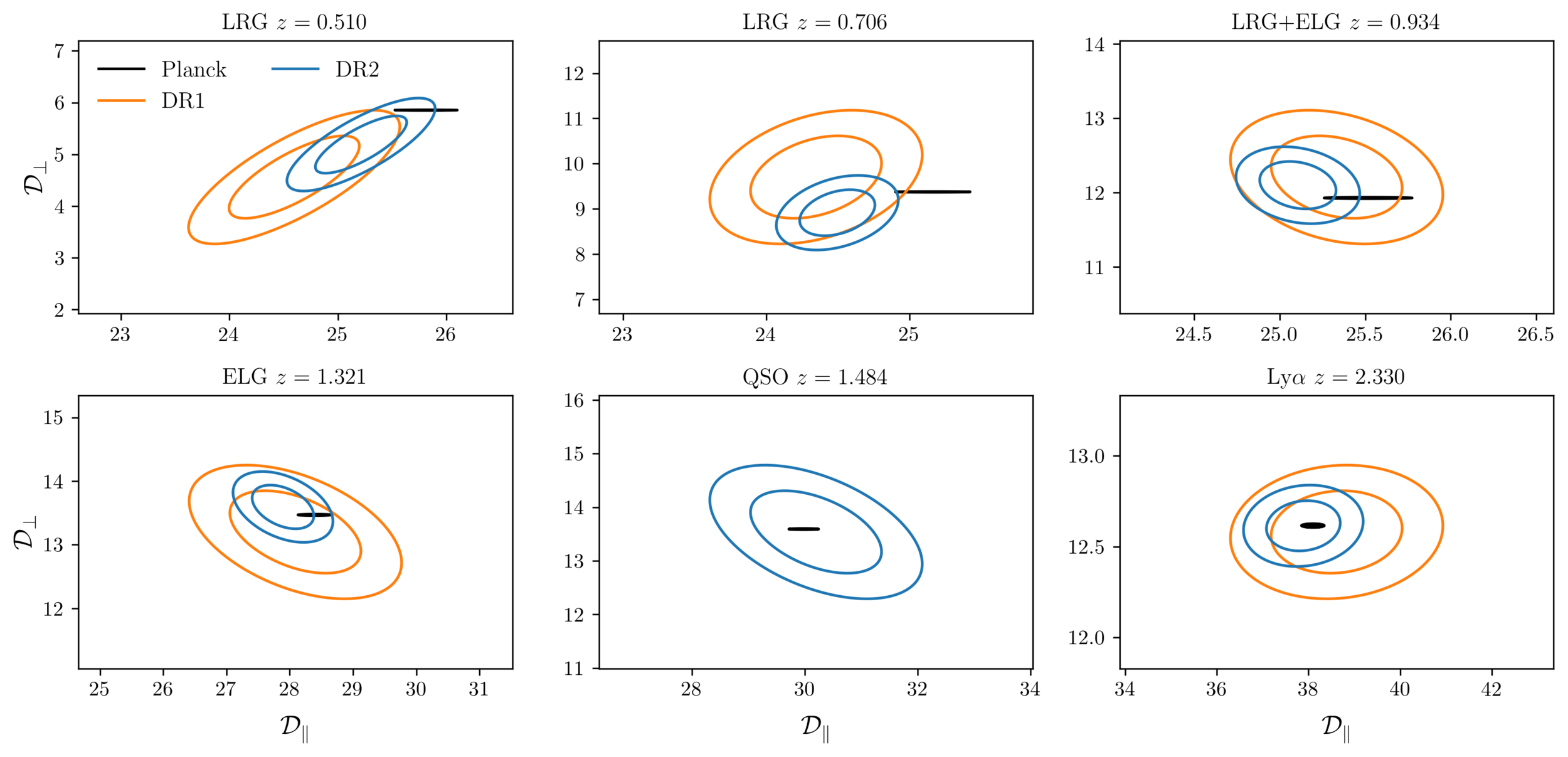
DESI DR2 / DR1 vs Planck
following Efstathiou+25
turned into \(\omega_\mathrm{bc}\) constraint
DR2 more consistent
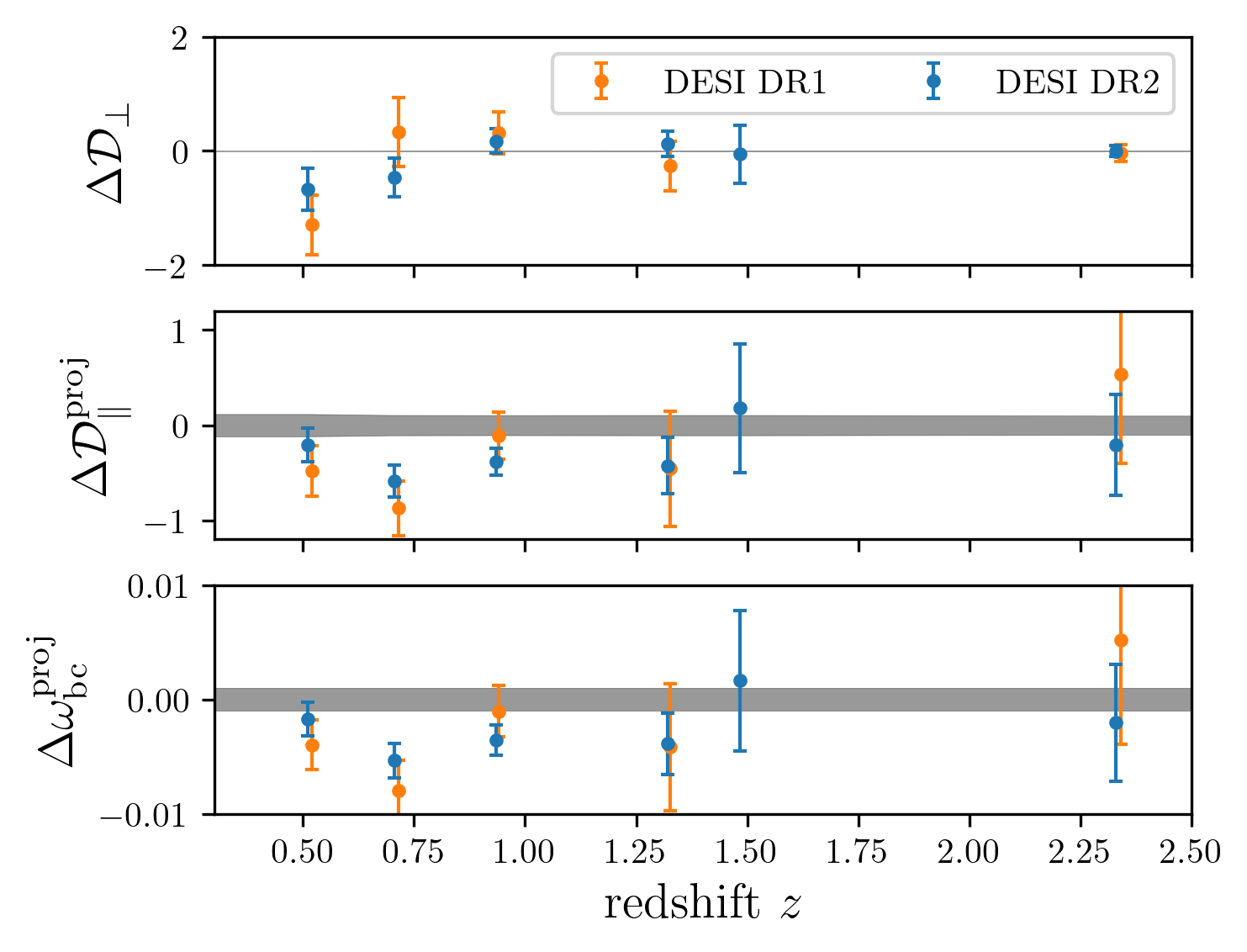
DESI DR2 / DR1 vs Planck
\(\omega_\mathrm{m}\)
- \(2.3 \sigma\) discrepancy with primary CMB + CMB lensing
DESI DR2 / DR1 vs Planck
following Efstathiou+25
With CMB = low-\(\ell\) PR3 + CamSpec PR4 + (ACT+PR4) lensing
\(H_0r_d, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(2.3\sigma\)
\(2.2\sigma\)
\(2.2\sigma\)
\(1.8\sigma\)
\(1.9\sigma\)
\(2.1\sigma\)
\(0.8\sigma\)
\(2.6\sigma\)
\(2.7\sigma\)
\(1.3\sigma\)
\(2.1\sigma\)
\(2.3\sigma\)
no isotropic BAO
following Efstathiou+25
\(\mathcal{D}_\perp, \mathcal{D}_\parallel\) space
\(2.2\sigma\)
\(2.1\sigma\)
rotation
multiple counting of Planck uncertainty
DESI DR2 / DR1 vs Planck
following Efstathiou+25
\(H_0r_d, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(1.9\sigma\)
\(1.9\sigma\)
\(1.9\sigma\)
\(1.6\sigma\)
\(1.7\sigma\)
\(2.0\sigma\)
\(0.8\sigma\)
\(2.2\sigma\)
\(2.3\sigma\)
\(1.3\sigma\)
\(1.9\sigma\)
\(2.1\sigma\)
no isotropic BAO
\(\mathcal{D}_\perp, \mathcal{D}_\parallel\) space
\(1.9\sigma\)
\(2.0\sigma\)
With CMB = low-\(\ell\) PR3 + CamSpec PR4
Combining with DESY5 SN?
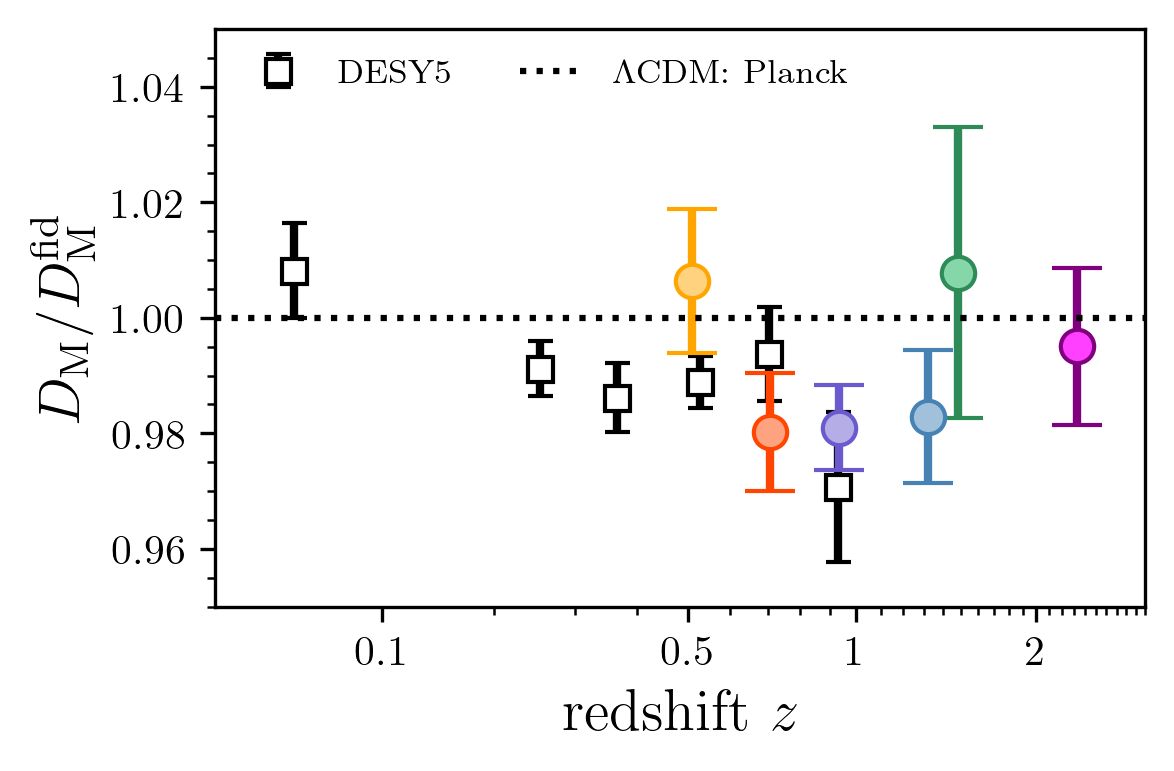
agreement between DESI BAO and DESY5 data at \(\sim 1.5\sigma\) level
\Lambda\mathrm{CDM}
In the overlapping \(z\)-range, DESI DR2 BAO and DESY5 SN agree
\(\simeq 0.9 \sigma\)
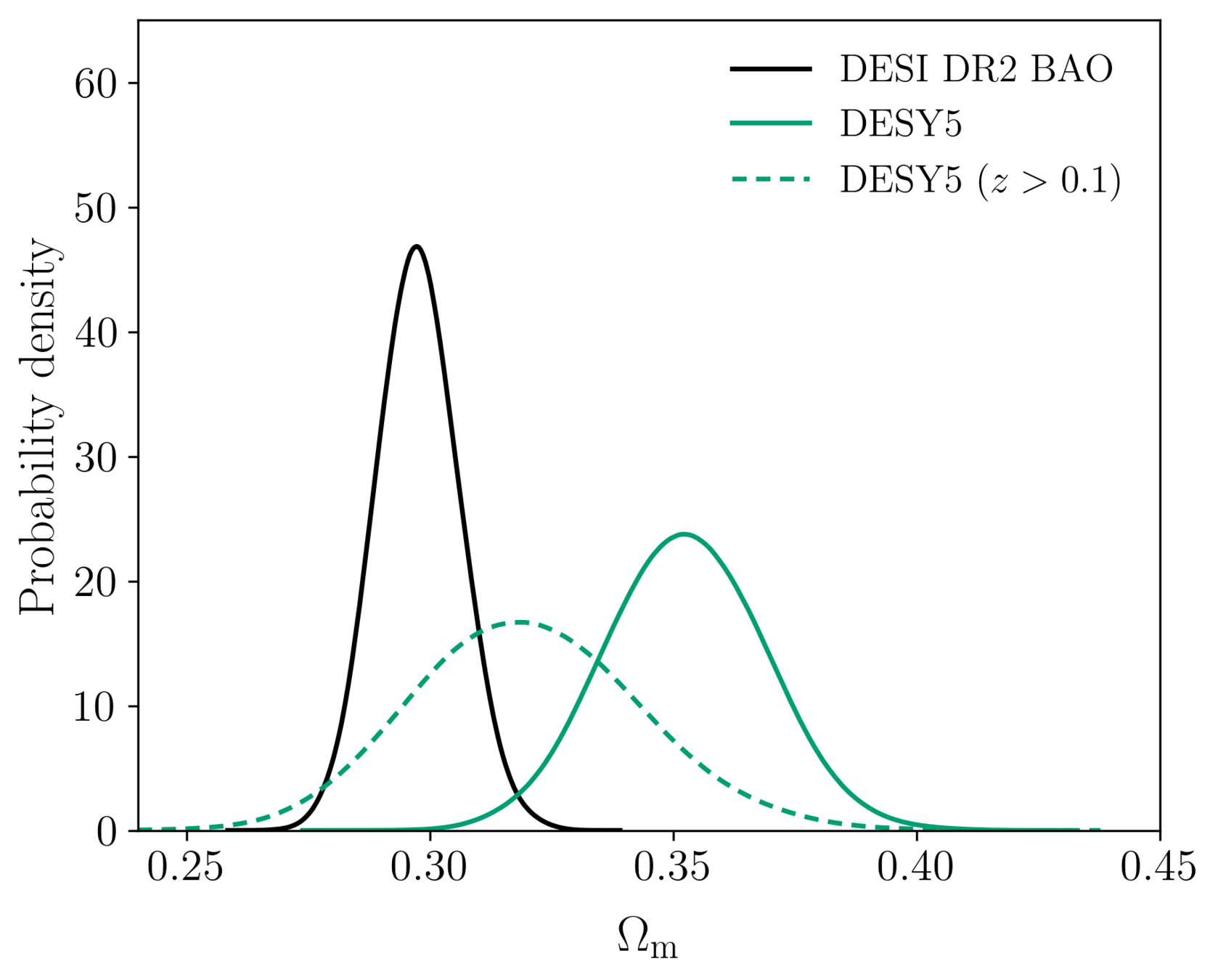
Combining with DESY5 SN?
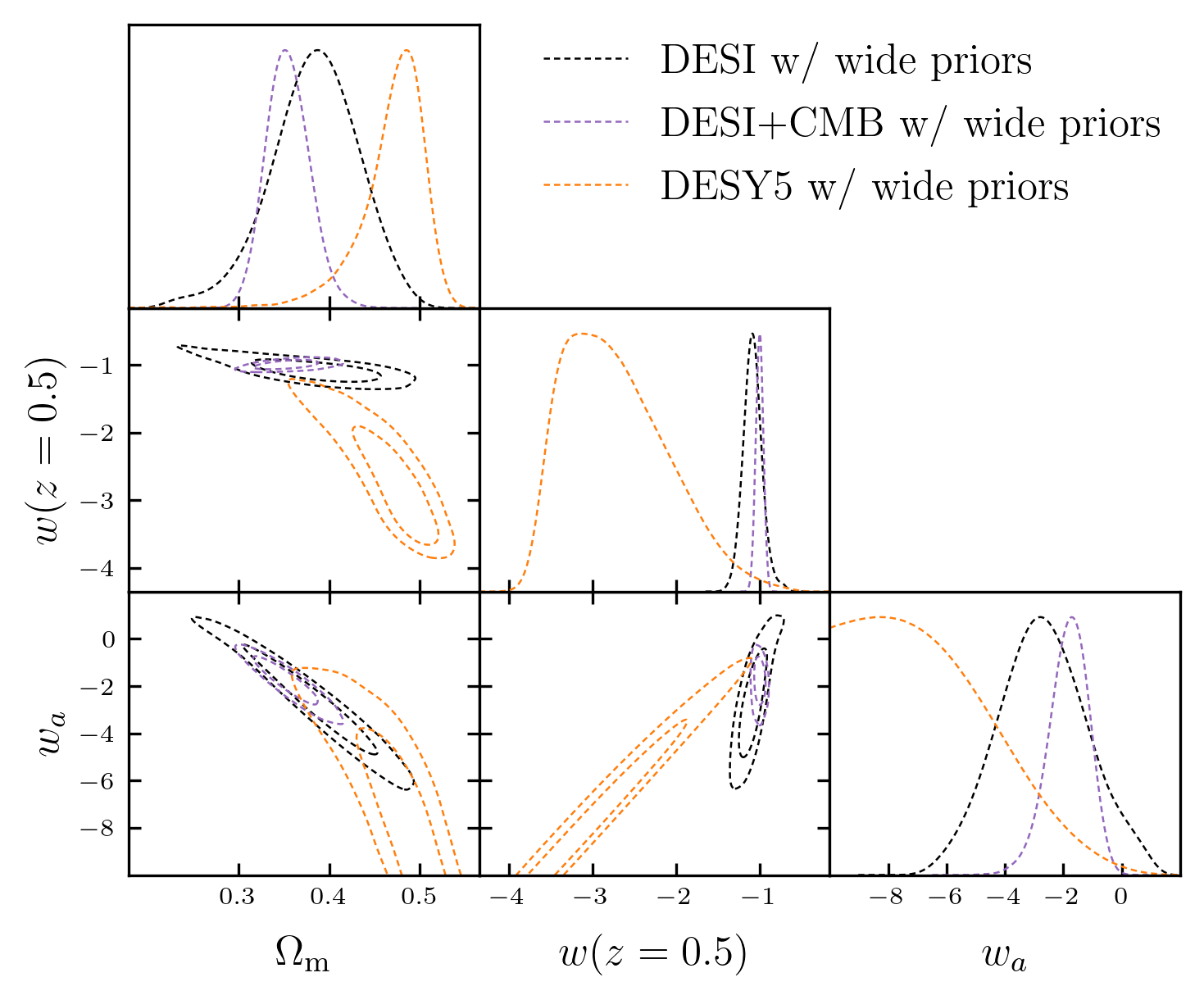
Combining with DESY5 SN?
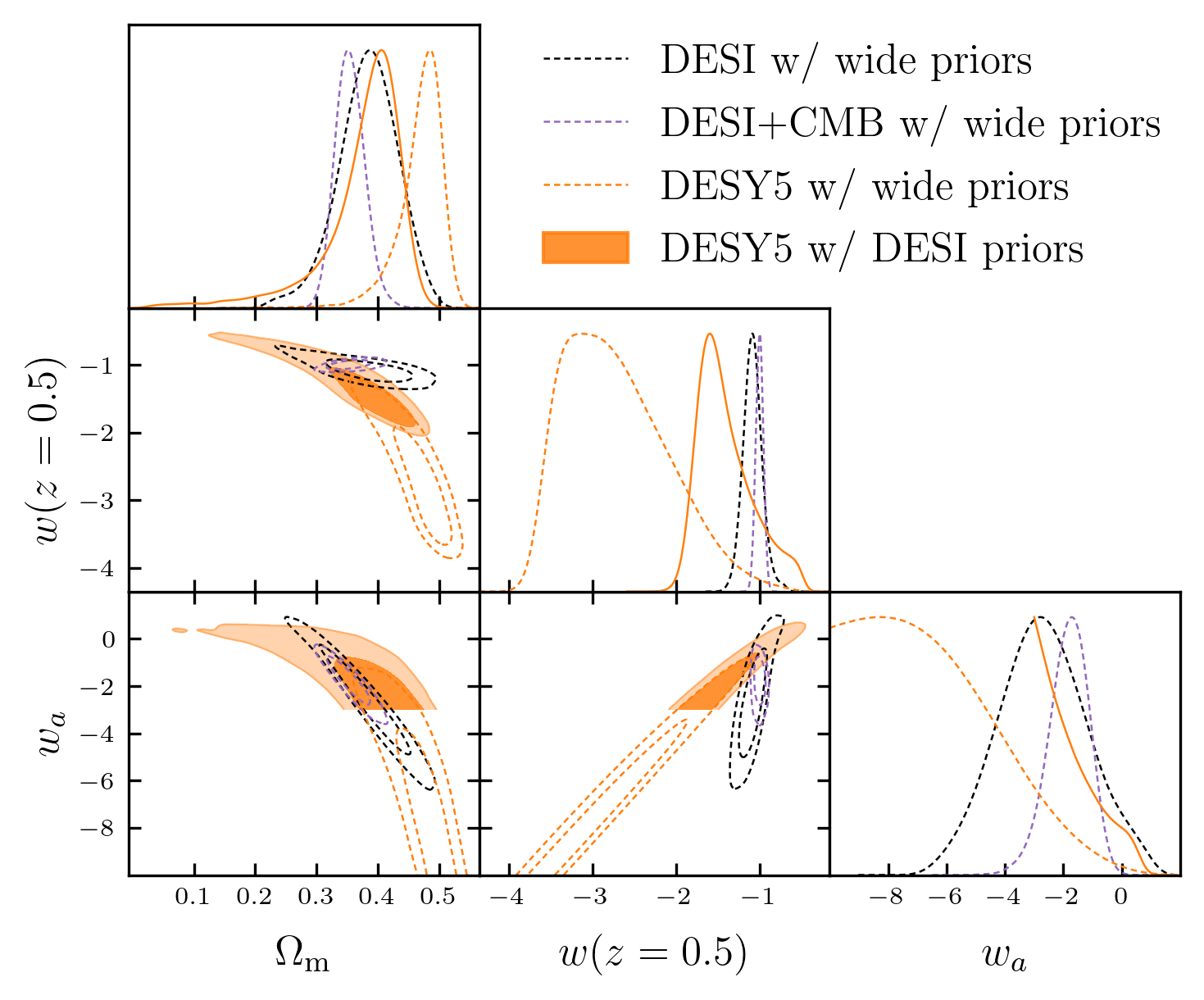
Combining with DESY5 SN?
\(\Delta \chi^2 \simeq 5.5\)
\(\chi^2_\mathrm{min} \simeq 1632, \mathrm{ndof} = 1829\)
Combining with DESY5 SN?
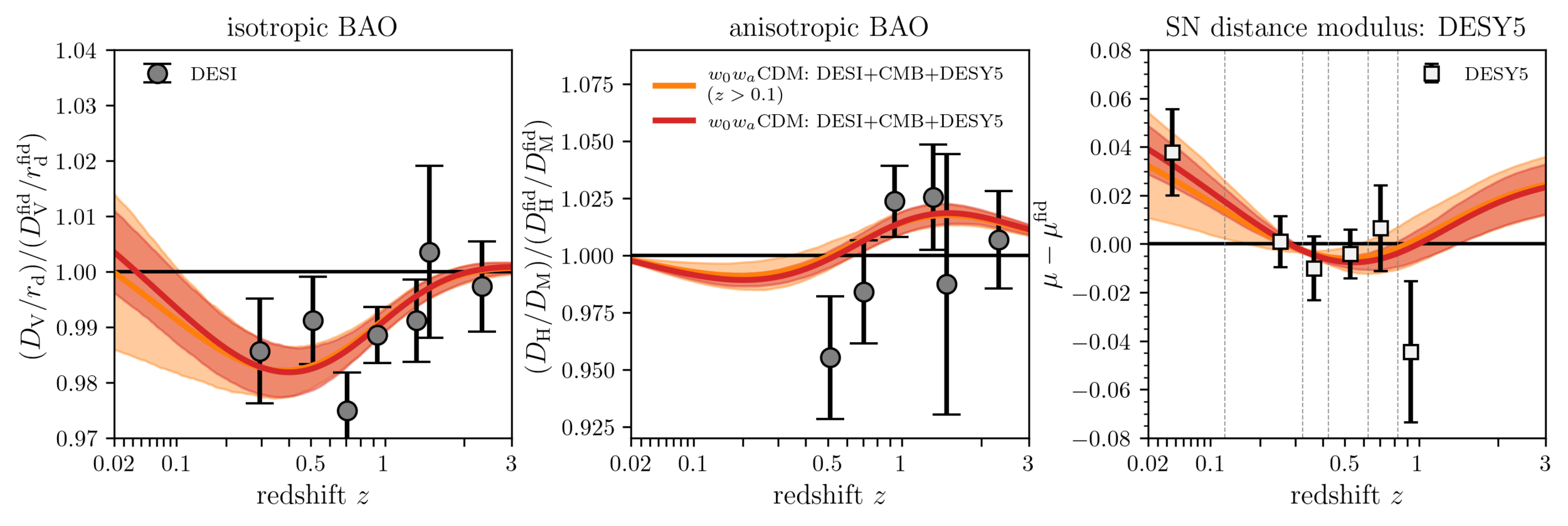
assuming \(z > 0.1\) fit, including the \(z < 0.1\) SN data
\(\Rightarrow\) \(\Delta \chi^2 = 186, \mathrm{ndof} = 197\)
full DESY5 best \(\chi^2\) barely changes between \(z > 0.1\) and full fit
Combining with DESY5 SN?
assuming \(z > 0.1\) fit, including the \(z < 0.1\) SN data
\(\Rightarrow\) \(\Delta \chi^2 = 186, \mathrm{ndof} = 197\)
full DESY5 best \(\chi^2\) barely changes between \(z > 0.1\) and full fit
Optical depth \(\tau\)
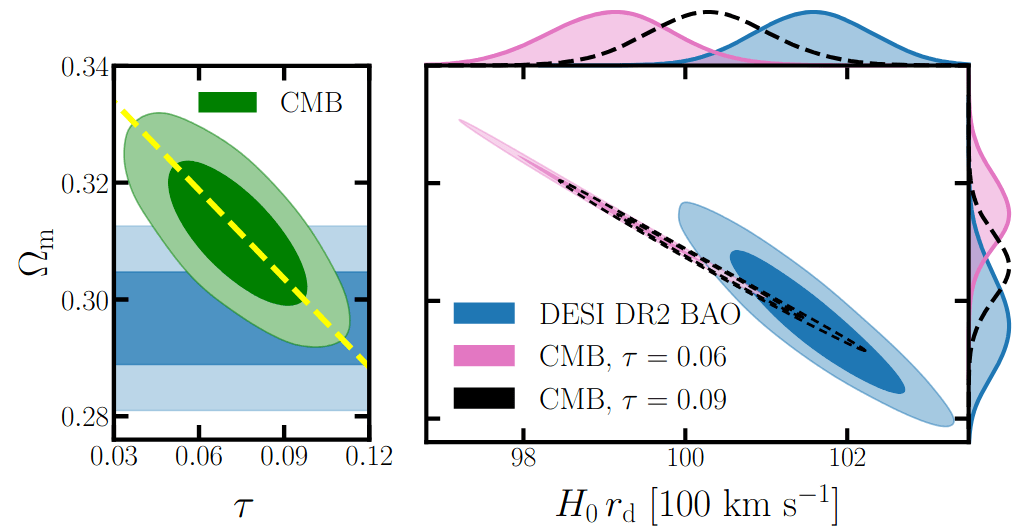
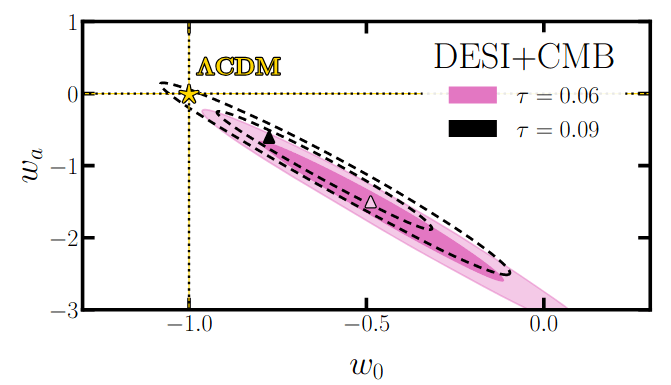
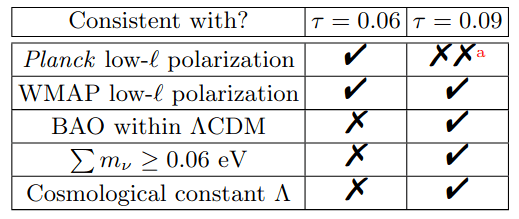
\(\tau = 0.09\) \(3\sigma \Rightarrow 1.5\sigma\) for \(w_0w_a\mathrm{CDM}\)
3-5\(\sigma\) tension in low-\(\ell\) Planck polarization
Strengthens the case for future CMB experiments
\(3\sigma \Rightarrow 1.5\sigma\)
Early Dark Energy
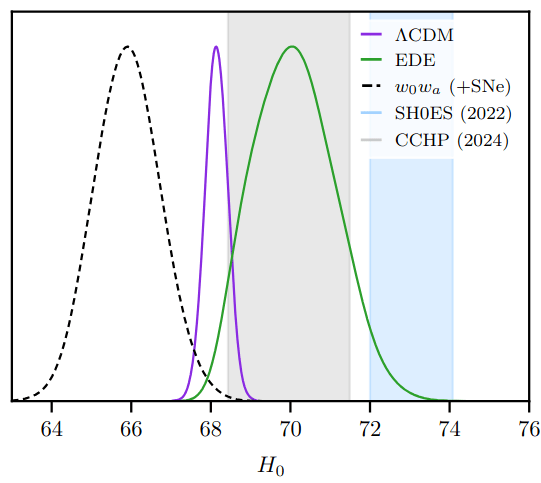
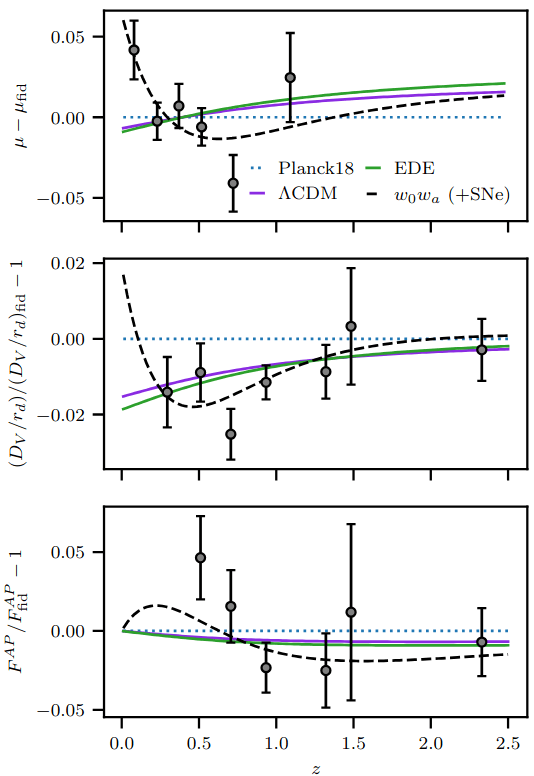
- Minimally-coupled scalar field for an early-type modification of the expansion history (changes \(r_\mathrm{d}\))
- Solves tension with local Hubble measurements, but less favored with SN
| CMB+BAO | ||
| +Union3SN |
EDE
\(w_0w_a\)
-7.4
-7.5
-12.5
-17.4
\(\Delta \chi^2\) / \(\Lambda\mathrm{CDM}\)
Dark Energy Evolution
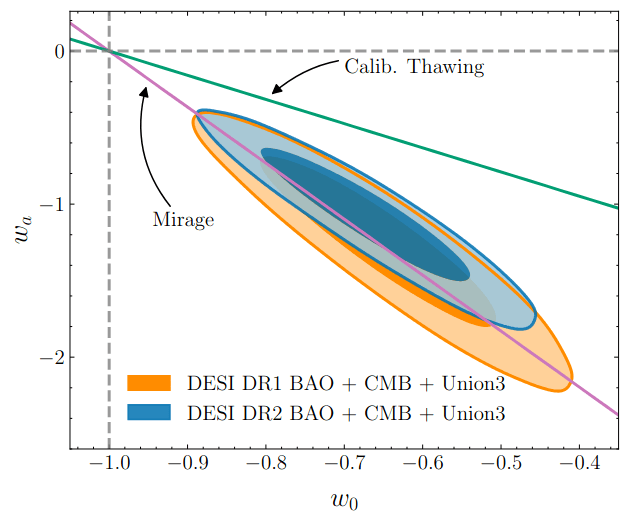
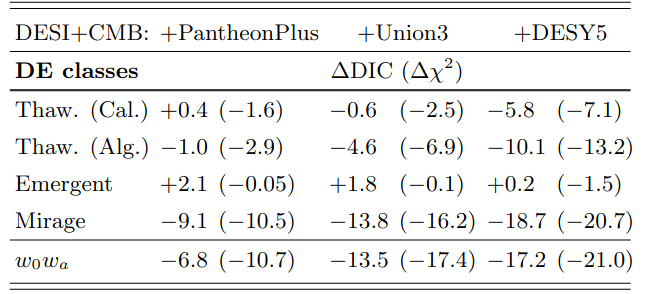
no phantom crossing
Dark Energy Evolution
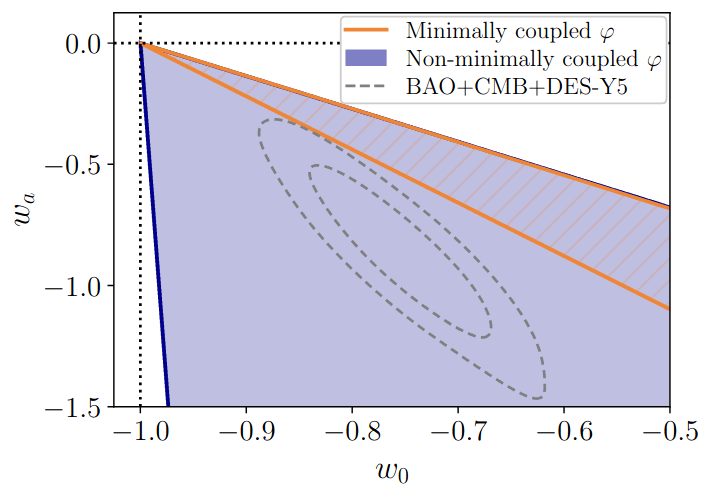
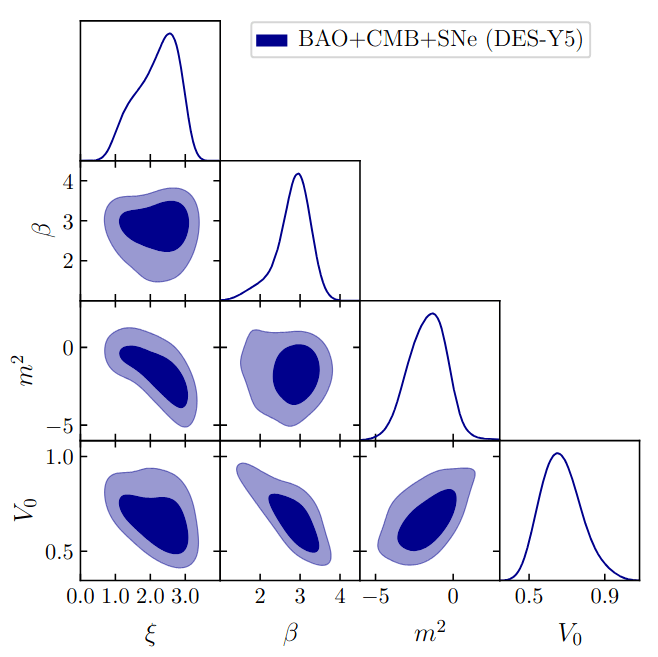
coupling
\(m² < 0\): hilltop
Dark Energy Evolution
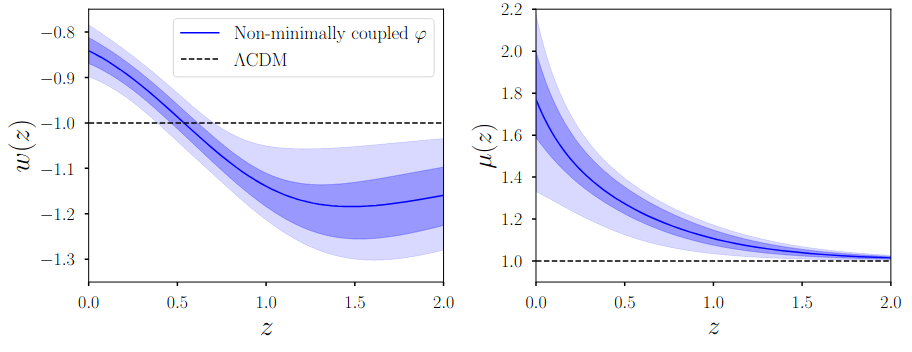
MG
But adds a fifth force, inconsistent with solar system constraints
Coupling between DE/DM instead? But see Linder+25
Other datasets
- SDSS BAO (for comparisons only): eBOSS Collaboration, 2020
- Primary CMB: CamSpec PR4, HiLLiPoP/LoLLiPoP, Planck Collaboration, 2018
- CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
- BBN: Schöneberg et al., 2024
- SN: Pantheon+ Brout, Scolnic, Popovic et al., 2022, Union3 Rubin, Aldering, Betoule et al. 2023, DES-SN5YR DES Collaboration
Analysis pipeline mostly the same as DR1
Again, blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
Anisotropic BAO measurements for QSO (and low-\(z\) ELG)
Minor updates:
- revised min fitting range (\(60 < s / [\mathrm{Mpc}/h] < 150\))
- revised systematic budget (theory, fiducial cosmology, HOD): \(\sigma_\mathrm{stat+syst} < 1.09 \sigma_\mathrm{stat}\)
Many more robustness tests
What's new in the BAO analysis?
BAO reconstruction
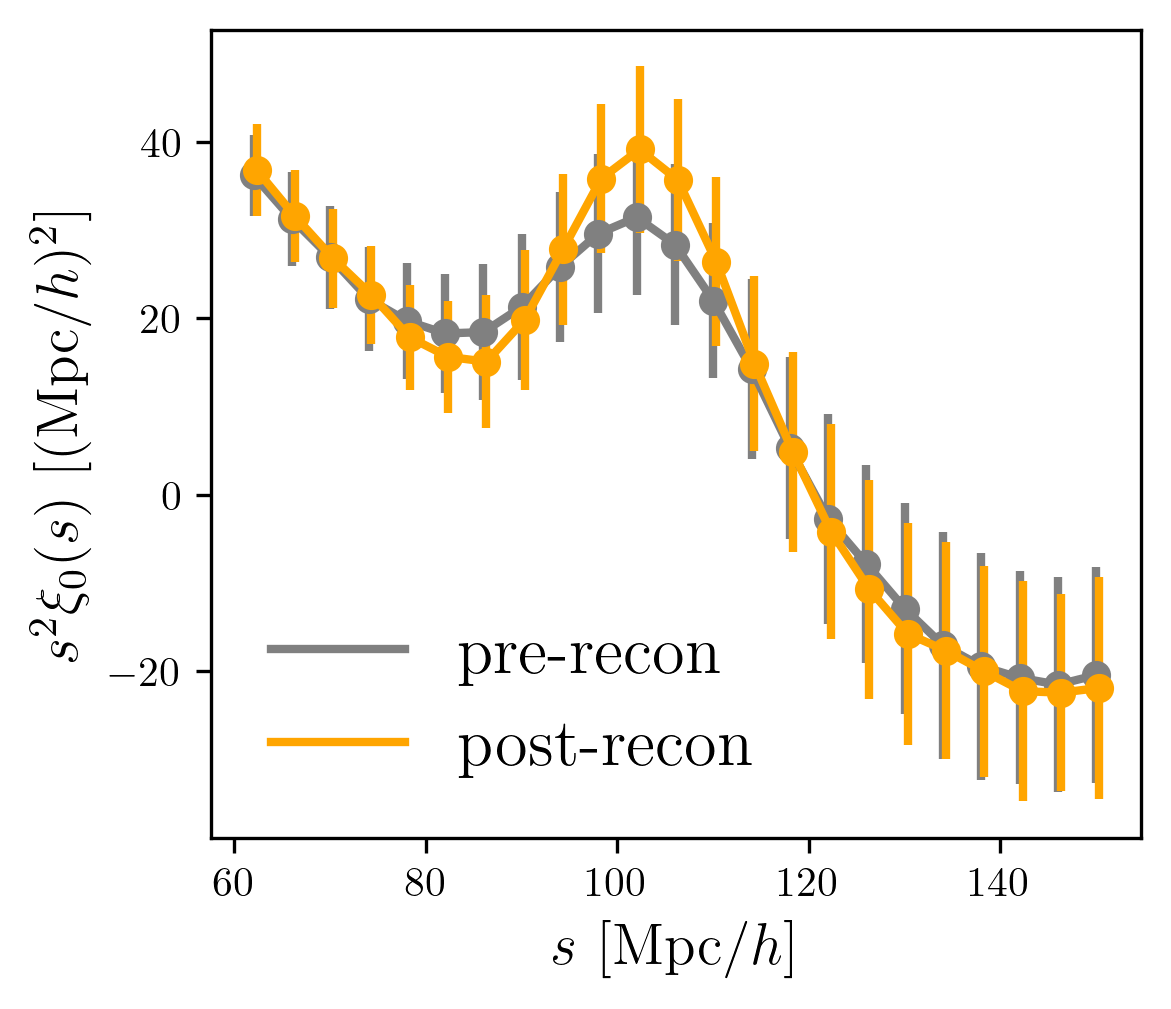
- Non-linear structure growth and peculiar velocities smear (and slightly displace) the BAO peak
- Reconstruction: estimate Zeldovich displacements from observed field and move galaxies back \(\rightarrow\) refurbishes the ruler (improves precision and accuracy)
Analysis pipeline mostly the same as DR1
Again, blind analysis to mitigate observer / confirmation biases (data vector-level blinding)
Improved modelling of metals and continuum-fitting distortions
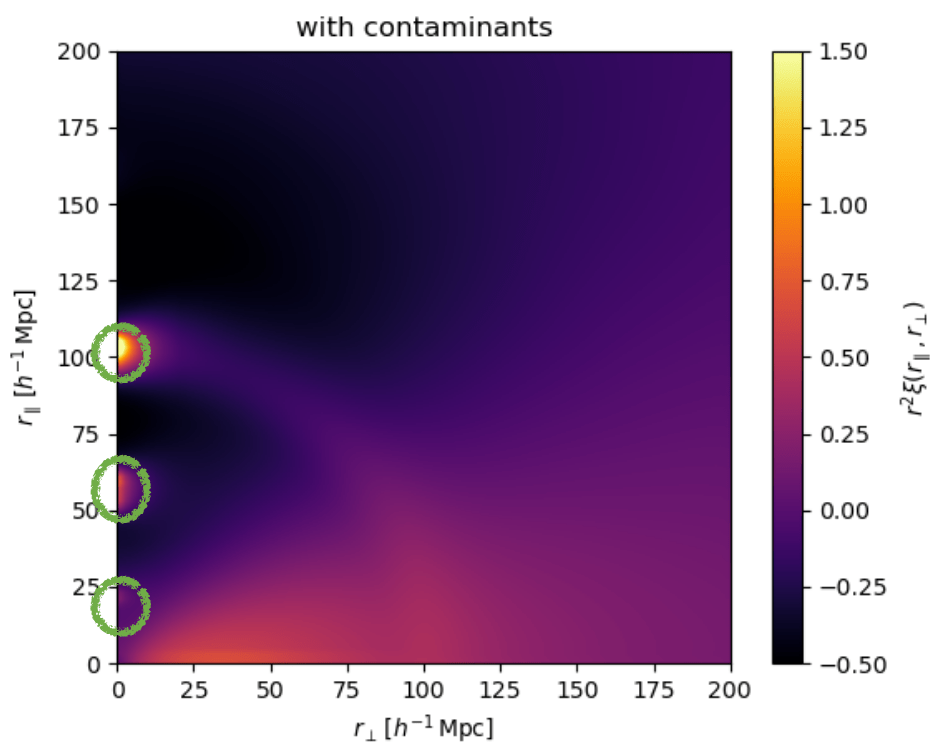
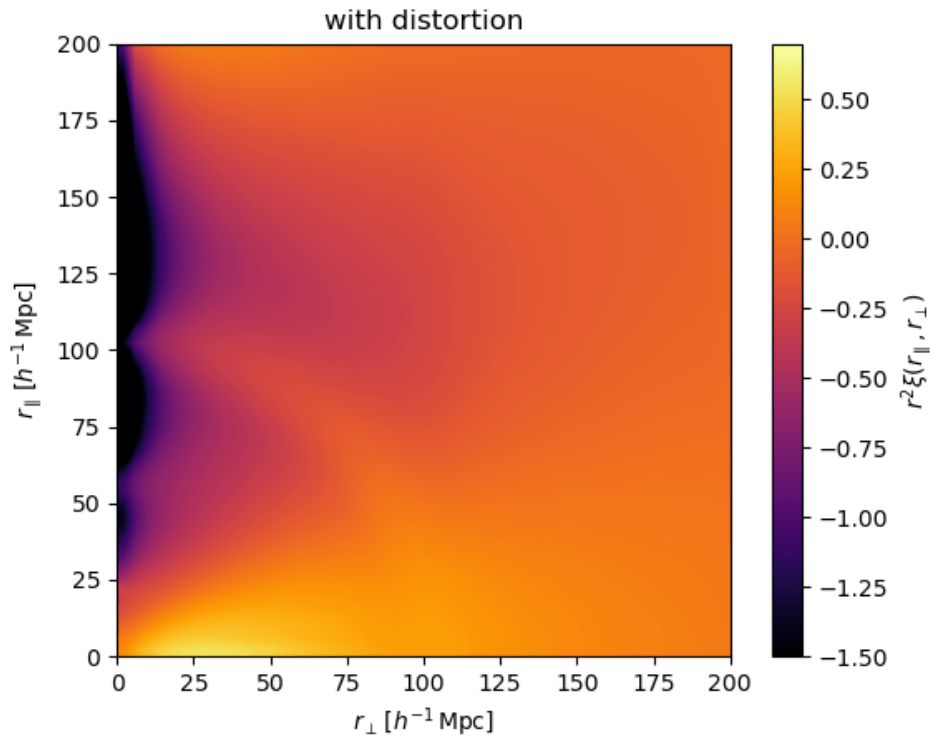
What's new in the Ly\(\alpha\) analysis?
Analysis pipeline mostly the same as DR1
Again, blind analysis to mitigate observer / confirmation biases (data vector-level blinding)
Improved modelling of metals and continuum-fitting distortions
New catalog of Damped Lyman-\(\alpha\) systems (masked)
Improved mocks and associated studies
Revised fitting range and priors on nuisance parameters
Include a small (0.3%) theory systematic uncertainty for non-linear BAO shift, \(\sigma_\mathrm{stat+syst} < 1.06 \sigma_\mathrm{stat}\)
What's new in the Ly\(\alpha\) analysis?
\(\Lambda\mathrm{CDM}\) constraints
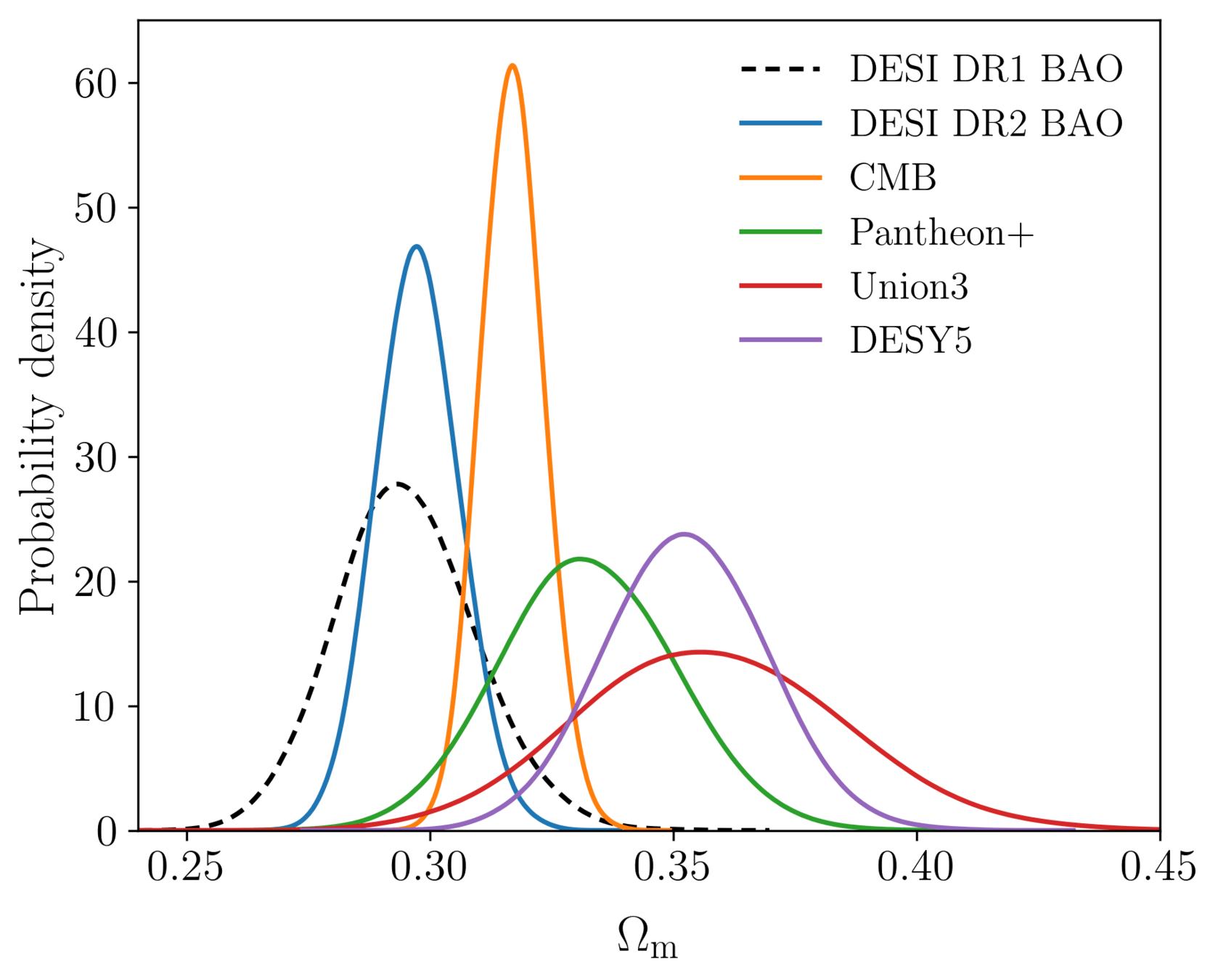
- DESI \(\Omega_\mathrm{m}\) lower than the CMB (\(1.8\sigma\))
-
DESI \(\Omega_\mathrm{m}\) lower than SN:
- Pantheon+: \(1.7\sigma\)
- Union3: \(2.1\sigma\)
- DESY5: \(2.9\sigma\)
Understanding tensions
DESI data release 1 (DR1)
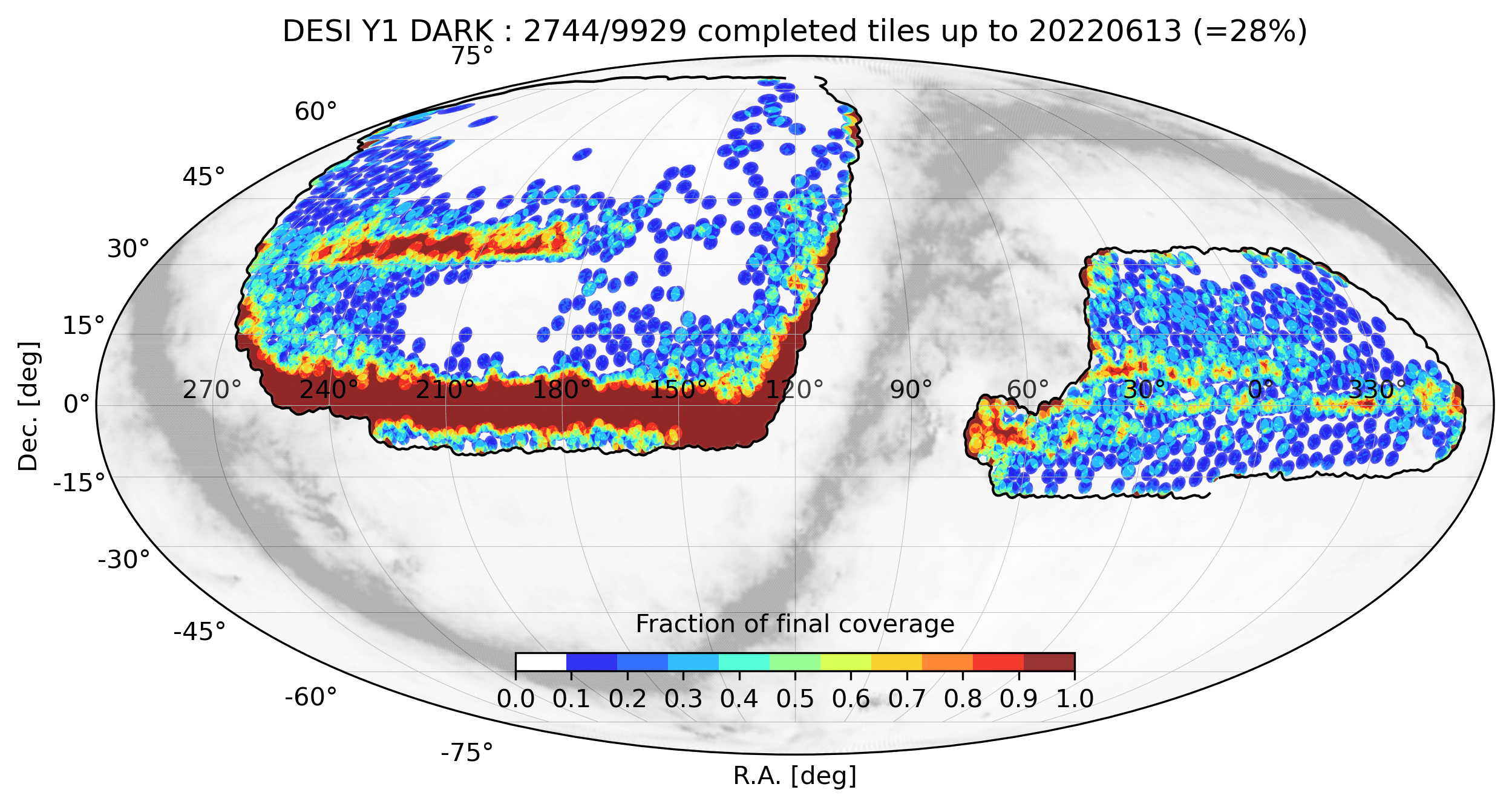
Observations from May 14th 2021 to June 12th 2022
DESI data release 2 (DR2)
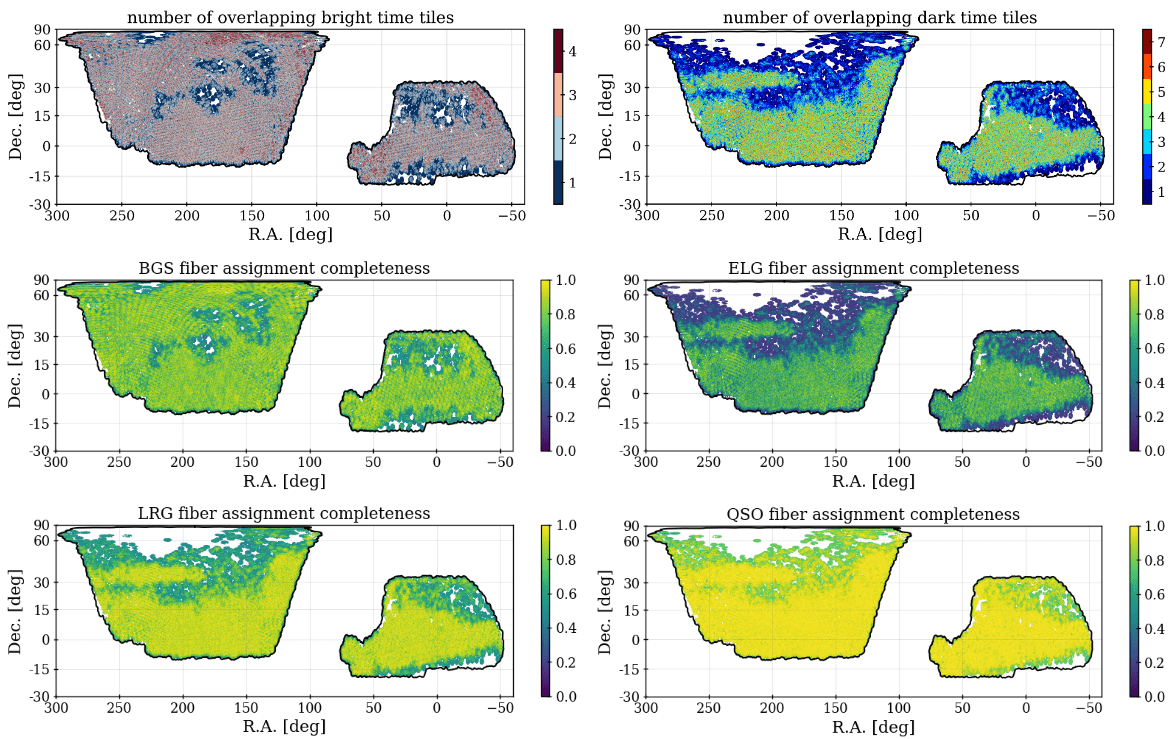
| asgn. comp. DR1 | # good z DR1 |
asgn. comp. DR2 | z. comp DR2 |
# of good z DR2 | |
| BGS | 64% | 0.3M | 76% | 99% | 1.2M |
| LRG | 69% | 2.1M | 83% | 99% | 4.5M |
| ELG | 35% | 2.4M | 54% | 74% | 6.5M |
| QSO | 87% | 1.2M | 94% | 68% | 2M |
more observations
Ly\(\alpha\) forest
Pre/post DESI
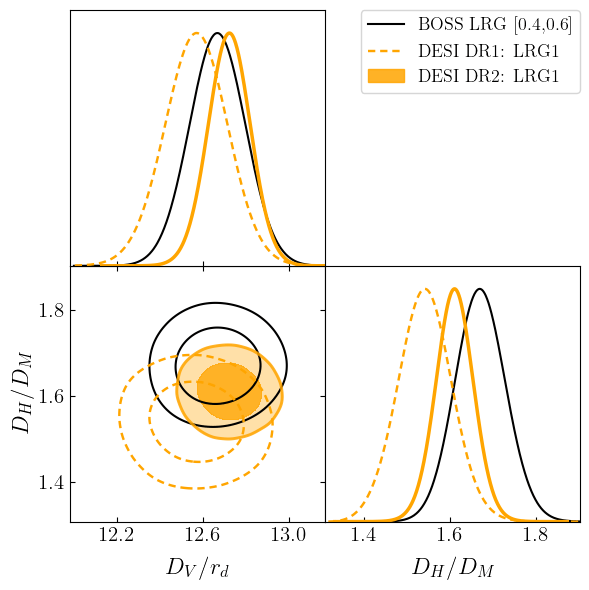
DESI vs BOSS/eBOSS
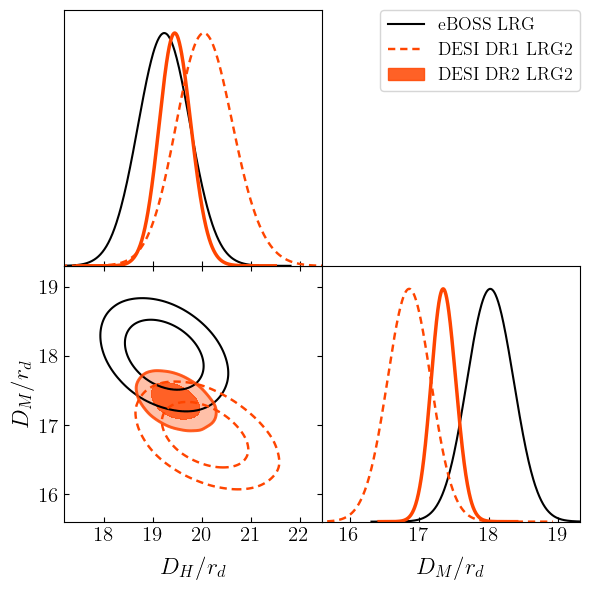
LRG2 (worst case)
\(2.8\sigma \, (\mathrm{DR1}) \Rightarrow 2.3\sigma \, (\mathrm{DR2})\)
Dark Energy Evolution
no phantom crossing
Null Energy Condition
DR2 footprint
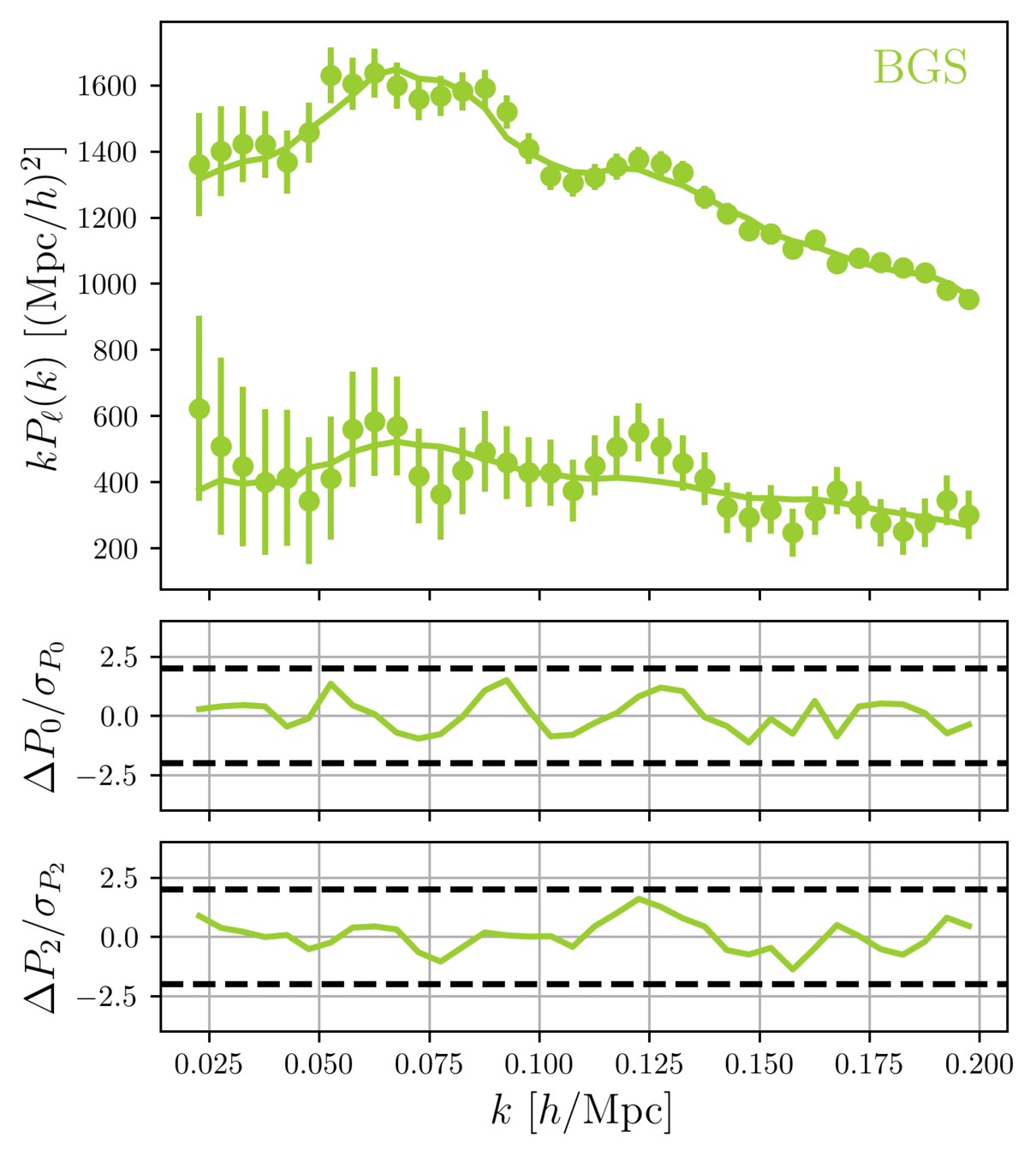
Full Shape measurements
clustering
We fit the "full shape" (FS) of the galaxy power spectrum multipoles
DR1 Full Shape + BAO
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
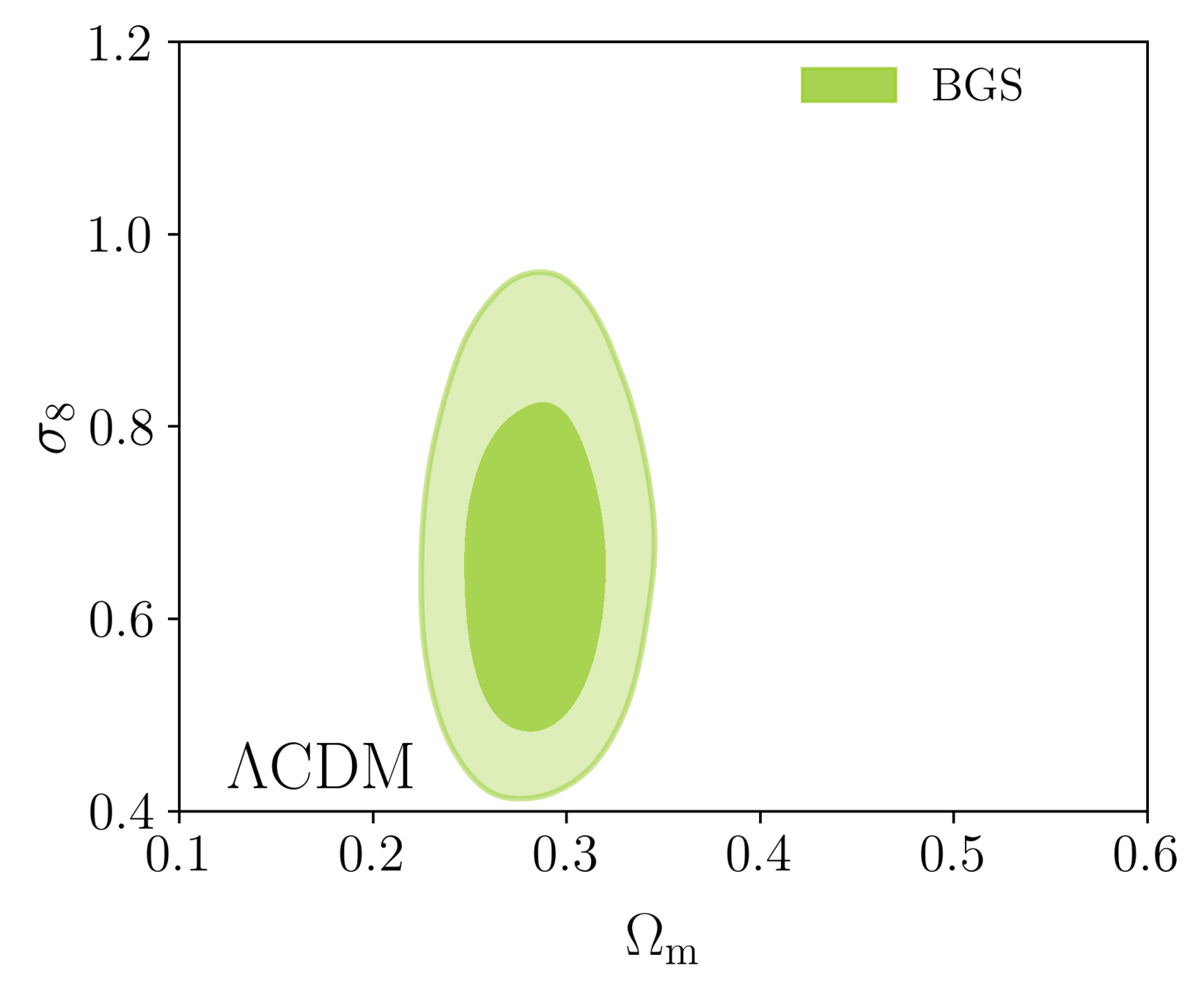
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
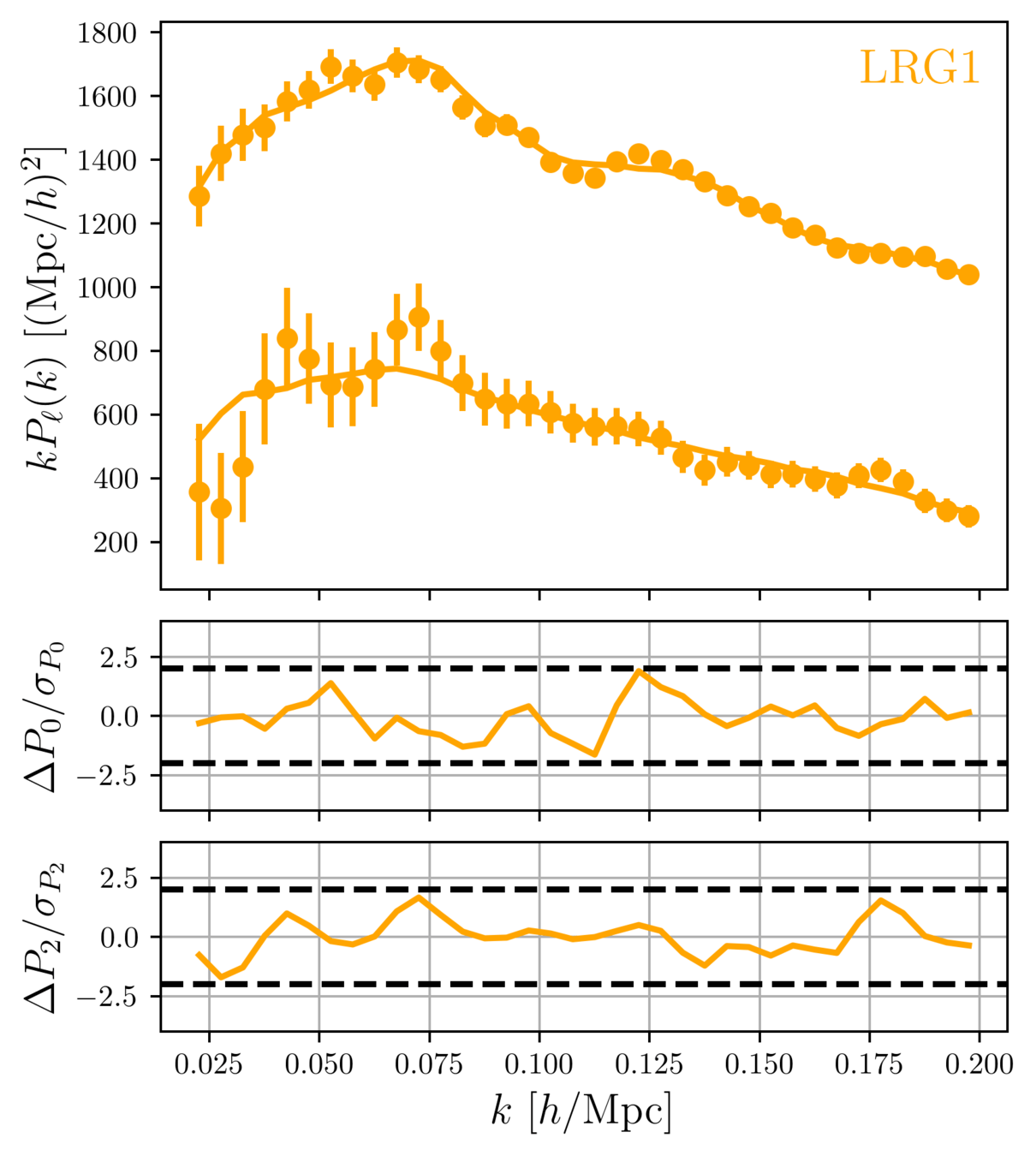
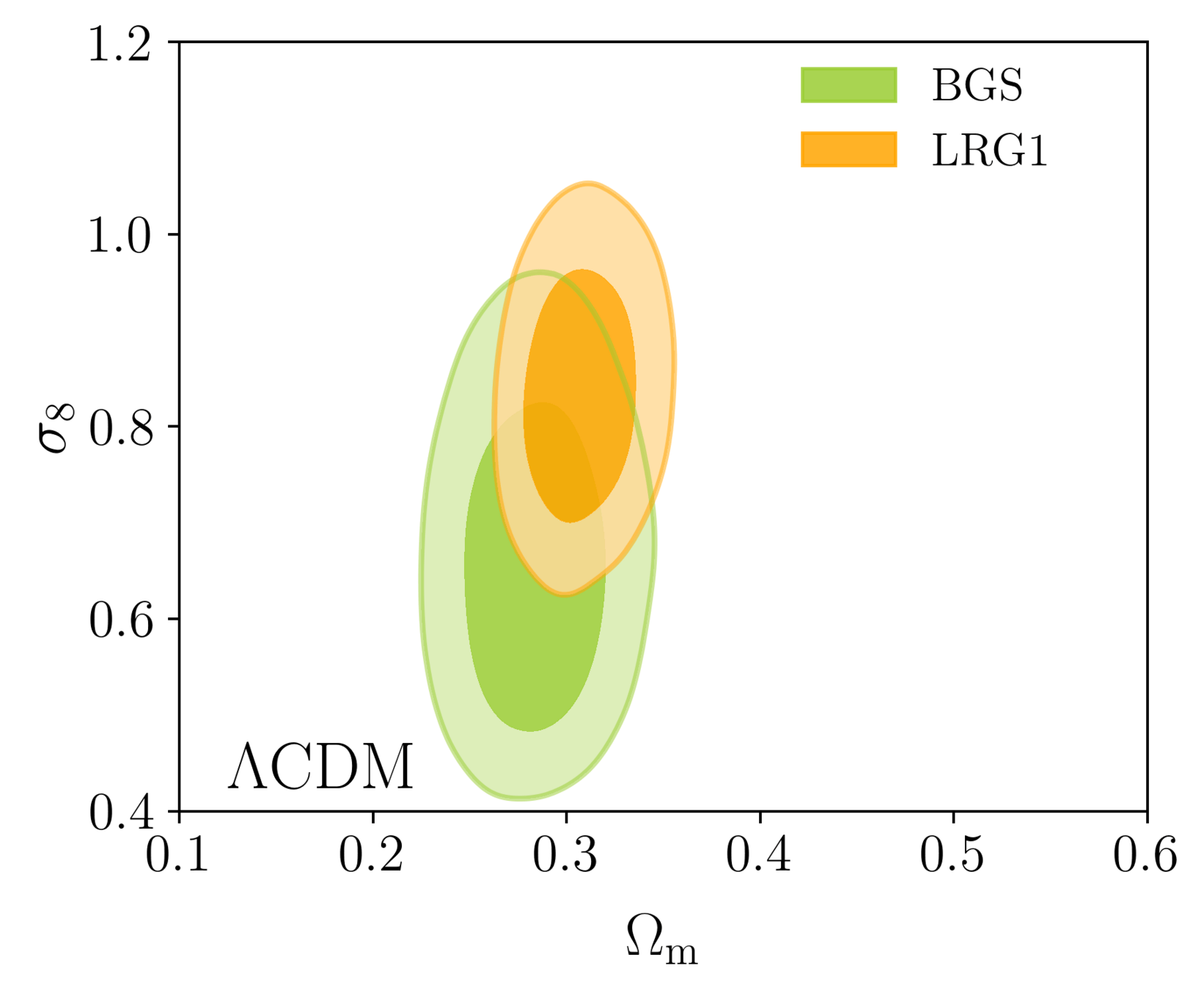
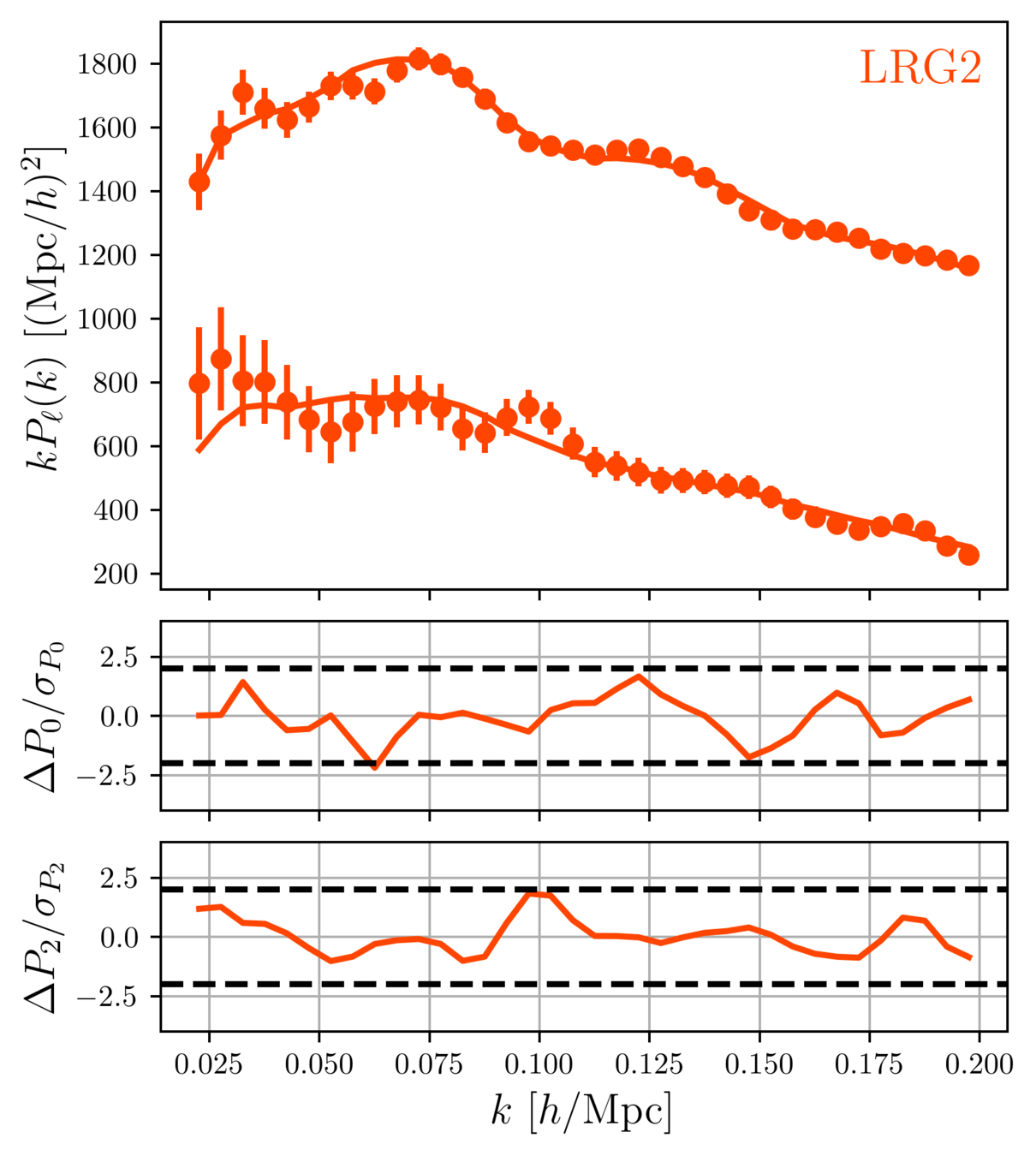
DR1 Full Shape + BAO
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
DR1 Full Shape + BAO
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
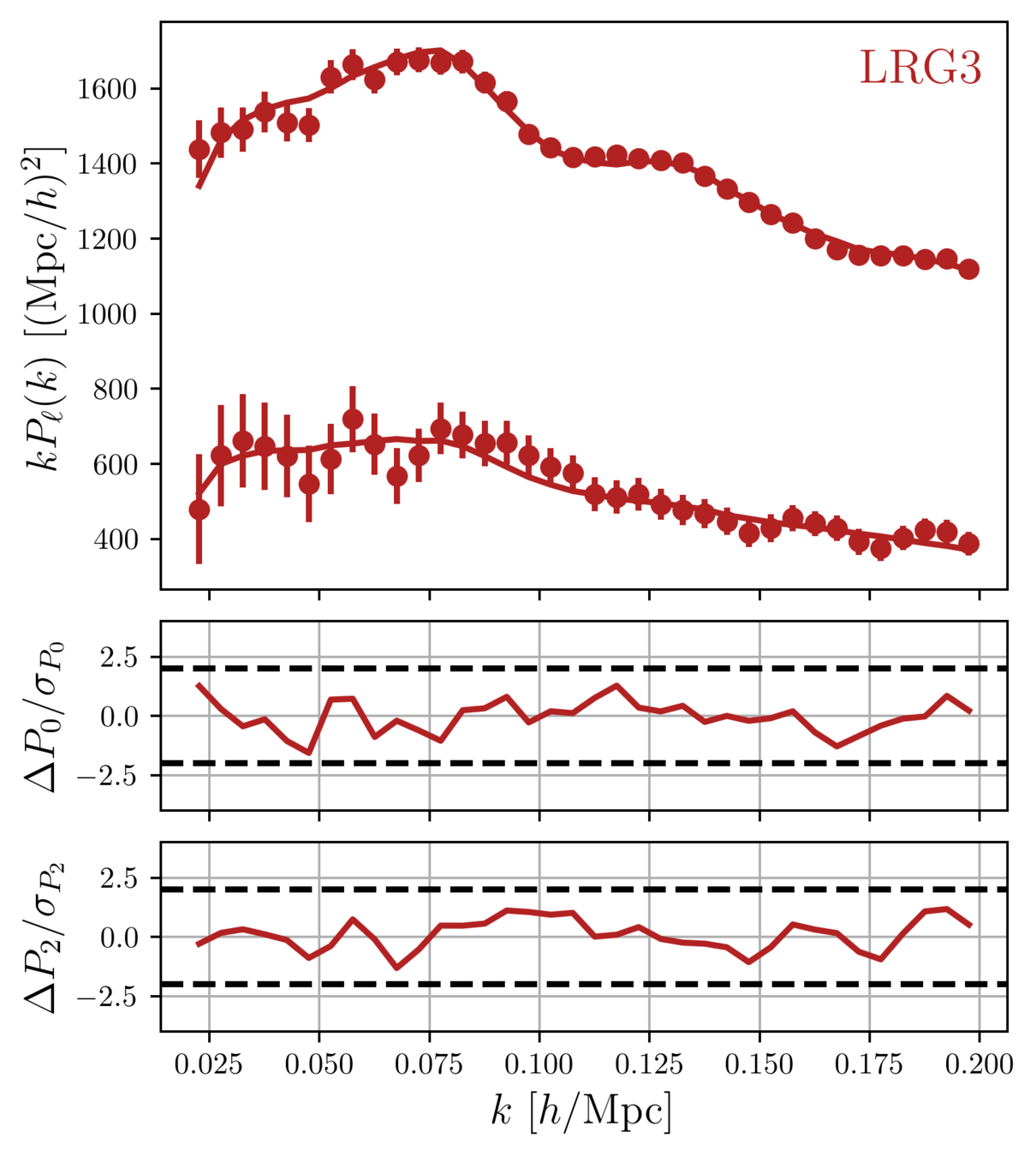
DR1 Full Shape + BAO
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
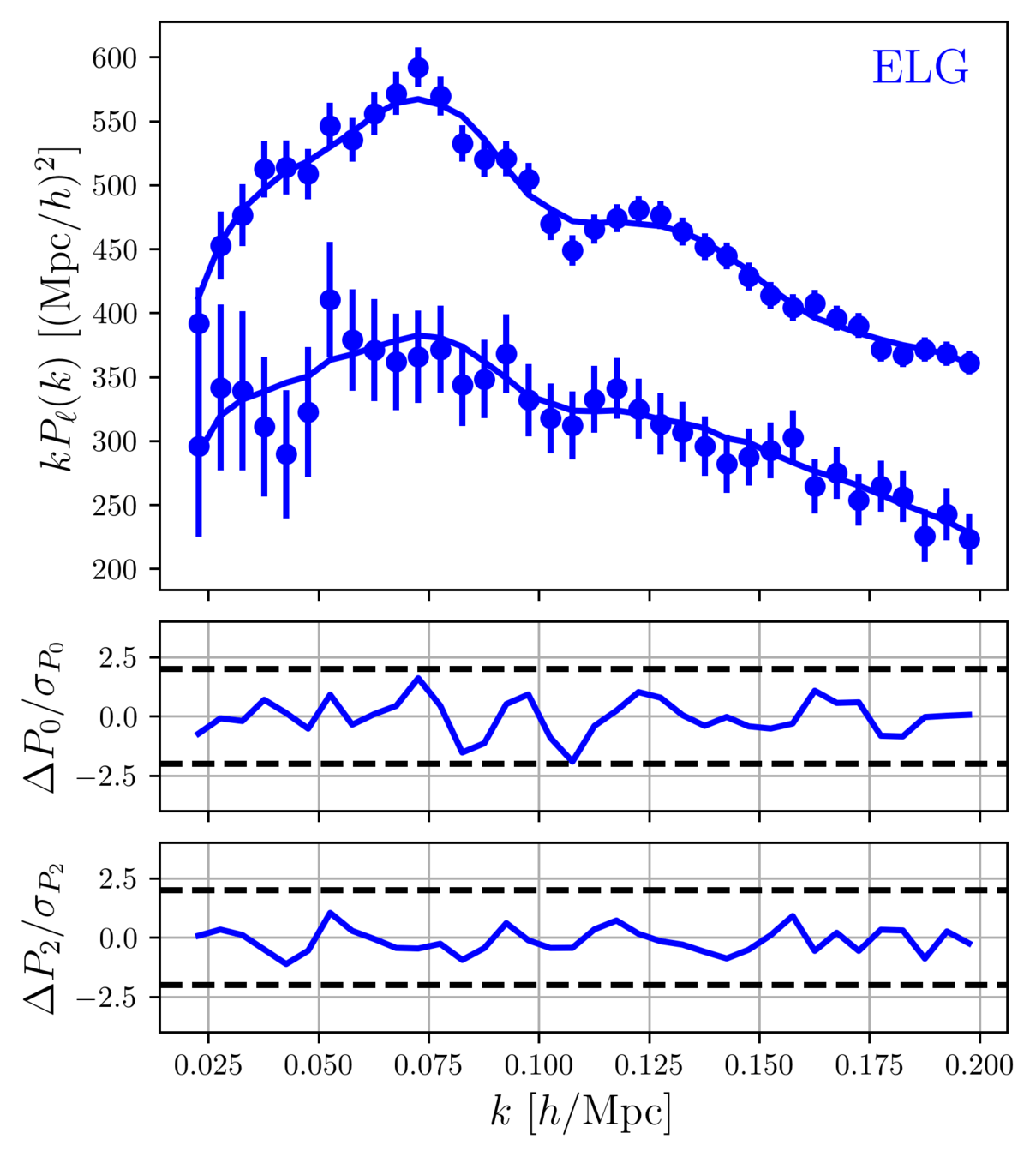
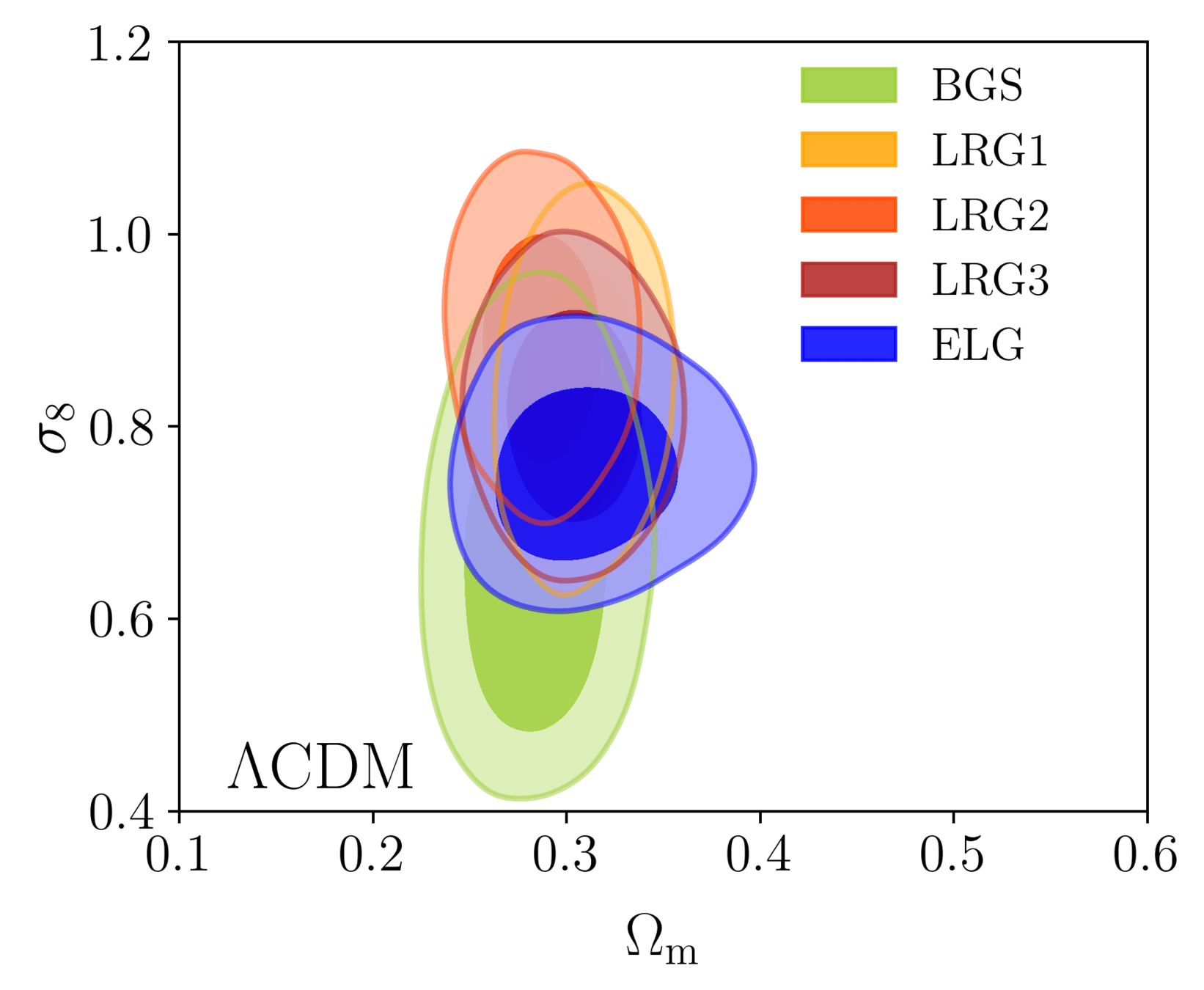
DR1 Full Shape + BAO
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
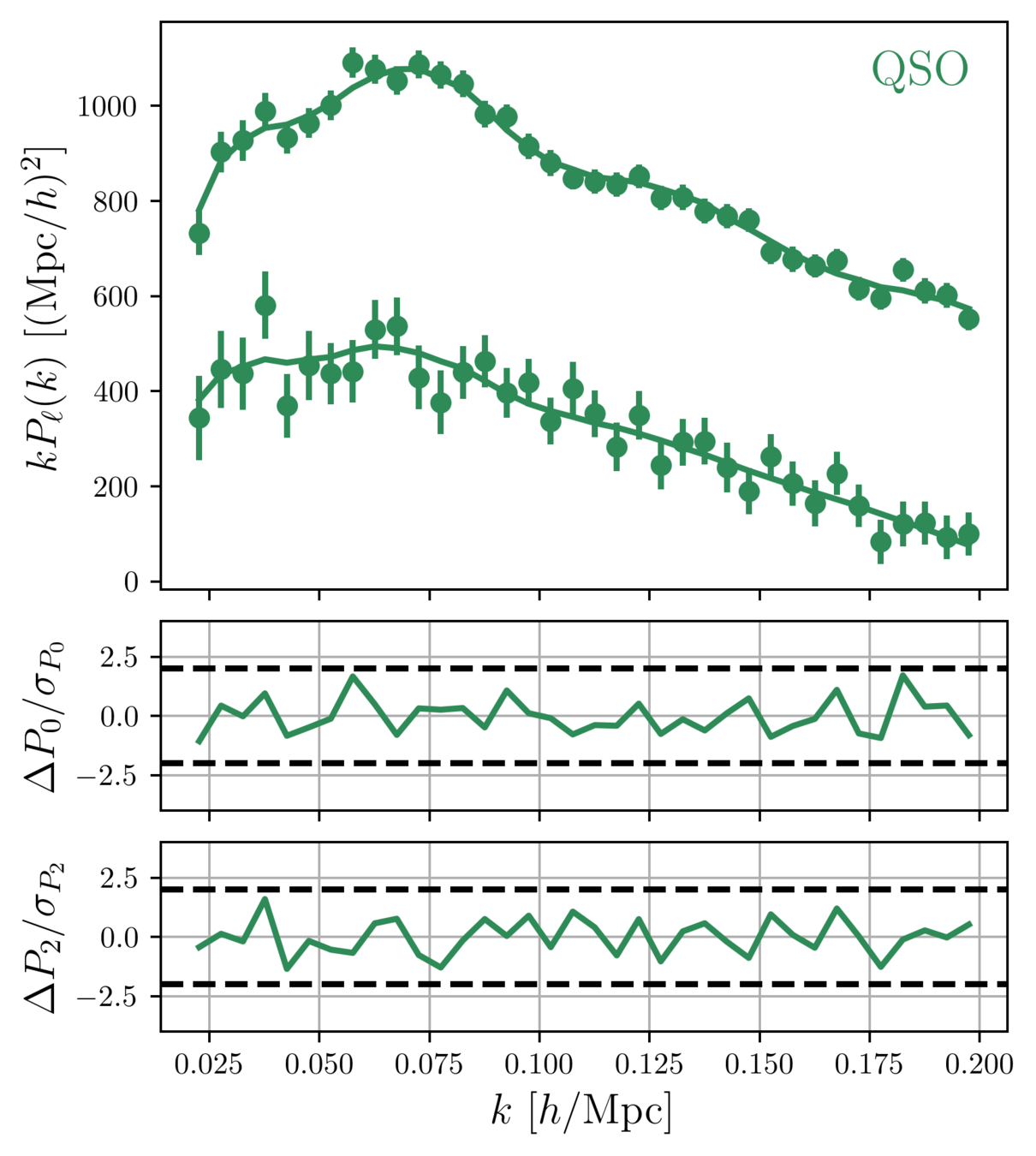
DR1 Full Shape + BAO
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.2962\pm 0.0095 & \mathbf{(3.2\%)} \\
\sigma_8 &= 0.842\pm 0.034 & \mathbf{(4.0\%)} \\
H_0 &= (68.56\pm 0.75) \, {\rm km\,s^{-1}\,Mpc^{-1}} & \mathbf{(1.1\%)}
\end{align*}}_{\textstyle \text{DESI + BBN + $n_{s10}$}}
\(\omega_\mathrm{b}\): BBN, \(n_\mathrm{s} \sim \mathcal{G}(0.9649, 0.042^2)\)
DR1 Full Shape + BAO
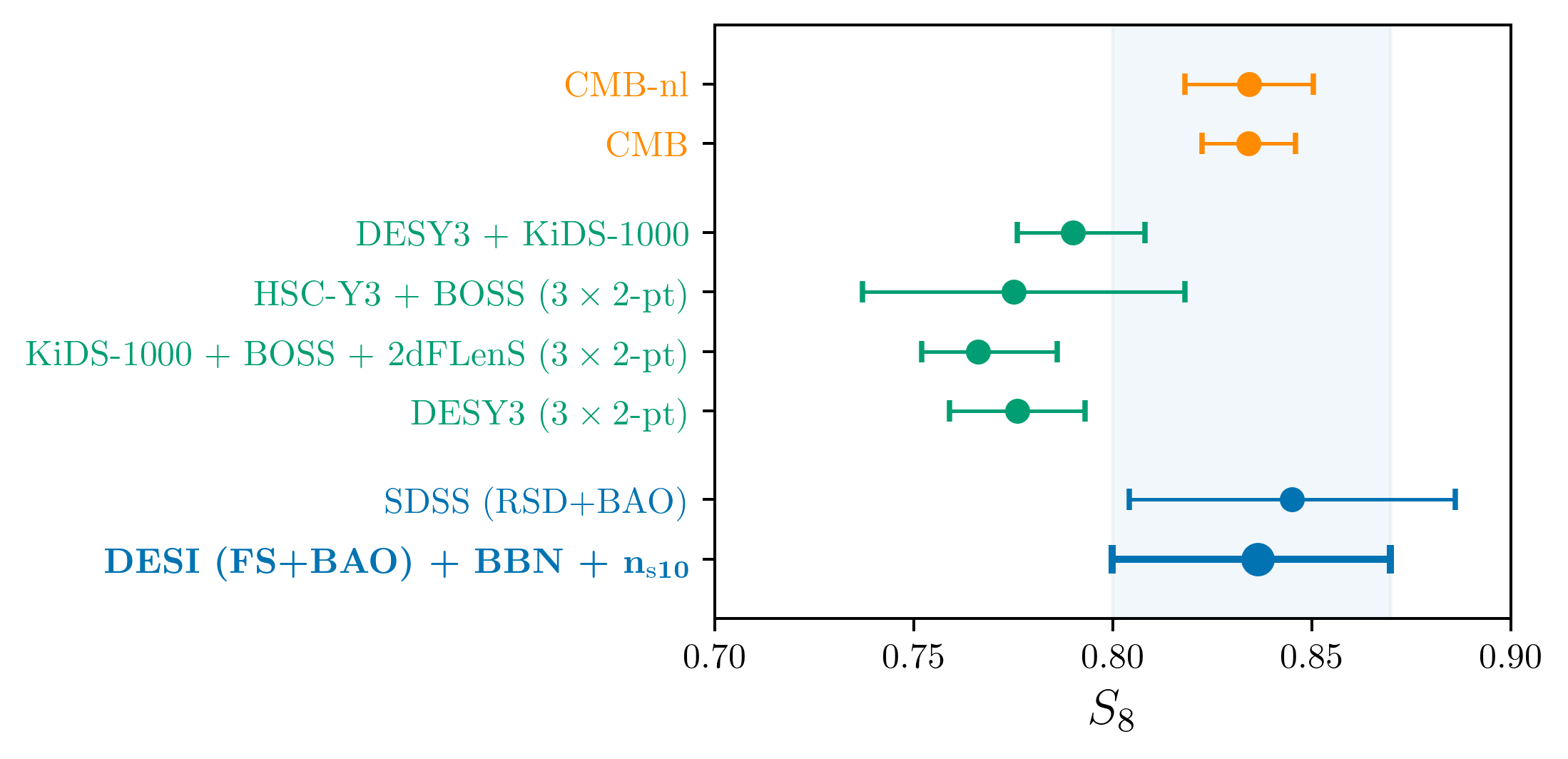
\(S_8\) constraints
- Consistency with SDSS
- In agreement with CMB
- Weak lensing prefers lower \(S_8\), but still consistent
\underbrace{
S_8 = 0.836 \pm 0.035
}_{\textstyle \text{\color{blue}{DESI + BBN + $n_{s10}$}}}
\(S_8 = \sigma_8 (\Omega_\mathrm{m} / 0.3)^{0.5}\) best constrained by weak lensing surveys
Modified gravity constraints
Perturbed FLRW metric
\(ds^2=a(\tau)^2[-(1+2\orange{\Psi})d\tau^2+(1-2\orange{\Phi})\delta_{ij}dx^i dx^j]\)
At late times:
(mass) \(k^2\orange{\Psi} = -4\pi G a^2 \green{\mu(a,k)} \blue{\sum_i\rho_i\Delta_i}\)
(light) \(k^2(\orange{\Phi} + \orange{\Psi})=-8\pi G a^2 \green{\Sigma(a,k)} \blue{\sum_i\rho_i\Delta_i}\)
gravitational potentials
density perturbations
\mu(a) = 1 + \frac{\Omega_\Lambda(a)}{\Omega_\Lambda} \green{\mu_0}
\Sigma(a) = 1 + \frac{\Omega_\Lambda(a)}{\Omega_\Lambda} \green{\Sigma_0}
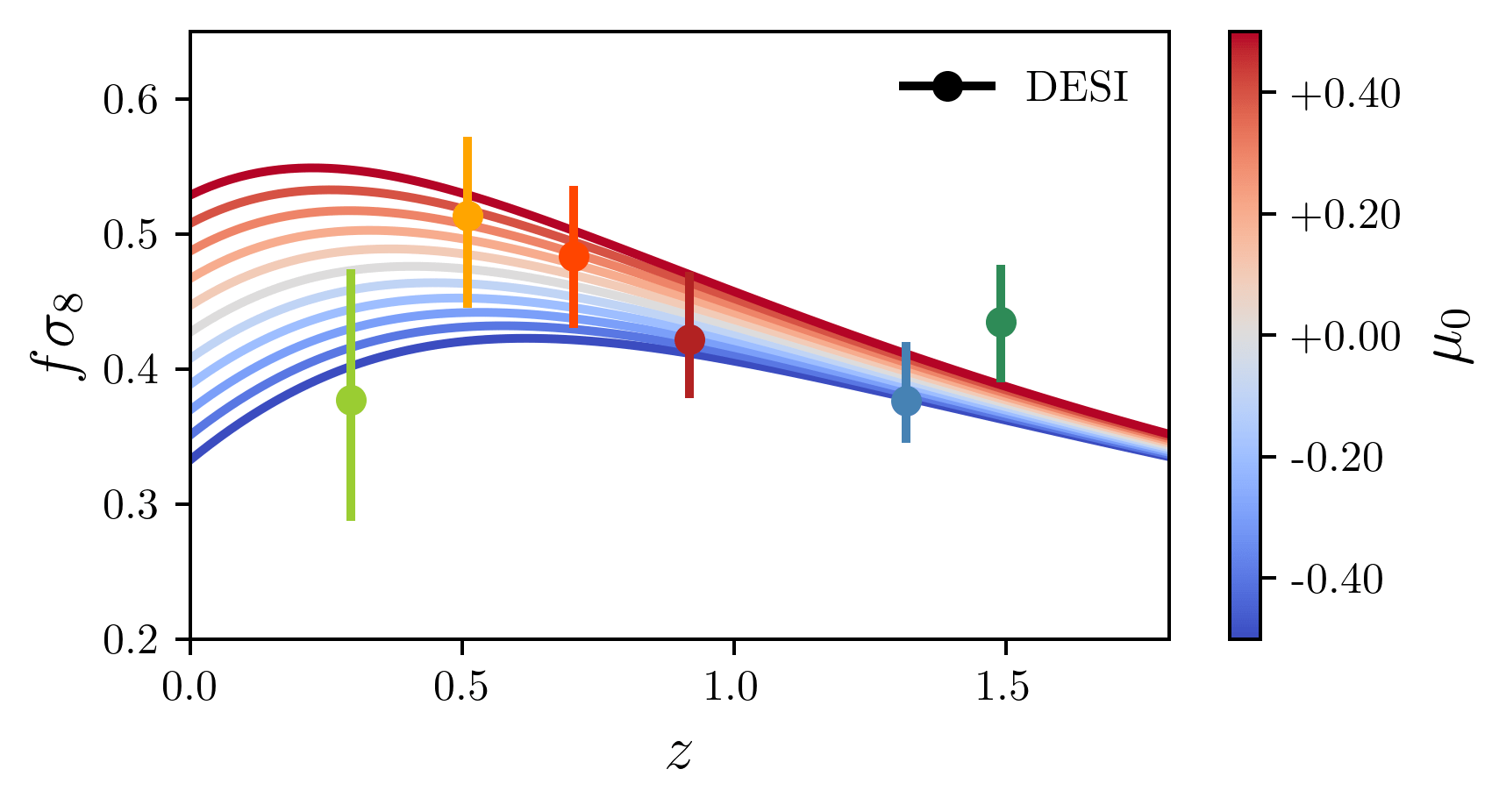
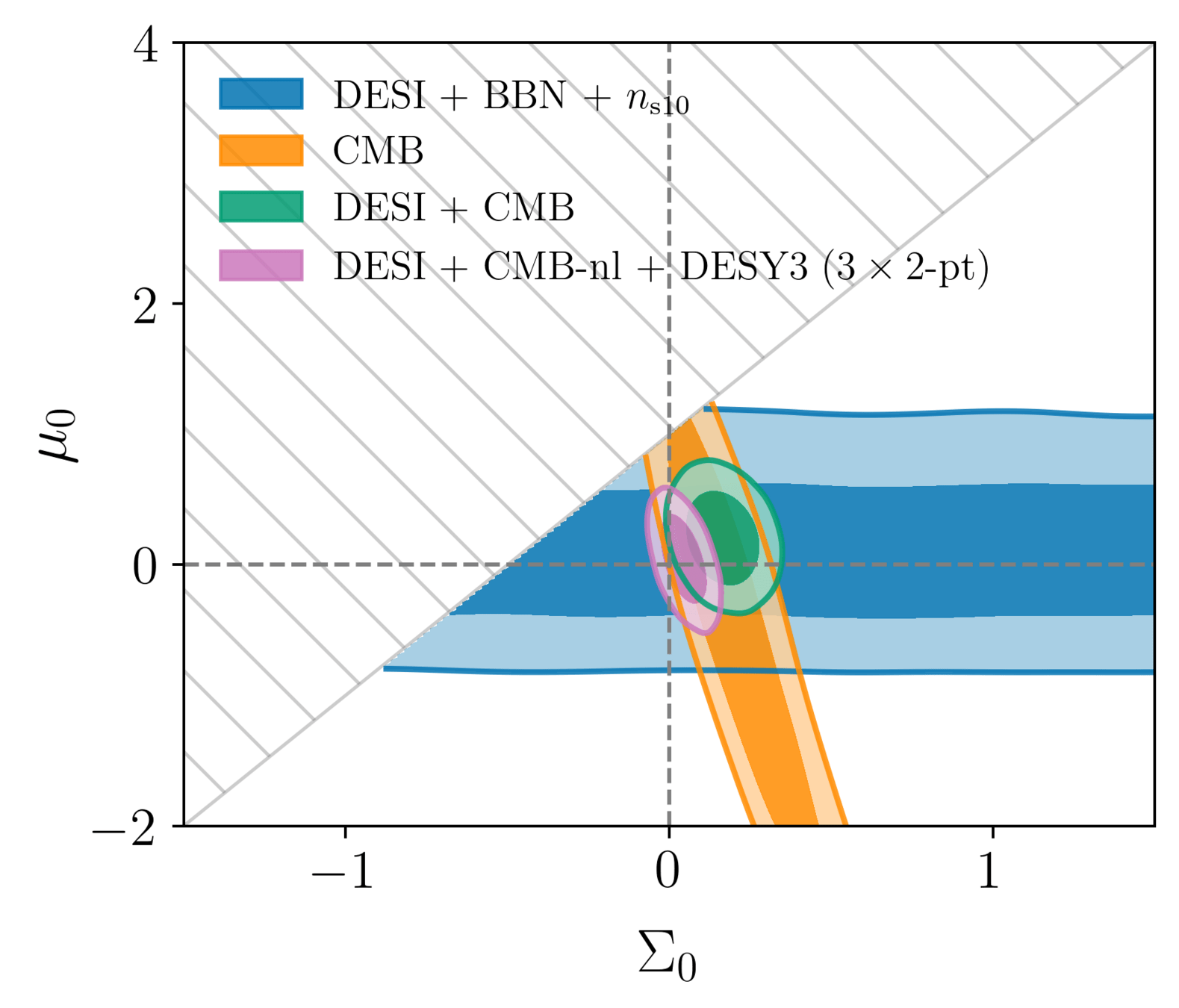
Modified gravity constraints
\(\Sigma_0\) constrained by
- CMB (ISW and lensing)
- galaxy lensing
\underbrace{\begin{align*}
\mu_0 &= 0.04\pm 0.22 \\
\Sigma_0 &= 0.045\pm 0.046
\end{align*}}_{\textstyle \text{\color{purple}{DESI + CMB-nl + DESY3 ($3\times 2$-pt)}}}
\underbrace{
\mu_0 = 0.11^{+0.45}_{-0.54}
}_{\textstyle \text{\color{blue}{DESI + BBN + $n_{\mathrm{s}10}$}}}
compared to CMB-nl + DESY3 (3x2pt) only: \(\sigma(\mu_0) / 2.5\), \(\sigma(\Sigma_0) / 2\)
DESI constrains
Window matrix: another look
Let's just Taylor expand the observed power spectrum \(P_o\) as a function of the theory \(\theta_t\) (e.g. \(P_t\)) around fiducial values:
P_o = P_o(\theta_t^\mathrm{fid}) + \left.\frac{d P_o}{d \theta_t}\right\rvert_\mathrm{fid} (\theta_t - \theta_t^\mathrm{fid})
could come from the average of many mocks
then the window matrix \(\left.\frac{d P_o}{d \theta_t}\right\rvert_\mathrm{fid}\) just multiplies the deviation w.r.t. the fiducial
\(\Rightarrow\) in the limit that \(\theta_t^\mathrm{fid}\) is close to the truth, just require \(\left.\frac{d P_o}{d \theta_t}\right\rvert_\mathrm{fid}\) to be as accurate as the covariance matrix! (i.e. ~ only impacts the final \(\theta_t\) uncertainties)
Baryon acoustic oscillations (BAO)
Credits: Julian Bautista
Waterloo_November2025
By Arnaud De Mattia
