DESI 2024: Survey Overview and Cosmological constraints from Baryon Acoustic Oscillations
Arnaud de Mattia
CEA Saclay
IRN, June 11th
Thanks to our sponsors and
72 Participating Institutions!
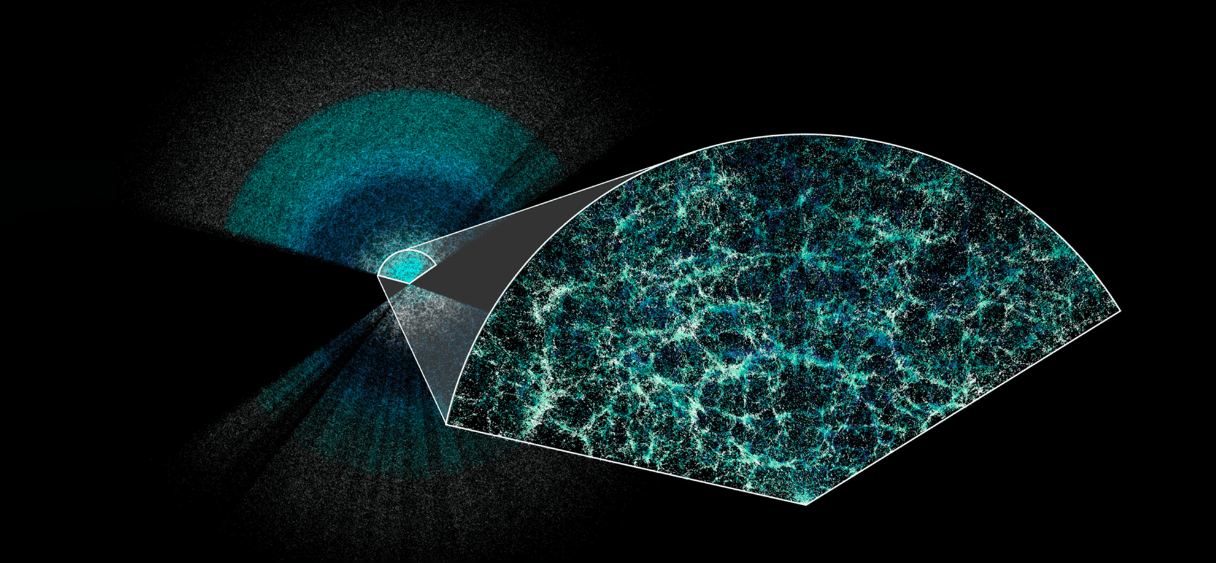
DESI 3D Map
Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z
DESI 3D Map
Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z
DESI Y5 galaxy samples
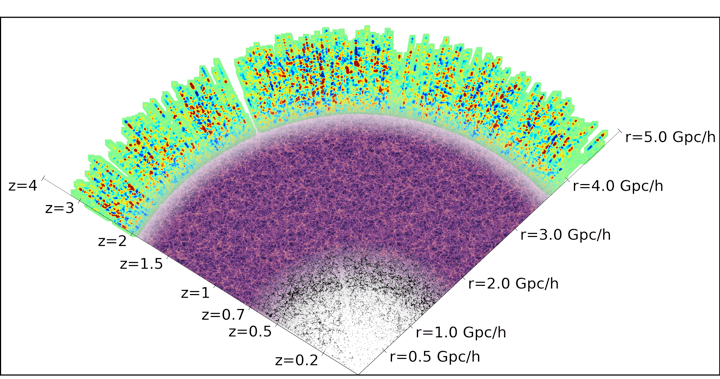
13.5 million Bright Galaxies
0 < z < 0.4
8 million LRGs
0.4 < z < 0.8
16 million ELGs
0.6 < z < 1.6
3 million QSOs
Lya \(1.8 < z\)
Tracers \(0.8 < z < 2.1\)
Y5 \(\sim 40\) M galaxy redshifts!
From images to redshifts
imaging surveys (2014 - 2019) + WISE (IR)
target selection
spectroscopic observations
spectra and redshift measurements
Mayall Telescope
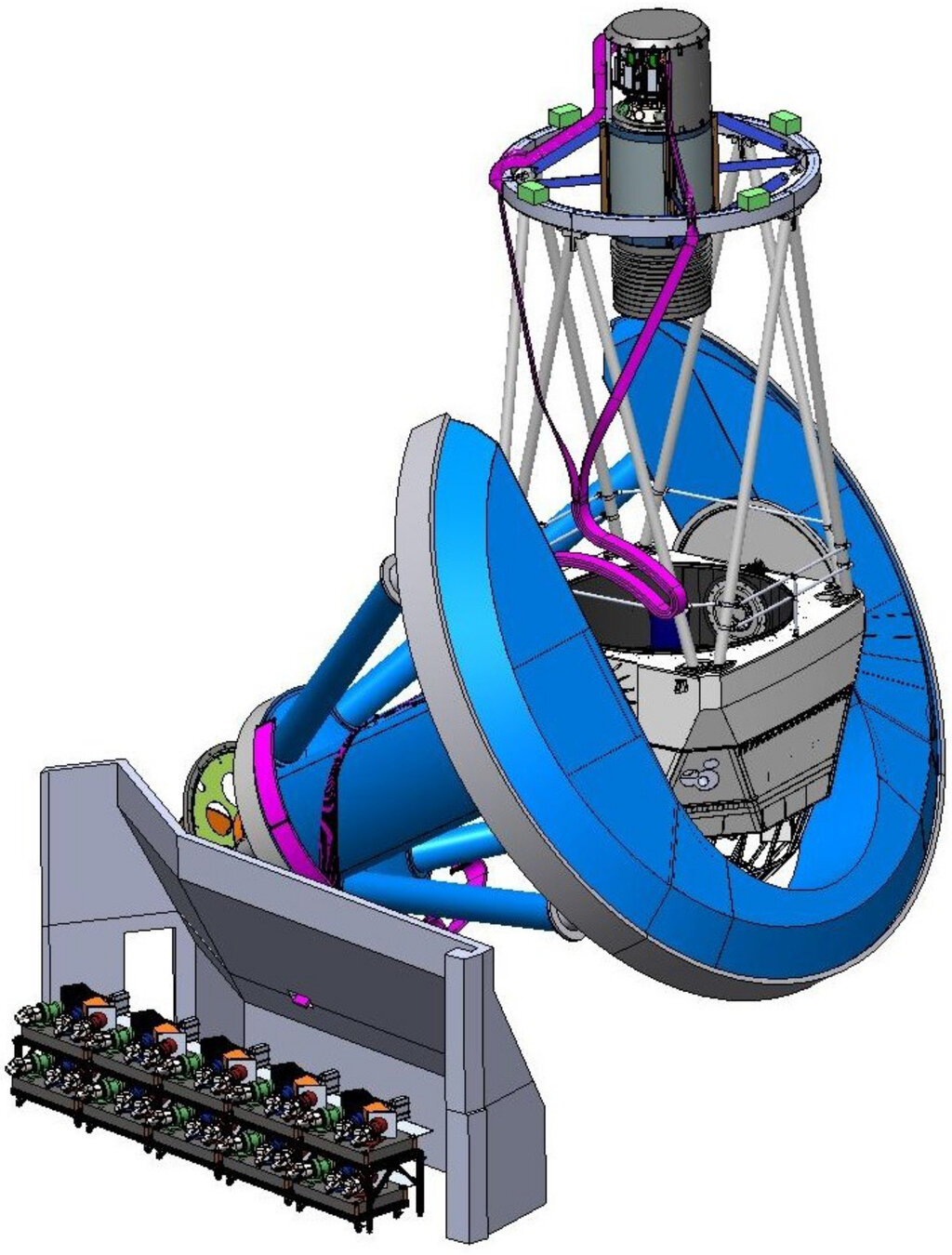
focal plane 5000 fibers
fiber view camera
wide-field corrector FoV \(\sim 8~\mathrm{deg}^{2}\)
ten 3-channel spectrographs
49 m, 10-cable fiber run
Kitt Peak, AZ
Focal plane: 5000 robotic positioners
86 cm
0.1 mm
Exposure time (dark): 1000 s
Configuration of the focal plane
CCD readout
Go to next pointing
140 s
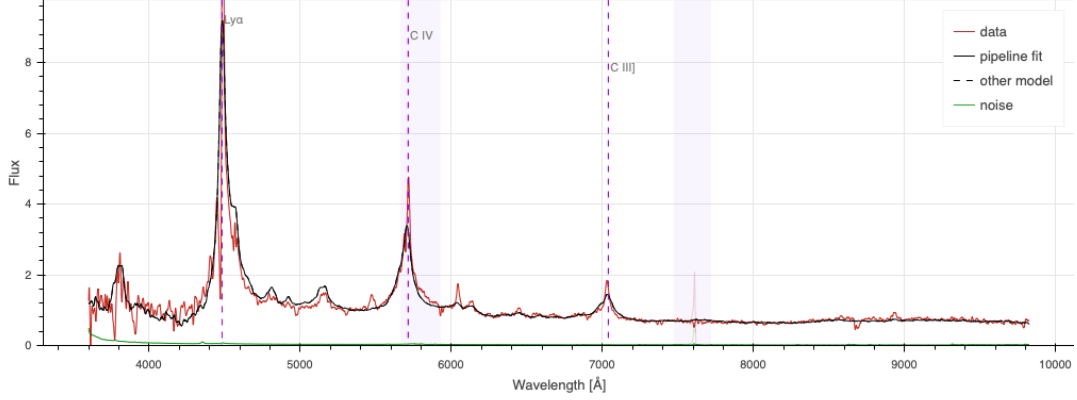
Spectroscopic pipeline
wavelength
fiber number
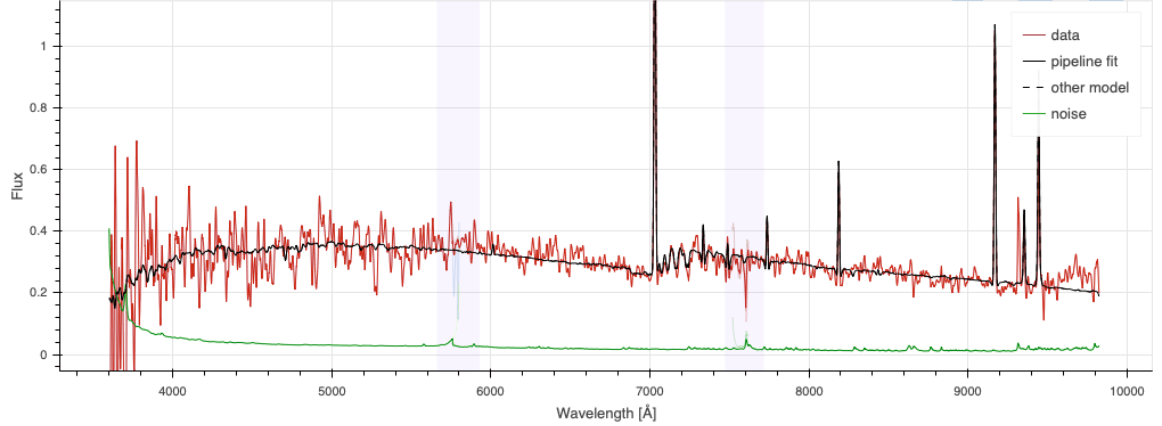
\(z = 2.1\) QSO
\(z = 0.9\) ELG
Ly\(\alpha\)
CIV
CIII
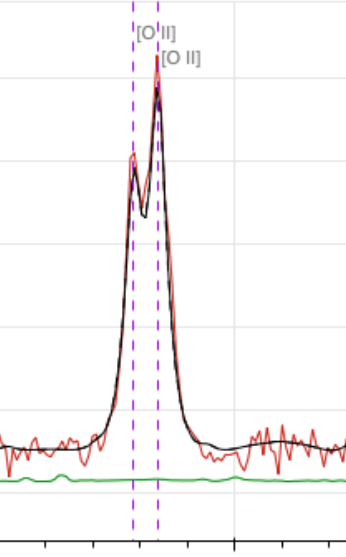
[OII] doublet at \(2727 \AA\) up to \(z = 1.6\)
[OII]
Ly\(\alpha\) at \(1216 \AA\) down to \(z = 2.0\)
DESI Y5 forecasts
Survey Validation (arXiv:2306.06307)
BAO and RSD constraints at the end of the survey (\( \Delta z = 0.1 \))
Ly\(\alpha\)
DESI Y5 forecasts
Survey Validation (arXiv:2306.06307)
BAO and RSD constraints at the end of the survey (\( \Delta z = 0.1 \))
Ly\(\alpha\)
(w/ Planck)
DESI data release 1 (DR1)
Observations from May 14th 2021 to June 12th 2022
Final survey
- dark time (LRG, ELG, QSO): 7 visits
- bright time (BGS): 5 visits
- 14,000 \(\mathrm{deg}^2\)
DESI data release 1 (DR1)
5.7 million unique redshifts at z < 2.1 and > 420,000 Ly\(\alpha\) QSO at z > 2.1
Release of DESI DR1 (BAO) results
April 4th 2024
First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/
• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements
Release of DESI DR1 (BAO) results
April 4th 2024
First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/
• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements
Baryon acoustic oscillations
Sound waves in primordial plasma
At recombination (\(z \sim 1100\))
- plasma changes to optically thin
- baryons decouple from photons
- sound wave stalls
Baryon acoustic oscillations
Sound waves in primordial plasma
At recombination (\(z \sim 1100\))
- plasma changes to optically thin
- baryons decouple from photons
- sound wave stalls
spherical shell in the distribution of galaxies, of radius the distance that sound waves travelled
= sound horizon scale at the drag epoch \( r_\mathrm{d} \sim 150 \; \mathrm{Mpc} \sim 100 \; \mathrm{Mpc}/h \)
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
z
\theta_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{M}(z)
BAO measurements
transverse comoving distance
sound horizon \(r_d\)
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
- along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
BAO measurements
z
\Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z)
Hubble distance
sound horizon \(r_d\)
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
- along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
At multiple redshifts \(z\)
BAO measurements
z_1
z_2
z_3
Correlation functions
Excess probability to find 2 galaxies separated by a separation s
Correlation functions
BAO peak
Power spectra
Power spectra
BAO wiggles
Some fits: configuration space
isotropic measurement
anisotropic measurement
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)
Some fits: Fourier space
isotropic measurement
anisotropic measurement
\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)
Non-linear evolution
Non-linear structure growth and peculiar velocities blur and shrink (slightly) the ruler
Eisenstein et al. 2008, Padmanabhan et al. 2012
Density field reconstruction
Estimates Zeldovich displacements from observed field and moves galaxies back: refurbishes the ruler (improves precision and accuracy)
reconstruction
Density field reconstruction
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
5.7 million unique redshifts
Effective volume \(V_\mathrm{eff} = 18 \; \mathrm{Gpc}^{3}\)
\(3 \times \) bigger than SDSS!
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
- Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
(\mathrm{R.A.}, \mathrm{Dec.}, z) \Longrightarrow (x, y, z) \Longrightarrow (\mathrm{R.A.}^\prime, \mathrm{Dec.}^\prime, z^\prime)
fiducial cosmology
blinded cosmology (\(\Omega_\mathrm{m}, w_0, w_a\))
(random & unknown)
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
- Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
(\mathrm{R.A.}, \mathrm{Dec.}, z) \Longrightarrow (x, y, z) \Longrightarrow (\mathrm{R.A.}^\prime, \mathrm{Dec.}^\prime, z^\prime)
fiducial cosmology
blinded cosmology (\(\Omega_\mathrm{m}, w_0, w_a\))
(random & unknown)
+ RSD blinding: change reconstructed peculiar velocities
+ \(f_\mathrm{NL}\) blinding: add clustering-dependent signal on large scales with weights
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
- Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
- Theory developments in BAO fitting code
P_\mathrm{gg}(k, \mu) = \mathcal{B}(k, \mu) P_\mathrm{nw}(k) + \mathcal{C}(k, \mu) P_\mathrm{w}(k) + \orange{\mathcal{D}(k, \mu)}
Chen, Howlett et al. 2024
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
- Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
- Theory developments in BAO fitting code
- New and improved reconstruction methods
- New combined tracer method used for overlapping galaxy samples (LRG and ELG in \(0.8 < z < 1.1\))
DESI DR1 BAO analysis
- Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
- Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
- Theory developments in BAO fitting code
- New and improved reconstruction methods
- New combined tracer method used for overlapping galaxy samples (LRG and ELG in \(0.8 < z < 1.1\))
- Unified BAO pipeline applied to all (discrete) tracer / redshift bins consistently
Tests of systematic errors
Considered many possible sources of systematic errors using simulations and data:
- observational effects (imaging systematics, fiber collisions)
- BAO reconstruction (2 algorithms compared)
- covariance matrix construction
- incomplete theory modelling
- choice of fiducial cosmology
- galaxy-halo (HOD) model uncertainties
no systematics detected
systematics << statistics
Max effect: \(\sigma_\mathrm{stat. + syst.} < 1.05 \sigma_\mathrm{stat.}\)
Release of DESI DR1 (BAO) results
April 4th 2024
First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/
• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements
Ly\(\alpha\) forest
Absorption in QSO spectra by neutral hydrogen in the intergalactic medium: \(\lambda_\mathrm{abs} = (1 + z_\mathrm{HI}) \times 1215.17 \; \AA \)
Transmitted flux fraction \(F = e^{-\tau}\) probes the fluctuation in neutral hydrogen density, \(\tau \propto n_\mathrm{HI} \)
credit: Andrew Pontzen
Ly\(\alpha\) correlation functions in DESI DR1
Ly\(\alpha\) - Ly\(\alpha\)
Ly\(\alpha\) - QSO
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
>420,000 Ly\(\alpha\) QSO at z > 2.1
\(2 \times \) more than SDSS!
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function:
- cosmo signal
P_{\mathrm{Ly}\alpha}(k, \mu) = \blue{b^{2} (1 + \beta \mu^2)^2} \orange{P_\mathrm{lin}(k, \mu)} \green{F_\mathrm{NL}(k, \mu)}
linear bias + RSD
hydro-sim
BAO
\mu = r_\parallel / \sqrt{r_\parallel^2 + r_\perp^2}
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function:
- cosmo signal
- high-column density
- metal absorbers
r_\parallel \propto \left\vert\frac{1}{\lambda_{\mathrm{Ly}\alpha}} - \frac{1}{\lambda_{\mathrm{metal}}}\right\vert
SiII
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function:
- cosmo signal
- high-column density
- metal absorbers
- correlated noise (sky subtraction)
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function
physical model fit
+ broadband polynomial
broadband: \(< 0.1\sigma\)
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function
- Cross-covariance matrix
Correlation matrix
smoothed jackknife, validated with mocks
10% impact on BAO uncertainty
DESI DR1 Ly\(\alpha\) BAO analysis
- Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
- First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
- Modelling of the correlation function
- Cross-covariance matrix
- Very stable results, systematic uncertainty neglected
Tests of systematic errors
tests with same dataset (not red): shifts \(< \sigma_\mathrm{stat}/3\)
tests with varying datasets (red): shifts consistent with stat.
Release of DESI DR1 (BAO) results
April 4th 2024
First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/
• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
- along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
- low S/N, isotropic average: \( D_\mathrm{V}(z) / r_\mathrm{d} = (z D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}\)
BAO measurements
BAO measures ratios of distances over the sound horizon scale at the drag epoch ["standard ruler"] \(r_\mathrm{d}\)
Let's factor out the \(h\) terms:
- \(\color{blue}{[D_\mathrm{M}(z) h] (\Omega_\mathrm{m}, f_\mathrm{DE}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)
- \( \color{blue}{[D_\mathrm{H}(z) h] (\Omega_\mathrm{m}, f_\mathrm{DE}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)
BAO measurements at different \(z\) constrain:
- energy content \( \color{blue}{(\Omega_\mathrm{m}, f_\mathrm{DE}, ...)} \)
- constant-over-\(z\) product \(\color{orange}{r_\mathrm{d} h}\) i.e. \(\color{orange}{H_{0} r_\mathrm{d}}\)
These quantities directly relate to base cosmological parameters
BAO measurements
\(h = H_{0} / [100\; \mathrm{km}/\mathrm{s} / \mathrm{Mpc}]\)
\(\Omega_\mathrm{m}\) fractional energy density of matter
\(f_\mathrm{DE}\) dark energy
\(\Omega_\mathrm{K}\) curvature
\(\Omega_{b}\) baryons
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
Consistent with each other,
and complementary
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.295 \pm 0.015 & \mathbf{(5.1\%)} \\
H_{0} r_\mathrm{d} &= (101.8 \pm 1.3) \, [100 \, \mathrm{km} \, \mathrm{s}^{-1}] & \mathbf{(1.3\%)}
\end{align*}}_{\textstyle \text{\color{black}{DESI}}}
Consistency with other probes
DESI Y1 BAO consistent with:
Consistency with other probes
DESI Y1 BAO consistent with:
Consistency with other probes
DESI Y1 BAO consistent with:
- SDSS eBOSS Collaboration, 2020
- primary CMB: Planck Collaboration, 2018 and CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
Consistency with other probes
DESI Y1 BAO consistent with:
- SDSS eBOSS Collaboration, 2020
- primary CMB: Planck Collaboration, 2018 and CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
\underbrace{
\Omega_\mathrm{m} = 0.3069 \pm 0.0050 \; \mathbf{(1.6\%)}
}_{\textstyle \text{\green{DESI + CMB}}}
- BAO constrains \( r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h \)
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \Omega_\mathrm{b} h^{2}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
- \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by light element abundance from Big Bang Nucleosynthesis (BBN): Schöneberg et al., 2024
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
- \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by light element abundance from Big Bang Nucleosynthesis (BBN): Schöneberg et al., 2024
\(\implies\) constraints on \(h\) i.e. \(H_0 = 100 h \; \mathrm{km} / \mathrm{s} / \mathrm{Mpc}\)
Hubble constant
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
\(\theta_\ast\) CMB angular acoustic scale
- Consistency with SDSS
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
- Consistency with SDSS
- In agreement with CMB
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
- Consistency with SDSS
- In agreement with CMB
- In \(3.7 \sigma\) tension with SH0ES
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
DESI + CMB measurements favor a flat Universe
\Omega_\mathrm{K} = 0.0024 \pm 0.0016 \; \green{(\text{DESI} + \text{CMB})}
Spatial curvature
Dark Energy Equation of State
Dark Energy fluid, pressure \(p\), density \(\rho\)
Equation of State parameter \(w = p / \rho\)
Linked to the evolution of Dark Energy \(w(z) = -1 + \frac{1}{3}\frac{d \ln f_\mathrm{DE}(z)}{d \ln (1 + z)}\)
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
\Lambda
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
- Union3 Rubin, Aldering, Betoule et al. 2023
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
- Union3 Rubin, Aldering, Betoule et al. 2023
- DES-SN5YR DES Collaboration et al. 2024
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.3095 \pm 0.0065 & \mathbf{(2.1\%)} \\
w &= -0.997 \pm 0.025 & \mathbf{(2.5\%)}
\end{align*}}_{\textstyle \text{\color{orange}{DESI + CMB + Pantheon+}}}
Assuming a constant EoS, DESI BAO fully compatible with a cosmological constant...
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w = p / \rho\)
w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
\left.
\begin{align*}
w_{0} &= -0.55^{+0.39}_{-0.21} \\
w_{a} &< -1.32
\end{align*}
\right\rbrace {\text{\color{black}{DESI}}}
Dark Energy Equation of State
Varying EoS
\Lambda
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
Varying EoS
w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
Varying EoS
w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
Varying EoS
w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
Varying EoS
w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{
w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}
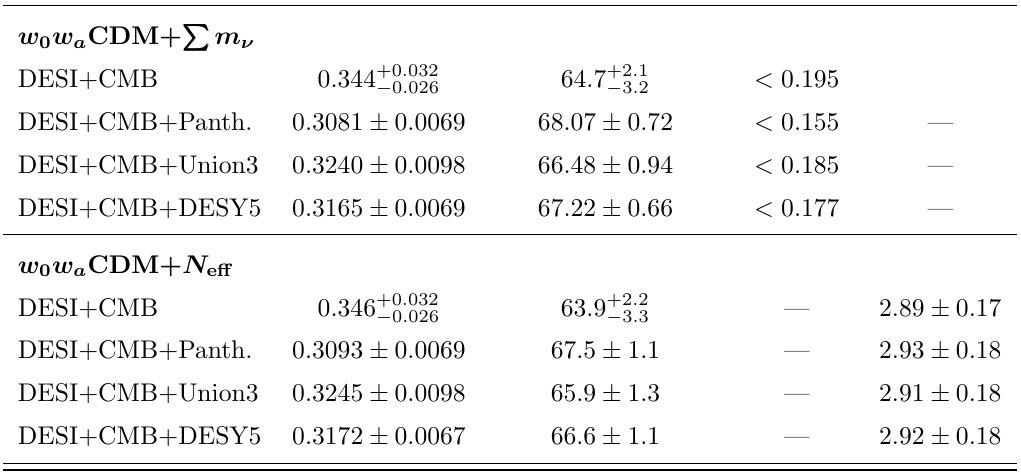
Dark Energy Equation of State
Combining all DESI + CMB + SN
\(w_{0} > -1, w_{a} < 0\) favored, level varying on the SN dataset
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{
w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}
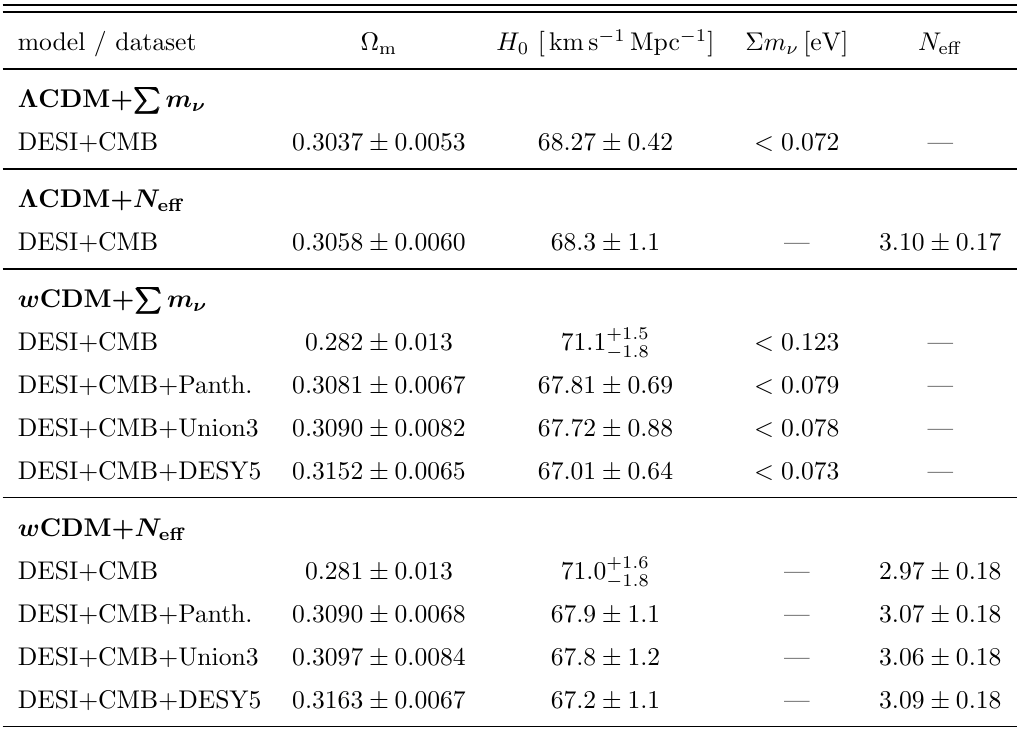
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO, especially through \(H_{0}\)
Low preferred value of \(H_{0}\) yields
\(\sum m_\nu < 0.072 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}\)
Limit relaxed for extensions to \(\Lambda\mathrm{CDM}\)
\(\sum m_\nu < 0.195 \, \mathrm{eV}\) for \(w_0w_a\mathrm{CDM}\)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
With \(> 0.1 \, \mathrm{eV}\) prior (IH)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
With \(> 0.1 \, \mathrm{eV}\) prior (IH)
Current constraints do not strongly favor normal over inverted hierarchy (\(\simeq 2 \sigma\))
Summary
DESI already has the most precise BAO measurements ever
Summary
DESI already has the most precise BAO measurements ever
DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM
Summary
DESI already has the most precise BAO measurements ever
DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM
In flat ΛCDM, DESI prefers "small \(\Omega_\mathrm{m}\), large \(H_0\) (though \(3.7\sigma\) away from SH0ES), small \(\sum m_\nu\)"
Summary
DESI already has the most precise BAO measurements ever
DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM
In flat ΛCDM, DESI prefers "small \(\Omega_\mathrm{m}\), large \(H_0\) (though \(3.7\sigma\) away from SH0ES), small \(\sum m_\nu\)"
Some hint of time-varying Dark Energy equation of state especially when combined with supernovae measurements
What's next?
"Full shape" (not only BAO peak measurement) analysis
Y3 data on disk!
The Pipeline
All codes public
- target selection, telescope operation, spectro reduction, redshift mesurement: https://github.com/desihub
- key analyses, BAO and Full Shape: https://github.com/cosmodesi
The Pipeline
All codes public
- target selection, telescope operation, spectro reduction, redshift mesurement: https://github.com/desihub
- key analyses, BAO and Full Shape: https://github.com/cosmodesi
desilike
- BAO, full shape likelihoods, designed to extend to other observables (lensing, etc.)
- wraps PT codes: velocileptors, pybird, folps(ax)
- automated cobaya / cosmosis / montepython bindings
- wraps samplers, profilers, fisher, in-place emulation
- "JAXification"
template = DirectPowerSpectrumTemplate(z=1.)
theory = LPTVelocileptorsTracerPowerSpectrumMultipoles(ells=(0, 2, 4), template=template)
theory(h=0.7, b1p=1.2) # returns pk
observable = TracerPowerSpectrumMultipoles(data=data, wmatrix=wmatrix, theory=theory,
klim={0: (0.02, 0.2), 2: (0.02, 0.2)})
likelihood = ObservablesGaussianLikelihood(observables=observable)
likelihood(Omega_m=0.3) # returns log-posterior
Other datasets
- SDSS BAO (for comparisons only): eBOSS Collaboration, 2020
- Primary CMB: Planck Collaboration, 2018
- CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
- BBN: Schöneberg et al., 2024
- SN: Pantheon+ Brout, Scolnic, Popovic et al., 2022, Union3 Rubin, Aldering, Betoule et al. 2023, DES-SN5YR DES Collaboration
\(\sum m_\nu\)
credit: Christophe Yèche
\(w(z)\)
DESI - SDSS consistency (\(\Omega_\mathrm{m}\))
Perfectly consistent!
Using these 2 points alone moves \(\Omega_\mathrm{m}\) by \(< 2 \sigma\)
Are SN \(\Omega_\mathrm{m}\) consistent?
Not so much in flat \(\Lambda\mathrm{CDM}\)...
(so we do not combine them in this model!)
Are SN \(\Omega_\mathrm{m}\) consistent?
Consistent in \(w_0w_a\mathrm{CDM}\)!
plik vs PR4 Planck likelihoods
Appendix B
\(w_0 - w_a\) with \(\sum m_\nu\) free
\(w_0 - w_a\) with \(\Omega_\mathrm{K}\)
Preference for \(w_{0} > -1, w_{a} < 0\) persists when curvature is left free
DE constraints driven by low-\(z\) ?
Not that much!
DESI + SDSS swaps DESI measurements with SDSS for \(z < 0.6\)
\(- 0.4 \sigma\) compared to DESI only
\(w(z)\)
Dark energy equation of state:
\(P = w \rho\)
- \(w\) = constant
BAO measurements: dark energy
BAO measurements: dark energy
Full tables
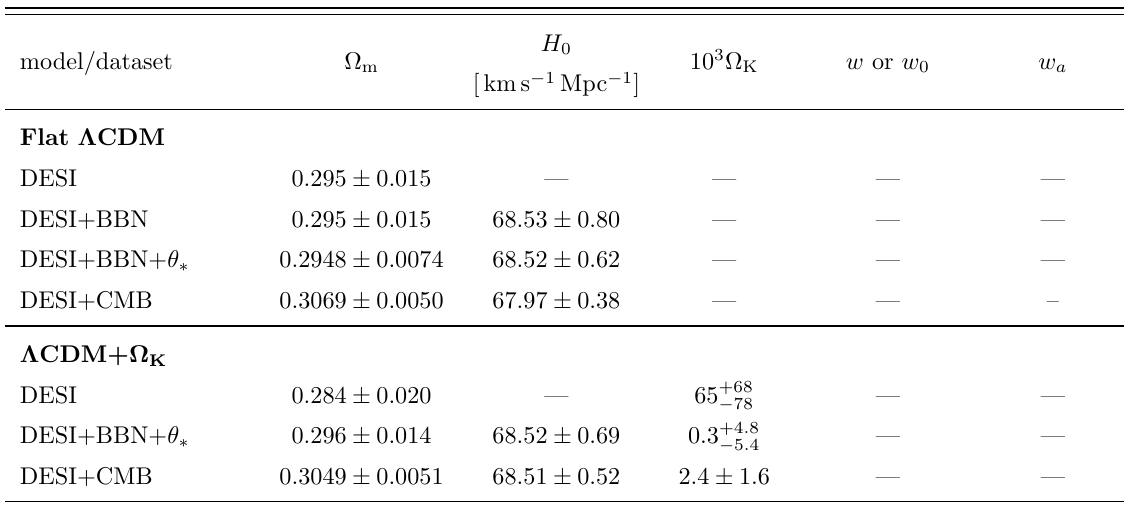
Full tables
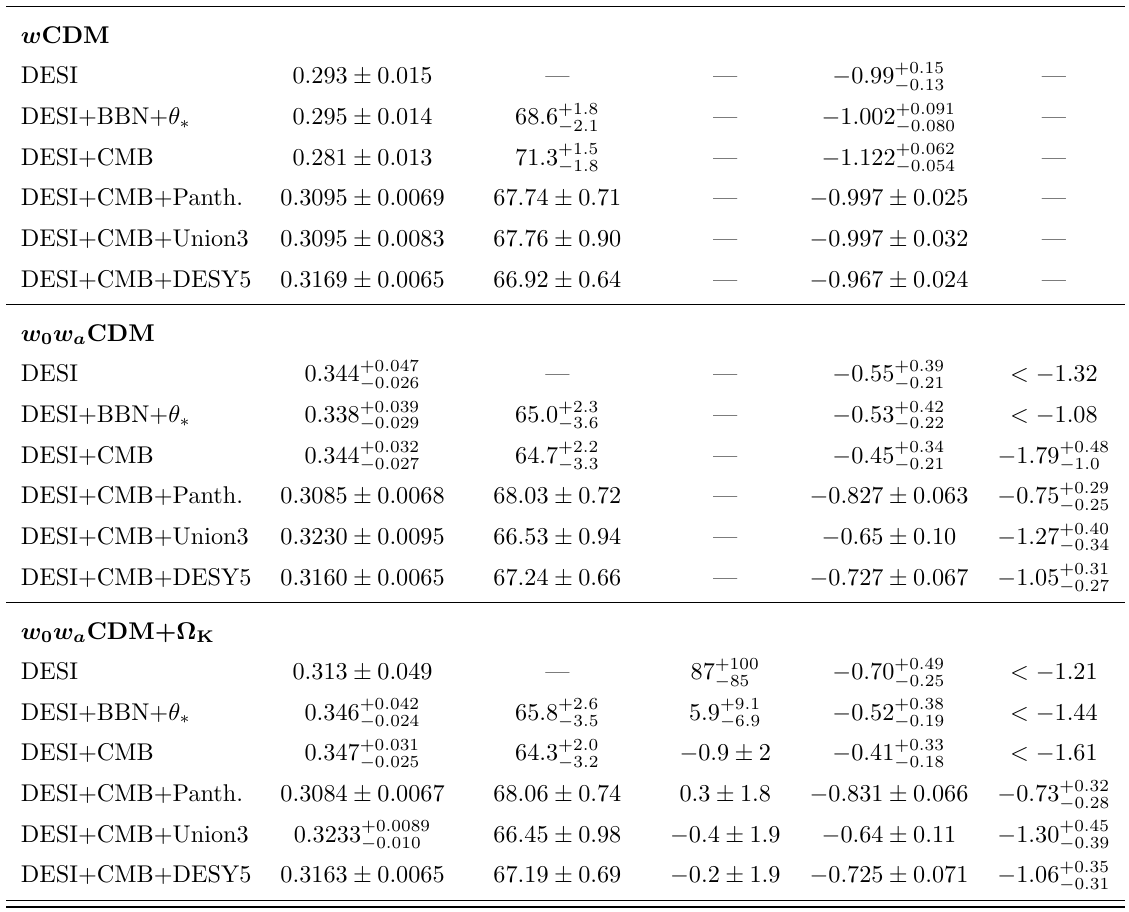
Full tables
Full tables
IRN_June2024
By Arnaud De Mattia
