DESI DR2 / DR1 vs Planck

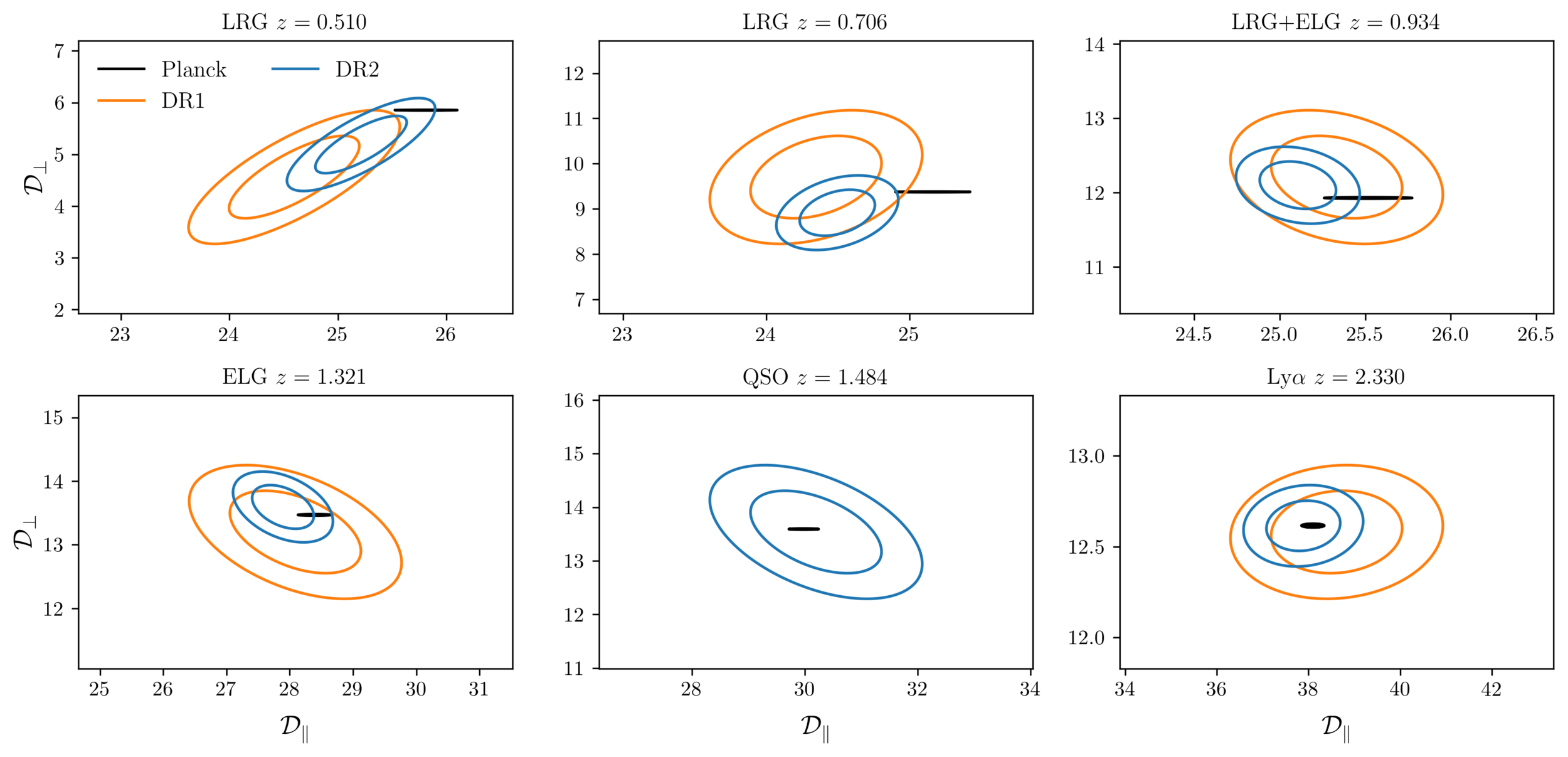
\(\mathcal{D}_\parallel, \mathcal{D}_\perp = \mathrm{Rot}(D_\mathrm{H}/r_\mathrm{d}, D_\mathrm{M}/r_\mathrm{d})\) with \(\mathcal{D}_\perp\) best constrained by Planck
following Efstathiou+25
DESI DR2 / DR1 vs Planck

turned into \(\omega_\mathrm{bc}\) constraint
DR2 more consistent
following Efstathiou+25
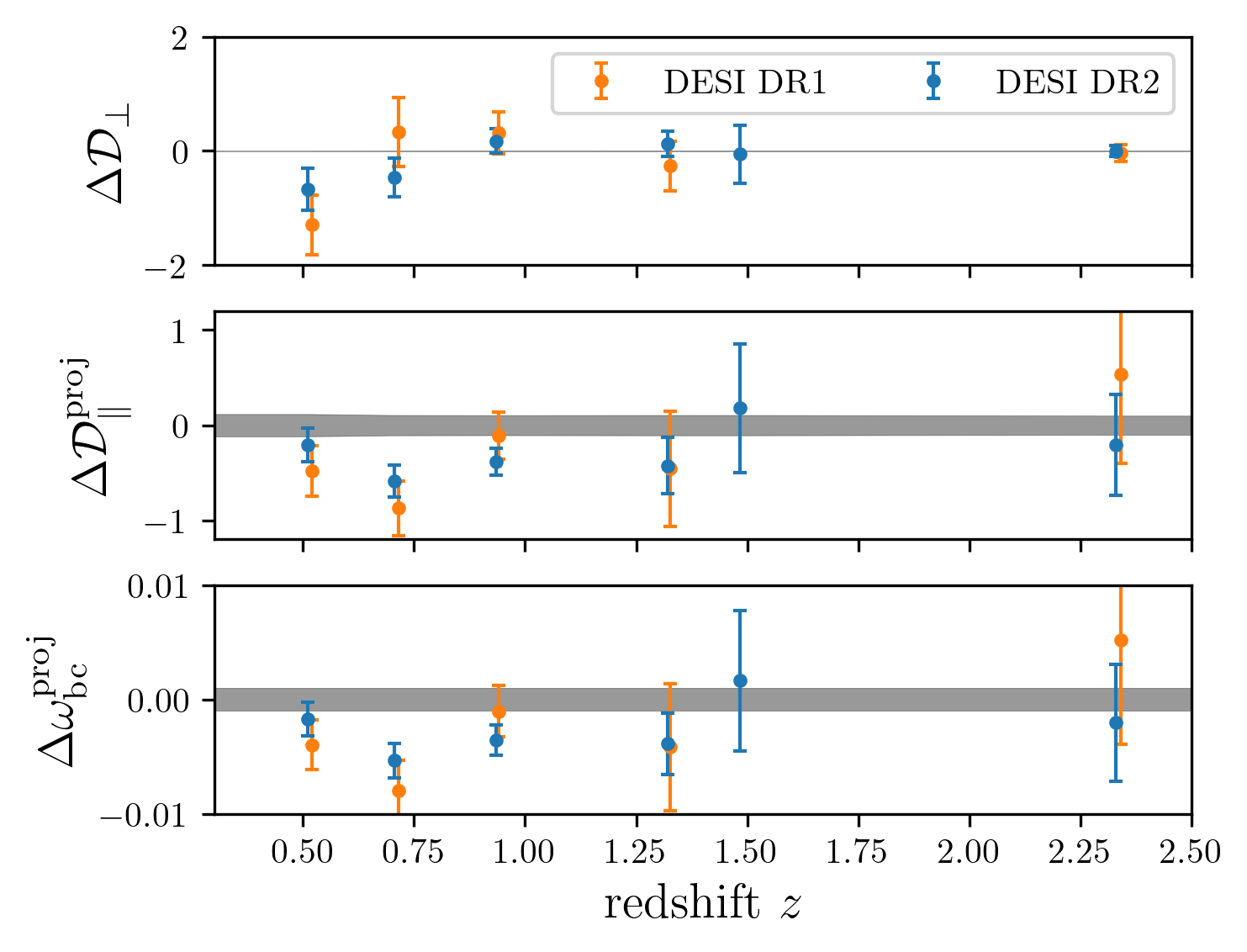
DESI DR2 / DR1 vs Planck

With CMB = low-\(\ell\) PR3 + CamSpec PR4 + (ACT+PR4) lensing
\(H_0r_d, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(2.3\sigma\)
\(2.2\sigma\)
\(2.2\sigma\)
\(1.8\sigma\)
\(1.9\sigma\)
\(2.1\sigma\)
\(0.8\sigma\)
\(2.6\sigma\)
\(2.7\sigma\)
\(1.3\sigma\)
\(2.1\sigma\)
\(2.3\sigma\)
no isotropic BAO
following Efstathiou+25
\(\mathcal{D}_\perp, \mathcal{D}_\parallel\) space
\(2.2\sigma\)
\(2.1\sigma\)
rotation
multiple counting of Planck uncertainty
DESI DR2 / DR1 vs Planck

\(H_0r_d, \Omega_\mathrm{m}\) space
BAO \(\alpha\) space
\(\mathcal{D}_\perp\)
\(\mathcal{D}_\parallel\)
\(\omega_\mathrm{bc}\)
DR2
DR1
\(1.9\sigma\)
\(1.9\sigma\)
\(1.9\sigma\)
\(1.6\sigma\)
\(1.7\sigma\)
\(2.0\sigma\)
\(0.8\sigma\)
\(2.2\sigma\)
\(2.3\sigma\)
\(1.3\sigma\)
\(1.9\sigma\)
\(2.1\sigma\)
no isotropic BAO
\(\mathcal{D}_\perp, \mathcal{D}_\parallel\) space
\(1.9\sigma\)
\(2.0\sigma\)
With CMB = low-\(\ell\) PR3 + CamSpec PR4
Apple-to-apple comparison

Combining with DESY5 SN?

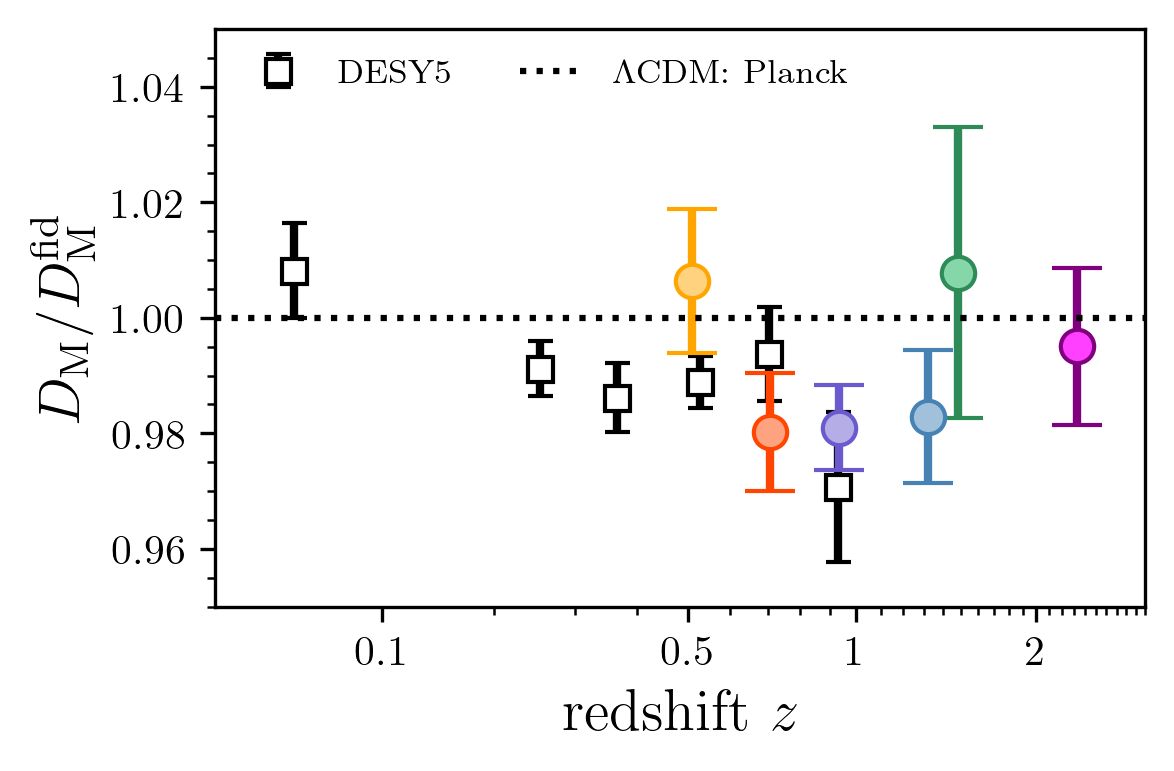
agreement between DESI BAO and DESY5 data at \(\sim 1.5\sigma\) level
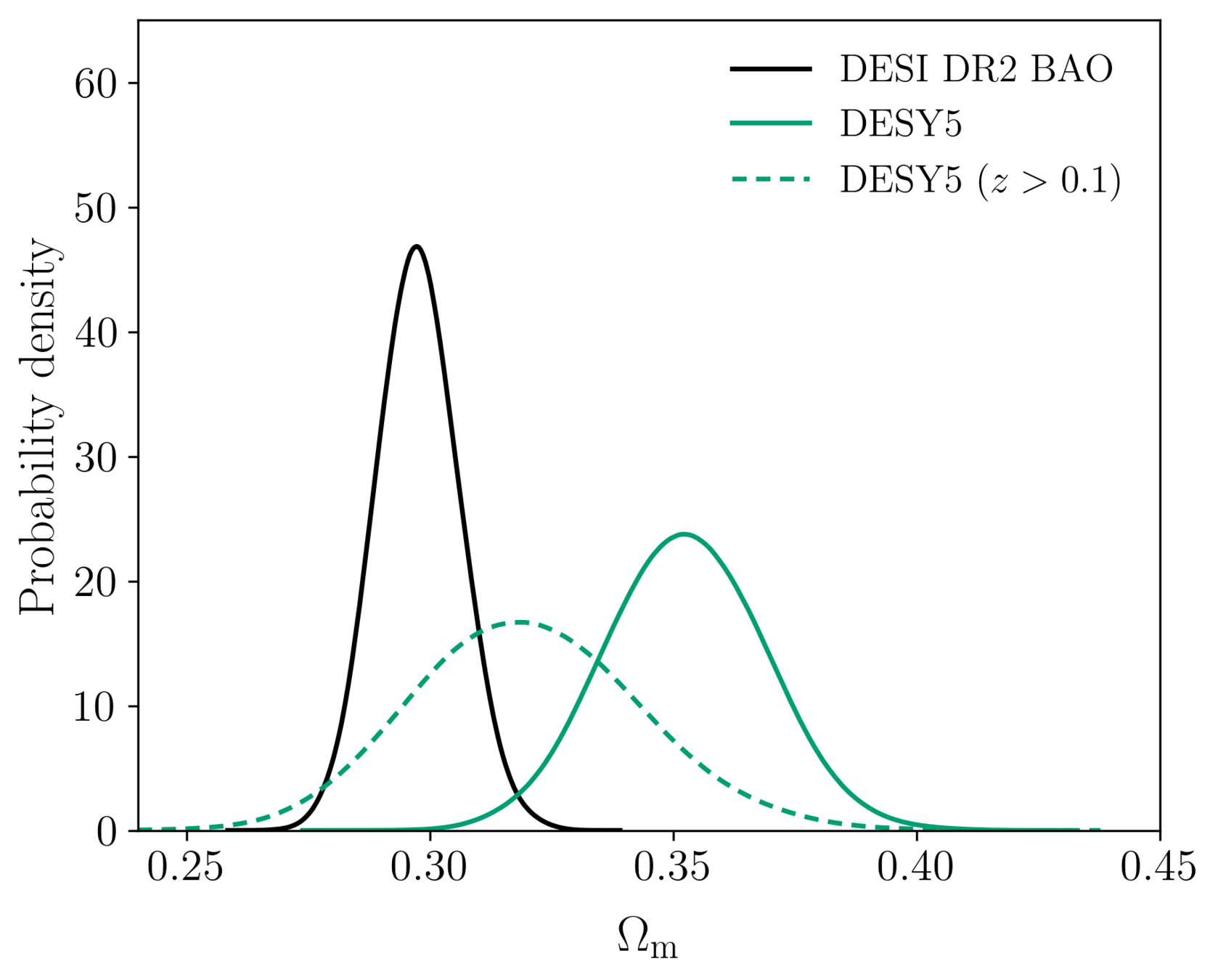
In the overlapping \(z\)-range, DESI DR2 BAO and DESY5 SN agree
\(\simeq 0.9 \sigma\)
Combining with DESY5 SN?

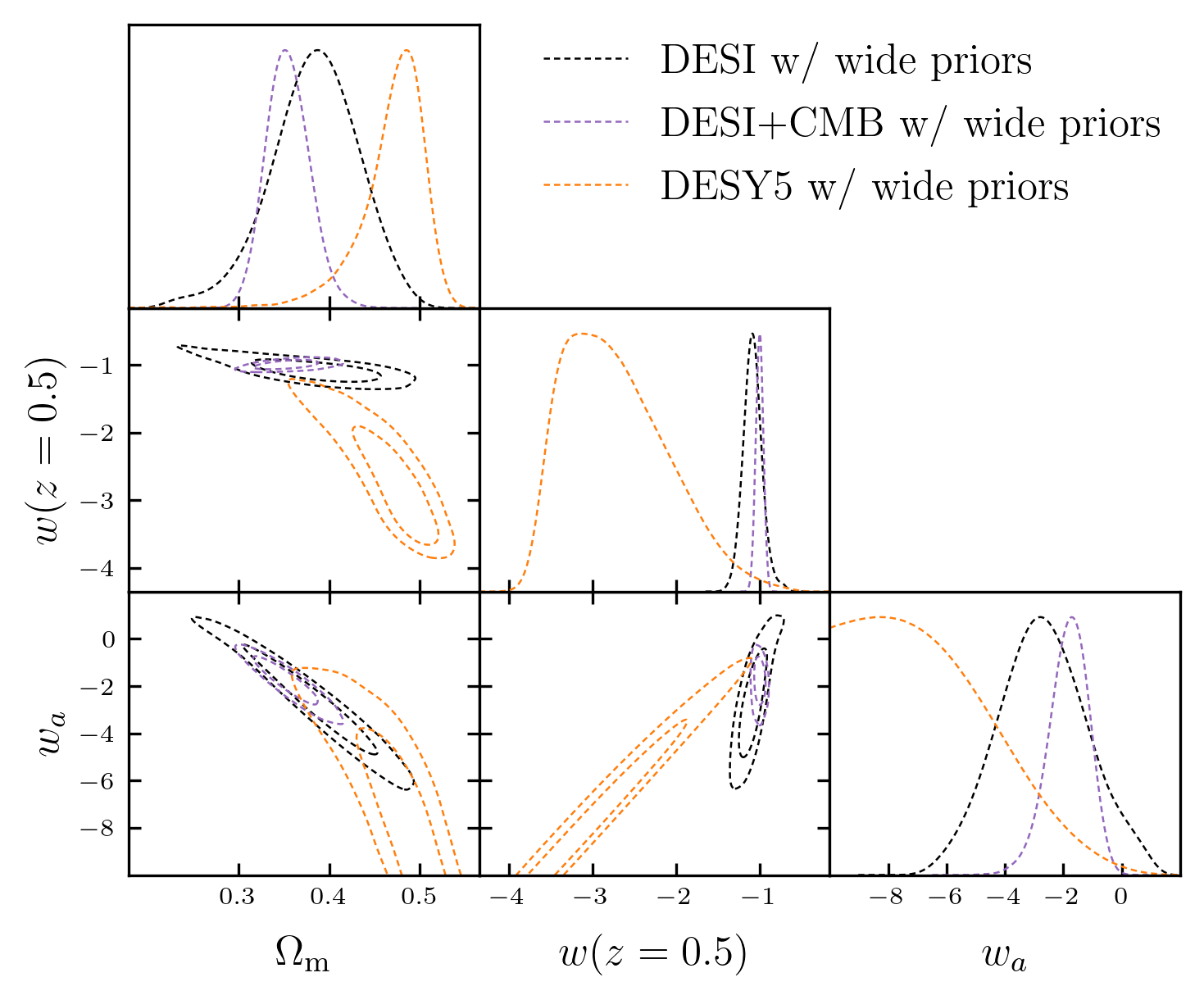
Combining with DESY5 SN?

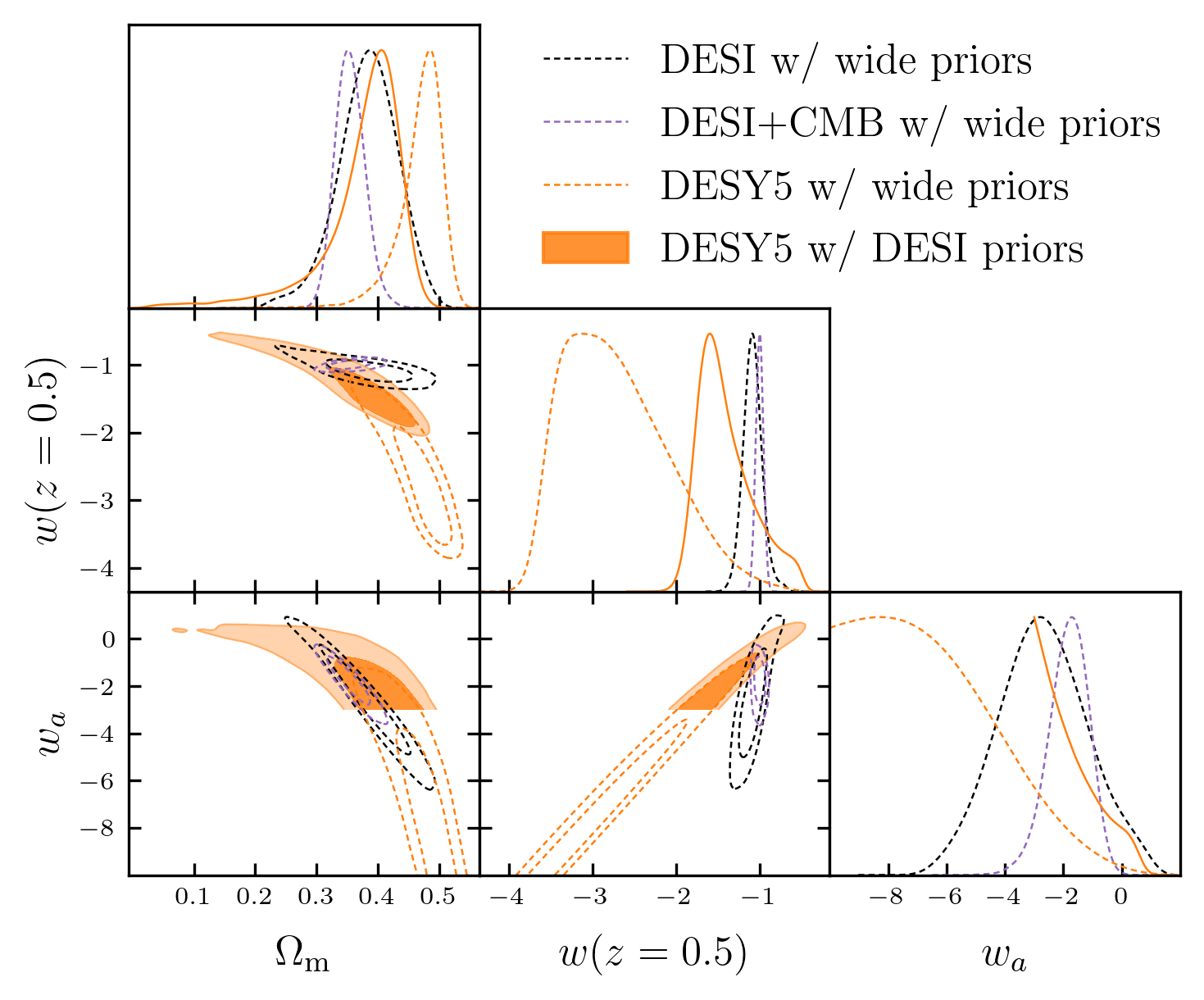
Combining with DESY5 SN?

\(\Delta \chi^2 \simeq 5.5\)
\(\chi^2_\mathrm{min} \simeq 1632, \mathrm{ndof} = 1829\)

Combining with DESY5 SN?

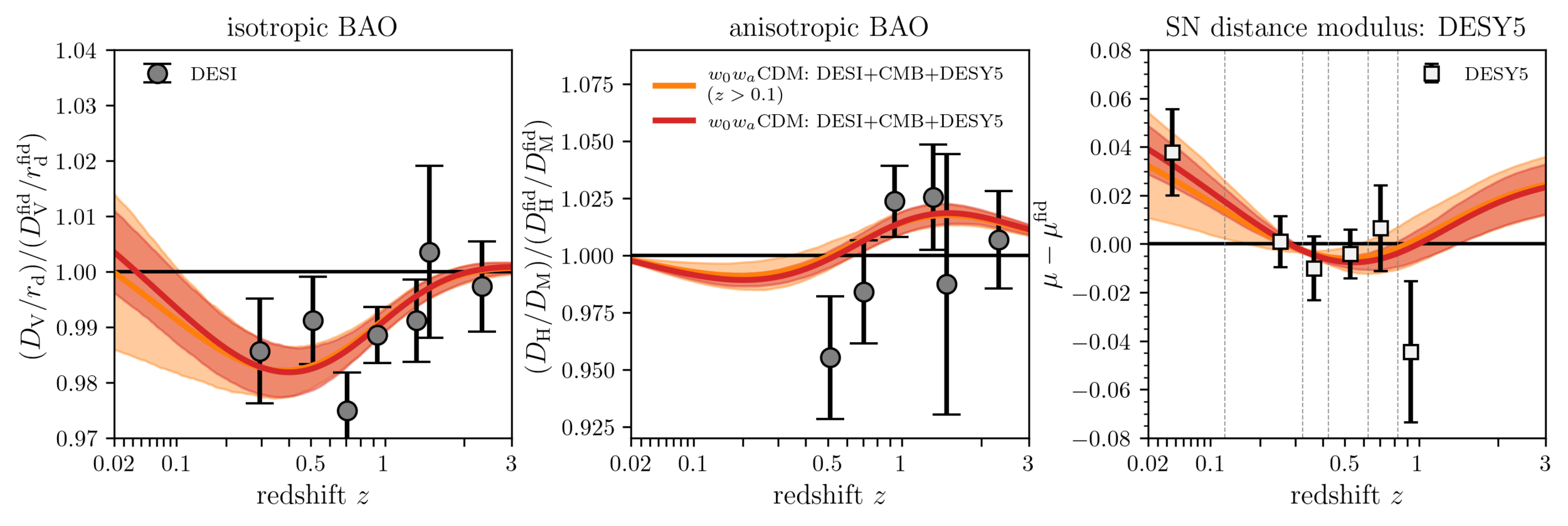
assuming \(z > 0.1\) fit, including the \(z < 0.1\) SN data
\(\Rightarrow\) \(\Delta \chi^2 = 186, \mathrm{ndof} = 197\)
full DESY5 best \(\chi^2\) barely changes between \(z > 0.1\) and full fit
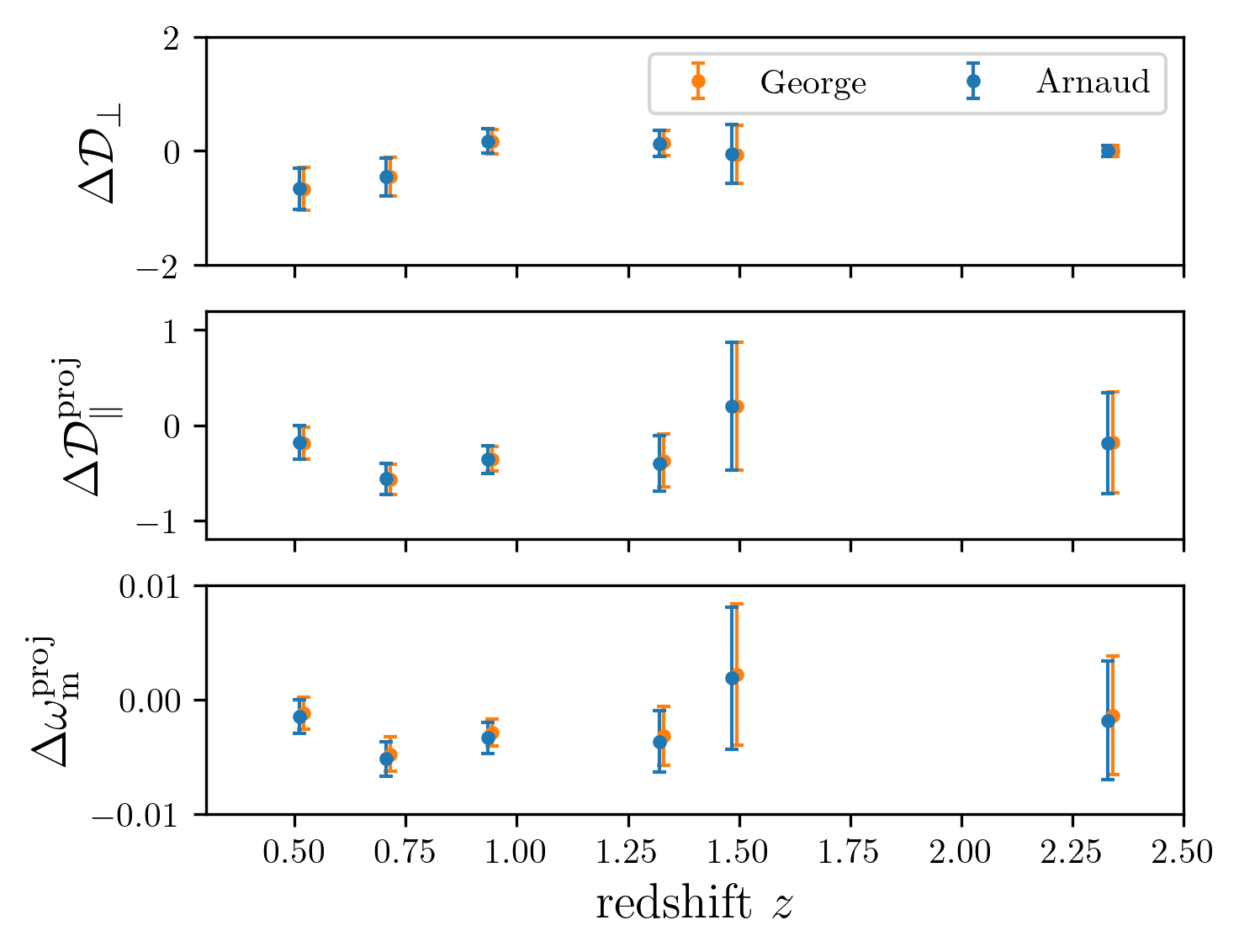
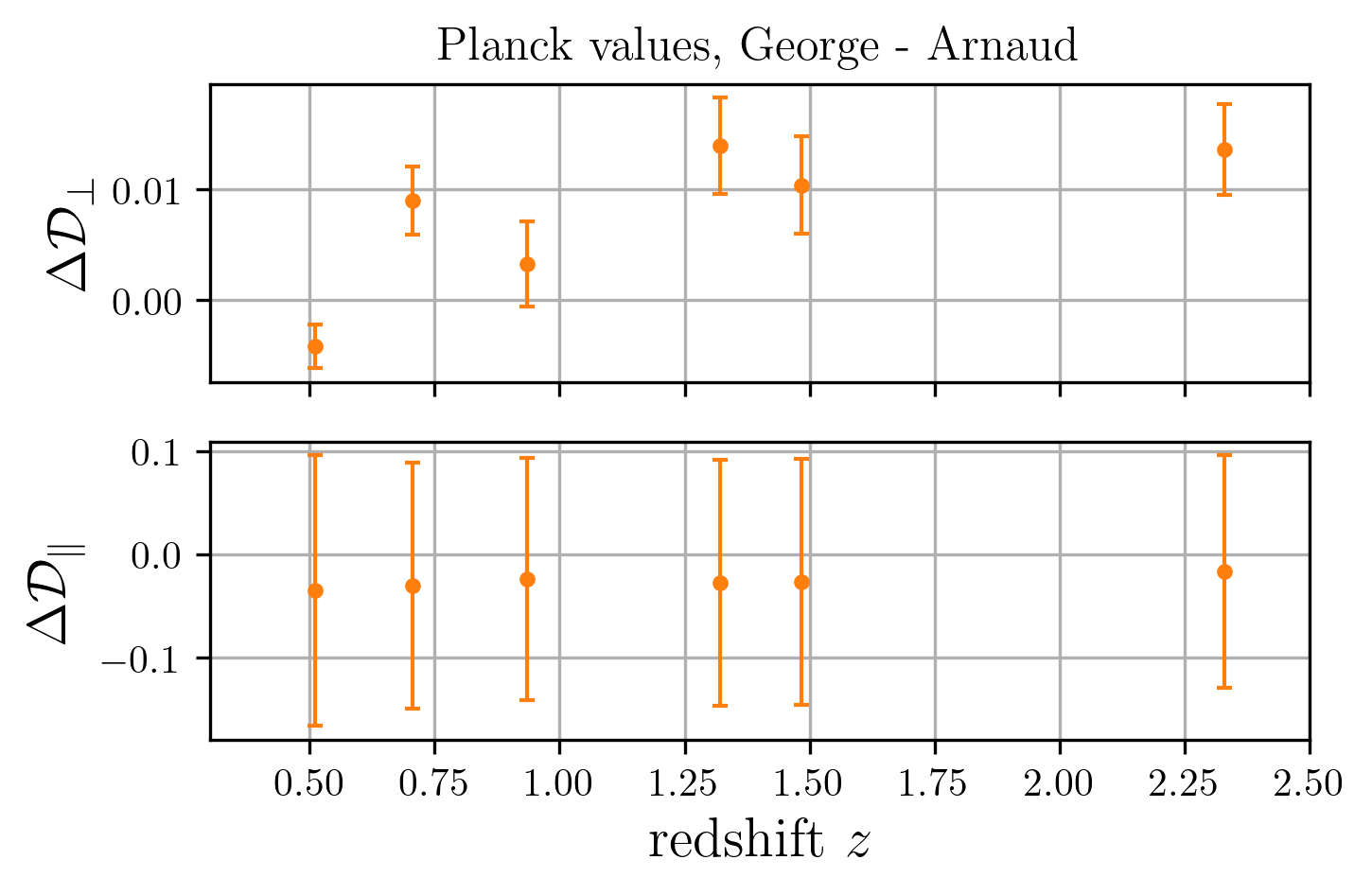
more_on_george_paper
By Arnaud De Mattia
more_on_george_paper
- 405


