• Top priority for AI: combinatorial generalisation.

"Humans’ capacity for combinatorial generalization depends critically on our cognitive mechanisms for representing structure and reasoning about relations"

Nature vs Nurture

• Previous eras: AI community focused on "nature", structured approaches.
• Modern deep learning: minimal "a priori" representation.
       Cheap data + Cheap computing resources

Challenges of deep learning

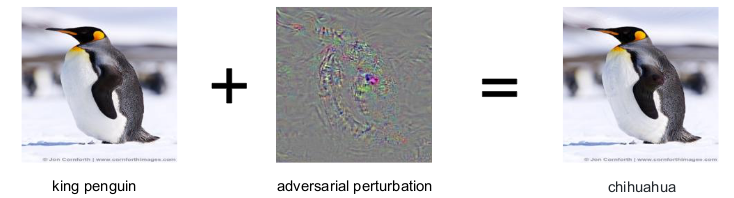
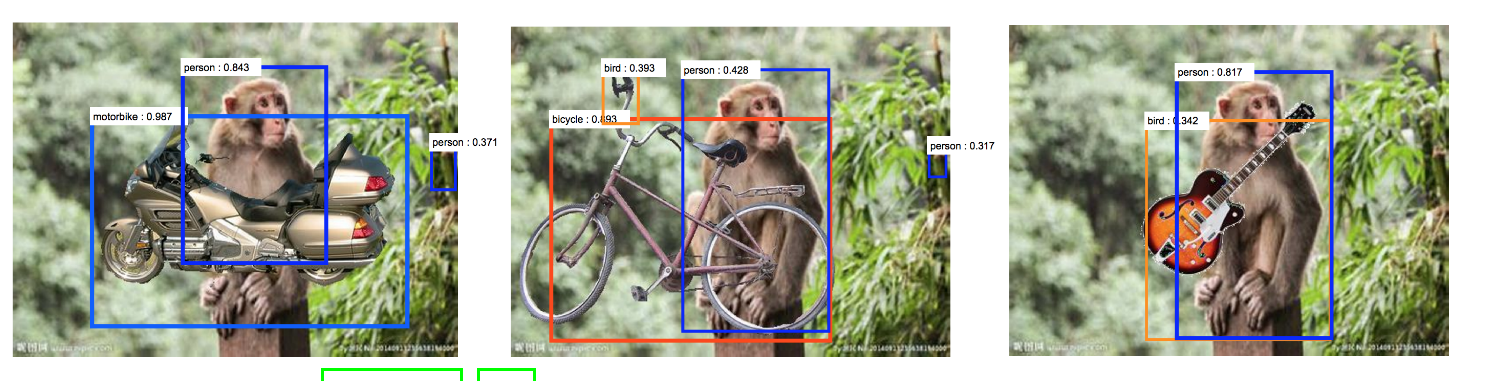
+ transfer learning, learning from small amounts of experience, etc.

A hybrid approach

• Need to go back at structured architectures.
• Capacity for performing calculations over discrete entities and their relations.

Relational reasoning

• Entity: element with attributes.
• Relation: property between entities.
• Rule: Function

Inductive biases

An inductive bias allows a learning algorithm to prioritize one solution over another, independent of the observed data.

Examples:

• Prior distribution
• Regularisation term
• Least-squares fitting
• etc.

Inductive biases on NN

What are the entities, what are the relations, and what are the rules for composing them, and their implications?

How can we impose arbitrary biases in our learning algorithm?

(centre of mass, N-body sim.)

Graphs

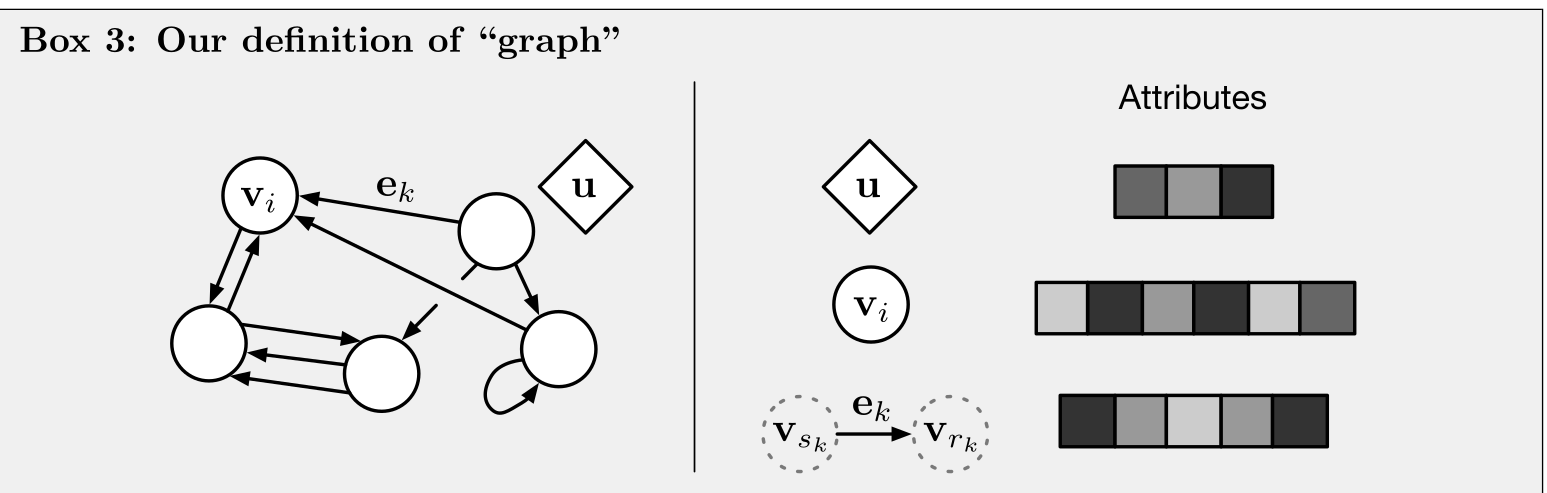
Graph networks

Graph neural networks have been extensively used successfully.

The "graph network (GN)" generalises and extends them, allowing to build complex architecture from simple blocks.

Example:

predicting the movement of rubber balls connected by springs in a gravitational field

• u: Gravitational field
• V: ball position, velocity, mass...
• E: springs

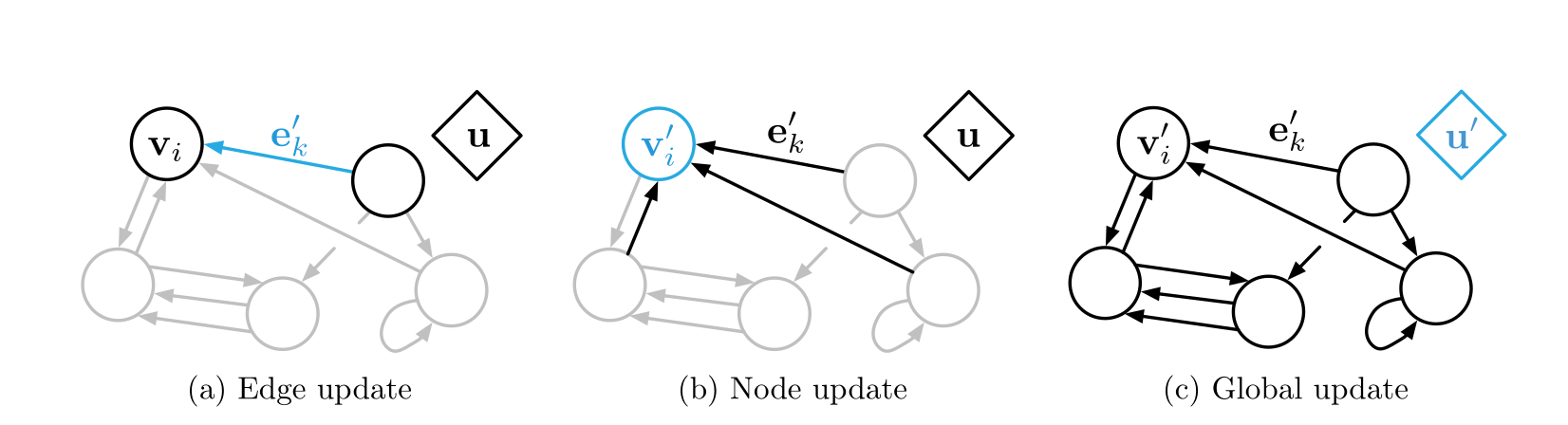
Relational inductive biases in graph networks

• We can express arbitrary relationships
• Invariant under permutations
• GN's per-edge and per-node functions are reused across all graph.
• A single GN can operate on graphs of different size and shape.

Design principles for graph network architectures

• The global, node, and edge attributes of a GN block can use arbitrary representational formats.
• Data may be naturally represented as a graph, or not.
• Multiblock architectures.

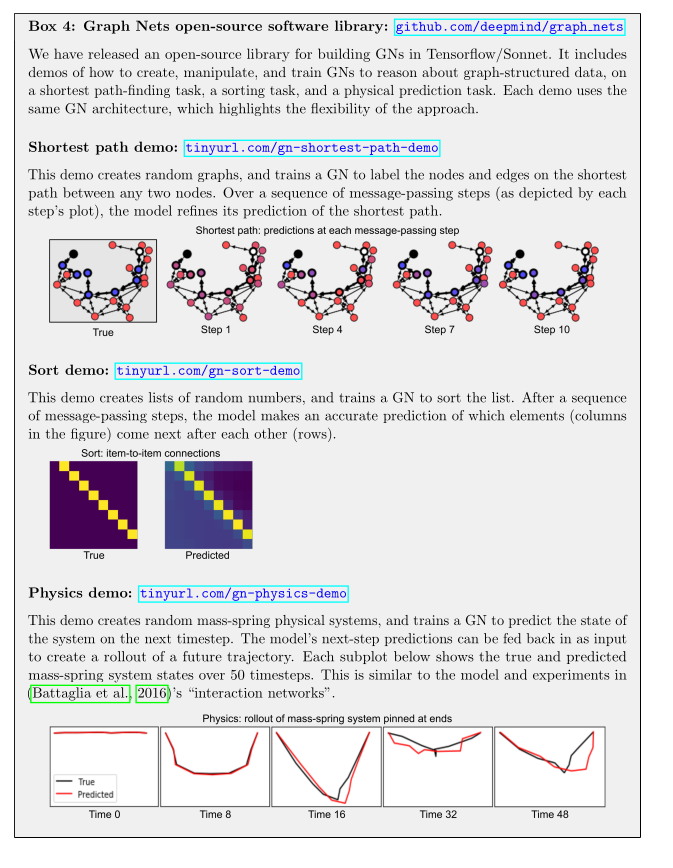
Conclusion

• A vast gap between human and machine intelligence remains, especially with respect to efficient, generalizable training.
• We explored flexible learning-based approaches which implement strong relational inductive biases.
• Graph Networks naturally support combinatorial generalisation and improve sample efficiency over other standard ML algorithms.