Convex Relaxation Techniques

On Community detection a.k.a Graph Clustering

What is a graph?

Edge or Connection

Vertex or Node

Our Problem: Finding communities in graphs

All possible combinations:

\mathcal{O}(2^n)
10^7

n= 20  more than

A generic clustering problem : 

 

\underset{x}{\text{min}}
s.t.
x_i = \{-1,1\}
f(x)

combinations

x \in \mathbb{R}^n

Relaxation a.k.a approximation

Difficult problem

Relaxed problem

Must hold:

\underset{x}{\text{min}}
s.t.
x_i = \{-1,1\}
f(x)
\underset{x}{\text{min}}
s.t.
-1 \leq x_i \leq 1
f(x)
\text{for}\ i=1,..n
\text{for}\ i=1,..n

Convex relaxation

In convex problems if optimal is found then is a global optimal

Community detection in many fields:

  • in biology finding groups of proteins with similar functionalities to explain biological processes
  • in social science to find groups that share traits.  e.g finding potential research collaborations
  • in political science to find groups with a similar ideology
  • in ecology to  find species
  • much more...

Graph theory 1: linear algebra representation

weighted edge

directed edge

self-loop

W := adjacency matrix

Example of adjacency matrix of a graph with communities

Graph theory 2: basic concepts

  • min-Distance: 
\delta(1,4)=2
\{v_1,v_3\}
\{v_2,v_3,v_4\}

Path-length 2:

Path-length 3:

 

  • Node-degree: nº of adjacent nodes 
d_3=3
d_4=1
  • Path: ordered set of edges that join two nodes

Graph theory 3: counting walks of length-2

(W^2)_{ij} = \sum_{k=1}^N w_{ik}w_{kj}
(W^2)_{25} = w_{21}w_{15}+w_{23}w_{35}+w_{22}w_{25}+w_{24}w_{45}+w_{25}w_{55}=2
(W^2)_{44} = w_{43}w_{34} = d_4 = 1

on undirected unweighted graphs

Graph theory 3: counting walks of length-n

(W^n)_{ij} = \sum_{k_1=1}^N \sum_{k_1=1}^N \sum_{k_{n-2}=1}^N \sum_{k_{n-1}=1}^N a_{i,k_1}a_{k_1,k_2}...a_{k_{n-2},k_{n-1}}a_{k_{n-1},j}
(W^3)_{25} = w_{23}w_{31}w_{15}+w_{21}w_{13}w_{35}=2

on undirected unweighted graphs

Graph theory 4: Centrality, Communicability and Betweenness

Which vertices/edges are important?

  • Centrality: Importance of a node

  • Communicability: well-connectedness between 2 nodes 

  • Betweenness: How much information flows through a node or edge

well-communicated

high centrality

high betweenness

Graph theory 4: Centrality, Communicability and Betweenness

  • Centrality node i: 

  • Communicability node i and j:  

  • Betweenness node r: 

f(W) = \sum_{n=1}^{\infty}c_nW^n

We can define in terms of walks

f(W)_{ii}
f(W)_{ij}
\frac{1}{(N-1)^2-(N-1)} {\sum\sum}_{i\neq j,j\neq r,\neq r}\frac{f(W)_{ij}-f(W-E(r))_{ij}}{f(W)_{ij}}

down-weighting parameter

walks of length n

Graph theory 4: Centrality, Communicability and Betweenness

f(W) = \Big(I + W + \frac{W^2}{2!} + ... + \frac{W^k}{k!} + ...\Big)
c_n = \frac{1}{n!}

Special case:

f(W) = e^W

Then..

Graph theory 5: the graph-Laplacian

L := D-W

Very nice properties:

x^TLx = \frac{1}{2}\sum_{i,j}^n w_{ij}(x_i-x_j)^2
  • For any vector                        :
x \in \mathbb{R}^n
  • L is symmetric positive semidefinite: 
x^TLx \geq 0
  •        is always a eigenvector with eigenvalue 0:
\overrightarrow{1}
\overrightarrow{1}L = 0

Back to our problem: Community detection

In terms of the graph-Laplacian

have trivial solution

 

We have to introduce a balancing constraint

but it becomes difficult to solve...

Spectral Relaxation

Expanded feasible set for 

but still, non-convex...

\mathbb{R}^2

Why is this non-convex relaxation good?

Eigendecomposition and               : 

From properties of L:   

\overrightarrow{1}L = 0

The second eigenvector is the solution for the relaxed problem!

Orthogonal matrix

Semidefinite relaxation (SDR)

change of variables 

\sum_{ij}w_{ij}x_ix_j = \sum_{ij}w_{ij}y_{ij} = \text{tr}(LY)

equivalent

relaxed problem

Convex problem!

Extracting solutions from SDR 1:

Low rank approximation + k-means

Low-rank approximation of Y

An optimal Y

Ordered spectrum of optimal Y

K-means with V rows as features

Extracting solutions from SDR 2: Randomization

X as a random variable

E[x] = 0

Stochastic Optimization Problem

equivalent to SDR

  1. Sample  
  2. Make                    e.g
  3. Reject unbalanced samples
  4. Evaluate in objective 
  5. Repeat from 1
x_i = \text{sgn}(y_i)
y
\zeta \sim \mathbb{N}(0,Y)

Augmented Adjacency Matrix 1: the idea

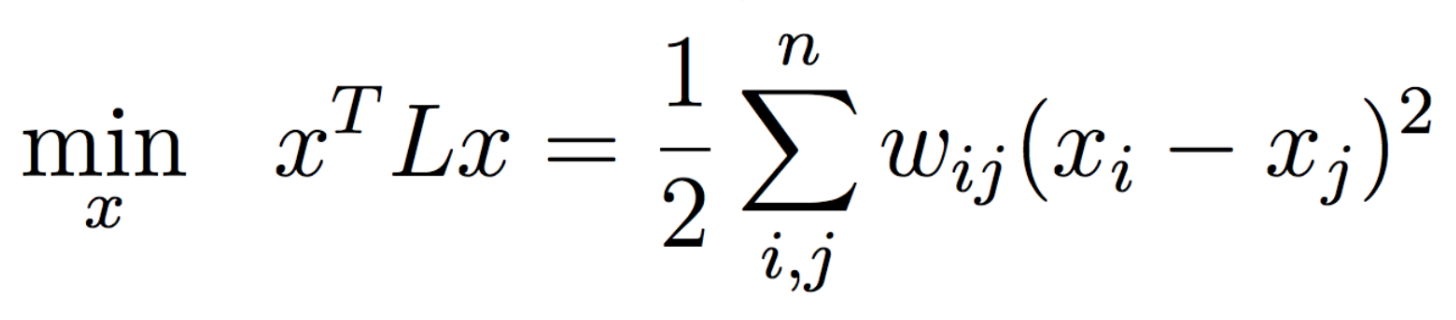
Recall

should :

  • Encourage pairing together alike nodes
  • Discourage pairing together dissimilar nodes
w_{ij}

e.g

W:=
w_{ij}=1 \quad \text{if} \ i \ and \ j \ connected
w_{ij}=0 \quad otherwise

Augmented adjacency matrix 2: Communicability

C:=
c_{ij}=high \quad \text{if} \ i \ and \ j \ \text{well-connected}
c_{ij}=low \quad otherwise
C = f(W) = \sum_{n=1}^{\infty}c_nW^n

Augmented adjacency matrix 3: Distance

D =
W =
S = W - D

Synthetic data: Stochastic Block Model (SBM)

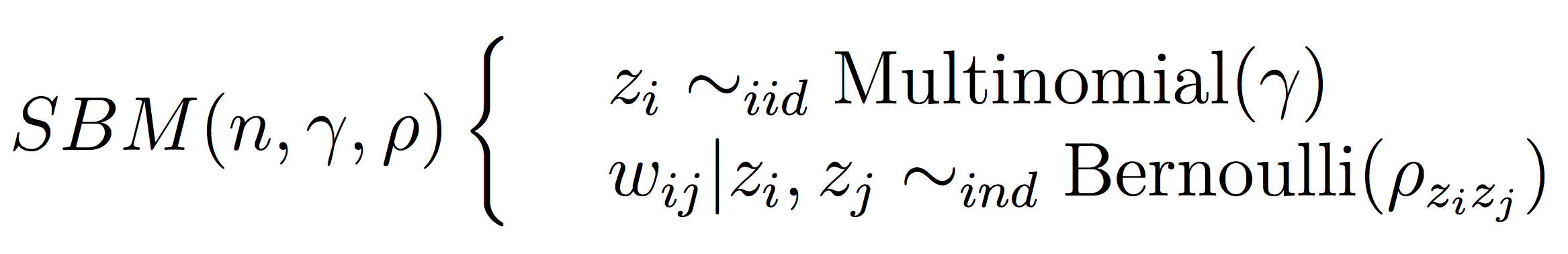
Synthetic Data: degree-corrected(DC) -SBM

Results on synthetic data

Experiments on real datasets 

Zachary Karate club  

Bottlenose Dolphins network

Results on real datasets

Silhouette index:

Modularity:

Conclusions

  • SDP can approximate hard clustering problems making them computationally feasible while keeping high performance
  • Different definitions of the node connections can enhance separability. E.g: communicability, distance
  • Different metrics, lead to different partitions. There isn't universal definition of community.

sdp-programming

By Arturo Arranz

Made with Slides.com

sdp-programming

  • 153