What is Target?

perfect model

X

(data)

Y

(label or sth)

假設存在一個這樣的東西
(也就是X和Y有某種關係。)

perfect model

X

(data)

Y

(label or sth)

乾脆直接找完美模型？

perfect model

不，這件事一般來說不太可能。

perfect model

X

(data)

Y

(label or sth)

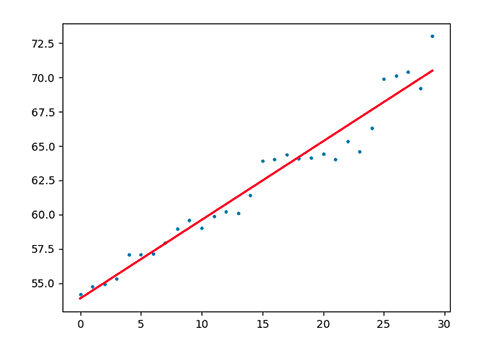
找出一個還可以的模型！

還行的model

Y'

(你預測的)

希望接近

Preface : Linear Regression

利用x找出y !

利用x,y 找出 z !

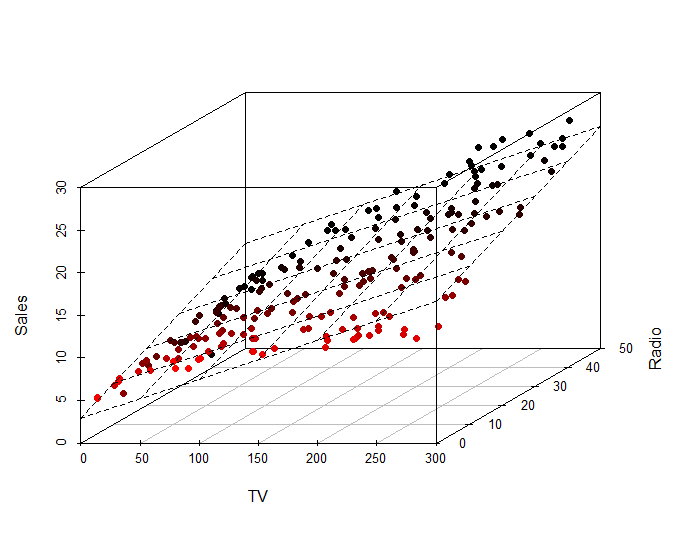
沒錯，有限維度都可以變成一個大X。

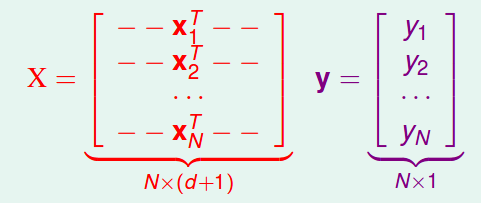
X(輸入資訊) @ w(回歸曲線) = y (實際值)

w: 學完的是參數

利用更新w的參數，把資料預測到完美。

perfect model

X

(data)

Y

(label or sth)

找出一個還可以的模型！

還行的model

Y'

(你預測的)

希望接近

（最小平方法）

X

(data)

深入model...

還行的model

Y'

(你預測的)

還行的model

演算法

(Algorithm)

參數θ

(Parameters)

線性回歸(lin reg)

學習出來的w線

大致上的兩步流程

1. model.fit

選擇一個方法，把資料丟給model去找出最佳算法。

model.fit

X-train

(data)

正在學θ
的model

Y-train

(你預測的)

想辦法做到最好！

2. model.predict

給定你想問的資料，把資料丟給model去找出最佳解答。

model.predict

X-train

學完θ
的model

Y-train

X-test

Y-test

Linear Regression(線性回歸)有公式，那有沒有沒有公式的演算法呢？

事實上，
有公式才是奇蹟！

那該如何得到好的θ？

Gradient Descent
(梯度下降法)

Gradient Descent
(梯度下降法)

Target 是什麼？

y和y'要長的像。

怎樣才叫做"像"？

L2_loss：(y-y')^2 越小越像。
L1_loss：|y-y'| 越小越像。
Likelihood (binary)：∏(y)(1-y')

"像"有什麼樣的特性？

損失函數(loss function) 很小。
通常這個時候微分接近零。

記得微積分取min的時候嘛？

Little Example

請找出 min x^2-x+5

奇怪？

微分=0不是有好幾種狀況嘛？

saddle point / min / max

Little Example 2

請找出
min (x-2)(x-1)(x+1)(x+2)

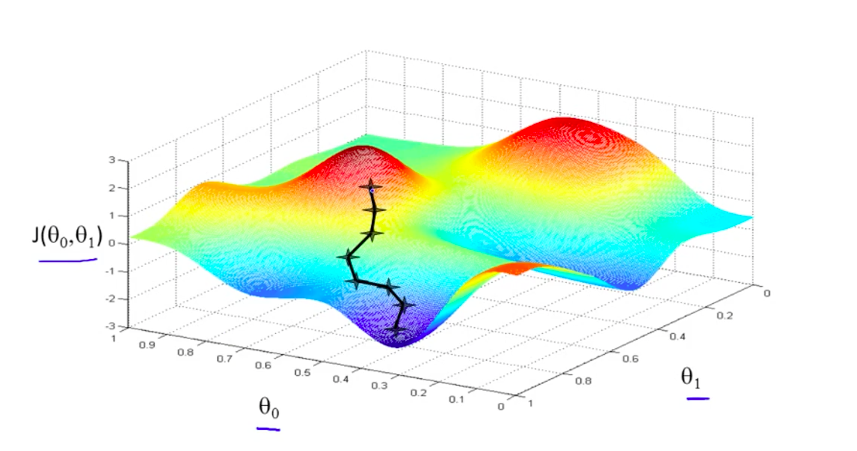
Little Example 3

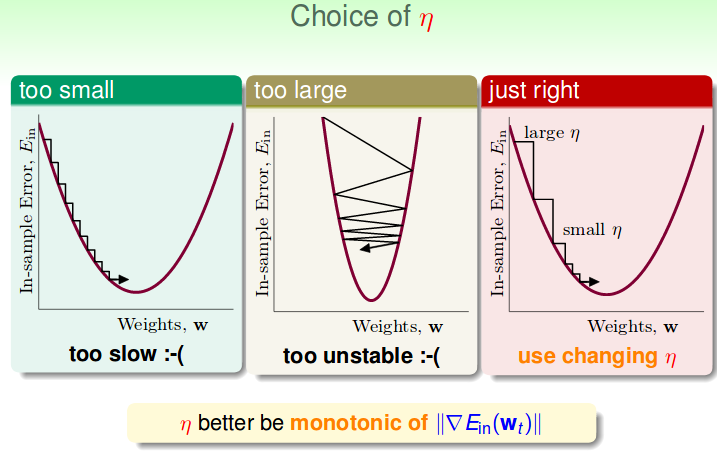
每次要走多大步？