Compressive sensing
(Oszczędne próbkowanie)
Emmanuel Candès, 2004 ($500k)
- by coincidence (Shepp–Logan phantom)
- l1 minimalization
- “It was as if you gave me the first three digits of a 10-digit bank account number — and then I was able to guess the next seven,”
So what and why?
Compressive sensing is a mathematical tool that creates hi-res data sets from lo-res samples.
It can be used to:
- resurrect old musical recordings,
- find enemy radio signals,
- and generate MRIs much more quickly.
Here’s how it would work with a photograph.

Undersample
Fill in the dots
(l1)
Add shapes
(sparsity)
Add smaller shapes
Achieve clarity
What is the key?
Compressive sensing
- magic of notion called sparsity
- pic made of solid blocks of color or wiggly lines is sparse,
- a screenful of random and chaotic dots is not
- out of all the bazillion possible reconstructions, the simplest, or sparsest, image is almost always the right one or very close to it
- how to find the sparsest image quickly?
Candès and Tao have shown mathematically that
the l1 minimization is all we need
R example
library(R1magic)
N <- 100
# Sparse components
K <- 4
# Up to Measurements > K LOG (N/K)
M <- 40
# Measurement Matrix (Random Sampling Sampling)
phi <- GaussianMatrix(N,M)
# R1magic generate random signal
xorg <- sparseSignal(N, K, nlev=1e-3)
y <- phi %*% xorg ;# generate measurement
T <- diag(N) ;# Do identity transform
p <- matrix(0, N, 1) ;# initial guess
# R1magic Convex Minimization
ll <- solveL1(phi, y, T, p)
x1 <- ll$estimate
plot( 1:100, seq(0.011,1.1,0.011), type = "n",xlab="",ylab="")
title(main="Random Sparse Signal Recovery",
xlab="Signal Component",ylab="Spike Value")
lines(1:100, xorg , col = "red")
lines(1:100, x1, col = "blue", cex = 1.5) 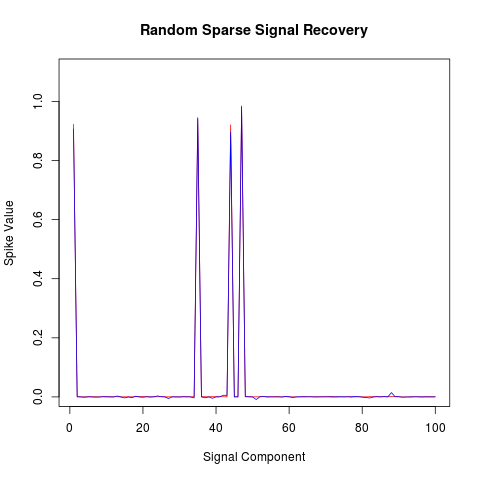
Bibliography
- http://www.wired.com/2010/02/ff_algorithm/all/1
- http://www.londonr.org/msuzen.pdf
- http://people.csail.mit.edu/indyk/princeton.pdf
Compressive sensing
By Bartosz Janota
Compressive sensing
- 70




