Week 2 Lab
Andrew Beam, PhD
Department of Epidemiology
Harvard T.H. Chan School of Public Health
twitter: @AndrewLBeam
In class assignment:
PERCEPTRON BY HAND
PERCEPTRONS
Let's say we'd like to have a single neural learn a simple function
y
X_1
X_2
| X1 | X2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
w_2
w_1
b
Observations
PERCEPTRONS
How do we make a prediction for each observations?
y
X_1
X_2
| X1 | X2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
w_2
w_1
b
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
Observations
Predictions
For the first observation:
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
X_1 = 0, X_2 = 0, y =0
Predictions
For the first observation:
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
X_1 = 0, X_2 = 0, y =0
First compute the weighted sum:
h = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + (-0.5)
h = -0.5
Predictions
For the first observation:
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
X_1 = 0, X_2 = 0, y =0
First compute the weighted sum:
h = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + -0.5
h = -0.5
Transform to probability:
p = \frac{1}{1+\exp(-h)}
p = \frac{1}{1+\exp(-0.5)}
p = 0.38
Predictions
For the first observation:
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
X_1 = 0, X_2 = 0, y =0
First compute the weighted sum:
h = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + -0.5
h = -0.5
Transform to probability:
p = \frac{1}{1+\exp(-h)}
p = \frac{1}{1+\exp(-0.5)}
p = 0.38
Round to get prediction:
\hat{y} = round(p)
\hat{y} = 0
Predictions
Putting it all together:
h = w_1*X_1 + w_2*X_2 + b
p = \frac{1}{1+\exp(-h)}
\hat{y} = round(p)
Assume we have the following values
| w1 | w2 | b |
|---|---|---|
| 1 | -1 | -0.5 |
| X1 | X2 | y | h | p | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -0.5 | 0.38 | 0 |
| 0 | 1 | 1 | -1.5 | 0.18 | 0 |
| 1 | 0 | 1 | 0.5 | .62 | 1 |
| 1 | 1 | 1 | -0.5 | 0.38 | 0 |
\hat{y}
Fill out this table
Room for Improvement
Let's define how we want to measure the network's performance.
There are many ways, but let's use squared-error:
(y - p)^2
Room for Improvement
Let's define how we want to measure the network's performance.
There are many ways, but let's use squared-error:
Now we need to find values for that make this error as small as possible
(y - p)^2
w_1, w_2, b
The Backpropagation Algorithm
h = w_1*X_1 + w_2*X_2 + b
p = \frac{1}{1+\exp(-h)}
Our perceptron performs the following computations
\ell = (y - p)^2
And we want to minimize this quantity
The Backpropagation Algorithm
h = w_1*X_1 + w_2*X_2 + b
p = \frac{1}{1+\exp(-h)}
Our perception performs the following computations
\ell = (y - p)^2
And we want to minimize this quantity
We'll compute the gradients for each parameter by "back-propagating" errors through each component of the network
The Backpropagation Algorithm
For we need to compute
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
w_1
\frac{\partial \ell}{\partial w_1}
\ell = (y - p)^2
To get there, we will use the chain rule
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
This is "backprop"
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = ?
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
\frac{\partial p}{\partial h} = ?
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
\frac{\partial p}{\partial h} = p*(1-p)
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
\frac{\partial p}{\partial h} = p*(1-p)
\frac{\partial h}{\partial w} = ?
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
\frac{\partial p}{\partial h} = p*(1-p)
\frac{\partial h}{\partial w_1} = X_1
The Backpropagation Algorithm
Let's break it into pieces
h = w_1*X_1 + w_2*X_2 + b
Computations
p = \frac{1}{1+\exp(-h)}
Loss
\ell = (y - p)^2
\frac{\partial \ell}{\partial w_1} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial h}*\frac{\partial h}{\partial w_1}
\frac{\partial \ell}{\partial p} = 2*(p-y)
\frac{\partial p}{\partial h} = p*(1-p)
\frac{\partial h}{\partial w_1} = X_1
\frac{\partial \ell}{\partial w_1} = 2*(p-y)*p*(1-p)*X_1
Putting it all together
Gradient Descent with Backprop
gw_1 = \eta*(p - y)*(p*(1-p)*X_1)
1) Compute the gradient for
w^{new}_1 = w^{old}_1 - \frac{1}{N}\sum gw_1
2) Update
w_1
w_1
\eta
is the learning rate
For some number of iterations we will:
3) Repeat until "convergence"
Learning Rules for each Parameter
gw_1 = (p - y)*(p*(1-p)*X_1)
gw_2 = (p - y)*(p*(1-p)*X_2)
g_b = (p - y)*(p*(1-p))
Gradient for
Gradient for
Gradient for
w^{new}_1 = w^{old}_1 - \eta*\frac{1}{N}\sum gw_1
Update for
Update for
Update for
w^{new}_2 = w^{old}_2 - \eta*\frac{1}{N}\sum gw_2
b^{new} = b^{old} - \eta*\frac{1}{N}\sum g_b
w_1
w_1
w_2
w_2
b
b
\eta
is the learning rate
IMPLEMENTATION IN PYTHON
GPUs
GPU COMPUTING
Training neural nets = large matrix multiplications
GPUs = Massively parallel linear algebra devices
Special computer chips known as graphics processing units (GPUs) make training huge models on large data tractable
GPUs vs. CPUs
CPUs
1000s of number crunchers
GPUs
General
Purpose
Computation
REGULARIZATION
REGULARIZATION
One of the biggest problems with neural networks is overfitting.
Regularization schemes combat overfitting in a variety of different ways
WHY DO WE NEED IT?
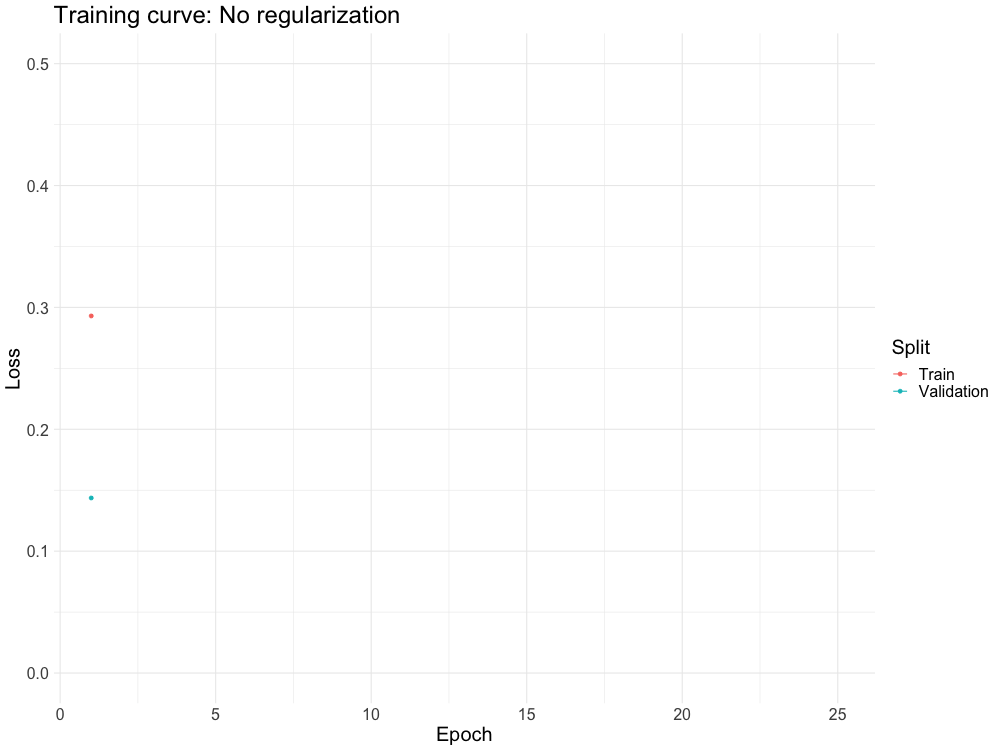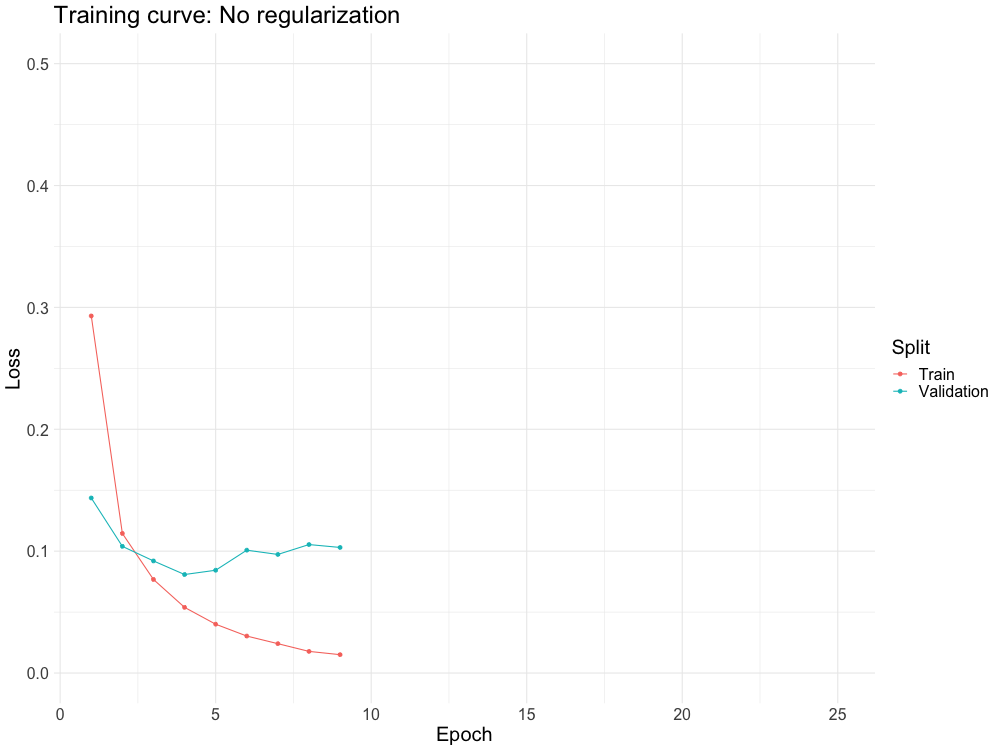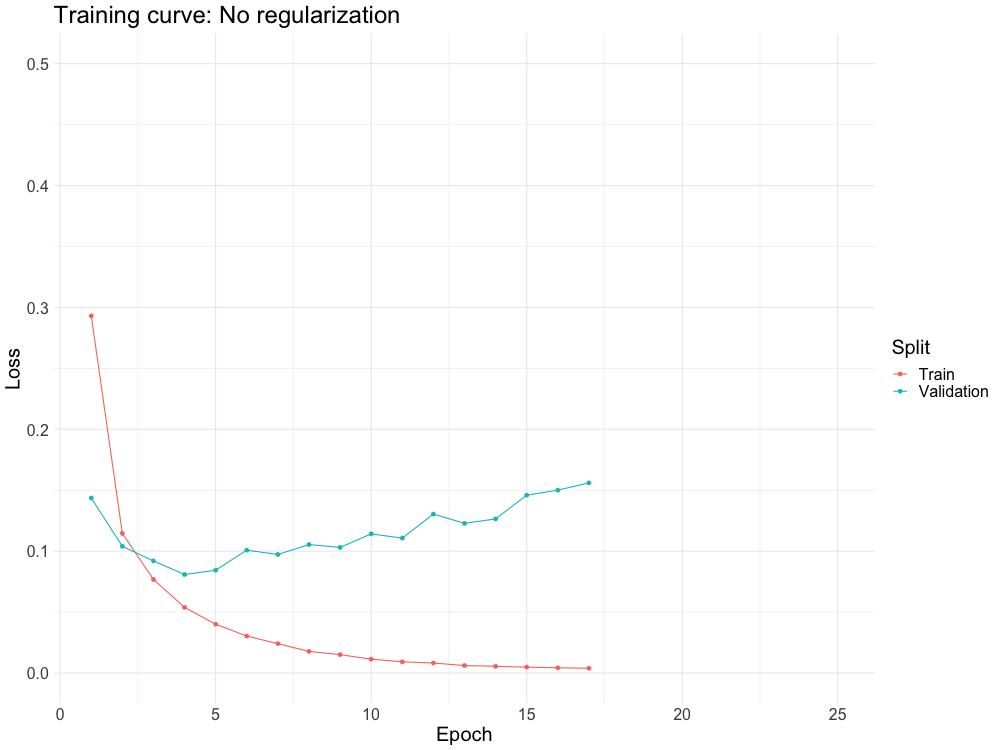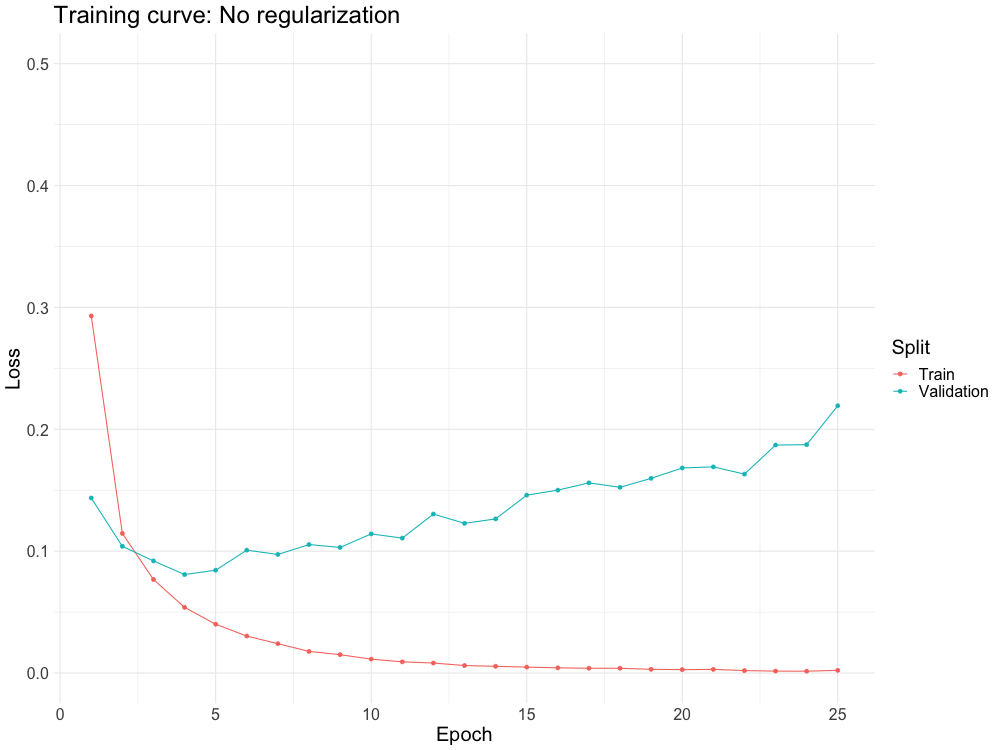
WHY DO WE NEED IT?
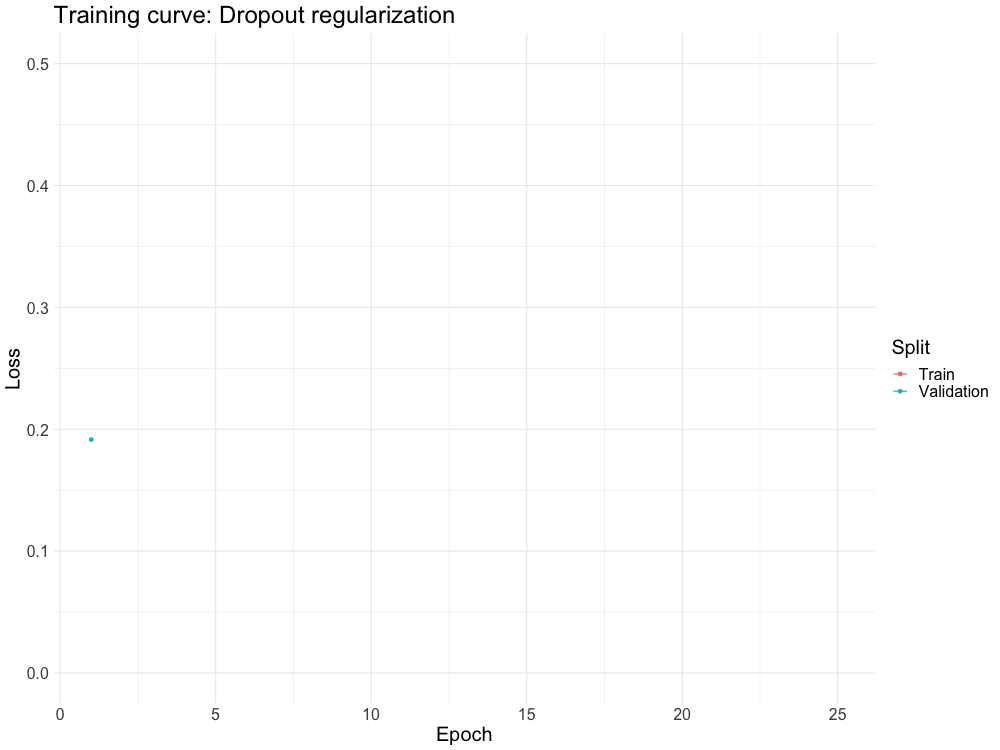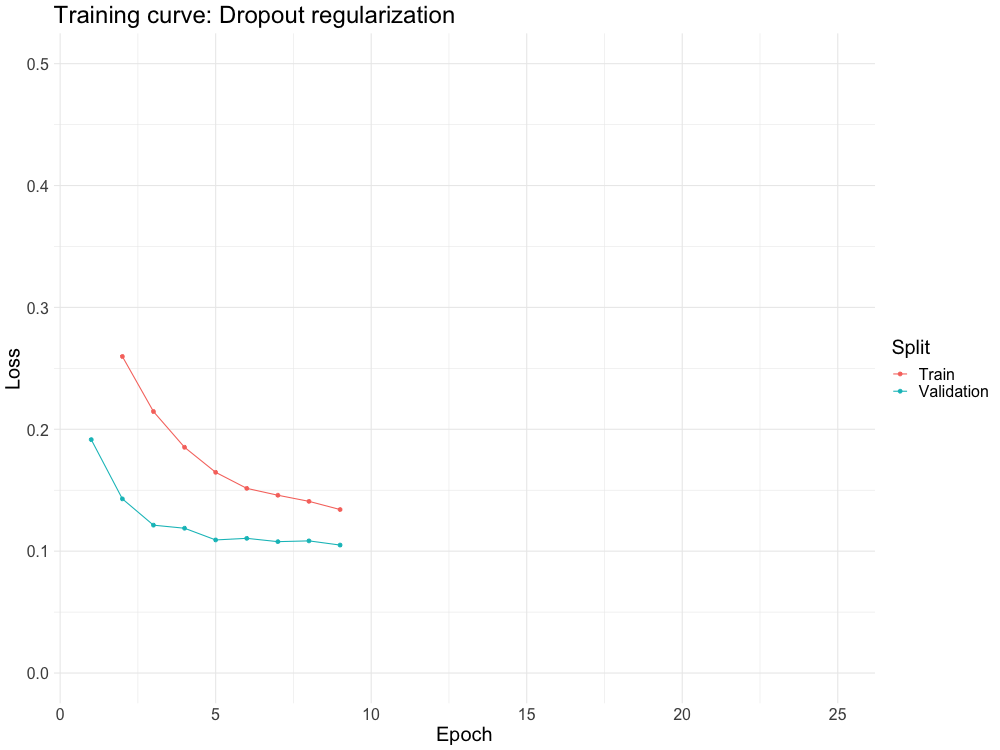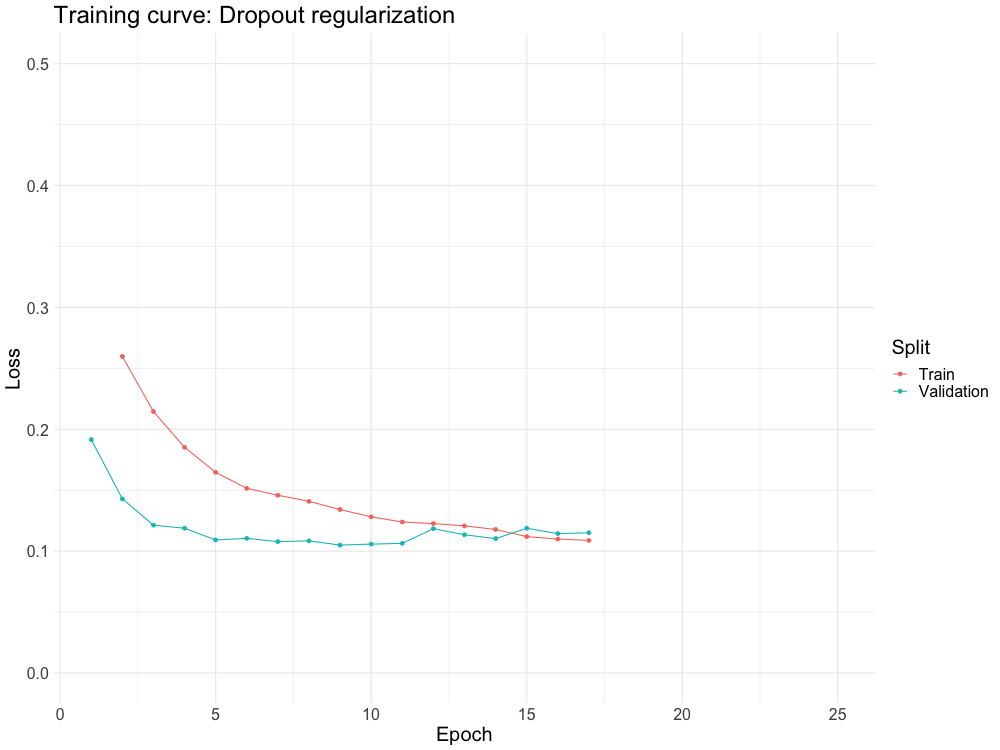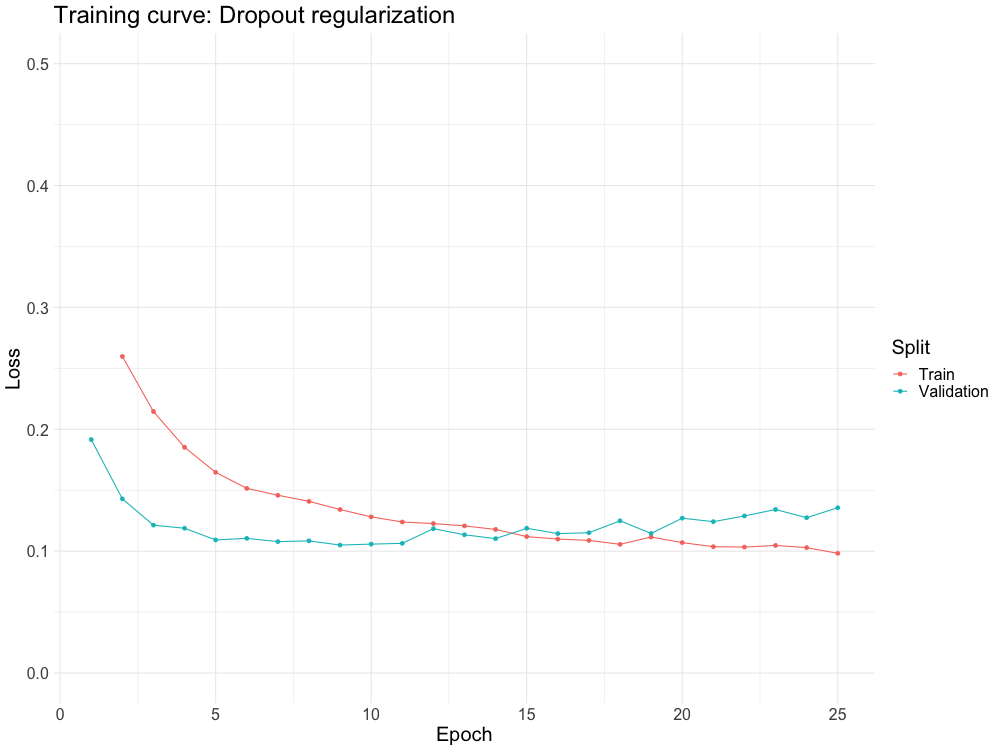
WHY DO WE NEED IT?
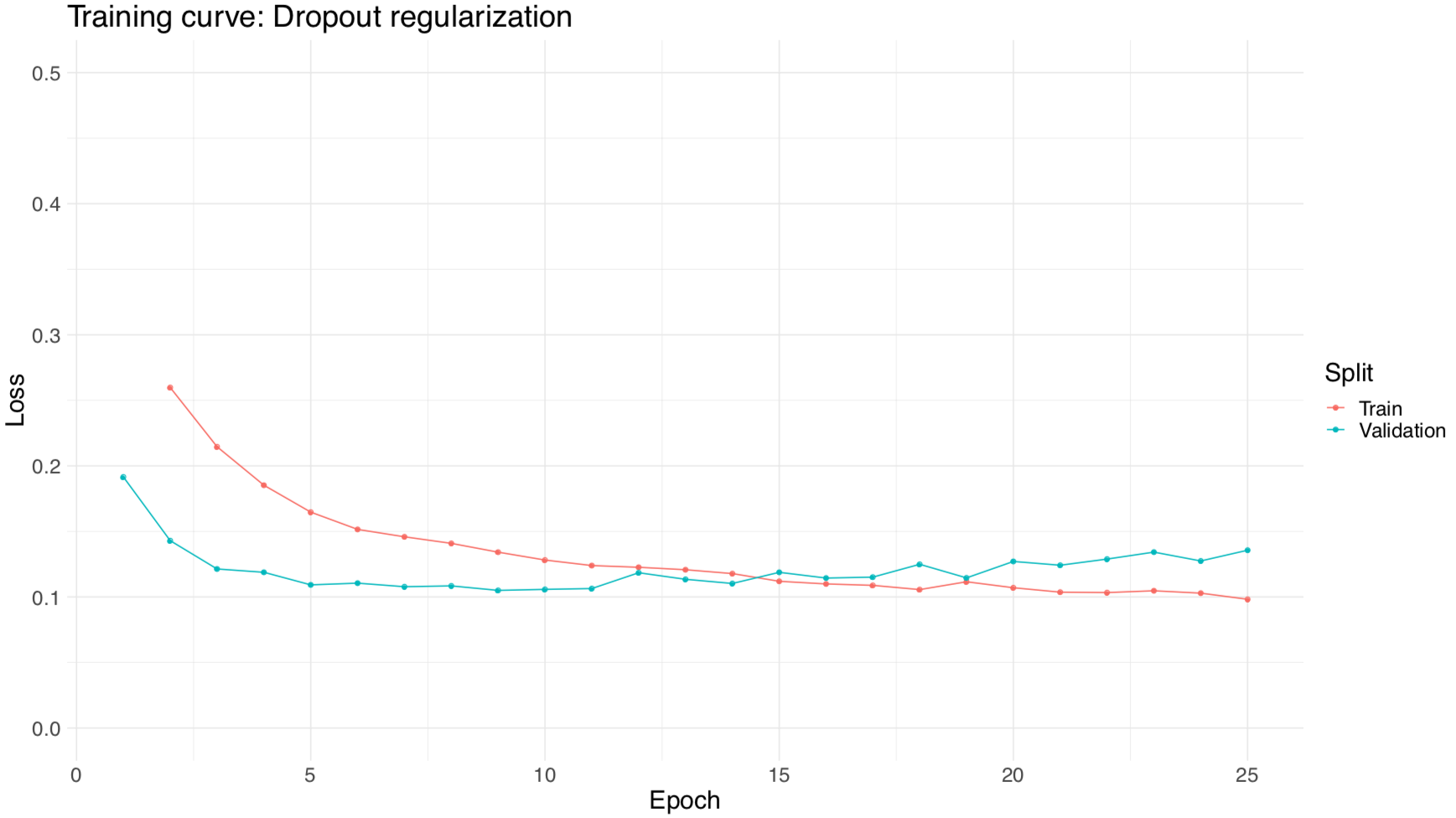
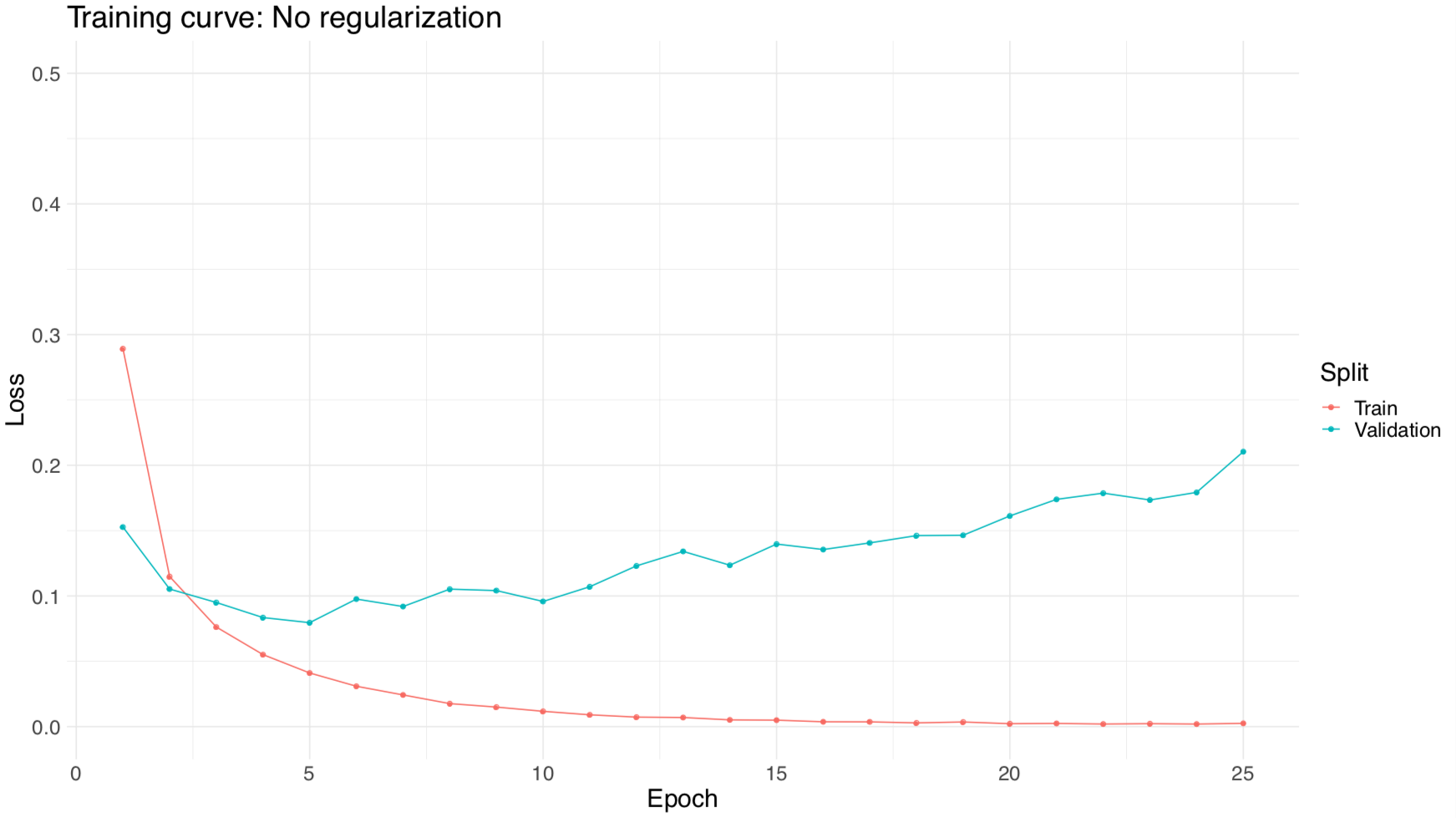
REGULARIZATION
Learning means solving the following optimization problem:
\text{argmin}_{W} \ \ell(y, f(X))
where f(X) = neural net output
REGULARIZATION
One way to regularize is introduce penalties and change
\text{argmin}_{W} \ \ell(y, f(X))
REGULARIZATION
\text{argmin}_{W} \ \ell(y, f(X))
to
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda R(W)
One way to regularize is introduce penalties and change
REGULARIZATION
A familiar why to regularize is introduce penalties and change
\text{argmin}_{W} \ \ell(y, f(X))
to
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda R(W)
where R(W) is often the L1 or L2 norm of W. These are the well known ridge and LASSO penalties, referred to as weight decay by neural net community
L2 REGULARIZATION
We can limit the size of the L2 norm of the weight vector:
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda ||W||_2
where
||W||_2 = \sum^p_{j=1} w_j^2
L1/L2 REGULARIZATION
We can limit the size of the L2 norm of the weight vector:
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda ||W||_2
where
||W||_2 = \sum^p_{j=1} w_j^2
We can do the same for the L1 norm. What do these penalties do?
SHRINKAGE
L1 and L2 penalties shrink the weights towards 0
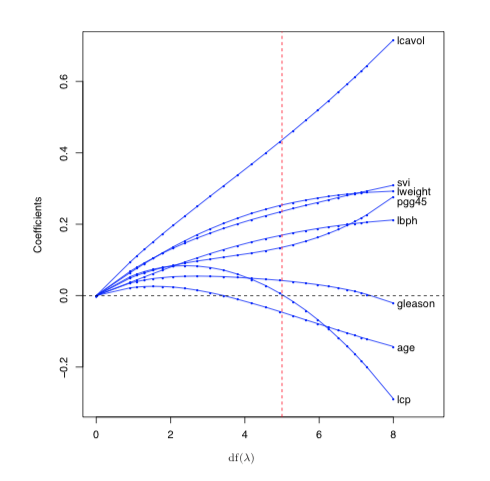
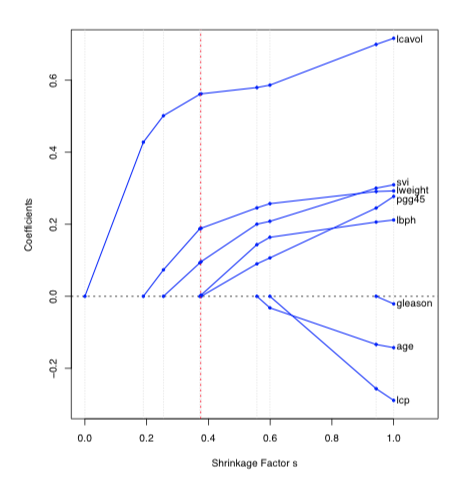
L2 Penalty
L1 Penalty
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. New York: Springer series in statistics, 2001.
SHRINKAGE
L1 and L2 penalties shrink the weights towards 0
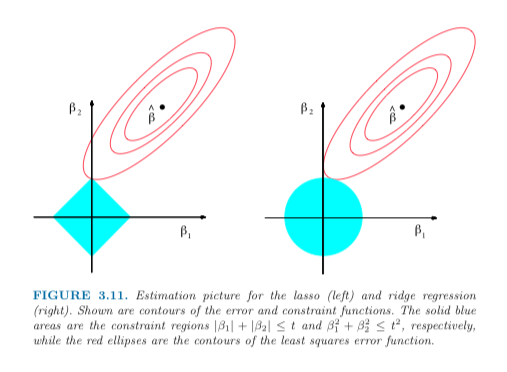
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. New York: Springer series in statistics, 2001.
SHRINKAGE
L1 and L2 penalties shrink the weights towards 0
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. New York: Springer series in statistics, 2001.
Why is this a "good" idea?
STOCHASTIC REGULARIZATION
Often, we will inject noise into the neural network during training. By far the most popular way to do this is dropout
STOCHASTIC REGULARIZATION
Often, we will inject noise into the neural network during training. By far the most popular way to do this is dropout
Given a hidden layer, we are going to set each element of the hidden layer to 0 with probability p each SGD update.
STOCHASTIC REGULARIZATION
One way to think of this is the network is trained by bagged versions of the network. Bagging reduces variance.
STOCHASTIC REGULARIZATION
One way to think of this is the network is trained by bagged versions of the network. Bagging reduces variance.
Others have argued this is an approximate Bayesian model
STOCHASTIC REGULARIZATION
Many have argued that SGD itself provides regularization
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
There is an entire literature on the best way to do this initialization
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
There is an entire literature on the best way to do this initialization
- Normal
- Truncated Normal
- Uniform
- Orthogonal
- Scaled by number of connections
- etc
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
Train model on auxiliary task where lots of data is available
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
Train model on auxiliary task where lots of data is available
Use final weight values from previous task as initial values and "fine tune" on primary task
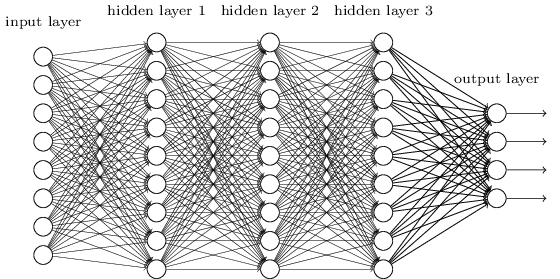
STRUCTURAL REGULARIZATION
However, the key advantage of neural nets is the ability to easily include properties of the data directly into the model through the network's structure
Convolutional neural networks (CNNs) are a prime example of this (Kun will discuss CNNs)
BONUS: BACKPROP FOR MLPs
Perceptron -> MLP
With a small change, we can turn our perceptron model into a multilayer perceptron
- Instead of just one linear combination, we are going to take several, each with a different set of weights (called a hidden unit)
- Each linear combination will be followed by a nonlinear activation
- Each of these nonlinear features will be fed into the logistic regression classifier
- All of the weights are learned end-to-end via SGD
MLPs learn a set of nonlinear features directly from data
"Feature learning" is the hallmark of deep learning approachs
MULTILAYER PERCEPTRONS (MLPs)
Let's set up the following MLP with 1 hidden layer that has 3 hidden units:
X_1
X_2
Pr(y = 1 | X_1, X_2)
Each neuron in the hidden layer is going to do exactly the same thing as before.
h_1
h_2
h_3
o
MULTILAYER PERCEPTRONS (MLPs)
X_1
X_2
h_1
h_2
h_3
o
Computations are:
o = b_o + \sum^3_{j=1} w_{oj}*h_j
p
p = \frac{1}{1 + exp(-o)}
h_j = \phi(w_{1j}*X_1 + w_{2j}*X_2 + b_j)
MULTILAYER PERCEPTRONS (MLPs)
X_1
X_2
h_1
h_2
h_3
o
Computations are:
o = b_o + \sum^3_{j=1} w_{oj}*h_j
p
p = \frac{1}{1 + exp(-o)}
h_j = \phi(w_{1j}*X_1 + w_{2j}*X_2 + b_j)
Output layer weight derivatives
\frac{\partial \ell}{\partial w_{oj}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial w_{oj}}
MULTILAYER PERCEPTRONS (MLPs)
X_1
X_2
h_1
h_2
h_3
o
Computations are:
o = b_o + \sum^3_{j=1} w_{oj}*h_j
p
p = \frac{1}{1 + exp(-o)}
h_j = \phi(w_{1j}*X_1 + w_{2j}*X_2 + b_j)
Output layer weight derivatives
\frac{\partial \ell}{\partial w_{oj}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial w_{oj}}
= (p-y)*p*(1-p)*h_j
MULTILAYER PERCEPTRONS (MLPs)
X_1
X_2
h_1
h_2
h_3
o
Computations are:
o = b_o + \sum^3_{j=1} w_{oj}*h_j
p
p = \frac{1}{1 + exp(-o)}
h_j = \phi(w_{1j}*X_1 + w_{2j}*X_2 + b_j)
\frac{\partial \ell}{\partial w_{1j}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial h}*\frac{\partial h}{\partial w_{1j}}
Hidden layer weight derivatives
\frac{\partial \ell}{\partial w_{oj}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial w_{oj}}
Output layer weight derivatives
= (p-y)*p*(1-p)*h_j
MULTILAYER PERCEPTRONS (MLPs)
X_1
X_2
h_1
h_2
h_3
o
Computations are:
o = b_o + \sum^3_{j=1} w_{oj}*h_j
p
p = \frac{1}{1 + exp(-o)}
h_j = \phi(w_{1j}*X_1 + w_{2j}*X_2 + b_j)
\frac{\partial \ell}{\partial w_{1j}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial h}*\frac{\partial h}{\partial w_{1j}}
Hidden layer weight derivatives
\frac{\partial \ell}{\partial w_{oj}} = \frac{\partial \ell}{\partial p}*\frac{\partial p}{\partial o}*\frac{\partial o}{\partial w_{oj}}
Output layer weight derivatives
= (p-y)*p*(1-p)*h_j
= (p-y)*p*(1-p)*h_j*(1-h_j)*X_1
(if we use a sigmoid activation function)
MLP Terminology
X_1
X_2
Pr(y = 1 | X_1, X_2)
h_1
h_2
h_3
o
X_1
X_2
Pr(y = 1 | X_1, X_2)
h_1
h_2
h_3
o
Forward pass = computing probability from input
MLP Terminology
X_1
X_2
Pr(y = 1 | X_1, X_2)
h_1
h_2
h_3
o
Forward pass = computing probability from input
MLP Terminology
Backward pass = computing derivatives from output
X_1
X_2
Pr(y = 1 | X_1, X_2)
h_1
h_2
h_3
o
Forward pass = computing probability from input
MLP Terminology
Backward pass = computing derivatives from output
Hidden layers are often called "dense" layers
BMI 707 / EPI 290: Week 2 Lab
By beamandrew
