Global Motion Planning without Decomposing Collision-Free Space
Bernhard Paus Græsdal
Amazon Presentation - September 2025



Motivation
1. Avoid decomposing the collision-free space into safe regions
"Efficient Mixed-Integer Planning for UAVs in Cluttered Environments", Deits et al. 2015
2. Planning on the contact manifold
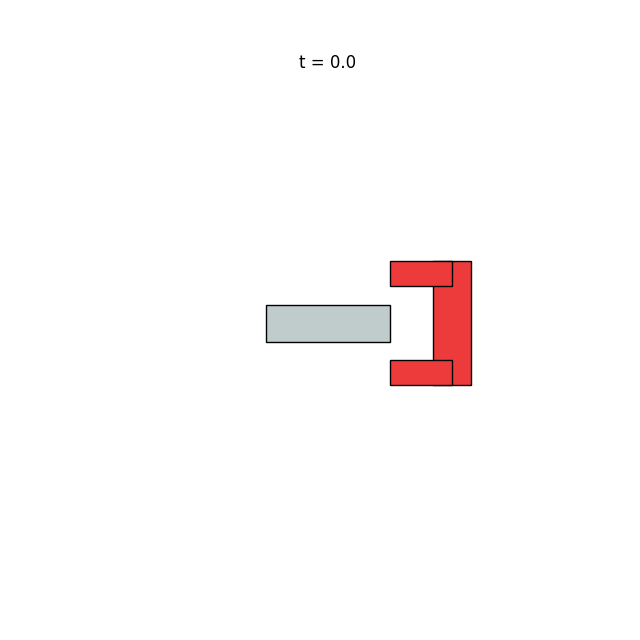
\( \rightarrow \)
Start configuration
End configuration
- A good convex relaxation \( \implies \) We can ~solve the nonconvex problem!
Convex Relaxations
- Success of GCS comes from convex relaxations of nonconvex problems
- We can solve convex programs to global optimality and fast
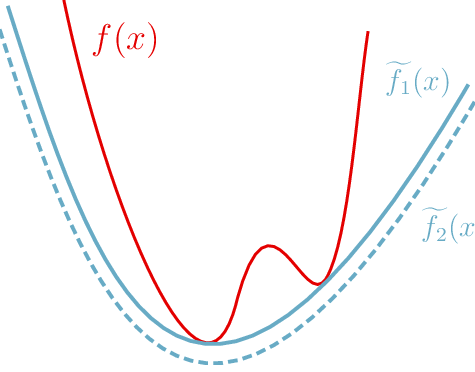
\( f(x) \) is the nonconvex function
Two different convex relaxations:
\( \tilde{f_1}(x) \) gives correct minimum AND minimizer
\( \tilde{f_2}(x) \) gives correct minimizer
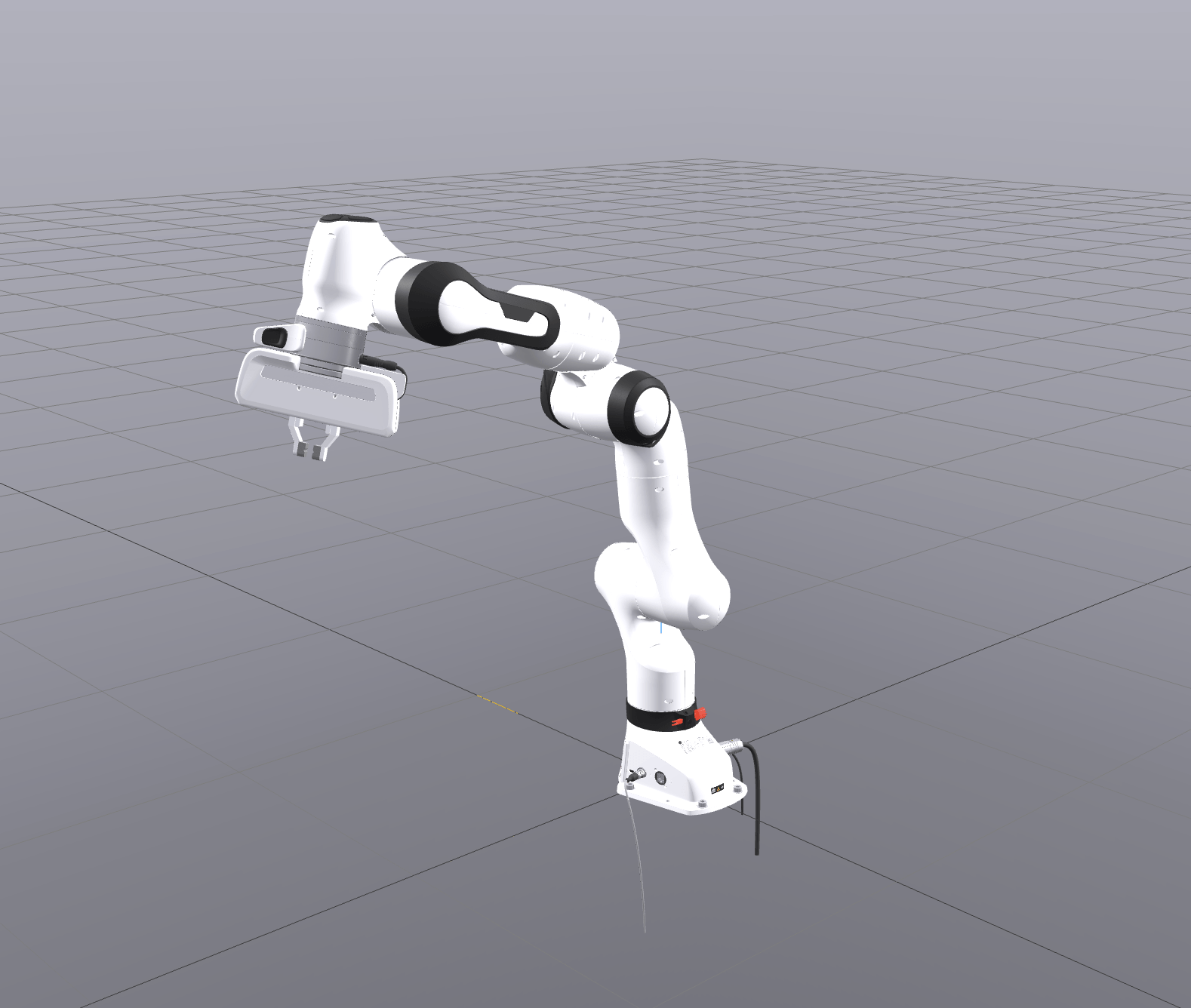
Motion Planning for Robotic Manipulation
\(\leftarrow \) Already common!
(Franka Panda model in Drake)
- Start with motion planning with ellipsoids for collision-geometry and obstacles
(Ellipsoids are special cases of basic semi-algebraic sets: we can generalize to polynomial descriptions later)
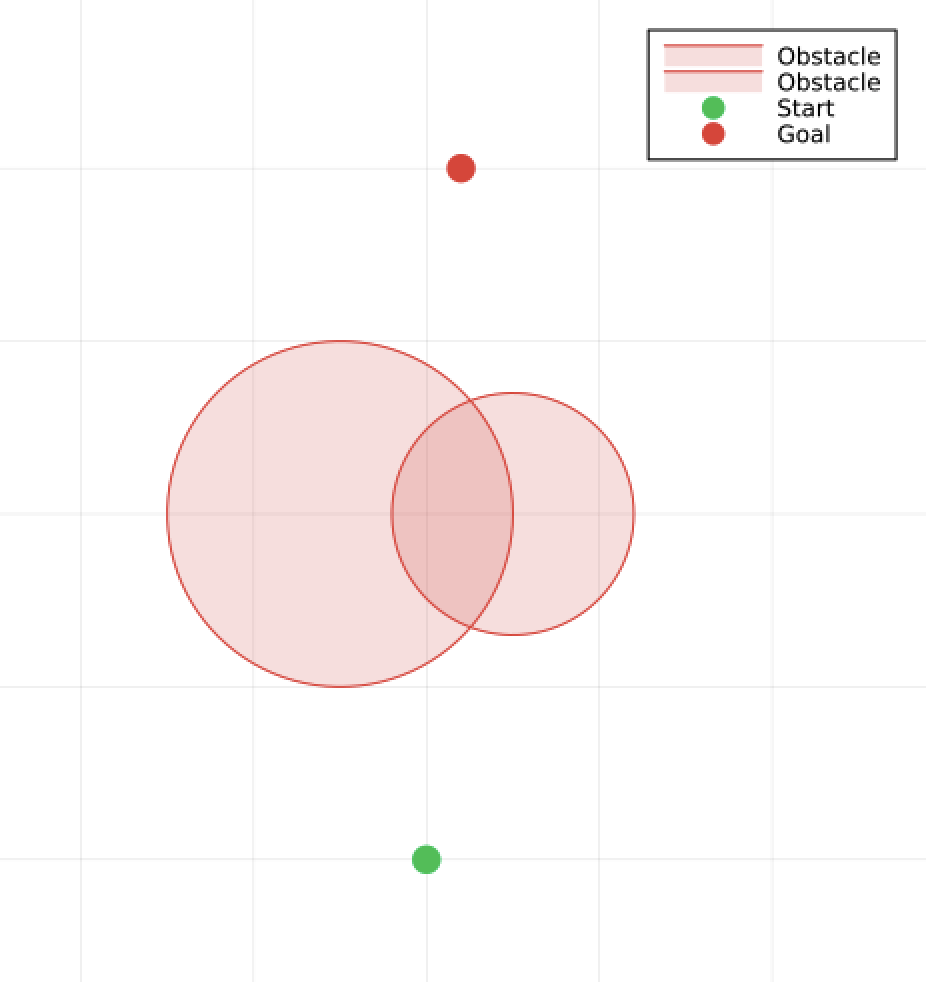
- Start with a simple 2D motion planning problem:
Convex Relaxations for Motion Planning
Trajopt Problem (nonconvex)
Now, we understand theoretically why:
The relaxation provably solves the problem in a lifted space (3D):
- The rank of the solution corresponds to the dimension of the lifted space
- Relaxation is tight when the shortest path lives in the original space
First tried the "standard" semidefinite relaxation, but it is often is often weak:
Although we did not know why
(Not tight)
(Tight)
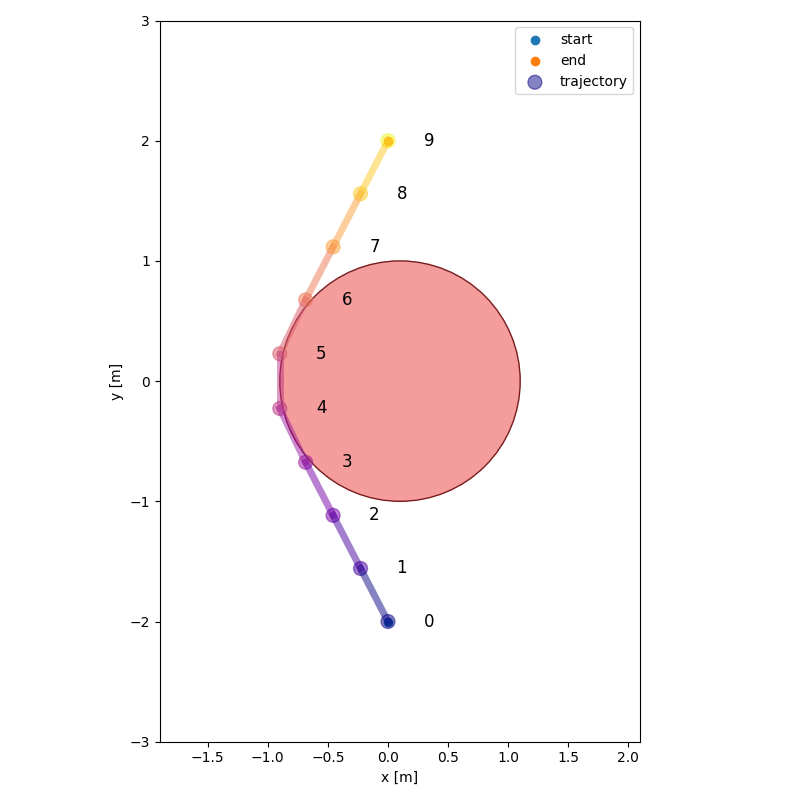
First step: Formulate a nonconvex problem formulation that guarantees a trajectory to be collision free:
Can we do better? (Yes we can)
\(\gamma_0\)
\(\gamma_d\)
\(\gamma_1\)
\( c \)
\( r \)
- Non-convex in control points, but always quadratic
- Relaxation degree is independent of bezier curve degree: fits into second-order relaxation
- The math works out beautifully with polynomial trajectories and the Bernstein basis
where \( \gamma \) are the control points of a Bezier curve
- Collision-free condition becomes a Polynomial Matrix Inequality (PMI) and a PSD constraint:
\(\gamma_0\)
\(\gamma_d\)
\(\gamma_1\)
\( c \)
\( r \)
Second step: Formulate strong convex relaxation of the nonconvex motion planning problem:
- Collision-free planning = nonnegativity of a polynomial \( p(x) \geq 0 \) over a set defined by collision-free condition
(Quadratic module must be Archimedean)
- Theoretically more expressive (potentially more expensive)
(Intuition: All nonnegative polynomials can be written as SOS of rational functions) - For this problem, we obtain very good relaxations at a lower cost
- A common approach is Sums-of-Squares/Lasserre's Hierarchy
However, this is too weak for this problem.
- We use sums-of-squares of rational functions and SOS matrices
We obtain tight relaxations with smooth trajectories that are entirely collision-free:
(in contrast to i.e. piecewise linear discretized trajectories)
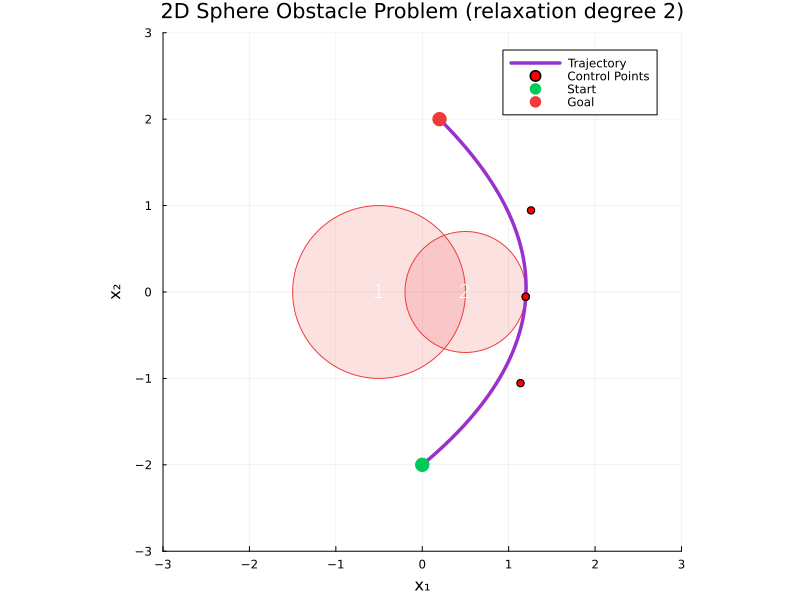
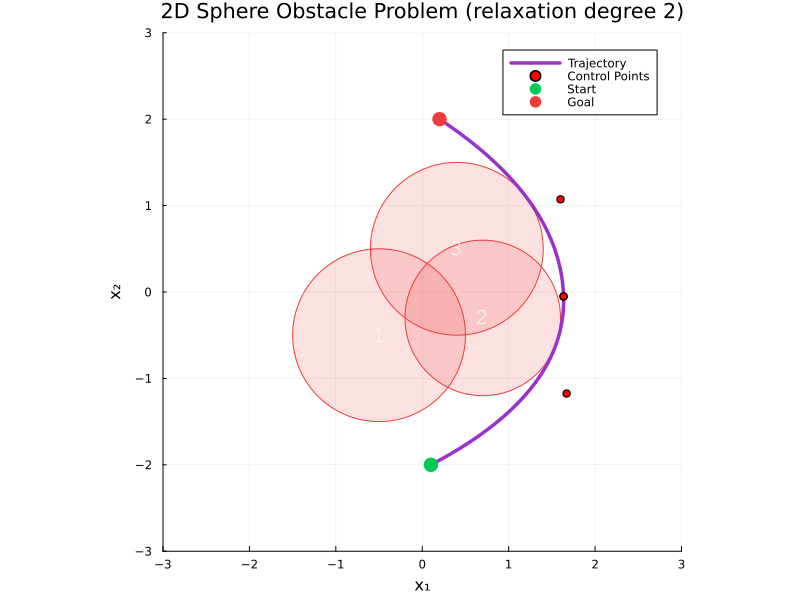
(NB: spheres are only discretized for visualization)
We can extend with robot geometry:
Single robot planning:
Multirobot repositioning:
NB: Preliminary results
Looking ahead
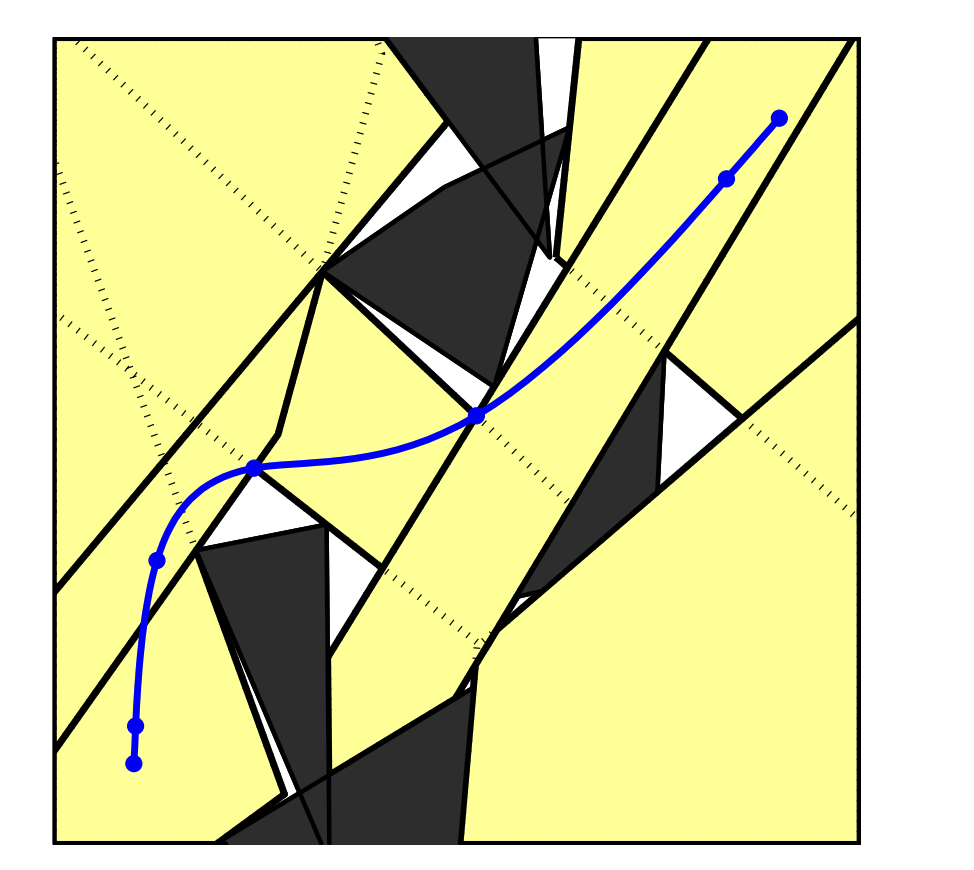
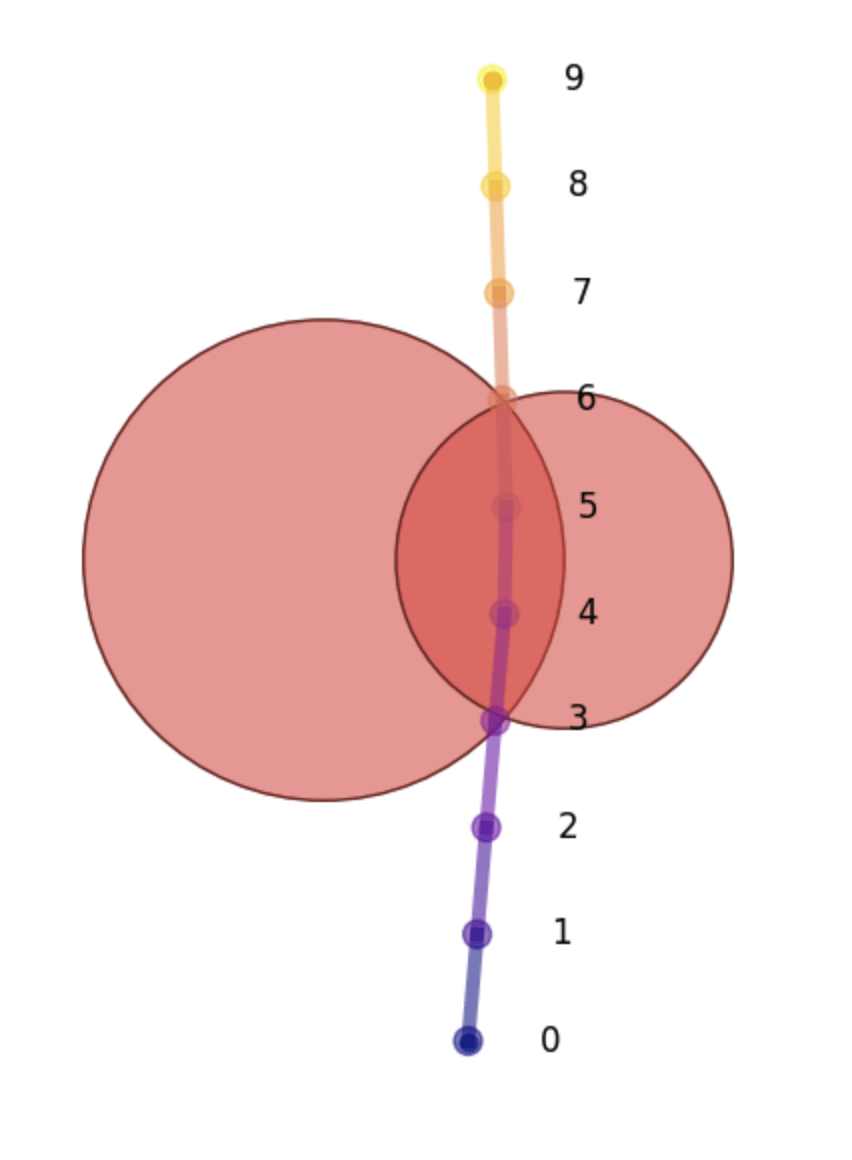
The relaxation allows us to "see around corners":
We now have a visibility oracle:
- Much stronger than straight-line visibility
- Potentially cheap
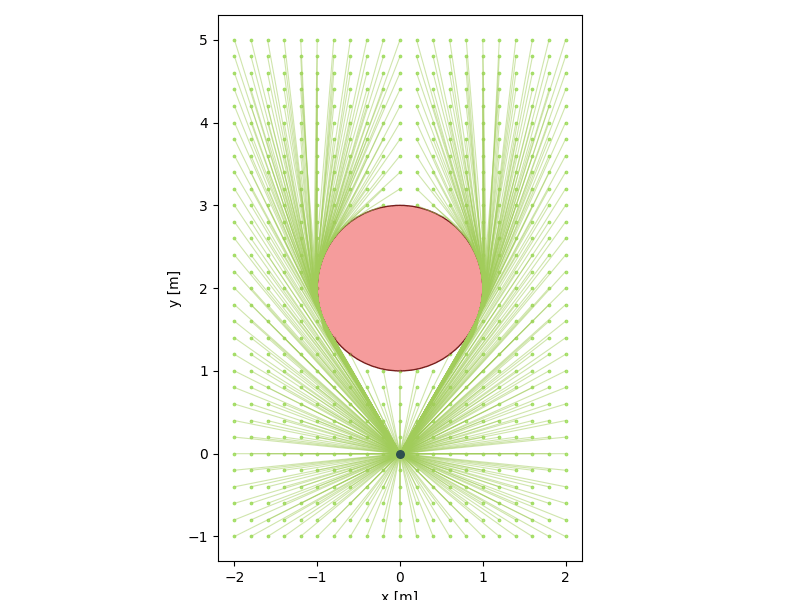
Start
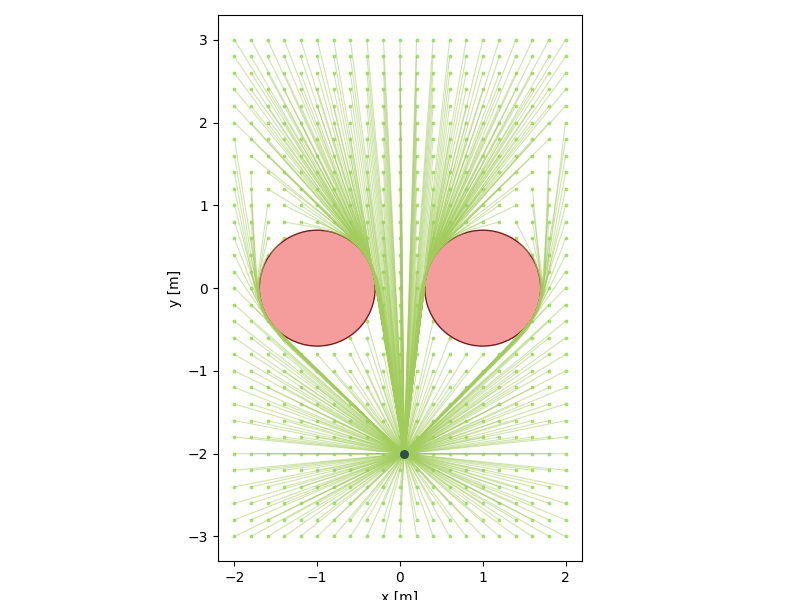
Start
\( \implies \) Could be very powerful. We're still exploring applications.
Let us try RRT*
Example: Plug-and play our oracle into your favorite sampling-based planner
Straight-line visibility (standard)
Visibility oracle (ours)
NB: Preliminary results
We can add in robot geometry:
NB: Preliminary results
(Only ~100 samples, but highlights sliding along contact manifolds)
Thank you!
Global Motion Planning without Decomposing Collision-Free Space
Bernhard Paus Græsdal



Global Motion Planning without Decomposing Collision-Free Space - Amazon Fall 2025
By Bernhard Paus Græsdal


