The effect of tightening constraints for semidefinite relaxations: A case study

Bernhard Paus Græsdal

RLG Short Talk - Fall 2024

Motivation

Some questions that have been asked in this lab:

  • What can you do when the relaxation is loose?
  • How much does tightening constraints help?
  • What tightening constraints should you add?

Goal for this talk

Provide a simple case study with some empirical answers to these questions

Case-study: Translational Pushing of a Box

Problem formulation

Decision variables:

  • \( q^a_t \) finger x-position
  • \( q^u_t \) box x-position
  • \( u_t \) commanded finger x-position
  • \( n_t \) applied normal impulse

Quasi-Dynamic EoMs:

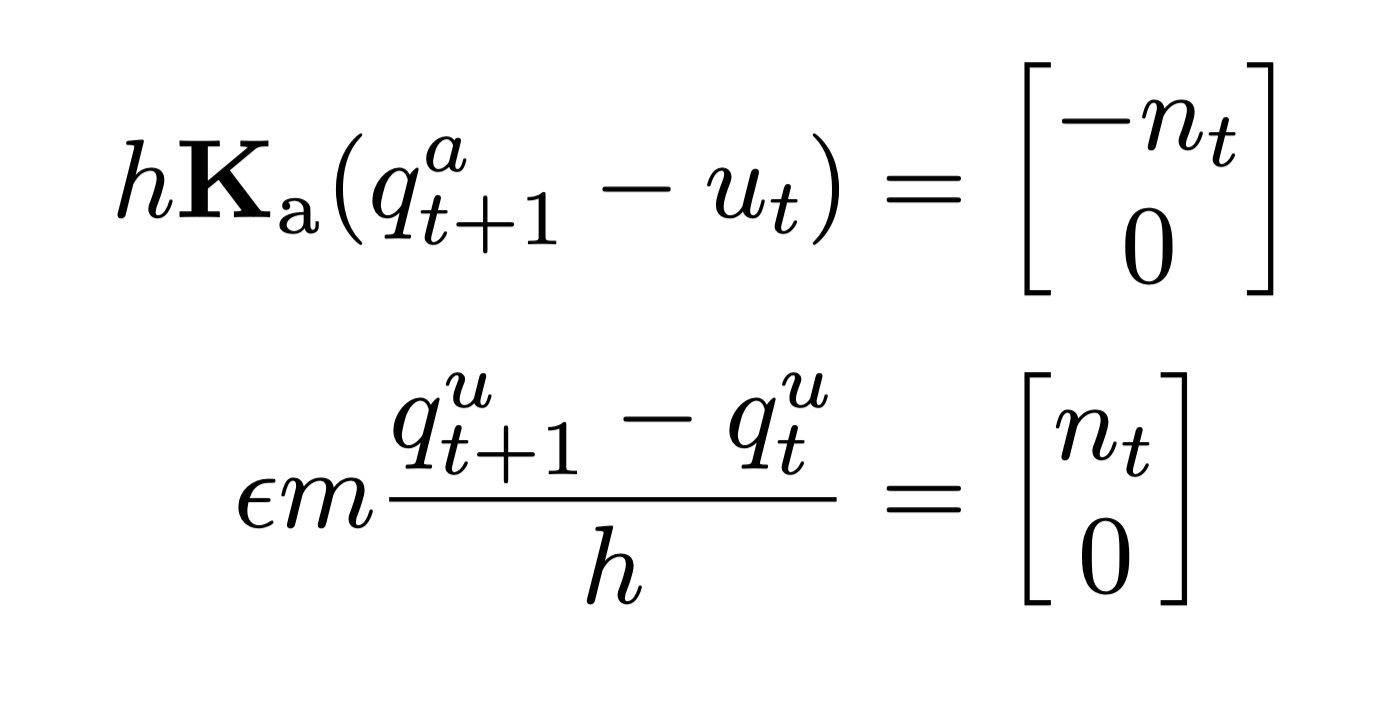
Nonconvex trajectory optimization problem

Nonconvex complementarity constraints!

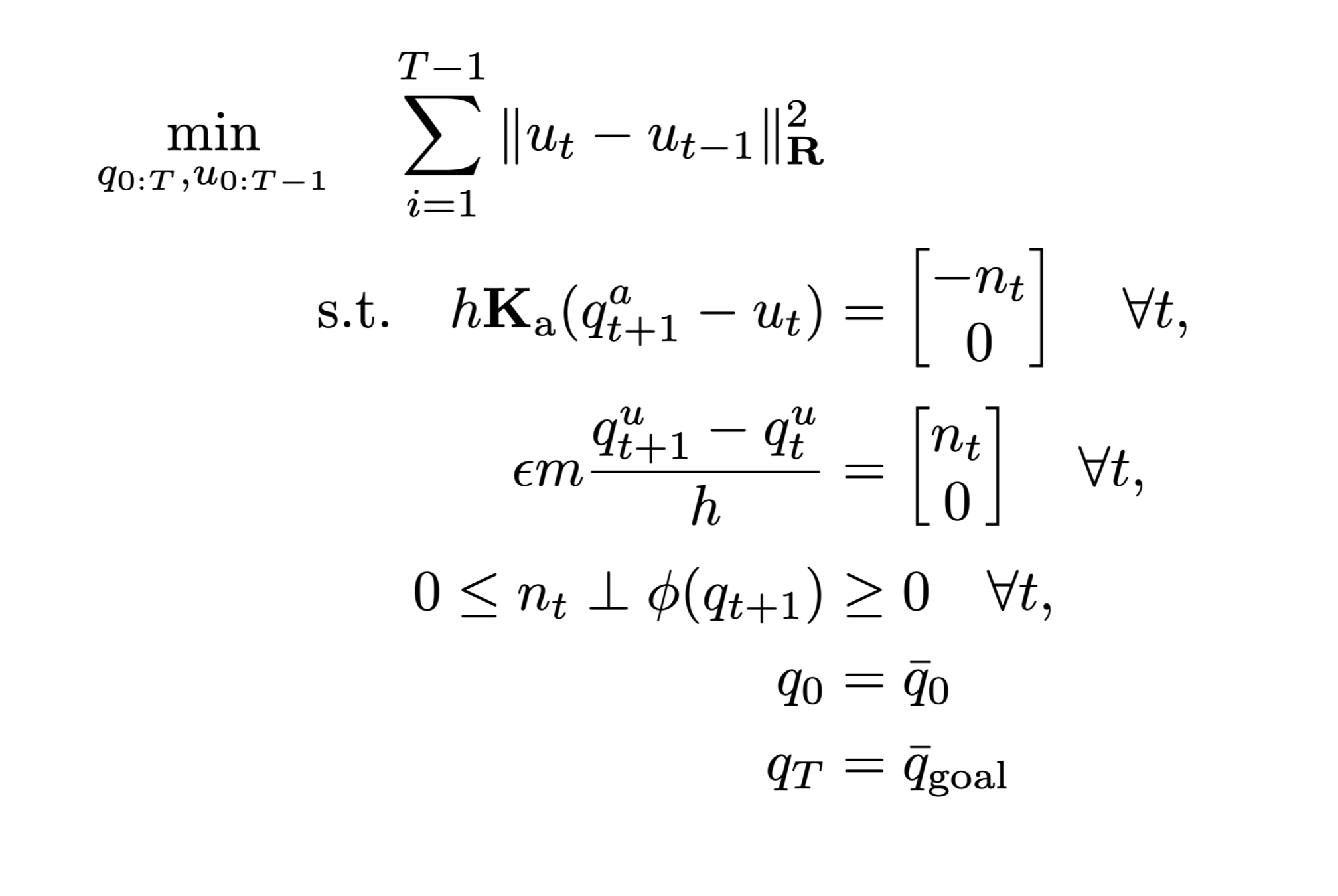
Optimal solution

Optimal cost:

\( C_\text{opt} = 0.968 \)

For horizon \( T = 10 \)

How to solve the nonconvex trajopt?

Our problem is a QCQP:

Let's get a lower bound by solving a semidefinite relaxation

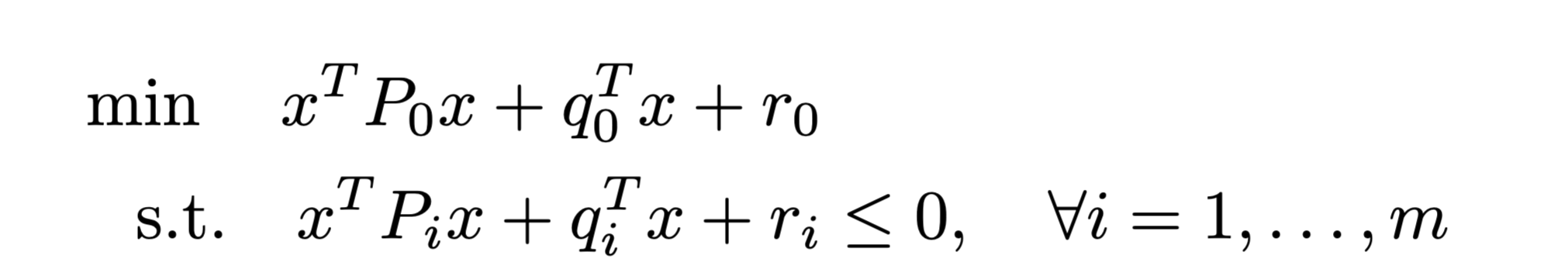
Attempt 1: Exploit no structure

QCQP

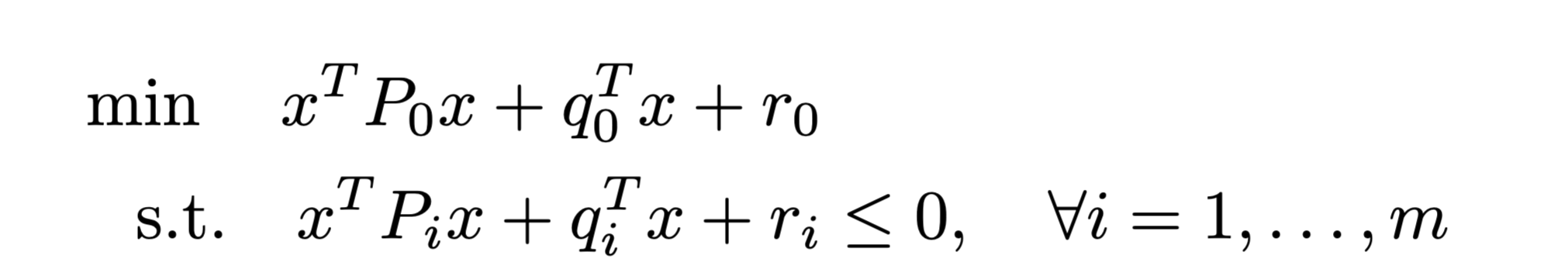
SDR

Exact when \( X = xx^T \iff rank(X) = 1\)

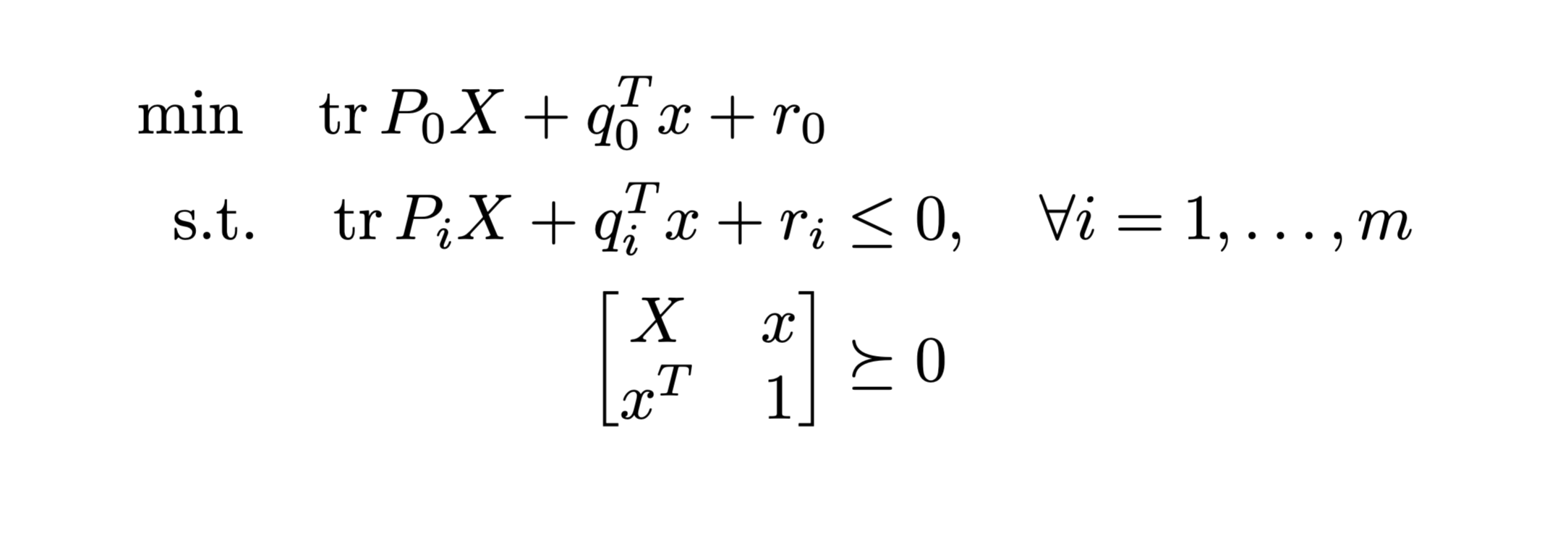
Attempt 1: Result

\( \text{rank}(X) \gg 1 \)

\( C_\text{relaxed} = 0.1 \)

\( C_\text{opt} = 0.968 \)

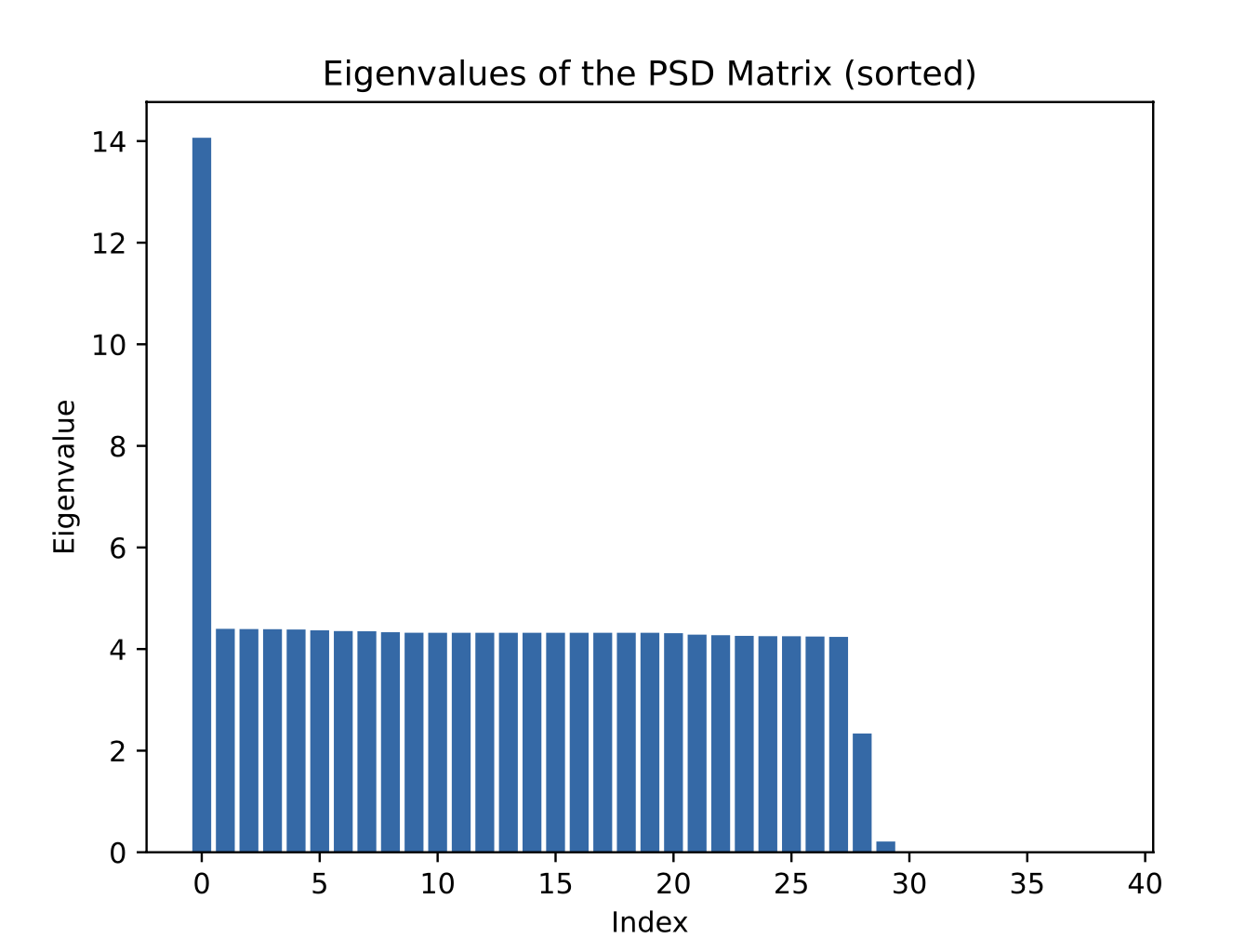
Opt gap = \( -89.67 \% \)

Attempt 2: Eliminate equality constraints

(Equivalent to eliminating equality constraints by parametrizing affine feasible set \( \set{x | Bx = d} = \set{Fz + \hat{x} } \) )

QCQP

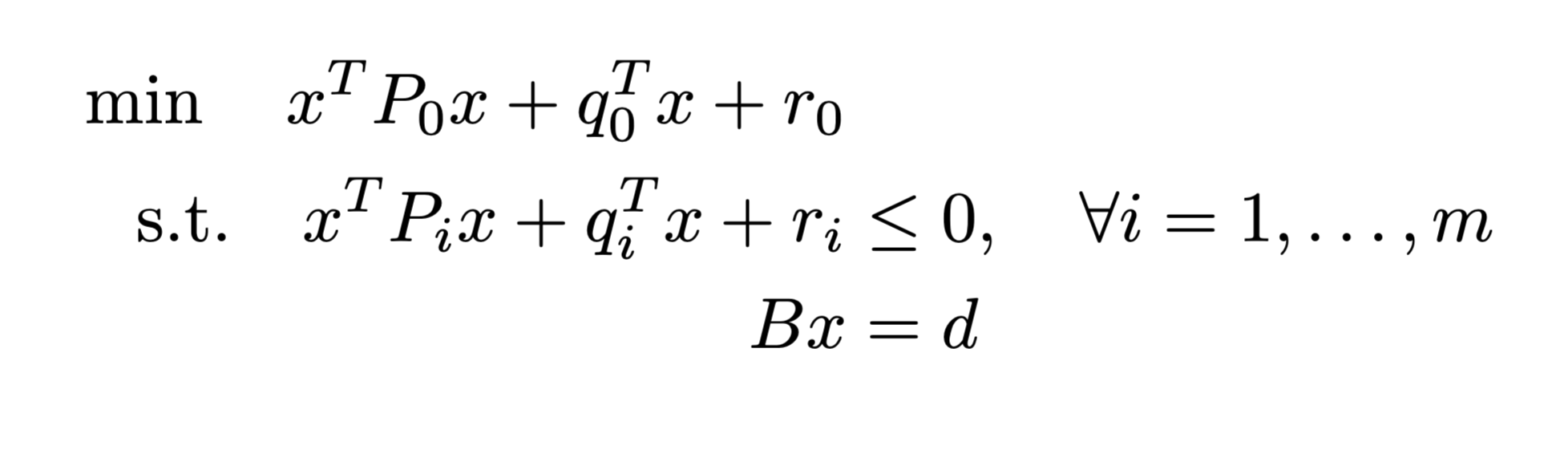
SDR-EQ

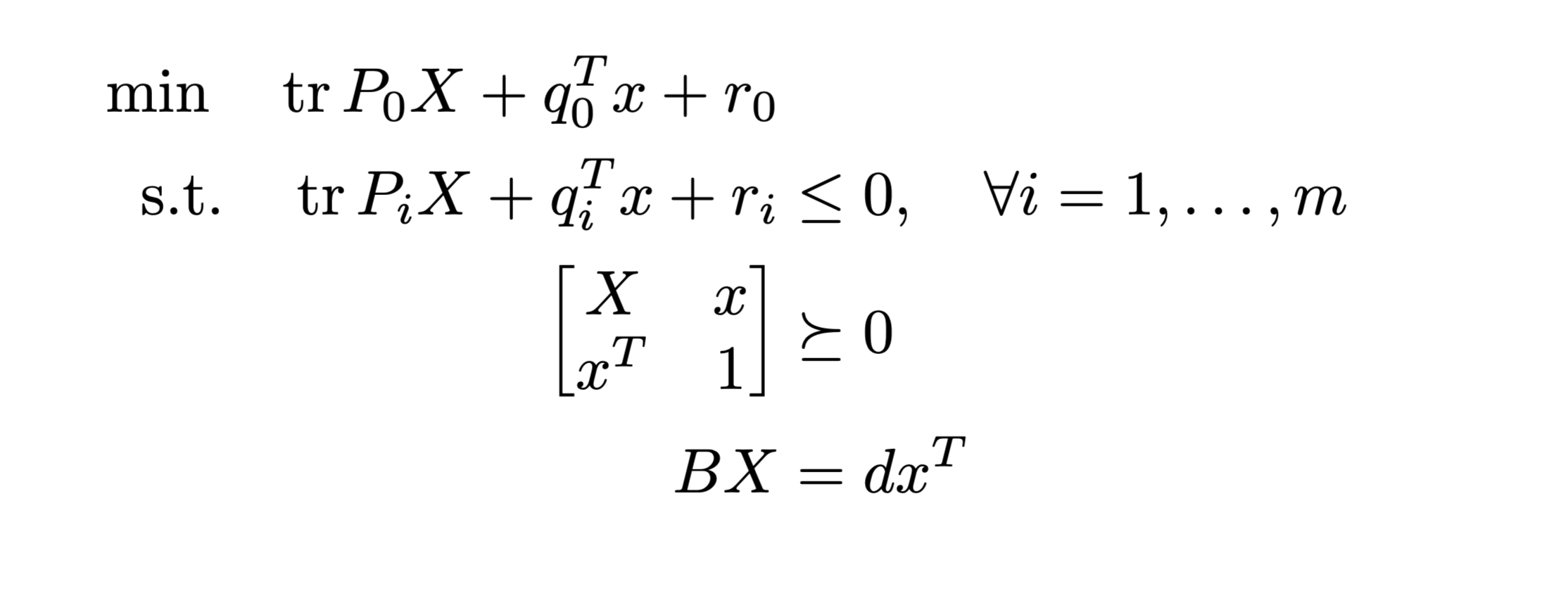
Multiply \( Bx= d\) with \(x^T\) and linearize with \( X = xx^T \)

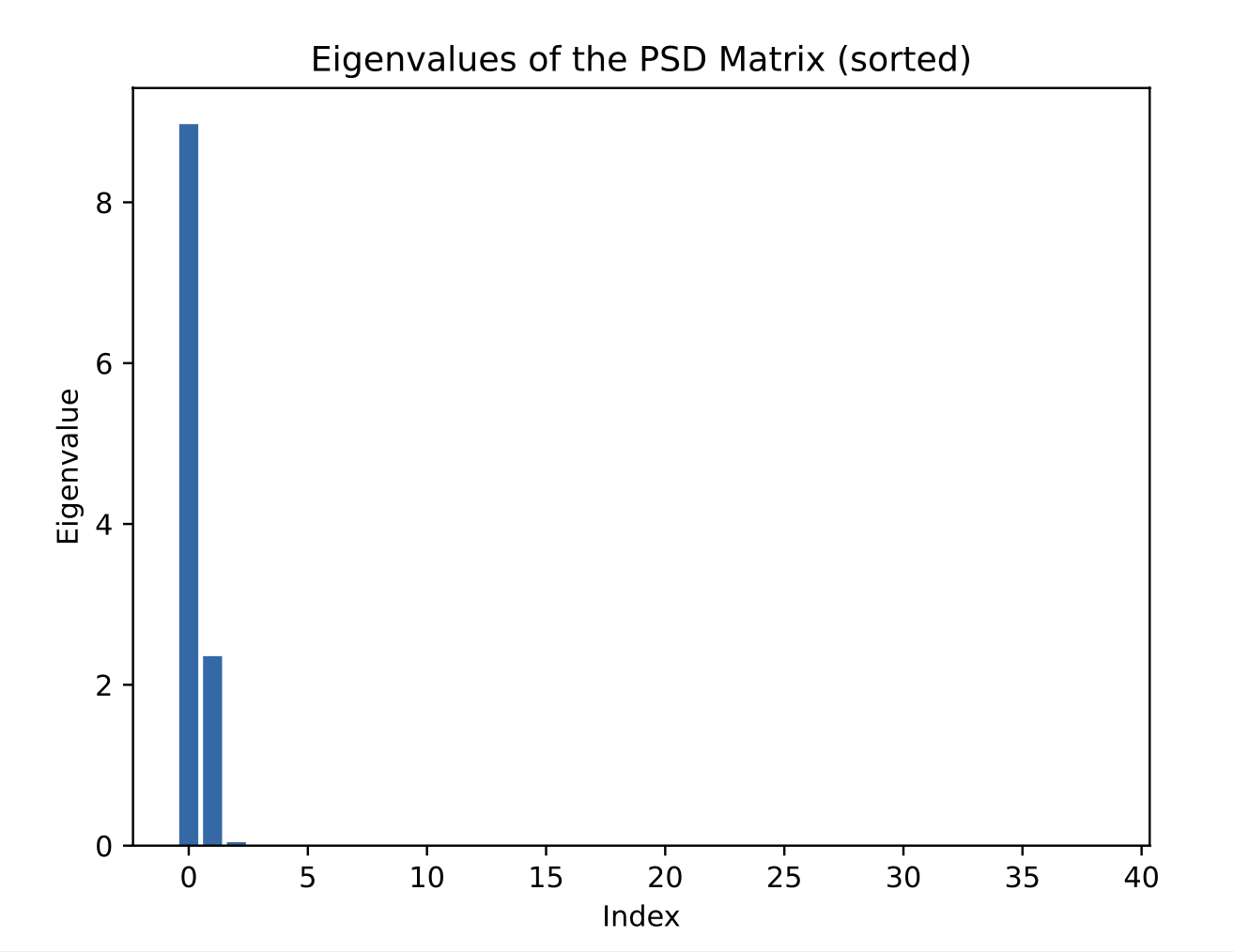
Attempt 2: Result

\( \text{rank}(X) \approx 3 \)

\( C_\text{relaxed} = 0.795 \)

\( C_\text{opt} = 0.968 \)

Opt gap = \(-17.9 \% \)

Note:

You should always eliminate equality constraints.

(either by adding implied constraints or by reparametrization)

Attempt 3: Add implied linear constraints

QCQP

SDR-RLT

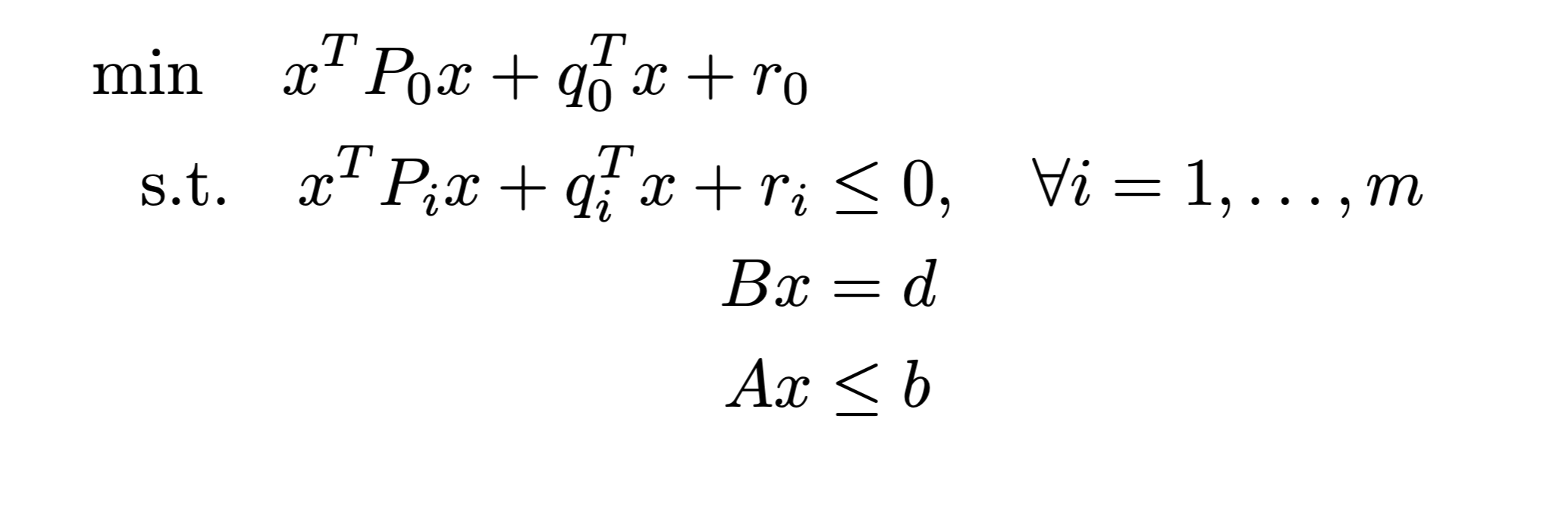
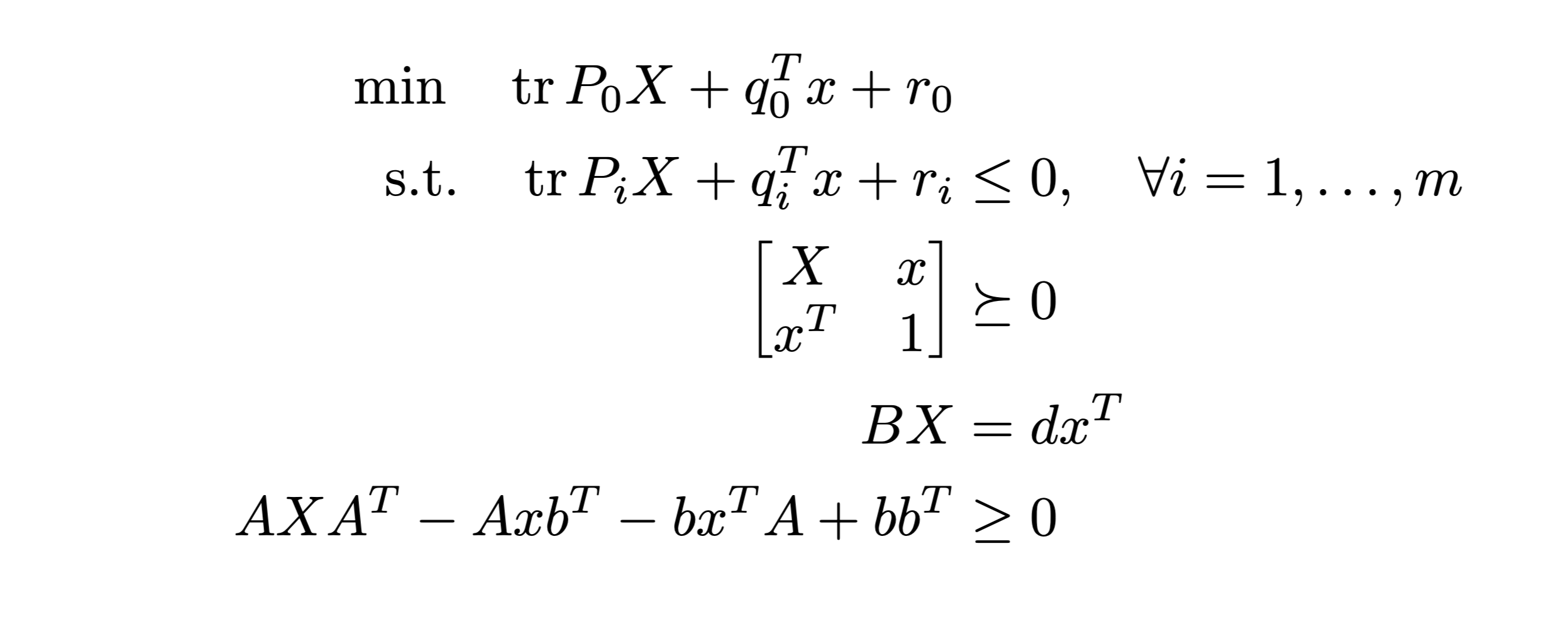
Multiply \( Ax-b \leq 0 \) with its transpose and linearize with \( X = xx^T \)

Attempt 3: Result

\( \text{rank}(X) = 1 \)

\( C_\text{relaxed} = 0.968 \)

\( C_\text{opt} = 0.968 \)

Opt gap = \(0 \% \)

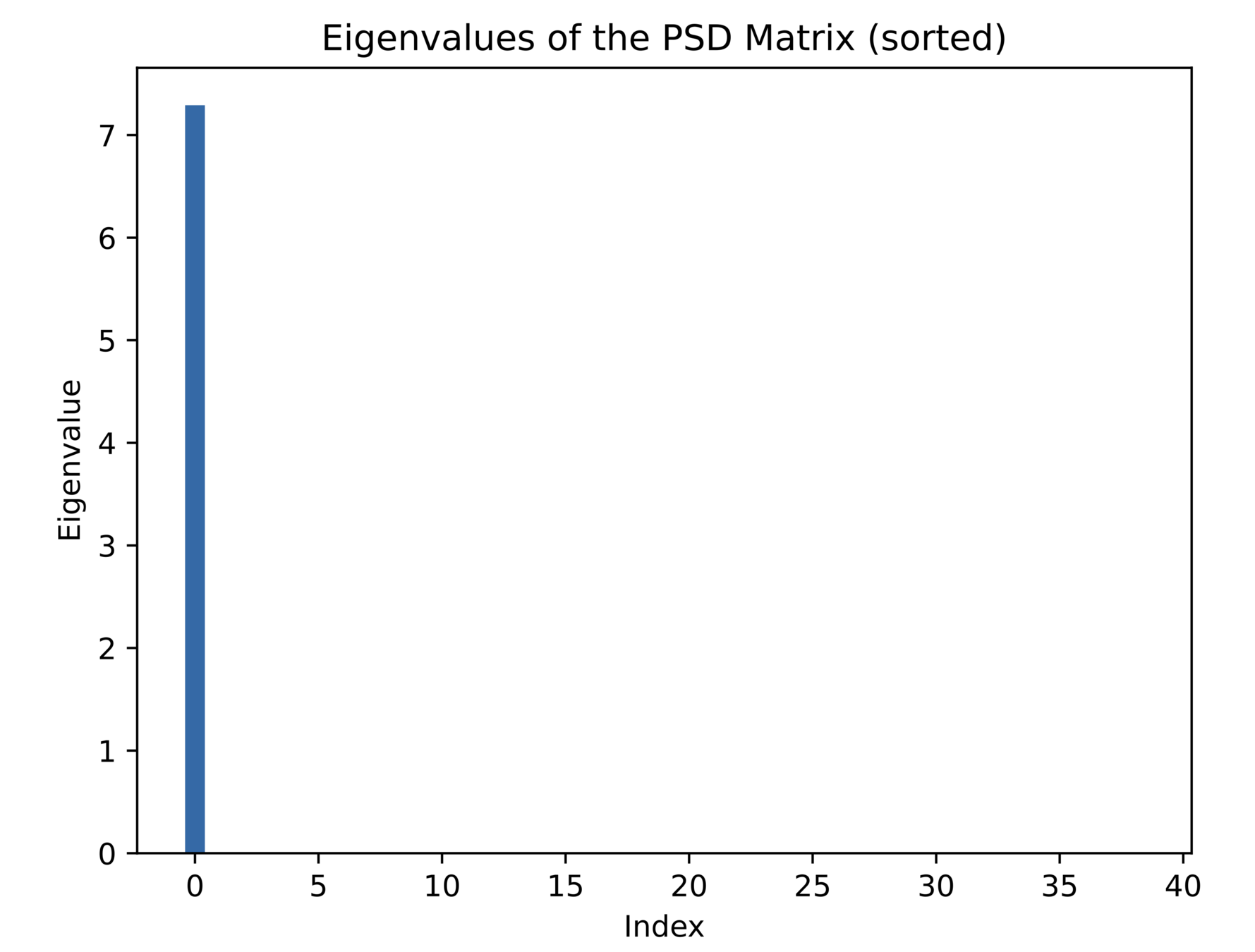
Relaxation is tight!

Inefficient?

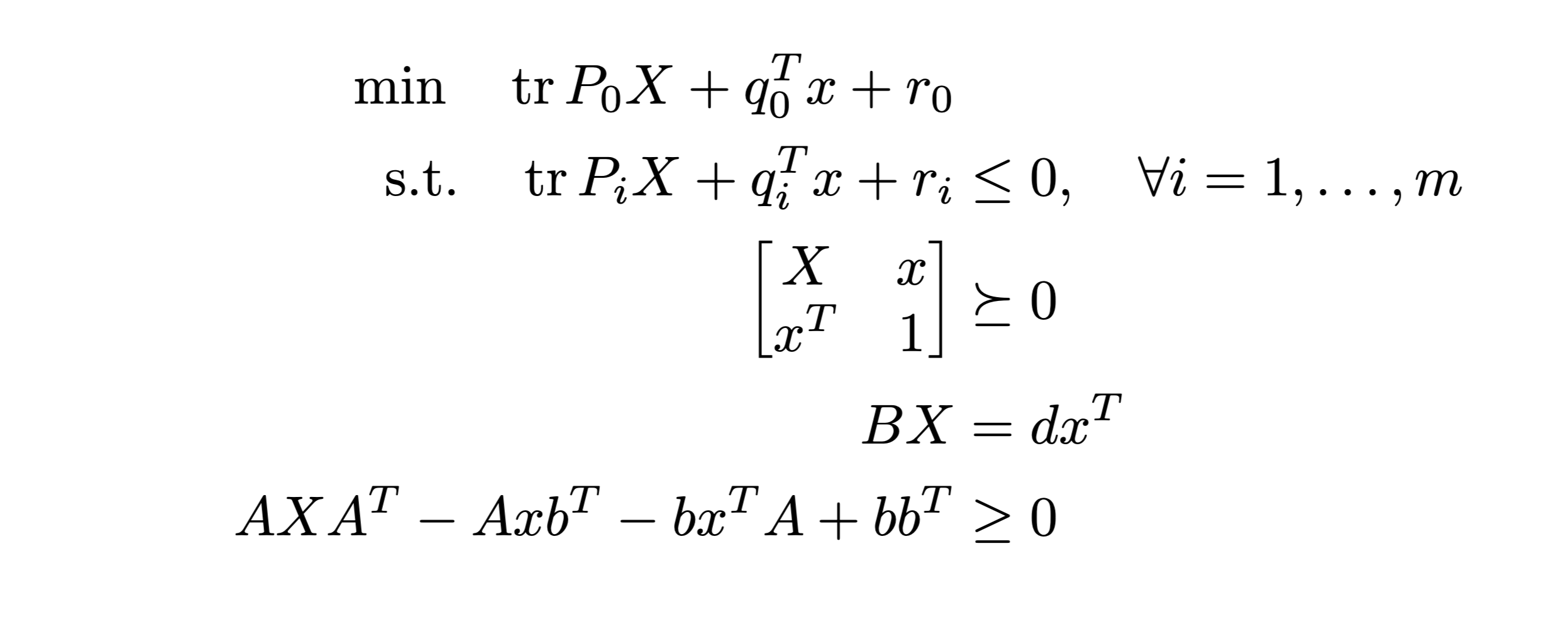
  • Are we generating too many constraints?
  • In our example, most of these are not needed

Let us remove some constraints

  • The implied constraints needed for tightness turn out to be:
n_t \geq 0 \quad \forall t =0, \ldots, T-1
\implies n_k n_l \geq 0 \quad \forall \, k, l = 0, \ldots, T-1, \, k \neq l
  • Take product between all timesteps
  • If we add these implied constraints, solution is tight

Can we leverage band structure?

  • Let's try this here. Only take product between \(n\) successive timesteps:
n_t \geq 0 \quad \forall t =0, \ldots, T-1
\implies n_t n_{t+k} \geq 0 \quad \forall \, t = 0, \ldots, T-1, \, k = 1, \ldots n

 

  • Turns out it is tight for \( n= 5\)  (with \( T = 10 \))
  • I.e. we can not leverage band sparsity and preserve tightness
  • In this toy problem we get rid of \( 82 \% \) of all linear implied constraints (\( 459 \rightarrow 83 \))
  • Previously we have leveraged TO band structure for efficiency

\( n = 1\)

Opt gap = \( -17.6 \% \)

Opt gap = \( -5.5 \% \)

Opt gap = \( -0.06 \% \)

\( n = 3\)

\( n = 4\)

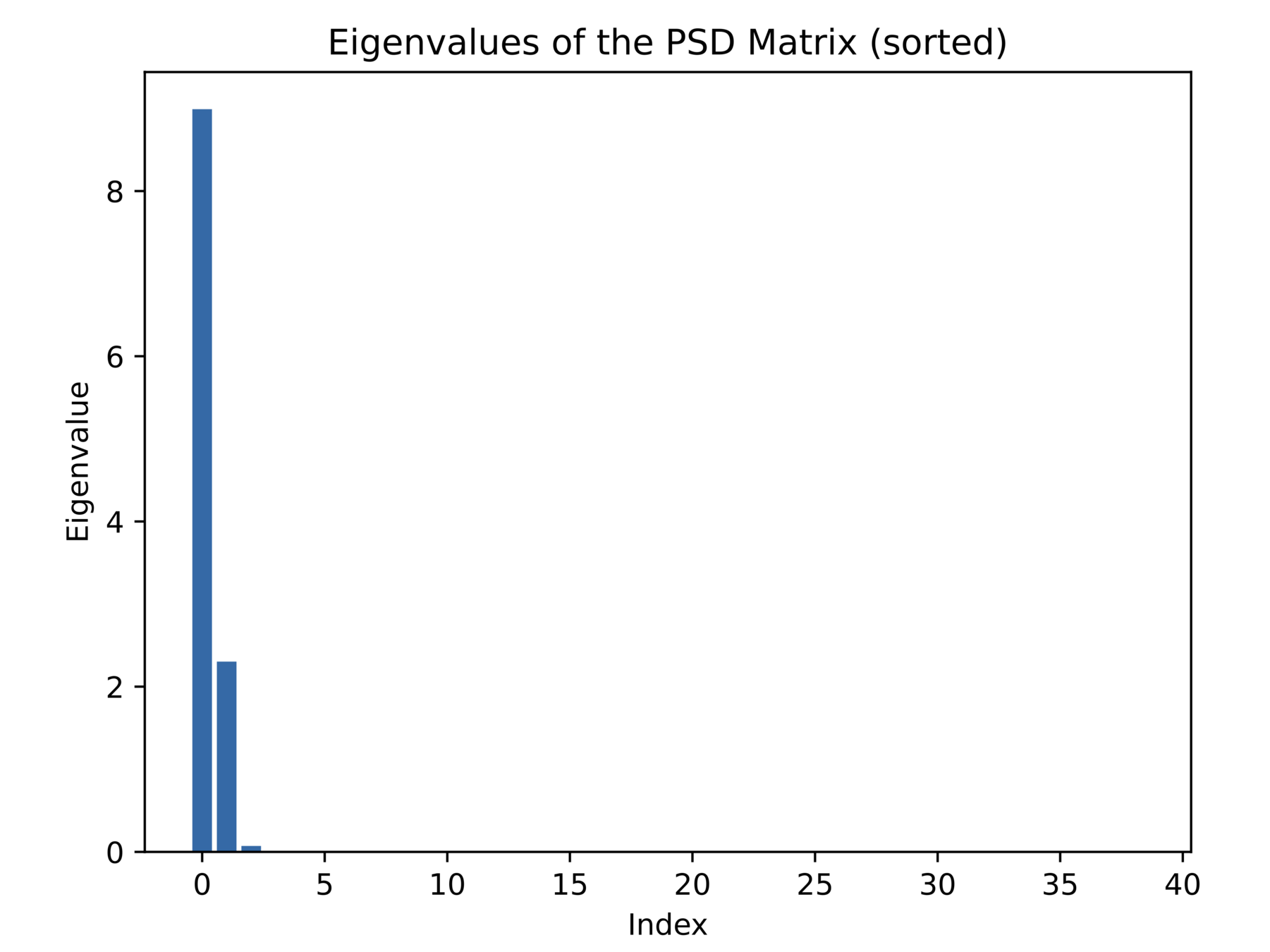
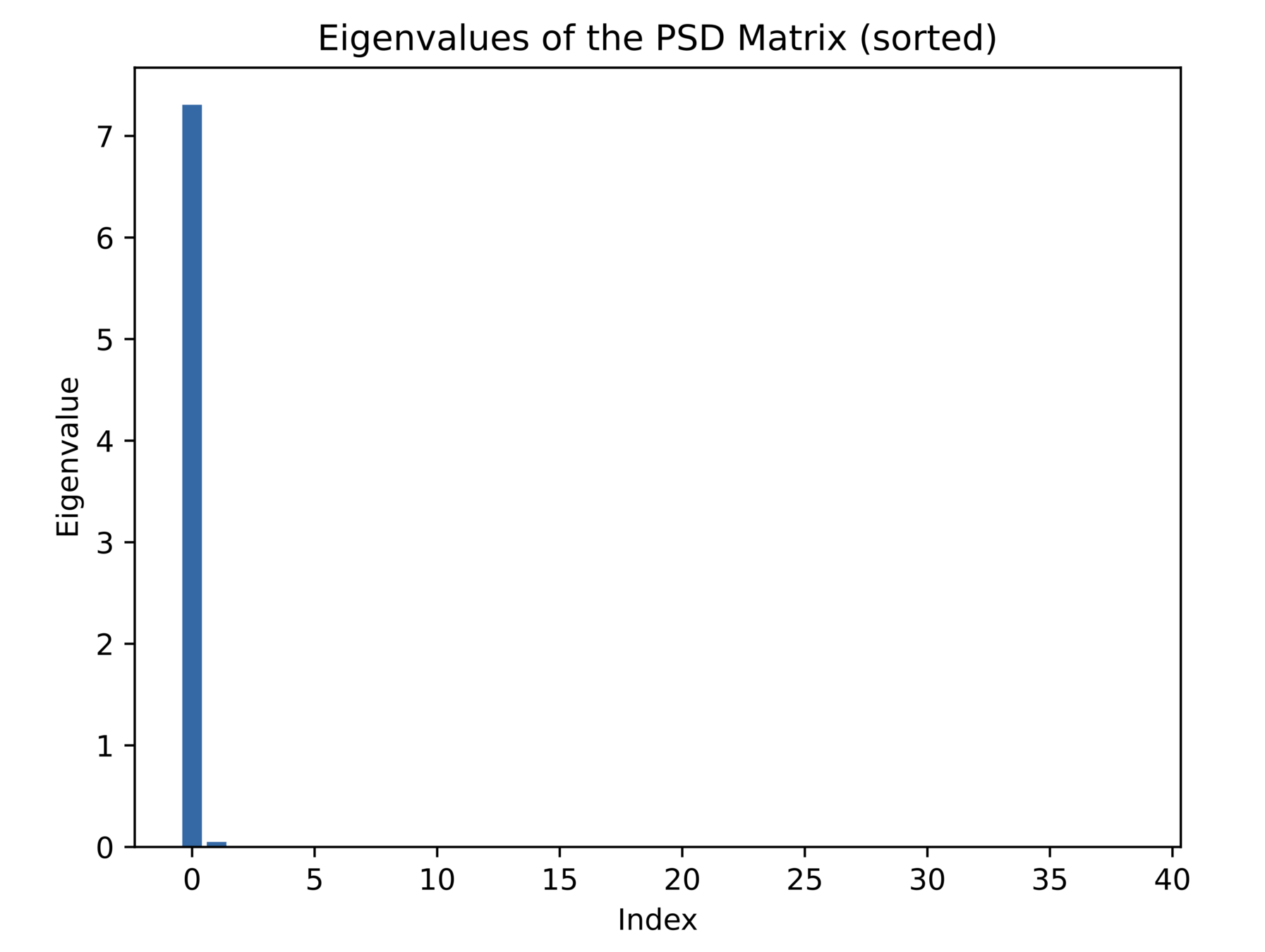
But what if the relaxation is still not tight...?

Okay, so you can:

  • Eliminate linear equality constraints
  • Add all implied linear inequality constraints

What about other constraints?

Generally want to model signed distance as a SOC:

\( \phi \geq \| q^a - c \| \)

constant position of contact point on box

This gives a terrible relaxation (even with all our tricks so far)

\( \phi \)

Opt gap = \( -89.67 \% \)

What constraint is missing?

\( \phi \geq \| q^a - c \| \) and \( n \geq 0 \)

We need to multiply and linearize the SOC too:

\( \phi n \geq \| q_a n - c n \| \)

\( \implies \)

\( \implies \)

Linearize with \( X = xx^T \)

\( X_{\phi n} \geq \| X_{q_a n} - c n \| \)

We multiply a SOCC in \( x \) with a linear constraint in \( x \) to obtain a new SOC in \( (x, X) \).

Now the solution is tight!

A more useful example: With this we can model signed distances exactly in \( \R^2 \) and \( \R^3 \) (we could not do this before!)

(We now allow x and y motion)

This is a general recipe

  • In general: multiply SOCCs and linear constraints in \( x \) to obtain new SOCCs in \( (x,X) \) (which imposes additional structure on the lifted variables).
     
  • One can keep doing this for SOCCs with SOCCs to obtain new SOCCs, and similarly with any convex quadratic constraints.
     
  • See for instance:

[1] R. Jiang and D. Li, “Second order cone constrained convex relaxations for nonconvex quadratically constrained quadratic programming,” J Glob Optim 2019

What if we have convex quadratics?

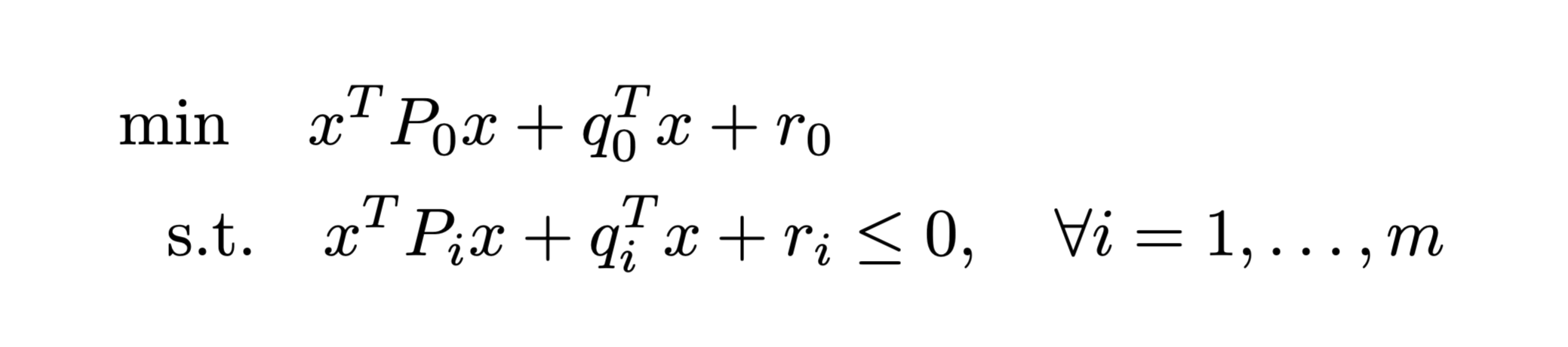
Say \( P_i  \succeq 0 \) for some \(i\).

QCQP

Should we keep the convex constraint?

I.e. add both

and

?

The answer is no.

\text{tr}{(P_i X)} + q_i^T x + r_i \leq 0
x^T P_i x + q_i^T x + r_i \leq 0
S_1 = \set{x | x^T P_i x + q_i^T x + r_i \leq 0}
S_2 = \set{x | \text{tr}{(P_i X)} + q_i^T x + r_i \leq 0 \quad \text{for some} \quad X \succeq xx^T}

Then \( S_2 \subseteq S_1 \).

(i.e. we should only add the linearized quadratic constraint).

Lemma:

Proof:

Suppose \(x \in S_2 \) and \(X \succeq xx^T\).

Then \(0 \geq \text{tr}(P_i X) + Q_i^T x + r_i \geq x^T P_i x + q_i^T x + r_i\), i.e. \( x \in S_1 \).

(Because \(P_i \succeq 0\) and \(X \succeq xx^T \) \(\implies\) \(\text{tr}(P_i X) \geq \text{tr}(P xx^T) \)) \(\square\)

Let

Some conclusions

  • Always eliminate equality constraints
  • Adding linear implied constraints can make a big difference
    • (Does not seem to help for Rebecca's problems?)
  • Leveraging TO band sparsity to reduce the number of implied constraints can reduce tightness
    • (I had not observed this before, but in this toy problem it is very clear)
  • Implied constraints between SOCCs and linear constraints can be very important

A final thought: Working with semidefinite relaxations can feel a bit like this...

Thank you!

RLG Short Talk - Fall 2024

By Bernhard Paus Græsdal

RLG Short Talk - Fall 2024

  • 161

More from Bernhard Paus Græsdal