Intro to Machine Learning

Agenda

• What is Machine Learning
• Machine Learning types of problems
• Intro to some basic ML algorithms
• Case study: apply ML techniques

What is ML

is the study of computer algorithms that improve automatically through experience and by the use of data

(source: https://en.wikipedia.org/wiki/Machine_learning)

Types of ML

Supervised learning

       It is defined by its use of labeled datasets to train algorithms that to classify data or predict outcomes accurately

• Classification uses an algorithm to accurately assign test data into specific categories.
• Regression is used to understand the relationship between dependent and independent variables.

Unsupervised learning

Unsupervised learning is very much the opposite of supervised learning. It features no labels. Instead, our algorithm would be fed a lot of data and given the tools to understand the properties of the data

Clustering - Clustering is a data mining technique which groups unlabeled data based on their similarities or differences.

Dimensionality reduction - While more data generally yields more accurate results, it can also impact the performance of machine learning algorithms (e.g. overfitting) and it can also make it difficult to visualize datasets

Types of ML

Regression

    Regression is used to understand the relationship between     dependent and independent variables.

    Examples: predict the outputs, forecasting the data, analyzing the time series, and finding the causal effect dependencies between the variables

Price house

Problem statement:  We have a dataset with the price of some sold houses. For each house we also have some characteristics: number of rooms, size (m^2).

What can we do with this data?

Build a linear regression model to predict the price.

Price house

Problem statement:  We have a dataset with the price of some sold houses. For each house we also have some characteristics: number of rooms, size (m^2).

What can we do with this data?

Build a linear regression model to predict the price.

If the price is a linear function of the number of rooms and size then we can build a model to predict price house. The model is simply a linear function:

Price(house) = a * number of rooms + b * size

Linear regression

Linear regression is a linear approach to modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables).

In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data.

Price house

What if the response variable is not a linear combination of the predictor variables (features) ?

Let's assume that the price is quadratic increasing with the number of rooms.

Price(house) = a * (number of rooms) ^ 2 + b * size

Can we still use linear regression?

Price house

What if the response variable is not a linear combination of the predictor variables (features) ?

Let's assume that the price is quadratic increasing with the number of rooms.

Price(house) = a * (number of rooms) ^ 2 + b * size

Can we still use linear regression?

Yes, instead of using the features (predictors): number of rooms and size we can use new features (predictors): (number of rooms) ^ 2 and size for the linear regression algorithm.

Working with ML 

Hint 1: Feature engineering is an important part of ML

Working with ML 

Hint 1: Feature engineering is an important part of ML

Success of a ML algorithm very often depends on what features you choose.

We can gather useful information to build the features from a "domain expert".

Features != raw data

Linear regression alg

Linear regression can be implemented using the Least-squares estimation algorithm.

Linear regression alg

Imagine you have some points, and want to have a line that best fits them like this:

Linear regression alg

Text

We have 2 vectors: one is static and the other one is variable. We have to find the best variable vector that minimize the distance between the 2 vectors.

Linear regression alg

Text

We have 2 vectors: one is static and the other one is variable. We have to find the best variable vector that minimize the distance between the vector.

The best fit in the least-squares sense minimizes the sum of squared residuals (a residual being: the difference between an observed value, and the fitted value provided by a model).

https://en.wikipedia.org/wiki/Least_squares

Linear regression alg

https://www.mathsisfun.com/data/least-squares-calculator.html

https://setosa.io/ev/ordinary-least-squares-regression/

Text

https://en.wikipedia.org/wiki/Euclidean_distance

https://www.mathsisfun.com/data/least-squares-regression.html

Linear regression alg

Text

Short Demo: https://www.codingame.com/playgrounds/3771/machine-learning-with-java---part-1-linear-regression

Working with ML

Text

Hint 2: In ML we usually try to minimize a loss function.

https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/LinearRegression.java.html

Clustering

Text

Clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters)

The notion of a "cluster" cannot be precisely defined, which is one of the reasons why there are so many clustering algorithms

Clustering

Text

Homework :)

https://en.wikipedia.org/wiki/Cluster_analysis

https://en.wikipedia.org/wiki/K-means_clustering

https://en.wikipedia.org/wiki/DBSCAN

Other terminology in ML

Text

f(x) = a+b*x1 + c*x2

Features:  x1, x2; need to be linear independent between each other; y needs to be linear dependent on them

Weights: a, b, c

Overfitting: learning too well a specific data set and failing to generalize

Train set = data set on which we train the model

Cross validation set = data set on which we test different algs/params

Test set = the final data set on which we evaluate the choosen alg

Working in ML

Text

Hint 3: ML is not about using a specific algorithm. It is more about modeling the problem as a the right type of ML problem e.g. for the exact same problem we can use different ML techniques and for each ML technique we can use different algorithms.

Anomaly detection

Text

Anomaly detection (aka outlier analysis) is a use case of ML.

Is the problem of finding the data points that deviate from a dataset's normal behavior.

It can be modelled using several ML techniques: 

          - Regression: you build a prediction model and you compare the predicted value with the real one. 

          - Clustering: you cluster the data points based on density and data points remaining outside the clusters (outliers) are anomalies.

          - Classification: you need 2 balanced (same size) data-sets (one with normal data points and another with anomalies data points) and you train a classification model to distinguish between them.

          - Statistically: you infer the probability distribution of the data set and any point with a low probability is an anomaly (example: use a normal distribution)

Case study

Text

Problem statement "Short term excessive risk":

 - detect excessive betting risk/activity that Kambi takes in a short period of time

Case study

Text

Problem statement "Short term excessive risk":

 - detect excessive betting risk/activity that Kambi takes in a short period of time.

Solution: apply an aggregation sliding time window. Check if the aggregated result is greater than a pre-defined threshold. 

Case study

Text

Let's slightly change the problem statement :

 - detect suspicious betting risk/activity that Kambi takes in a short period of time.

Case study

Text

Current solution problems:

We may have false positive "suspicious" detection

Case study - sol 1 (simple data transformation)

Text

Why feature engineering is important:

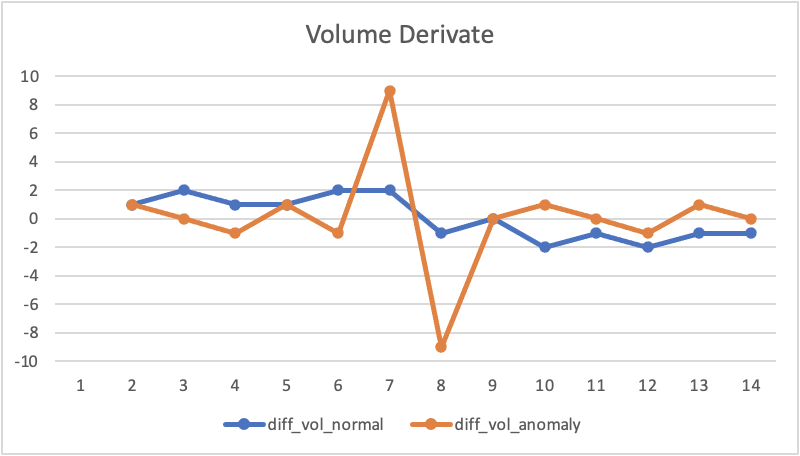
Volume derivate = Volume(t) - Volume(t-1)

Define a threshold for the derivative above which we have an anomaly.

Case study - sol 2 (linear regression on raw data points)

Text

- Divide the last hour into 6 equal time intervals: 0 - 10, 10-20...

- Aggregate the risk taken into each interval.

- Build a linear regression alg to predict the "aggregated risk" in the next time interval (next 10 minutes).

- Compare the predicted value with the real aggregated risk of the next 10 minutes.

- If the difference is too big then we have an anomaly.

So...we have an anomaly detection problem solved with linear regression!

Case study - sol 3 (linear regression on derivatives points)

Text

- Divide the last hour into 6 equal time intervals: 0 - 10, 10-20...

- Aggregate the risk taken into each interval.

- Calculate the derivative for each point (relatively to prev point).

- Build a linear regression alg to predict the "derivative risk" in the next time interval (next 10 minutes).

- Compare the predicted value with the real derivative risk of the next 10 minutes.

- If the difference is too big then we have an anomaly.

As opposed to the last version we will not have problems when the trend is changing (e.g. from ascending to descending)

Case study - sol 3 (linear regression on derivatives points)

Text

Case study - sol 4 (classification)

Text

Pre-requisites: for this solution we need historical data for both anomalies and normal cases, equally sized.

Offline (build model):

- Calculate the historical betting activity for a fixed time interval

- Label each data point as anomaly or normal

- Train a binary classification algorithm

Online (apply model):

- Take the current betting activity in that fixed time interval

- Predict its class using the trained model

Case study - sol 5 (statistically)

Text

Pre-requisites: for this solution we need historical data for normal cases. 

Advantage vs sol 4: we don't need many historical anomaly cases.

Offline (build model):

- Infer from data the probability distribution (usually it is a Gaussian distribution) e.g calculate the mean and standard deviation.

Online (apply model):

- Take the current betting activity in that fixed time interval

- Apply the probability function to get the probability the current point to appear in the distribution

- If the probability is low => we have an anomaly

Summary

Text

• ML problem types: supervised, unsupervised, reinforcement
• A specific optimisation alg (minimize a function) can be used to different classes of ML problems (e.g: gradient descend is used for both linear regression and classification)
• Data transformation and feature engineering is very important
• We can model a problem with different ML techniques...The art is to do this right :) not just writing/choosing an algorithm