De Bruijn

Graphs &

Sequences

Brian Breitsch

Hamilton Path/Cycle

  • a Hamilton path visits each vertex exactly once
    • a Hamilton cycle is a Hamilton path that loops back to the first vertex

Eulerean Path/Cycle

  • an Eulerean path visits each edge exactly once
    • an Eulerean cycle is an Eulerean path that loops back to the first edge

Line Digraph

  • vertices are the edges        of original graph
  •                   when
wx
wx
vw \to xy
vw→xy
w = x
w=x

Example

Nicolaas Govert de Bruijn

  • pronounced 'du bruyn'
  • 9 July 1918 – 17 February 2012
  • analysis, number theory, combinatorics, logic
  • wrote AUTOMATH language in 1960s

De Bruijn Graph

  • alphabet      of size
  •           words of length
  •                   possible words
  • a directed edge exists between       and       when a left shift in the word corresponding to      matches the first            letters of the second word
A
A
|A| = k
∣A∣=k
n
n
v_1
v​1​​
v_2
v​2​​
v_2
v​2​​
k-1
k−1
k^n
k​n​​
0123 \to
0123→
1230
1230
1231
1231
1232
1232
1233
1233
A = \{0, 1, 2, 3\}
A={0,1,2,3}
V =
V=
|V| =
∣V∣=
GdB(k,n)
GdB(k,n)

Another Interpretation

  • digits       of size
  • numbers with      digits
  • vertices are subset of numbers
  • a directed edge exists between       and        when                              for some
S
S
|S| = s
∣S∣=s
k
k
v_1
v​1​​
v_2
v​2​​
v_2 = sv_1 + a
v​2​​=sv​1​​+a
a \in S
a∈S
0123 \times 10 + a\to
0123×10+a→
1230, a = 0
1230,a=0
1231, a = 1
1231,a=1
1232, a = 2
1232,a=2
1233, a = 3
1233,a=3
A = \{0, 1, 2, 3\}
A={0,1,2,3}

Trivial Examples

        ary De Bruijn graph with                is a complete graph

k-
k−
n = 1
n=1

trivial loop graph

|A| = 1 \rightarrow |V| = 1
∣A∣=1→∣V∣=1

diameter

Properties

n
n
\partial GdB(k,n)
∂GdB(k,n)
GdB(k,n)
GdB(k,n)

is balanced (i.e. regular directed graph)

 is strongly connected

is

GdB(k,n)
GdB(k,n)

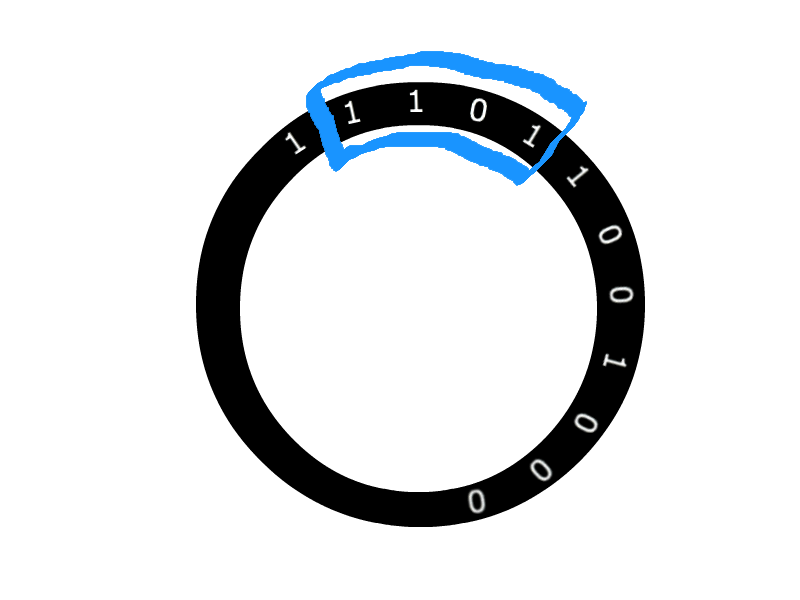
De Bruijn Sequences

A         ary De Bruijn sequence of order     is a cyclic sequence in which every possible word of length     from an alphabet                 appears exactly once.

 

NOTE: sometimes people restrict the definition to a binary alphabet

k-
k−
n
n
|A| = k
∣A∣=k
A = \{0, 1\}
A={0,1}
n = 3
n=3
00010111
00010111

is a De Bruijn sequence

n
n
  • every De Bruijn graph has Euler and Hamliton cycles

Properties

Traversing an Euler/Hamilton cycle yields a De Bruijn Sequence

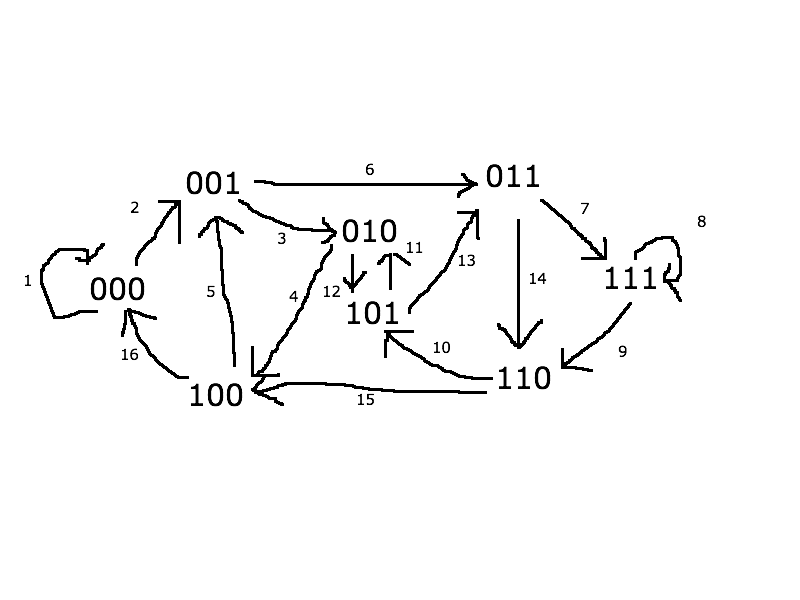
  1. start with complete directed graph
  2. take line graph
  3. repeat     times
n
n

FACT:                        is the line graph of

Properties

GdB(k,n)
GdB(k,n)
GdB(k,n-1)
GdB(k,n−1)

Binary De Bruijn Graphs & Sequences

  •  
  • #edges
  • some can be generated using finite cell automata [9] (maybe?)
    • e.g.
      • the lexigraphically-least sequence is called "grand-daddy"
|V| = 2^n
∣V∣=2​n​​
= 2^{n+1}
=2​n+1​​
00001000110010101111
00001000110010101111

How many binary De Bruijn sequences are there for given n?

GdB(2,n-1)
GdB(2,n−1)
GdB(k,n)
GdB(k,n)

Eulerean tours exist because                      is balanced

This is equivalent to counting the number of Eulerean cycles in

Consider vertices

v,w
v,w
v = (v_1v_2...v_{n-1})
v=(v​1​​v​2​​...v​n−1​​)
w = (w_1w_2...w_{n-1})
w=(w​1​​w​2​​...w​n−1​​)

Then the path from                is

v\to w
v→w
(v_1v_2...v_{n-1})(w_1w_2...w_{n-1})
(v​1​​v​2​​...v​n−1​​)(w​1​​w​2​​...w​n−1​​)
v_1)(v_2...v_{n-1}w_1)(w_2...w_{n-1}
v​1​​)(v​2​​...v​n−1​​w​1​​)(w​2​​...w​n−1​​
v_1v_2)(...v_{n-1}w_1w_2)(...w_{n-1}
v​1​​v​2​​)(...v​n−1​​w​1​​w​2​​)(...w​n−1​​

How many binary De Bruijn sequences are there for given n?

Thus we have exactly one path of length             for any pair of vertices

v,w
v,w
n-1
n−1

This means

A^{n-1} = \left[ 1 \right]
A​n−1​​=[1]

(all 1 matrix)

is the

2^{n-1} \times 2^{n-1}
2​n−1​​×2​n−1​​

adjacency matrix

A
A

The eigenvalues are

\lambda = 0
λ=0
\lambda = 2
λ=2

with multiplicity

with multiplicity

2^{n-1}
2​n−1​​
1
1

How many binary De Bruijn sequences are there for given n?

Matrix-tree theory:

# of Eulerean cycles

= \sum_{e\in E} \kappa (GdB(2,n), e)
=∑​e∈E​​κ(GdB(2,n),e)
= \sum_{e\in E} \frac{\lambda_1 \lambda_2 ... \lambda_{2^{n-1}-1}}{2^{n-1}}
=∑​e∈E​​​2​n−1​​​​λ​1​​λ​2​​...λ​2​n−1​​−1​​​​
= \sum_{e\in E} \frac{2^{2^{n-1}-1}}{2^{n-1}}
=∑​e∈E​​​2​n−1​​​​2​2​n−1​​−1​​​​
= 2^n \frac{2^{2^{n-1}-1}}{2^{n-1}}
=2​n​​​2​n−1​​​​2​2​n−1​​−1​​​​
= 2^{2^{n-1}}
=2​2​n−1​​​​

where

\kappa (GdB(2,n), e)
κ(GdB(2,n),e)

is the vertex connectivity

\kappa (GdB(2,n), e)
κ(GdB(2,n),e)

Applications

  • genomic data storage and processing
    • a De Bruijn graph data structure for genomics compressed a 340GB (naive approach) to under 5GB [1]
\{A, G, T, C\}
{A,G,T,C}
B(4,2)
B(4,2)

Applications

  • fastest way to brute-force attack a number or pad lock that allows uninterrupted input of numbers
...1552537748599...
...1552537748599...

Laundry Machine Dials

  • find the sequence of connections to put on dial for maximum number of consecutive unambiguous options [4]

Indexing 1 in Computer (old)

  • find the location of first 1 in a word using de Bruijn sequences and an efficient hash table lookup [6].
00100000
00100000

multiply by de Bruijn sequence

0000010111000000
0000010111000000
00010111
00010111

mask first byte and shift by 8

00000011
00000011

this is a bijection (because of the property of de Bruijn sequences) and 1 index can thus be looked up in table

Some Open Problems?

Let                          be a subset of a general de Bruijn sequence which contains all sequences of weight between      and

(these are essentially subgraphs of the de Bruijn graph)

GdB_v^w(k,n)
GdB​v​w​​(k,n)
v
v
w
w
  • can these sequences be constructed efficiently
  • what is the first fixed-weight de Bruijn sequence and can it be constructed without "back-tracking"
  • what is the diameter for
GdB_w(k,n)
GdB​w​​(k,n)
GdB_v^w(k,n)
GdB​v​w​​(k,n)

?

References

  1. "Tutorials." Tutorials. Homolog.us – Bioinformatics, 2015. Web. 23 Feb. 2015.
  2. "De Bruijn Graph." Wikipedia. Wikimedia Foundation, n.d. Web. 23 Feb. 2015.
  3. "De Bruijn Sequence." Wikipedia. Wikimedia Foundation, n.d. Web. 23 Feb. 2015.
  4. Higgins, Peter M. Nets, Puzzles, and Postmen: An Exploration of Mathematical Connections. Oxford: Oxford UP, 2009. Print.
  5. Levine, Lionel. "Lecture 21." Algebraic Combinatorics. 28 Apr. 2011. Web.
  6. Leiserson, Charles E., Harold Prokop, and Keith H. Randall. "Using De Bruijn Sequences to Index a 1 in a Computer Word." (1998): n. pag. Web.
  7. Ruskey, Frank, Joe Sawada, and Aaron Williams. "De Bruijn Sequences for Fixed-Weight Binary Strings." SIAM Journal on Discrete Mathematics 26.2 (2012): 605-17. Web.
  8. Shibata, Y., and Y. Gonda. "Extension of De Bruijn Graph and Kautz Graph." Computers & Mathematics with Applications 30.9 (1995): 51-61. Web.
  9. Sutner, Klaus. "De Bruijn Graphs and Linear Cellular Automata." Complex Systems 5 (1991): 19-30. Web.

De Bruijn Graphs & Sequences

By Brian Breitsch

De Bruijn Graphs & Sequences

  • 669

More from Brian Breitsch