GNSS Observations
\rho_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_S
+ b^\rho_{S,f} + b^\rho_{R,f} + I_{S,f} + M^\rho_{S,f} + \epsilon^\rho_{S,f}
\phi_{S,f} = r_S + c\left( \Delta t_s - \Delta t_R \right) + T_s
+ b^\phi_{S,f} + b^\phi_{R,f} - I_{S,f} + \lambda_f N_{S,f} + M^\phi_{S,f} + \epsilon^\phi_{S,f}
HARDWARE
BIAS
IONOSPHERE DELAY
CARRIER
AMBIGUITY
MULTIPATH EFFECTS
FREQUENCY INDEPENDENT EFFECTS
Bias and Error Assumptions
b_{S,f}^\phi \approx b_{S,f}^\rho
b_{R,f}^\phi \approx b_{R,f}^\rho
assume no code-carrier bias
\Delta b_{S,f_i,f_j}, \ \Delta b_{R, f_i, f_j}
- receiver code-carrier bias usually compensated for by manufacturer
since we will use geometry free combinations, we only care about inter-frequency biases
(IFB)
E\left[ M_{f_i} M_{f_j} \right] \approx 0
M^\phi \ll M^\rho
multipath uncorrelated across different signals
carrier pseudorange noise / multipath is small compared to code
not true
\epsilon^\phi \ll \epsilon^\rho
\approx \text{constant}
over 1 day
Geometry-Free Combinations
\phi_{S,f_i} - \phi_{S,f_j} = \Delta b_{S,f_i,f_j} + \Delta b_{R,f_i,f_j} - \left(I_{S,f_i} - I_{S,f_j} \right)
+ \lambda_{f_i}N_{S,f_i} - \lambda_{f_j}N_{S,f_j} + M^\phi_{S,f_i} - M^\phi_{S,f_j} + \epsilon^\phi_{S,f_i} - \epsilon^\phi_{S,f_j}
\rho_{S,f} - \phi_{S,f} \approx 2I_{S,f} - \lambda_fN_{S,f} + M_{S,f}^\rho + \epsilon_{S,f}^{\rho}
\Delta ADR_{f_i,f_j}
CMC_f
Geometry-Free Combinations
We can remove satellite IFB using estimates from IGS
\Delta b_{S,f_i,f_j}
We express ionosphere delays in terms of TEC
\Delta ADR_{f_i,f_j} \approx \Delta b_{R,f_i,f_j} - \frac{40.3\times 10^{16}}{\alpha_{f_i,f_j}}TEC
+ \lambda_{f_i} N_{S,f_i} - \lambda_{f_j} N_{S,f_j} + \cdots
CMC_f \approx \frac{40.3\times 10^{16}}{f^2}TEC - \lambda_f N_{S,f} + \cdots
multipath / noise / unmodeled errors
ILS TEC Estimation
Use iterative least-squares to solve large sparse system for 1 day of data
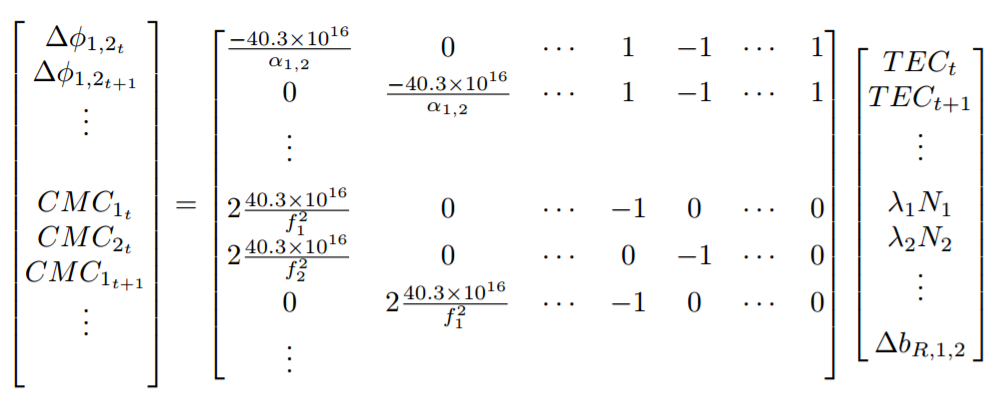
Example of 2-Frequency TEC From Velox LEO Satellite
before algorithm
after algorithm
2016-01-24
Backup-Slides Batch Dual-Frequency TEC Estimation
By Brian Breitsch
