Linear Combinations of GNSS Phase Observables
Brian Breitsch
Advisor: Jade Morton
Committee: Charles Rino, Anton Betten
to Improve and Assess TEC Estimation Precision
Background and Motivation
Linear Estimation of GNSS Parameters
TEC Estimate Error Residuals
Application to Real GPS Data
Earth's Ionosphere
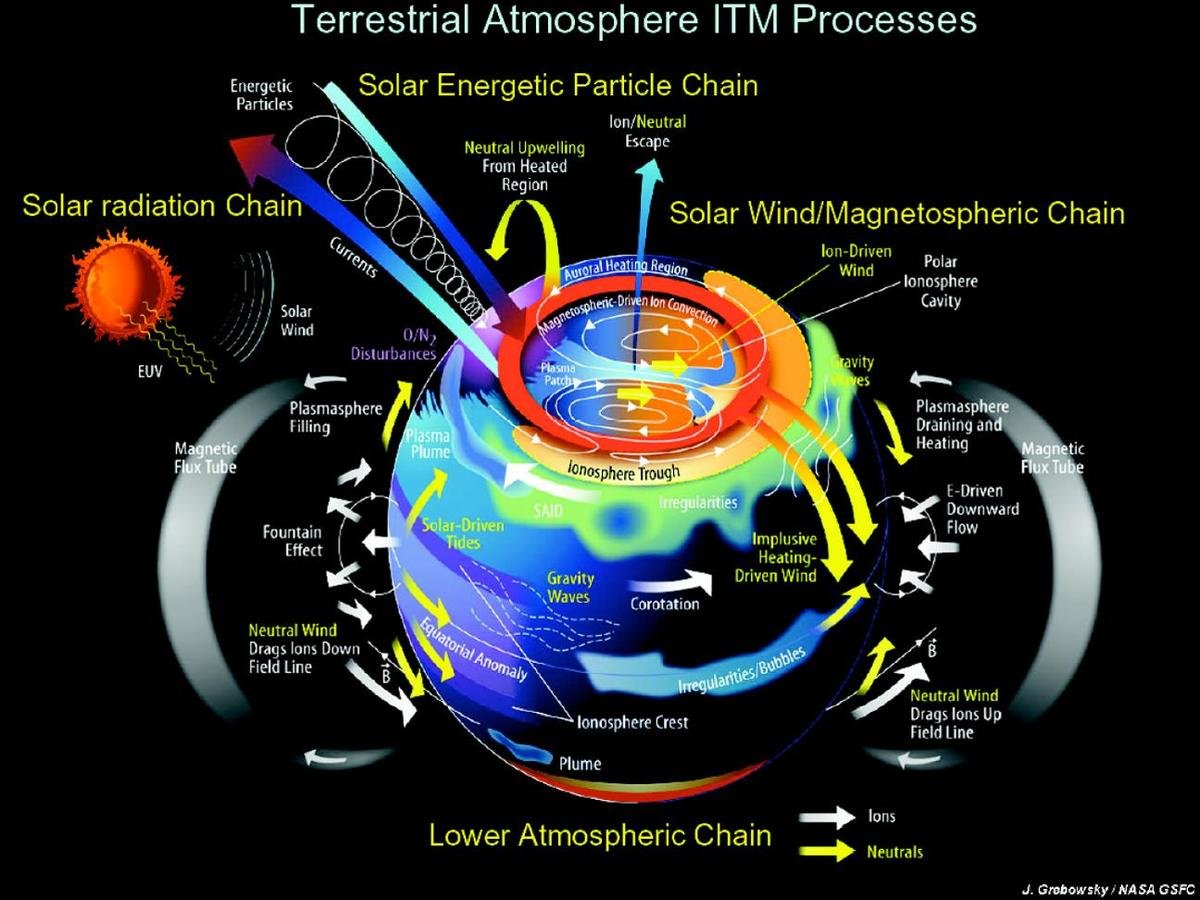
J. Grobowsky / NASA GSFC
Ionosphere Effects on Electromagnetic Propagation
ionosphere = cold, collisionless, magnetized plasma
for L-band frequencies (1-2 GHz) refractive index given by:
n = 1 - \frac{1}{2} X \pm \frac{X|Y\cos\theta_B|}{2} - \frac{1}{8}X^2 \pm \mathcal{O}(\frac{1}{f^5})
\(f\) = wave frequency
\(N_e\) = plasma density
\(\epsilon_0\) = permittivity of free space
\(e\) = fundamental charge
\(m\) = electron rest mass
\(B_0\) = ambient magnetic field strength
X = \frac{\omega_p^2}{\omega^2} \kern{1em}
Y = \frac{\omega_H}{\omega} \kern{1em}
\omega = 2 \pi f \kern{1em}
\omega_p = \sqrt{\frac{N_e e^2}{\epsilon_0 m}} \kern{1em}
\omega_H = \sqrt{\frac{B_0 |e|}{m}}
radio source
ionosphere
phase shift / distortion
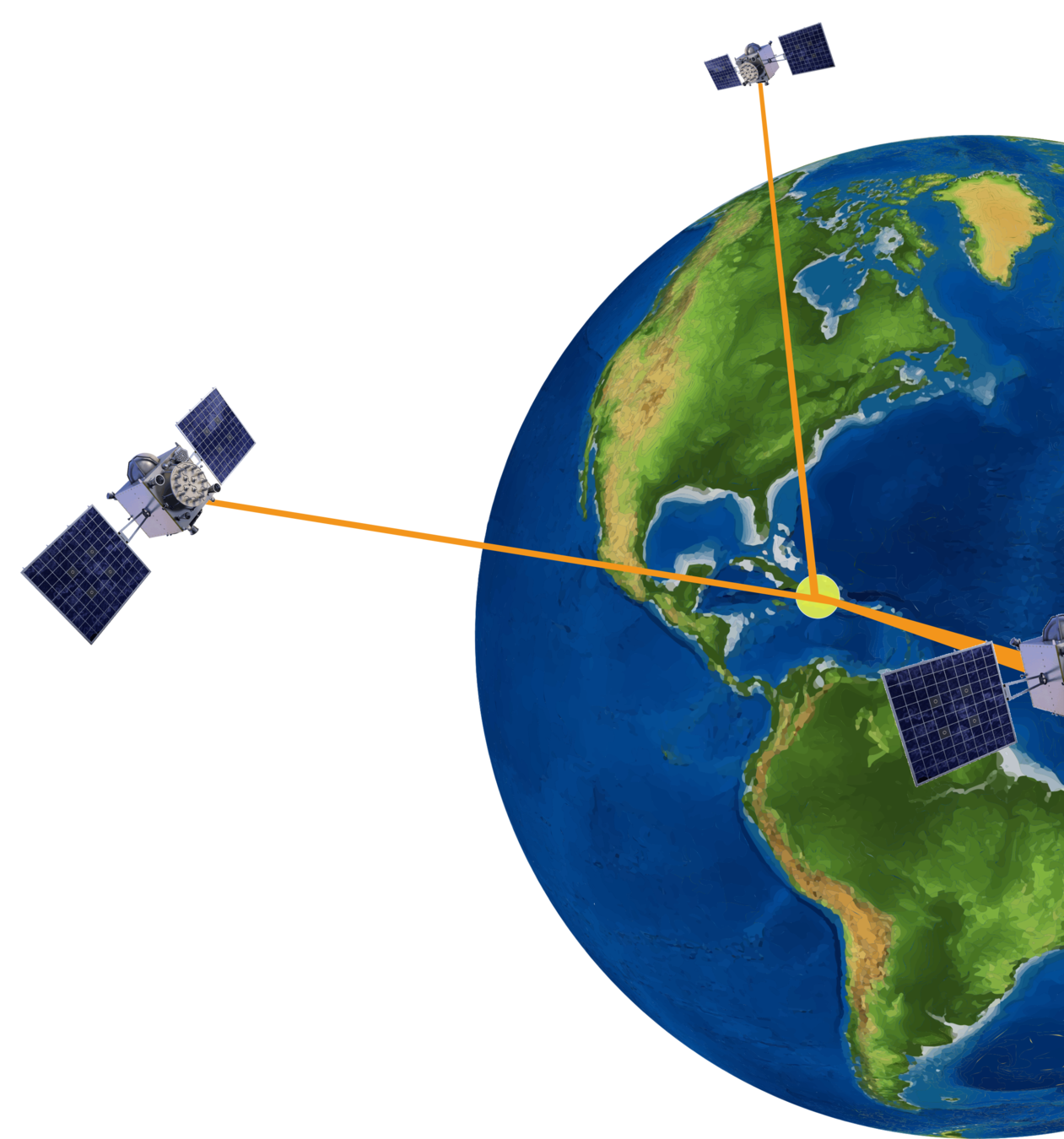
Global Navigation Satellite Systems (GNSS)
...a useful everyday radio source for geophysical remote-sensing!
GPS
GLONASS
Beidou
Galileio
...etc.
GPS - Global Positioning System
- 32-satellite constellation
- transmit dual-frequency BPSK-moduled signals
- new Block-IIF and next-gen Block-III satellites transmitting triple-frequency signals
| Signal | Frequency (GHz) |
|---|---|
| L1CA | 1.57542 |
| L2C | 1.2276 |
| L5 | 1.17645 |
GNSS Carrier Phase Observable
\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
HARDWARE BIAS
IONOSPHERE RANGE ERROR
CARRIER AMBIGUITY
SYSTEMATIC ERRORS / MULTIPATH
FREQUENCY INDEPENDENT EFFECTS
STOCHASTIC ERRORS
accumulated phase (in meters) of demodulated GNSS signal at receiver for a particular satellite and signal carrier frequency \(f_i\)
Ionosphere Range Error
consider first-order term in ionosphere refractive index
second and higher-order terms on the order of a few cm
I_i = \displaystyle \int_\text{rx}^\text{tx} n - 1 \ ds
\approx -\frac{\kappa}{f_i^2} \displaystyle \int_\text{rx}^\text{tx} N_e \ ds
n \approx 1 - \frac{1}{2} X = 1-\frac{\kappa}{f_i^2} N_e
\kappa = \frac{e^2}{8\pi^2\epsilon_0 m_e} \approx 40.301
TOTAL ELECTRON CONTENT
rx
tx
plasma / free electrons
units: \(\frac{\text{electrons}}{\text{m}^2}\)
often measured in TEC units:
1 \text{TECu} = 10^{16} \frac{\text{electrons}}{\text{m}^2}
Ionosphere Plasma Density
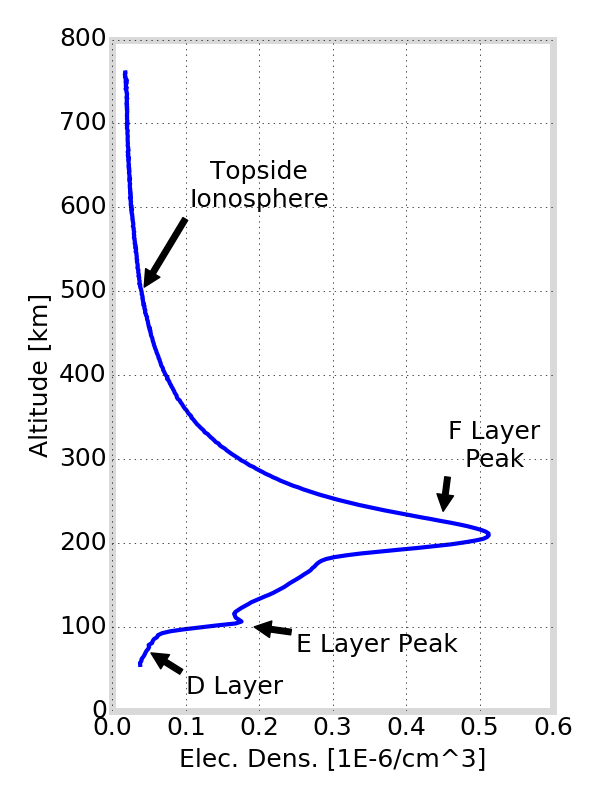
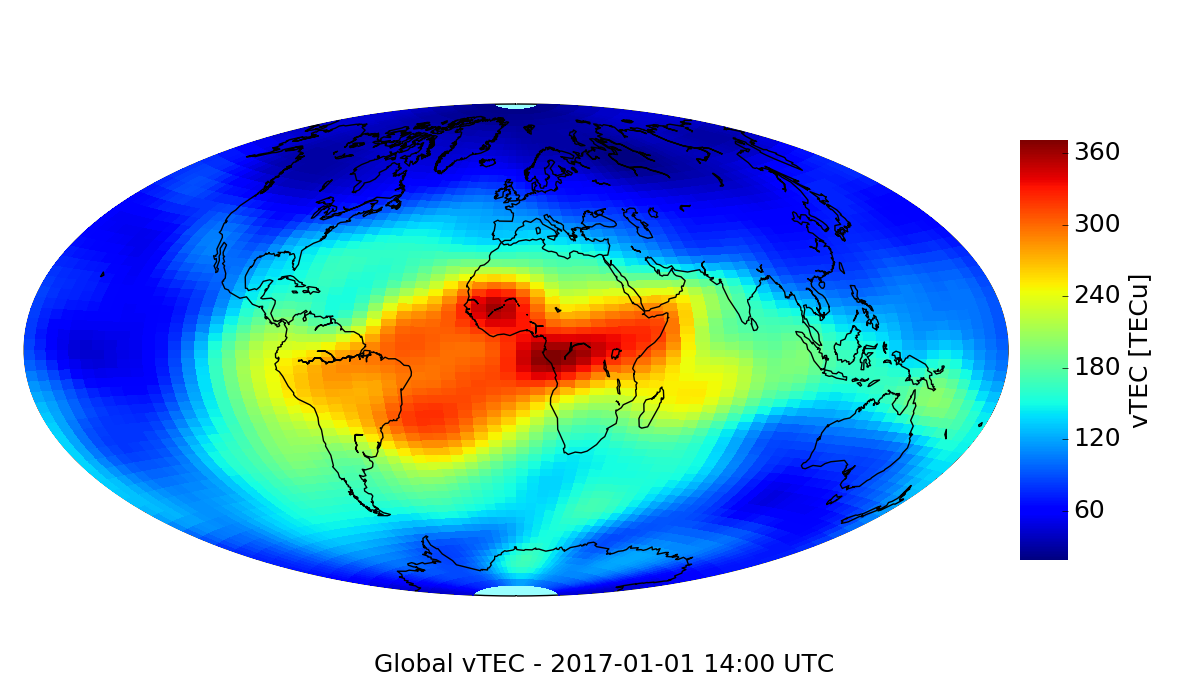
TEC and vertical TEC (vTEC) used to image plasma density structures
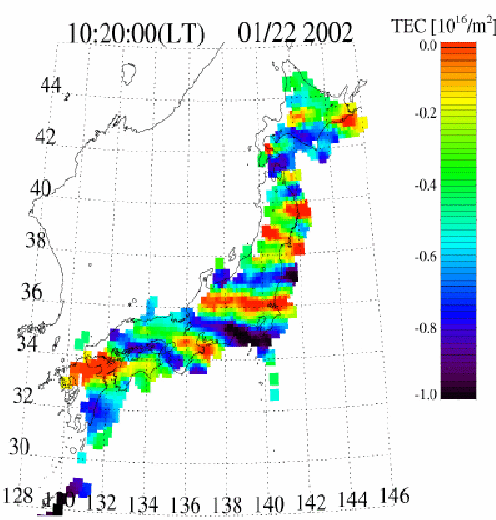
profile from CDAAC
image from Saito et al.
map from IGS
vertical distribution
horizontal distribution
travelling ionosphere disturbances (TIDs)
TEC
vTEC
TEC Estimation Using Dual-Frequency GNSS
\Phi_1 - \Phi_2 = \left(I_1 - I_2\right) + \left(\lambda_1 N_1 - \lambda_2 N_2\right) + \left(H_1 - H_2\right)
\approx -\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right) \text{TEC} + \left(\lambda_1 N_1 - \lambda_2 N_2\right) + \Delta H_{1,2}
satellite and receiver inter-frequency hardware biases
neglecting systematic and stochastic error terms:
after resolving bias terms:
\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
carrier ambiguities
bias terms
Resolving Bias Terms
-
LAMBDA
-
code-carrier-levelling
carrier ambiguity resolution
hardware bias estimation
-
must apply ionosphere model
- e.g. global ionosphere model using data assimilation and receiver networks
- e.g. single receiver and linear 2D-gradient in vTEC (applied in Bourne 2016 [2])
Examples of Dual-Frequency TEC Estimates
Poker Flat, Alaska, 2016-01-02
Using methods similar to [2] and [3] to solve for bias terms, we compute dual-frequency TEC estimate \(\text{TEC}_\text{L1,L2}\) and \(\text{TEC}_\text{L1,L5}\)
\(\text{TEC}_{\text{L1,L5}} - \text{TEC}_{\text{L1,L2}}\)
Poker Flat, Alaska, 2016-01-02
Can we characterize / find the source of these discrepancies?
Can we relate them to errors in dual-frequency TEC estimates?
Objectives
Investigate the discrepancy in \(\text{TEC}_\text{L1,L5} - \text{TEC}_\text{L1,L2}\)
Derive optimal triple-frequency estimation of TEC
Provide a (partial) characterization of TEC estimate residual errors
Motivation
-
Push the boundaries of TID signature detection from earthquakes, explosions, etc.
-
Understand / address the errors in TEC estimates from low-elevation satellites
-
Improve user range error for precise positioning applications
Improve / understand TEC estimate precision
Approach
Apply framework to derive triple-frequency estimates of TEC and systematic errors
Develop framework for linear estimation of GNSS parameters
Relate to impact on TEC estimate error residuals
Background and Motivation
Linear Estimation of GNSS Parameters
TEC Estimate Error Residuals
Application to Real GPS Data
Simplified Carrier Phase Model
\Phi_i = G + I_i + S_i + \epsilon_i
zero-mean
normally-
distributed
zero-mean
neglect bias terms
By neglecting bias terms, we address estimation precision, rather than accuracy
\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
"geometry" term
model parameters
\mathbf{\Phi} = \left[\Phi_1, \cdots, \Phi_m\right]^T
\mathbf{m} = \left[G, \text{TEC}, S_1, \cdots, S_m \right]^T
\mathbf{A} = \begin{bmatrix}
1 & -\frac{\kappa}{f_1^2} & 1 & 0 & \cdots & 0 \\
1 & -\frac{\kappa}{f_2^2} & 0 & 1 & \cdots & 0 \\
\vdots & & & & \ddots & \\
1 & -\frac{\kappa}{f_m^2} & 0 & \cdots & & 1
\end{bmatrix}
\mathbf{\epsilon} = [\epsilon_1, \cdots, \epsilon_m]^T
\mathbf{\Phi} = \mathbf{A} \mathbf{m} + \mathbf{\epsilon}
Linear Inverse Problem
observations
stochastic error
forward model
Linear Estimation
\mathbf{\hat{m}}
\mathbf{A^*} = \ ?
\mathbf{\hat{m}} \approx \mathbf{A^*} \mathbf{\Phi}
\mathbf{A}^T \left(\mathbf{A}\mathbf{A}^T\right)^{-1}
Poor results; treats each parameter with equal weight
We must apply a priori information about model parameters
model estimate
model estimator
A Priori Information
|G| \gg |I_i| \gg |S_i|
Under normal conditions, we know that:
G \sim
I \sim
S \sim
20,000 km
1 - 150 m
several cm
Using A Priori Information
We could apply \(|G| \gg |I_i| \gg |S_i|\) using Gaussian priors
Instead we derive each row separately:
\mathbf{A^*} =\begin{bmatrix}
\mathbf{C}_G \\
\mathbf{C}_\text{TEC} \\
\mathbf{C}_{S_1} \\
\vdots \\
\mathbf{C}_{S_m}
\end{bmatrix}
geometry estimator
TECu estimator
systematic-error estimators
estimator
\mathbf{C} = \left[c_1, \cdots, c_m \right]^T \in \mathbb{R}^m
(written as row vectors here)
How to Choose Optimal \(\mathbf{C}\)
Goals:
1. produce desired parameter with unity coefficient
2. remove / reduce all other terms
Linear combination \(E\) given by inner-product:
E = \langle \mathbf{C} | \mathbf{\Phi} \rangle
Approach:
First, constrain \(\mathbf{C}\) to satisfy Goal 1
Then, constrain / optimize \(\mathbf{C}\) to achieve Goal 2
Linear Coefficient Constraints
Use one or two of the following constraints to reduce search space for optimal estimator coefficients:
\sum_i c_i = 0
\sum_i c_i = 1
geometry-free
geometry-estimator
\sum_i -\frac{\kappa}{f_i^2}c_i = 1
\sum_i \frac{c_i}{f_i^2} = 0
TEC-estimator
ionosphere-free
\Phi_i = G + I_i + S_i + \epsilon_i
Reduction of Error
\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \mathbf{C}^T \Sigma_\epsilon \mathbf{C}
Linear combination stochastic error variance:
\sigma_\epsilon^2 = \mathbf{C}^T \mathbf{\Sigma}_\epsilon \mathbf{C}
where \(\mathbf{\Sigma}_\epsilon\) is the covariance matrix between \(\mathbf{\epsilon}_i\)
Optimal \(\mathbf{C}\) for minimizing stochastic error variance:
\(\epsilon_i\) equal-amplitude and uncorrelated
\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2
TEC Estimator
1. apply TECu-estimator constraint
2. apply geometry-free constraint (since \(|G| \gg |I_i|\) )
Dual-Frequency Example
\Rightarrow c_1 = \displaystyle -\frac{1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
\begin{aligned}
& -\frac{\kappa}{f_1^2}c_1 - \frac{\kappa}{f_2^2}c_2 = 1 \\[1em]
& c_1 + c_2 = 0 \Rightarrow c_1 = -c_2 \\[1em]
\Rightarrow & -\kappa c_1 \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right) = 1
\end{aligned}
TEC-estimator
geometry-free
recall:
\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
Triple-Frequency TEC Estimator
Applying constraints yields following system of coefficients (with free parameter denoted \(x\):
\begin{aligned}
c_1 &= \frac{\frac{1}{\kappa} + x \left( \frac{1}{f_3^2} - \frac{1}{f_2^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em]
c_2 &= \frac{-\frac{1}{\kappa} - x \left( \frac{1}{f_3^2} - \frac{1}{f_1^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}}
\\[1em]
c_3 & = \ \ x
\end{aligned}
x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}
To satisfy \( \mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2 \), choose
denote corresponding coefficient vector \(\mathbf{C}_{\text{TEC}_{1,2,3}}\) and its corresponding estimate \(\text{TEC}_{1,2,3}\)
TEC Estimator Using Triple-Frequency GPS
\begin{matrix}
\text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em]
\text{TEC}_\text{L1,L2,L5} & 8.294 & -2.883 & -5.411 & 10.314 & \\
\text{TEC}_\text{L1,L5} & 7.762 & 0 & -7.762 & 10.977 & \\
\text{TEC}_\text{L1,L2} & 9.518 & -9.518 & 0 & 13.460 & \\
\text{TEC}_\text{L2,L5} & 0 & 42.080 & -42.080 & 59.510 &
\end{matrix}
\mathbf{C}_{\text{TEC}_\text{L1,L2,L5}}
\mathbf{C}_{\text{TEC}_\text{L1,L5}}
\mathbf{C}_{\text{TEC}_\text{L1,L2}}
\mathbf{C}_{\text{TEC}_\text{L2,L5}}
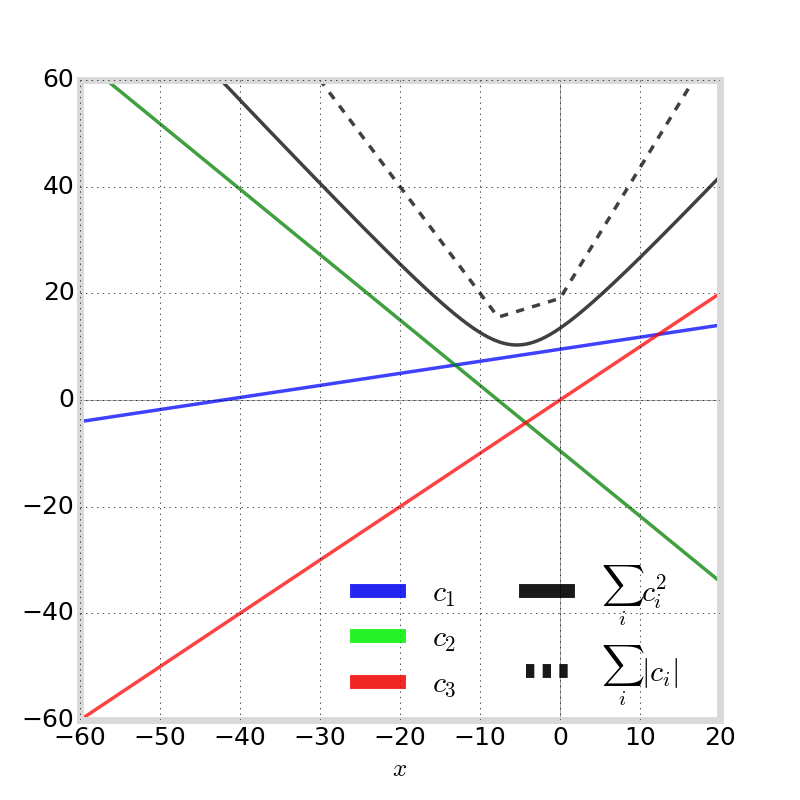
Geometry Estimator
\begin{matrix}
c_1 = & \frac{-\frac{1}{f_2^2} + x \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\
c_2 = & \frac{\frac{1}{f_1^2} - x \left(\frac{1}{f_1^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\
c_3 = & x
\end{matrix}
For triple-frequency GNSS:
1. apply geometry-estimator constraint
2. apply ionosphere-free constraint since \(I_i\) are the next-largest terms
x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}
To satisfy \( \mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2 \),
We call this coefficient vector \(\mathbf{C}_{G_{1,2,3}}\) and its corresponding estimate \(G_{1,2,3}\)
the optimal "ionosphere-free combination"
Geometry Estimator Using Triple-Frequency GPS
\begin{matrix}
\text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em]
G_\text{L1,L2,L5} & 2.327 & -0.360 & -0.967 & 2.546 \\
G_\text{L1,L5} & 2.261 & 0 & -1.261 & 2.588 \\
G_\text{L1,L2} & 2.546 & -1.546 & 0 & 2.978 \\
G_\text{L2,L5} & 0 & 12.255 & -11.255 & 16.639
\end{matrix}
\mathbf{C}_{G_\text{L1,L2,L5}}
\mathbf{C}_{G_\text{L1,L5}}
\mathbf{C}_{G_\text{L1,L2}}
\mathbf{C}_{G_\text{L2,L5}}
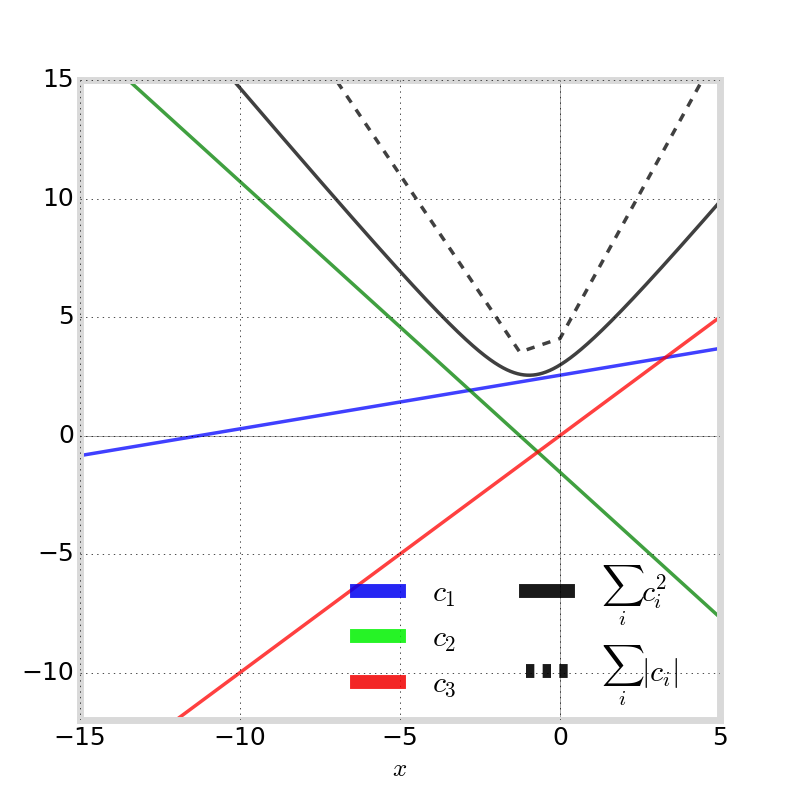
Systematic Error Estimator
Since \(|G| \gg |I_i| \gg |S_i|\), must apply both geometry-free and ionosphere-free constraints
For triple-frequency GNSS:
\begin{aligned}
c_1 & = \ \ x \frac{\frac{1}{f_3^2} - \frac{1}{f_2^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em]
c_2 & = - x \frac{\frac{1}{f_3^2} - \frac{1}{f_1^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em]
c_3 & = \ \ x
\end{aligned}
system is linear subspace
there is "only one" estimate of systematic errors
note this requires \(m \ge 3\)
Geometry-Ionosphere-Free Combination
We call the linear combination that applies both geometry-free and ionosphere-free constraints the geometry-ionosphere-free combination (GIFC)
FACT: The difference between any two TEC estimates produces some scaling of the GIFC
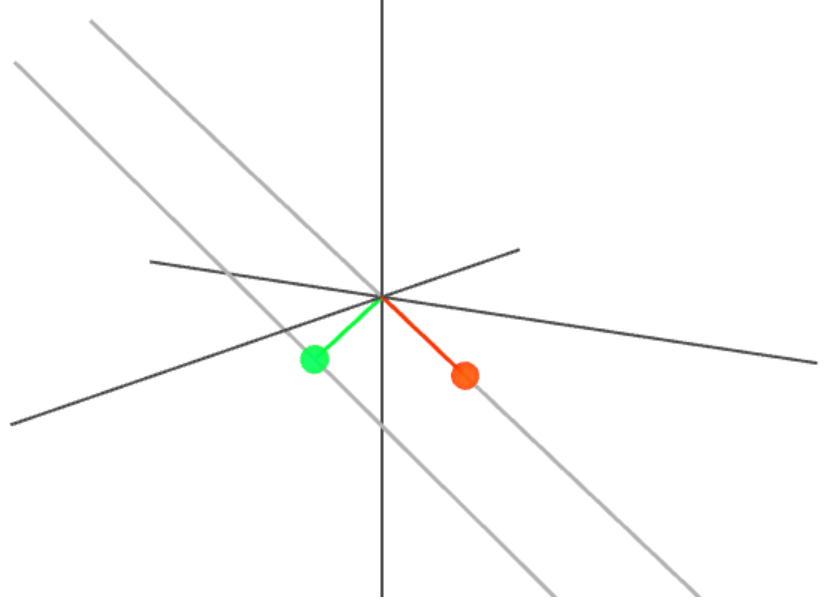
FACT: \(\mathbf{C}_\text{GIFC}\) and \(\mathbf{C}_{\text{TEC}_{1,2,3}}\) are perpendicular, i.e.
\langle \mathbf{C}_\text{GIFC} | \mathbf{C}_{\text{TEC}_{1,2,3}} \rangle = 0
FACT:
\frac{\langle \mathbf{C}_\text{TEC} | \mathbf{C}_{\text{TEC}_{1,2,3}} \rangle}{|| \mathbf{C}_{\text{TEC}_{1,2,3}} ||} = || \mathbf{C}_{\text{TEC}_{1,2,3}} ||
i.e. \(\mathbf{C}_\text{TEC} \) projected onto direction \(\mathbf{C}_{\text{TEC}_{1,2,3}}\) lands at \(\mathbf{C}_{\text{TEC}_{1,2,3}} \)
\mathbf{C}_{\text{TEC}_{1,2,3}}
\mathbf{C}_\text{GIFC}
GIFC Triple-Frequency GPS
\begin{aligned}
\mathbf{C}_{\text{GIFC}_\text{L1,L2,L5}} & = \mathbf{C}_{\text{TEC}_{\text{L1,L5}}} - \mathbf{C}_{\text{TEC}_{\text{L1,L2}}} \\[1em]
& = \left[-1.756, 9.520, -7.764\right]^T
\end{aligned}
We (arbitrarily) choose:
Note: the triple-frequency GIFC does not have a well-defined unit.
GIFC in our results section have the scaling shown here.
Background and Motivation
Linear Estimation of GNSS Parameters
TEC Estimate Error Residuals
Application to Real GPS Data
Estimate Residual Error
Define the error residual vector \(\mathbf{R}\) with components:
The residual error impacting the TEC estimate is:
R_{\text{TEC}} = \langle \mathbf{C}_{\text{TEC}} | \mathbf{R} \rangle
\text{GIFC} = \langle \mathbf{C}_{\text{GIFC}} | \mathbf{R} \rangle
Note that:
R_i = S_i + \epsilon_i
A Convenient Basis
We transform \(\mathbf{R}\) using the orthonormal basis:
\mathbf{U}_1 = \frac{\mathbf{C}_{\text{TEC}_{1,2,3}}}{||\mathbf{C}_{\text{TEC}_{1,2,3}}||}
\mathbf{U}_2 = \frac{\mathbf{C}_\text{GIFC}}{||\mathbf{C}_\text{GIFC}||}
\mathbf{U}_3 = \mathbf{U}_1 \times \mathbf{U}_2
\mathbf{U} = \begin{bmatrix} \mathbf{U}_1 \\ \mathbf{U}_2 \\ \mathbf{U}_3 \end{bmatrix}
\mathbf{R}' = \mathbf{U} \mathbf{R}
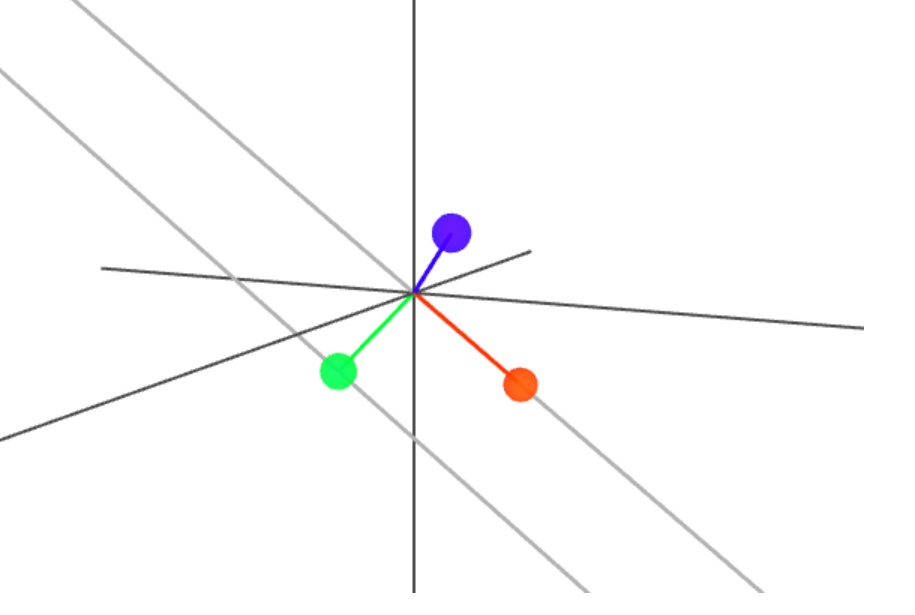
Note that \(\mathbf{U}_3 \perp \mathbf{C}_\text{TEC} \) since \(\mathbf{U}_1\) and \(\mathbf{U}_2\) span the geometry-free plane
R_i' = \langle \mathbf{U}_i | \mathbf{R} \rangle
R_1' = \frac{R_{\text{TEC}_{1,2,3}}}{||\mathbf{C}_{\text{TEC}_{1,2,3}}||}
R_2' = \frac{\text{GIFC}}{||\mathbf{C}_\text{GIFC}||}
Note that:
TEC Estimate Residual Error
common TEC estimate residual error component
GIFC residual error component
\begin{aligned}
R_\text{TEC} & = \langle \mathbf{U} \mathbf{C}_\text{TEC} | \mathbf{U} \mathbf{R} \rangle \\[1em]
& = \langle \mathbf{U}_1 | \mathbf{C}_\text{TEC} \rangle R_1' + \langle \mathbf{U}_2 | \mathbf{C}_\text{TEC} \rangle R_2' \\[1em]
& = R_{\text{TEC}_{1,2,3}} + \frac{\langle \mathbf{C}_\text{GIFC} | \mathbf{C}_\text{TEC} \rangle}{||\mathbf{C}_\text{GIFC}||^2} R_\text{GIFC}
\end{aligned}
Express \(R_\text{TEC}\) as residual error components in transformed coordinate system:
\mathbf{U}_1 = \frac{\mathbf{C}_{\text{TEC}_{1,2,3}}}{||\mathbf{C}_{\text{TEC}_{1,2,3}}||}
\mathbf{U}_2 = \frac{\mathbf{C}_\text{GIFC}}{||\mathbf{C}_\text{GIFC}||}
\langle \mathbf{U}_3 | \mathbf{C}_\text{TEC} \rangle = 0
TEC Estimate Residual Error Discussion
Term \( \frac{\langle \mathbf{C}_\text{GIFC} | \mathbf{C}_\text{TEC} \rangle}{||\mathbf{C}_\text{GIFC}||^2} \) = amplitude of GIFC residual error component in TEC estimate
Term \(R_{\text{TEC}_{1,2,3}}\) = unobservable "TEC-like" residual error component
\(\text{TEC}_{1,2,3}\) is optimal in the sense that it completely removes the GIFC component of residual error
But can we say anything about the overall TEC estimate residual error?
Argument for Using GIFC to Assess Overall Residual Error
Assume \(\mathbf{R}\) has an overall distribution that is joint symmetric about the origin with distribution function \(f_R(x)\)
The distribution of a scaled version \(a \mathbf{R}\) for some scalar \(a\) is \(f_R (\frac{x}{a})\)
By definition, \(\mathbf{U}\mathbf{R} \sim \) symmetric with \(f_R(x) \) for any orthonormal transformation \(\mathbf{U}\)
\(R_i\) equal amplitude and uncorrelated
f_{R_\text{TEC}}(x) = f_{R}\left( \frac{x}{||\mathbf{C}_\text{TEC} ||} \right)
f_\text{GIFC}(x) = f_{R}\left( \frac{x}{||\mathbf{C}_\text{GIFC} ||} \right)
f_{R_\text{TEC}} (x) = f_\text{GIFC}\left( \frac{||\mathbf{C}_\text{GIFC}||}{||\mathbf{C}_\text{TEC} ||} x \right)
Overall TEC Residual Error Discussion
The assumption that \(\mathbf{R}\) has joint symmetric distribution is wrong
We can do better by carefully assessing a priori knowledge about the error components in each \(\Phi_i\)
- this is a lot of work
- investigating GIFC is first-step in this process
\(f_{R_\text{TEC}}(x) = f_\text{GIFC} \left(\frac{||\mathbf{C}_\text{GIFC}||}{||\mathbf{C}_\text{TEC}||} x \right) \) is a coarse approximation
- relates deviations as: \(\text{dev} R_\text{TEC} \approx \frac{||\mathbf{C}_\text{TEC}||}{||\mathbf{C}_\text{GIFC}||} \text{dev} \ \text{GIFC} \)
- could be very wrong if \(R_{\text{TEC}_{1,2,3}} \gg GIFC \)
Relation Between GIFC and TEC Estimate Residual Errors
\begin{matrix}
\text{Estimate} & \frac{\langle \mathbf{C}_\text{GIFC} | \mathbf{C}_\text{TEC} \rangle}{||\mathbf{C}_\text{GIFC}||^2} & \frac{||\mathbf{C}_\text{TEC}||}{||\mathbf{C}_\text{GIFC}||} \\
\text{TEC}_\text{L1,L2,L5} & 0 & 0.831 \\
\text{TEC}_\text{L1,L5} & 0.303 & 0.885 \\
\text{TEC}_\text{L1,L2} & -0.697 & 1.085 \\
\text{TEC}_\text{L2,L5} & 4.723 & 4.796
\end{matrix}
amplitude of GIFC error signal in TEC residual
relates deviation in GIFC and TEC residual
Background and Motivation
Linear Estimation of GNSS Parameters
TEC Estimate Error Residuals
Application to Real GPS Data
Experiment Data
GPS Lab high-rate GNSS data collection network
- Alaska, Hong Kong, Peru
- 2013, 2014, 2015, 2016
- Septentrio PolarXs
- 1 Hz GPS L1/L2/L5 measurements
Data Alignment
-
align data by sidereal day
- 23h 56m 4.1s
-
level GIFC by one of two methods:
- subtract overall GIFC mean
- subtract GIFC mean near (5 minute window) highest-elevation epoch
GPS orbital period \(\approx\) 1/2 sidereal day
Examples
Method 1
Method 2
Data Jump Correction
- jumps in carrier phase due to ionosphere activity, multipath, etc.
-
remove jumps in GIFC
- detect large jumps in epoch-to-epoch GIFC difference
- simultaneously estimate polynomial fit and jump amplitude
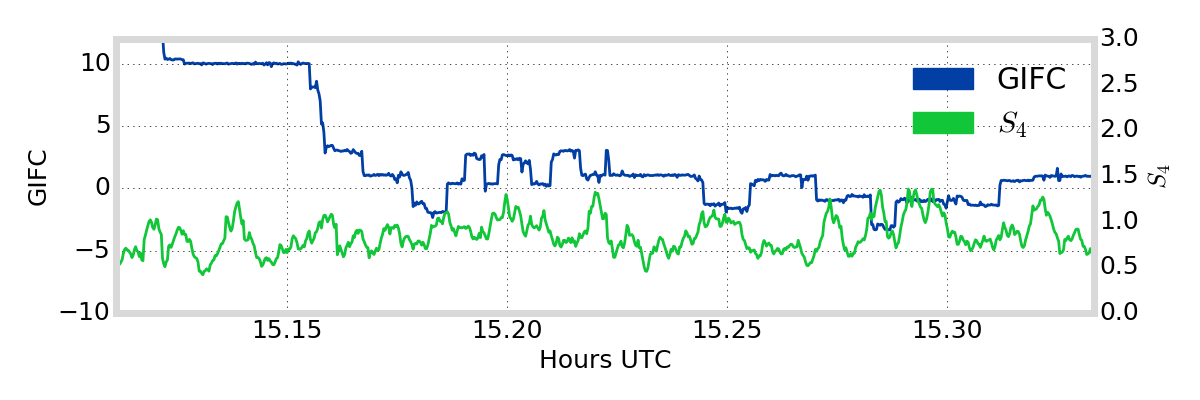
Example of significant GIFC jumps for which the method failed
GIFC Examples
Alaska
method 1 levelling
GIFC Examples
Hong Kong
method 1 levelling
GIFC Examples
Peru
method 1 levelling
GIFC Calendar
Alaska
method 2 levelling
GIFC Calendar
Hong Kong
method 2 levelling
GIFC Calendar
Peru
method 2 levelling
GIFC Heatmap
Alaska
method 1 levelling
GIFC Heatmap
Hong Kong
method 1 levelling
GIFC Heatmap
Peru
method 1 levelling
GIFC Deviations and TEC Residual Error Estimates
\begin{matrix}
\text{Percentile} & \text{GIFC Deviation} \\
50 & 0.11 \\
75 & 0.19 \\
90 & 0.21 \\
\end{matrix}
\begin{matrix}
\text{Percentile} & \kern{5em} & \text{TEC}_\text{L1,L5} & \text{TEC}_\text{L1,L2} & \text{TEC}_\text{L2,L5} \\
50 & & 0.033 & 0.077 & 0.520 \\
75 & & 0.058 & 0.132 & 0.897 \\
90 & & 0.064 & 0.146 & 0.992
\end{matrix}
\begin{matrix}
\text{Percentile} & \text{TEC}_\text{L1,L2,L5} & \text{TEC}_\text{L1,L5} & \text{TEC}_\text{L1,L2} & \text{TEC}_\text{L2,L5} \\
50 & 0.091 & 0.097 & 0.119 & 0.528 \\
75 & 0.158 & 0.168 & 0.206 & 0.911 \\
90 & 0.175 & 0.186 & 0.228 & 1.007
\end{matrix}
\frac{\langle \mathbf{C}_\text{GIFC} | \mathbf{C}_\text{TEC} \rangle}{||\mathbf{C}_\text{GIFC}||^2}
\frac{||\mathbf{C}_\text{TEC}||}{||\mathbf{C}_\text{GIFC}||}
GIFC deviation multiplied by scaling factor
Conclusions
- introduced simplified GNSS carrier phase observation model
- introduced methodology to choose linear combination coefficients for TEC and geometry estimators
- derived GIFC for triple-frequency GNSS
- characterized the GIFC
- showed long-term calendar analysis
- showed percentile deviations over all data
- related deviations to TEC error residual estimates
Acknowledgements
This research was supported by the Air Force Research Laboratory and NASA.
References
[1] Saito A., S. Fukao, and S. Miyazaki, High resolution mapping of TEC perturbations with the GSI GPS network over Japan, Geophys. Res. Lett., 25, 3079-3082, 1998.
[2] Bourne, Harrison W. An algorithm for accurate ionospheric total electron content and receiver bias estimation using GPS measurements. Diss. Colorado State University. Libraries, 2016.
[3] Spits, Justine. Total Electron Content reconstruction using triple frequency GNSS signals. Diss. Université de Liège, Belgique, 2012.
Copy of Optimal Linear Combinations of GNSS Phase Observables to Improve and Assess TEC Estimation Precision
By Brian Breitsch
