排序(Sort)
10^11
目錄
- 泡沫排序 Bubble Sort
- 補充教材

- 選擇排序 Selection Sort
- 插入排序 Insertion Sort
排序演算法(Sorting algorithm)
先來talk talk 什麼是排序演算法
排序演算法(Sorting algorithm)
一種能將一串資料依照特定排序方式排列的演算法
其中,有六個較為常見的排序方式:
1.泡沫排序(Bubble Sort)
2.插入排序(Insertion Sort)
3.選擇排序(Selection Sort)
4.快速排序(Quick Sort)
5.合併排序(Merge Sort)
6.堆排序(Heap Sort)
排序演算法(Sorting algorithm)
穩定排序法(stable sorting):
如果鍵值相同之資料,在排序後相對位置與排序前相同時,稱穩定排序
eg:
3,1,3*,6 -> 1,3,3*,6
不穩定排序法(unstable sorting):
如果鍵值相同之資料,在排序後相對位置與排序前不相同時,稱不穩定排序。
eg:
3,1,3*,6 -> 1,3*,3,6
排序演算法(Sorting algorithm)
排序演算法(Sorting algorithm)

泡沫排序(Bubble Sort)
它重複地走訪要排序的數列,一次比較兩個元素,如果它們的順序錯誤就把它們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。
這個演算法的名字由來是因為越小的元素會經由交換慢慢「浮」到數列的頂端。
它重複地走訪要排序的數列,一次比較兩個元素,如果它們的順序錯誤就把它們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。
這個演算法的名字由來是因為越小的元素會經由交換慢慢「浮」到數列的頂端。
為穩定排序法。
泡沫排序(Bubble Sort)
這個演算法是最簡單瞭解和實作的排序演算法之一,
但它對於包含大量的元素的數列排序是很沒有效率的。

它和這隻生物不同,
它需要花很多時間才能完成
泡沫排序(Bubble Sort)
步驟說明:
- 1.比較相鄰的元素。如果第一個比第二個大,就交換它們兩個。
- 2.對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。
- 這步做完後,最後的元素會是最大的數。
- 3.針對所有的元素重複以上的步驟,除了最後一個。
- 4.持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
泡沫排序(Bubble Sort)
1
2
3
4
5
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
4
5
3
2
1
泡沫排序(Bubble Sort)
程式碼(函式&詳細交換版本)
#include <bits/stdc++.h>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
// 交換arr[j]和arr[j+1]
int x = arr[j];
arr[j] = arr[j+1];
arr[j+1] = x;
}
}
}
}
int main() {
int arr[] = {5,4,3,2,1};
int n = 5;
cout << "原始數列:";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
bubbleSort(arr, n);
cout << "排序後數列:";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}泡沫排序(Bubble Sort)
起飛喜歡把數字排成一列
他首先先看個位數,把個位數由小到大排
接著,如果個位數字一樣的話,他會將這些數字,由大至小排
26 46 51 的話,
排好之後是:51 46 26
泡沫排序(Bubble Sort)
程式碼
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,a[1001];
while(cin>>n){
for(int i=0;i<n;i++){
cin>>a[i];
}
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
if((a[j]%10>a[j+1]%10)||(a[j]%10==a[j+1]%10&&a[j]<a[j+1])){
swap(a[j],a[j+1]);
}
}
}
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
}泡沫排序(Bubble Sort)

話又說回來
結果我們的小泡沫還是不太蒸氣
執行程式要花的時間太長
所以花心的人類又去另尋新歡了
選擇排序(Selection Sort)
選擇數列中的最小(或最大)元素,將其放在已排序部分的末尾,然後繼續選擇下一個最小(或最大)元素,逐漸擴展已排序的部分。
為不穩定排序法。
選擇排序(Selection Sort)
(1)找最小值:
從「未排序好的數字」中找到最小值
(2)丟到左邊:
把最小值丟到「未排序好的數字」的最左邊,把它標示成已排序好
對,然後你就會水靈靈的發現,
這傢伙只需要兩個步驟而已
選擇排序(Selection Sort)
1
2
3
4
5
1
2
3
4
5
選擇排序(Selection Sort)
1
2
3
4
5
選擇排序(Selection Sort)
1
2
3
4
5
選擇排序(Selection Sort)
1
2
3
4
5
選擇排序(Selection Sort)
1
2
3
4
5
選擇排序(Selection Sort)
1
2
3
4
5
選擇排序(Selection Sort)
程式碼(swap版本)
#include <bits/stdc++.h>
using namespace std;
int main(){
int a[5]={4,5,2,1,3};
int n=5;
for(int i=0;i<n;i++){
int min_index=i;//紀錄初始位置
for(int j=i+1;j<n;j++){ //不用管已經找完的左邊
if(a[j]<a[min_index])
min_index=j;//尋找最小值
}
swap(a[i],a[min_index]);
}
for(int i=0; i<n; i++){
cout<<a[i]<<' ';
}
}選擇排序(Selection Sort)
選擇排序(Selection Sort)

插入排序(Insertion sort)
將資料列假設分成已排序和未排序的兩部分,每次從未排序的資料中,挑選出一個元素,插入到已排序的資料中,直到所有的資料都已排序完成。
為穩定排序法。
插入排序(Insertion sort)
使用時機:
(1) 當元素數量較少時
(2) 當陣列裡的元素幾乎已排序,在整個大數量的陣列中只有少數元素放錯了位置時

插入排序(Insertion sort)
步驟:
(1) 從資料列的第二個元素開始,逐一取出每個目標元素
(2) 將目標元素與已排序的資料列中的元素逐一比較,直到找到一個比目標元素大的元素或搜尋完所有已排序的資料列。
(3) 將目標元素插入到適當的位置。
(4) 重複直到所有元素都已排序完成。
插入排序(Insertion sort)
每次考慮前n個元素,將第n個元素插入到指定的位置,讓第1個到第n個元素由小到大排序好,重複直到排序完成。
這東西看起來有點難以理解的話,
讓我們整理一下:
1
2
3
4
5
插入排序(Insertion sort)
1
2
3
4
5
插入排序(Insertion sort)
1
2
3
4
5
插入排序(Insertion sort)
1
2
3
4
5
插入排序(Insertion sort)
1
2
3
4
5
插入排序(Insertion sort)
是不是感覺這個過程有點熟悉?
尤其過年的時候特別常見對吧?
插入排序(Insertion sort)


好吧可能動漫角色耍帥的時候也很常用
嘿對,就是撲克牌
插入排序(Insertion sort)


我們在整理撲克牌的時候,就在跟插入排序say hello 了
插入排序(Insertion sort)
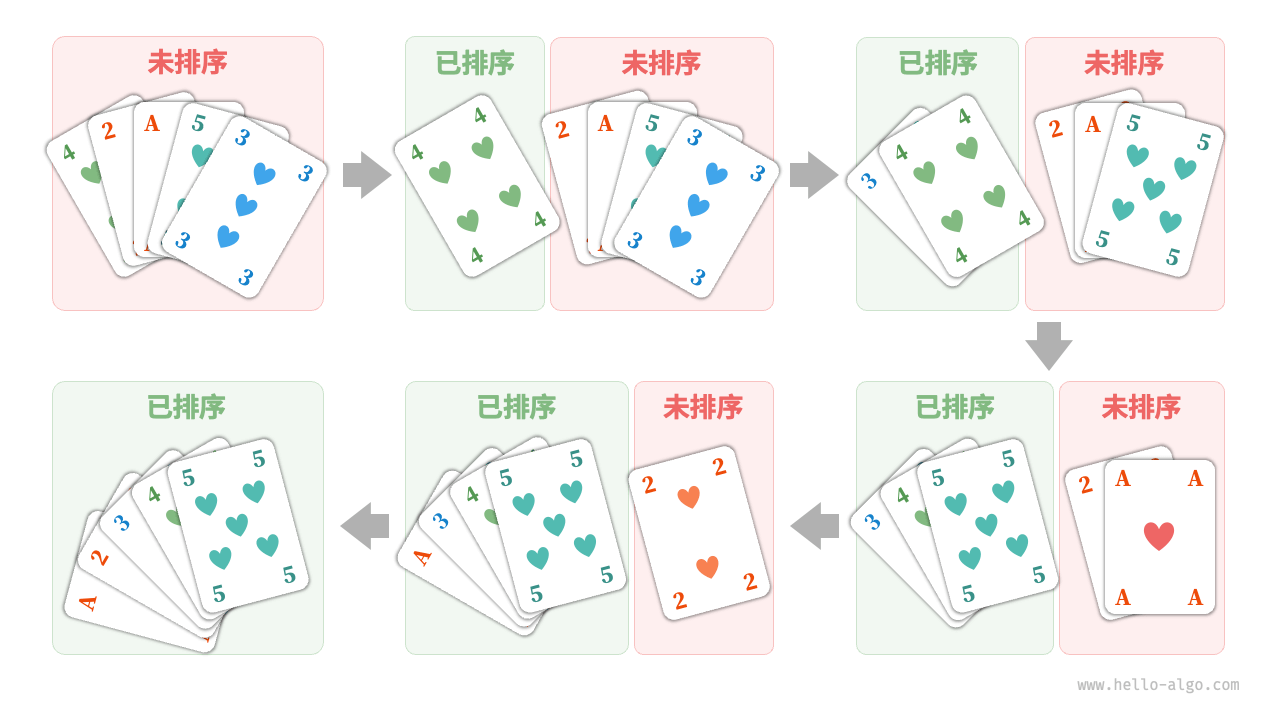

程式碼(while版本)
#include <bits/stdc++.h>
using namespace std;
int main(){
int a[5] = {3,2,5,1,4};
int n=5;
for(int i=1;i<n;i++){//第二個元素開始比較
int insert_num=a[i];
int j=i-1; //往左比大小(已排序資料)
while(j>=0&&a[j]>insert_num){
swap(a[j+1],a[j]);
j--;
}
}
for(int i=0;i<n;i++){
cout<<a[i]<<' ';
}
}插入排序(Insertion sort)
程式碼(for版本)
#include <iostream>
using namespace std;
int main() {
int a[5]={3,2,5,1,4},insert;
for(int i=1;i<5;i++){
insert=a[i];
for(int j=i-1;j>=0;j--){
if(insert<a[j]){
swap(a[j+1],a[j]);
}
else break;
}
}
for(int i=0;i<5;i++){
cout << a[i] << " ";
}
}插入排序(Insertion sort)
插入排序(Insertion sort)
點進去是補充影片,有興趣可以看看
這才算一點點而已
畢業是不可能的
合併排序(Merge Sort)
MergeSort 是一種經典的分治排序演算法,其主要思想是將待排序的陣列分割成兩個子陣列,然後分別對這兩個子陣列進行排序,最後再將排好序的子陣列合併起來。
為穩定排序法。
-
分割(Divide)
-
排序(Sort)
-
合併(Merge)
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
分割程式碼
void MergeSort(int Array[], int front, int end) {
if (front < end) {
//重複直到每個分組只剩下一個值
int mid = front + (end - front) / 2; // 計算中間值
MergeSort(Array, front, mid);
MergeSort(Array, mid + 1, end);//遞迴對左右兩部分進行排序
Merge(Array, front, mid, end);//合併到原始陣列中
}
}
合併排序(Merge Sort)
讀取陣列程式碼
void Merge(int Array[], int front, int mid, int end) {
// 將陣列分成兩個子陣列,並複製到 LeftSubArray 和 RightSubArray
int n1 = mid - front + 1; // 計算左子陣列的大小
int n2 = end - mid; // 計算右子陣列的大小
int LeftSubArray[n1], RightSubArray[n2];
// 將元素複製到左子陣列
for (int i = 0; i < n1; i++)
LeftSubArray[i] = Array[front + i];
// 將元素複製到右子陣列
for (int j = 0; j < n2; j++)
RightSubArray[j] = Array[mid + 1 + j];
}合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
排序+合併程式碼
void Merge(int Array[], int front, int mid, int end) {
int i = 0, j = 0, k = front;
// 將左右子陣列中的元素進行比較,合併到原始陣列中
while (i < n1 && j < n2) {
if (LeftSubArray[i] <= RightSubArray[j]) {
Array[k] = LeftSubArray[i];
i++;
}
else {
Array[k] = RightSubArray[j];
j++;
}
k++;
}
}合併排序(Merge Sort)
最終判斷程式碼
void Merge(int Array[], int front, int mid, int end) {
// 將左子陣列中剩餘的元素放入原始陣列
while (i < n1) {
Array[k] = LeftSubArray[i];
i++;
k++;
}
// 將右子陣列中剩餘的元素放入原始陣列
while (j < n2) {
Array[k] = RightSubArray[j];
j++;
k++;
}
}合併排序(Merge Sort)
1
2
3
4
5
6
合併排序(Merge Sort)
遞迴法程式碼(理解用版本)
#include <bits/stdc++.h>
using namespace std;
void Merge(int Array[], int front, int mid, int end) {
// 將陣列分成兩個子陣列,並複製到 LeftSubArray 和 RightSubArray
int n1 = mid - front + 1; // 計算左子陣列的大小
int n2 = end - mid; // 計算右子陣列的大小
int LeftSubArray[n1], RightSubArray[n2];
// 將元素複製到左子陣列
for (int i = 0; i < n1; i++)
LeftSubArray[i] = Array[front + i];
// 將元素複製到右子陣列
for (int j = 0; j < n2; j++)
RightSubArray[j] = Array[mid + 1 + j];
int i = 0, j = 0, k = front;
// 將左右子陣列中的元素進行比較,合併到原始陣列中
while (i < n1 && j < n2) {
if (LeftSubArray[i] <= RightSubArray[j]) {
Array[k] = LeftSubArray[i];
i++;
} else {
Array[k] = RightSubArray[j];
j++;
}
k++;
}
// 將左子陣列中剩餘的元素放入原始陣列
while (i < n1) {
Array[k] = LeftSubArray[i];
i++;
k++;
}
// 將右子陣列中剩餘的元素放入原始陣列
while (j < n2) {
Array[k] = RightSubArray[j];
j++;
k++;
}
}
void MergeSort(int Array[], int front, int end) {
if (front < end) {
// 計算中間索引,並遞迴地對左右兩部分進行排序和合併
int mid = front + (end - front) / 2;
MergeSort(Array, front, mid);
MergeSort(Array, mid + 1, end);
Merge(Array, front, mid, end);
}
}
合併排序(Merge Sort)
遞迴法程式碼(可輸入輸出版本)
#include <iostream>
using namespace std;
// 合併兩個已排序的子陣列
void Merge(int Array[], int front, int mid, int end) {
// 計算左右子陣列的大小
int n1 = mid - front + 1;
int n2 = end - mid;
// 創建左右子陣列
int LeftSubArray[n1], RightSubArray[n2];
// 複製元素到左子陣列
for (int i = 0; i < n1; i++)
LeftSubArray[i] = Array[front + i];
// 複製元素到右子陣列
for (int j = 0; j < n2; j++)
RightSubArray[j] = Array[mid + 1 + j];
int i = 0, j = 0, k = front;
// 合併左右子陣列到原始陣列中
while (i < n1 && j < n2) {
if (LeftSubArray[i] <= RightSubArray[j]) {
Array[k] = LeftSubArray[i];
i++;
}
else {
Array[k] = RightSubArray[j];
j++;
}
k++;
}
// 將左子陣列中剩餘的元素放入原始陣列
while (i < n1) {
Array[k] = LeftSubArray[i];
i++;
k++;
}
// 將右子陣列中剩餘的元素放入原始陣列
while (j < n2) {
Array[k] = RightSubArray[j];
j++;
k++;
}
}
// 遞迴排序
void MergeSort(int Array[], int front, int end) {
if (front < end) {
// 計算中間索引,並遞迴地對左右兩部分進行排序和合併
int mid = front + (end - front) / 2;
MergeSort(Array, front, mid);
MergeSort(Array, mid + 1, end);
Merge(Array, front, mid, end);
}
}
int main() {
int Array[6];
cout << "Enter 6 elements: ";
for (int i = 0; i < 6; ++i)
cin >> Array[i];
MergeSort(Array, 0, 5);
cout << "Sorted array: ";
for (int i = 0; i < 6; ++i)
cout << Array[i] << " ";
cout << endl;
return 0;
}
#include <bits/stdc++.h>
using namespace std;
// 合併兩個已排序的子陣列
void Merge(int Array[], int front, int mid, int end) {
// 計算左右子陣列的大小
int n1 = mid - front + 1;
int n2 = end - mid;
// 創建左右子陣列
int LeftSubArray[n1], RightSubArray[n2];
// 複製元素到左子陣列
for (int i = 0; i < n1; i++)
LeftSubArray[i] = Array[front + i];
// 複製元素到右子陣列
for (int j = 0; j < n2; j++)
RightSubArray[j] = Array[mid + 1 + j];
int i = 0, j = 0, k = front;
// 合併左右子陣列到原始陣列中
while (i < n1 && j < n2) {
if (LeftSubArray[i] <= RightSubArray[j]) {
Array[k] = LeftSubArray[i];
i++;
}
else {
Array[k] = RightSubArray[j];
j++;
}
k++;
}
// 將左子陣列中剩餘的元素放入原始陣列
while (i < n1) {
Array[k] = LeftSubArray[i];
i++;
k++;
}
// 將右子陣列中剩餘的元素放入原始陣列
while (j < n2) {
Array[k] = RightSubArray[j];
j++;
k++;
}
}
// 遞迴排序
void MergeSort(int Array[], int front, int end) {
if (front < end) {
// 計算中間索引,並遞迴地對左右兩部分進行排序和合併
int mid = front + (end - front) / 2;
MergeSort(Array, front, mid);
MergeSort(Array, mid + 1, end);
Merge(Array, front, mid, end);
}
}
int main() {
int Array[6];
cout << "Enter 6 elements: ";
for (int i = 0; i < 6; ++i)
cin >> Array[i];
MergeSort(Array, 0, 5);
cout << "Sorted array: ";
for (int i = 0; i < 6; ++i)
cout << Array[i] << " ";
cout << endl;
return 0;
}
合併排序(Merge Sort)


快速排序(Quick Sort)
常見的分治演算法,被認為是最快的排序演算法之一。
選擇一個基準元素,將待排序列分為兩部分,其中一部分的所有元素都比基準元素小,另一部分的所有元素都比基準元素大,然後再按照此方法對這兩部分進行快速排序,直到序列有序。
為不穩定排序法。
快速排序(Quick Sort)
快速排序演算法是透過分治,達成高效率的排序演算法。它可以在短時間內對大型數據進行排序。
快速排序(Quick Sort)
Quick Sort 與 Merge Sort 雖然利用同樣的概念,但是作法上差異很大,它會先從陣列中選擇一個「樞紐」(pivot),然後將所有小於樞紐的值都移到它的左邊、將所有大於樞紐的值都移到它的右邊。移動的過程我們並沒有去做排序,我們只是先將它們移到某一邊。
結束時,只有 pivot 會在它最後正確的位置上
當樞紐完成以後,我們對左半部分再次進行同樣的處理(找到 pivot、移動位置),再處理右半部分。
快速排序(Quick Sort)
先來看看第一種,遞迴版本
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
pivot
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
>4
<4
1
2
3
4
5
快速排序(Quick Sort)
>4
<4
1
2
3
4
5
快速排序(Quick Sort)
>4
<4
1
2
3
4
5
快速排序(Quick Sort)
>4
<4
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
快速排序(Quick Sort)
先看左半邊
1
2
3
4
快速排序(Quick Sort)
pivot
1
2
3
4
快速排序(Quick Sort)
1
2
3
4
快速排序(Quick Sort)
1
2
3
4
快速排序(Quick Sort)
pivot
1
2
3
4
快速排序(Quick Sort)
繼續看左半邊
1
2
3
4
快速排序(Quick Sort)
pivot
左邊的元素為0或1時,停止執行
1
2
3
4
快速排序(Quick Sort)
pivot
左邊的元素為0或1時,停止執行
1
2
3
4
快速排序(Quick Sort)
5
排序完畢
尚未排序
所以再來看右邊
4
快速排序(Quick Sort)
5
pivot
左邊的元素為0或1時,停止執行
為什麼是看左邊?
因為我們不管4
只看兩邊資料列
4
快速排序(Quick Sort)
5
合併
1
2
3
程式碼(遞迴版)
#include <iostream>
using namespace std;
// 快速排序函式
void QuickSort(int arr[],int n,int result[],int& index) {
if (n <= 0) {
return; // 若陣列長度小於等於 0,直接返回
}
int pivot=arr[0]; //以第一個元素作為pivot
int leftCount=0, rightCount=0;
int left[n],right[n]; // 暫存左邊和右邊的元素
for(int i=1;i<n;i++) { // 將陣列元素分配到左邊或右邊
if(arr[i]<pivot){
left[leftCount++]=arr[i];
}
else{
right[rightCount++]=arr[i];
}
}
// 遞迴排序左邊的陣列
QuickSort(left,leftCount,result,index);
// 插入pivot到結果陣列
result[index++]=pivot;
// 遞迴排序右邊的陣列
QuickSort(right,rightCount,result,index);
}
int main(){
int data[]={4,3,5,1,2};
int n=sizeof(data)/sizeof(data[0]); //計算陣列長度
int result[n]; //儲存排序結果
int index=0; //結果陣列的索引
cout<<"Before sorting:";
for(int i=0;i<n;i++){
cout<<data[i]<<" ";
}
cout<<endl;
QuickSort(data,n,result,index);
cout<<"After sorting:";
for(int i=0;i<n;i++){
cout<<result[i]<<" ";
}
cout<<endl;
return 0;
}
快速排序(Quick Sort)
前面的版本會需要額外的記憶體空間(遞迴部分),
第二個版本不需要額外的子數列記憶體空間,
因為只會更改原本的數列,切割的同時也就等同合併了,
所以只需花費一點點空間。
實作時會需要用到輔助函式,來直接分割原本的數列。
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
pivot
1
2
3
4
5
快速排序(Quick Sort)
pivot
L:記錄下一個<pivot的元素要交換到的位置
i索引:尋找<pivot的值
L
i
1
2
3
4
5
快速排序(Quick Sort)
如果i<pivot,就交換
L
i
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
L
i
如果i>pivot,就跳過
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
L
若L右邊已經沒有元素或是其元素皆>pivot
交換pivot跟L的位置
1
2
3
4
5
快速排序(Quick Sort)
L
先看左邊
i
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
L
再來看右邊
1
2
3
4
5
快速排序(Quick Sort)
L
i
1
2
3
4
5
快速排序(Quick Sort)
1
2
3
4
5
快速排序(Quick Sort)
程式碼(in-place)
#include <iostream>
#include <array>
using namespace std;
// 分區函式:重新排列陣列並返回基準點的索引
int partition(array<int, 9>& arr, int start, int end) {
int pivot = arr[end]; // 將最後一個元素作為 pivot
int nextIndex = start; // 下一個小於 pivot 的位置
for (int i = start; i < end; i++) { // 遍歷 start 到 end-1
if (arr[i] < pivot) { // 若當前元素小於 pivot
swap(arr[nextIndex], arr[i]); // 交換位置
nextIndex++; // 更新下一個插入位置
}
}
swap(arr[nextIndex], arr[end]); // 將 pivot 放到正確位置
return nextIndex; // 返回 pivot 的索引
}
// 快速排序函式
void QuickSort(array<int, 9>& arr, int start, int end) {
if (start < end) { // 若子陣列長度大於 1
int pivotIndex = partition(arr, start, end); // 分區並獲取基準點索引
QuickSort(arr, start, pivotIndex - 1); // 遞迴排序左子陣列
QuickSort(arr, pivotIndex + 1, end); // 遞迴排序右子陣列
}
}
int main() {
array<int, 9> data = {50, 90, 70, 20, 10, 30, 40, 60, 80}; // 原始資料
QuickSort(data, 0, data.size() - 1); // 呼叫快速排序
// 輸出排序結果
for (int num : data) {
cout << num << " ";
}
cout << endl;
return 0;
}
快速排序(Quick Sort)
第三種
將原始資料列使用兩個指標,從資料列的兩端開始相互移動,直到它們相遇或反轉為止
快速排序(Quick Sort)
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
L找>pivot的值
R找<pivot的值
1
2
3
4
5
6
pivot
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
L直到找到>Pivot停下來
R直到找到<Pivot停下來
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
- L與R的資料互相交換,L與R繼續移動
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
- L與R反轉或重疊時,Pivot需進行交換
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
- L與R反轉時,R位置的資料與Pivot互相交換
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
L
R
- L與R重疊,重疊位置的資料Pivot互相交換
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
pivot
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
快速排序(Quick Sort)
1
2
3
4
5
6
排序程式碼
\#include <iostream>
#include <vector>
using namespace std;
// Partition 函數:將數列分割並返回基準元素的最終位置
int Partition(vector<int>& arr, int start, int end) {
int pivot = arr[start]; // 基準元素選擇數列的第一個元素
int leftPointer = start + 1; // 左指標從基準元素右邊的元素開始
int rightPointer = end; // 右指標從數列的最右邊開始
bool done = false; // 標誌,表示分割完成
while (!done) {
// 移動左指標,直到找到一個比基準大的元素
while (leftPointer <= rightPointer && arr[leftPointer] <= pivot) {
leftPointer++;
}
// 移動右指標,直到找到一個比基準小的元素
while (arr[rightPointer] >= pivot && rightPointer >= leftPointer) {
rightPointer--;
}
// 如果左右指標交錯,則分割完成
if (rightPointer < leftPointer) {
done = true;
} else {
// 否則交換左右指標指向的元素
swap(arr[leftPointer], arr[rightPointer]);
}
}
// 把基準元素交換到正確位置
swap(arr[start], arr[rightPointer]);
return rightPointer; // 返回基準元素的最終位置
}
// QuickSort 函數:遞歸排序
void QuickSort(vector<int>& arr, int start, int end) {
if (start < end) {
int pivotIndex = Partition(arr, start, end); // 找到基準元素的最終位置
QuickSort(arr, start, pivotIndex - 1); // 遞歸排序基準元素左邊的部分
QuickSort(arr, pivotIndex + 1, end); // 遞歸排序基準元素右邊的部分
}
}
int main() {
// 定義數列
vector<int> data = {4, 2, 5, 3, 6, 1};
// 呼叫 QuickSort 函數進行排序
QuickSort(data, 0, data.size() - 1);
// 輸出排序後的數列
for (int num : data) {
cout << num << " ";
}
cout << endl;
return 0;
}
快速排序(Quick Sort)
kahoot!
排序
By 愛錢成癡,嗜賭成癮
排序
- 210




