PROPIEDADES Y RECORRIDO DE ARBOLES 

Definición de arboles

Un árbol es un grafo no dirigido conexo que no contiene circuitos, es decir que no existen dos o más paseos sobre un par de vértices.

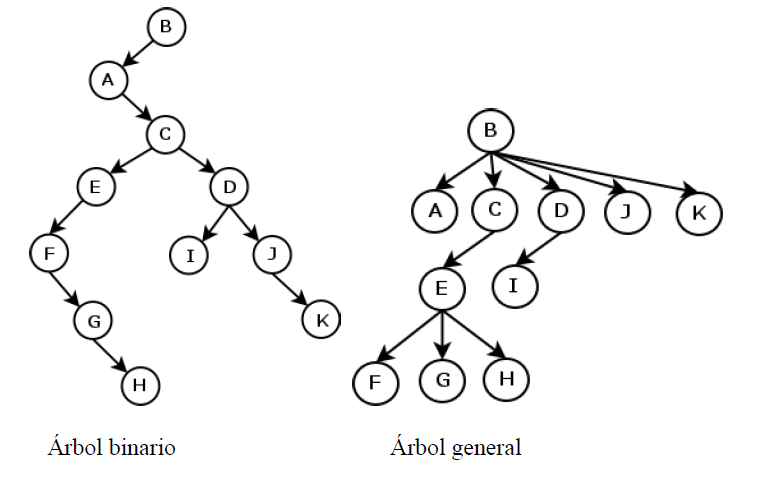
Un conjunto de árboles disjuntos es llamado bosque. Un vértice de grado 1 en un árbol se llama hoja o un nodo terminal, y un vértice de grado mayor que 1 recibe el nombre de rama o nodo interno.  Por ejemplo, son hojas:  b, c, d y los vértices a, A, B, C, D son nodos rama.

Las propiedades de los árboles son:

Existe un único paseo entre dos vértices cualesquiera de un árbol.  El número de vértices es mayor en uno al número de aristas de un árbol.  Un árbol con dos o más vértices tiene al menos dos hojas.

Un árbol T (libre) es una gráfica simple que satisface lo siguiente; si v y w son vértices en T, existe una trayectoria simple única de v a w. Se muestra un ejemplo:

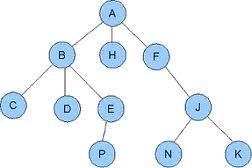
Un árbol con raíz es un árbol en el que un vértice específico se designa como raíz, se presenta un ejemplo:  

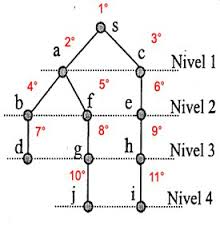
La altura de un árbol con raíz es el número máximo de nivel que ocurre.

Ejemplo:

Tomando como referencia el gráfico del árbol con raíz determine el nivel del vértice a, b, g y determine también la altura del árbol.

Para el vértice a su nivel es 0

Para el vértice b su nivel es 1

Para el vértice g su nivel es 2

La altura del árbol es de 2.

Arboles Binarios

Están entre los tipos de árboles binarios especiales con raíz, su característica es que todo vértice tiene cuando mucho dos hijos. Donde cada hijo se designa como un hijo izquierdo o un hijo derecho, además, su posición en el árbol los identifica.

Formalizando se dice que un árbol binario es un árbol con raíz en el que cada vértice tiene ningún hijo, un hijo o dos hijos.

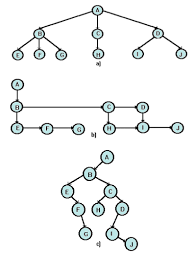
Si el vértice tiene un hijo se designa como un hijo izquierdo o como

derecho (pero no ambos). Si un vértice tiene dos hijos, un hijo se designa como hijo izquierdo y el otro como hijo derecho.

Un árbol binario completo es un árbol binario en el que cada vértice tiene dos o cero hijos.

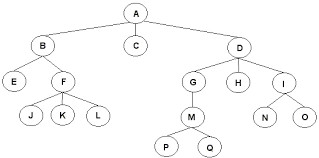
RECORRIDO DE ARBOLES

Para ello se necesita procedimientos que  permitan visitar cada vértice para acceder a los datos , los recorridos mas mas comunes son los siguientes:

* Recorido preorden 

*recorrido postorden

*recorrido inorden

* recorrido por nivel

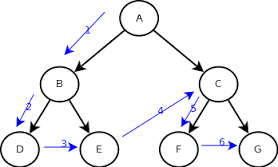
Recorrido pre orden

Sea T un un arbol ordenado con raiz r. si T consta solo de r, entonces r es el recorrido preorden de T. sino suponga que t1.t2.....tn son los subarboles en r listado de izquierda a derecha en T.

El recorrido en preorden inicia visitando r continua recorriendo t1, en preorden luego t2 en preorden y asi susesivamente hasta recorrer tn en preorden.

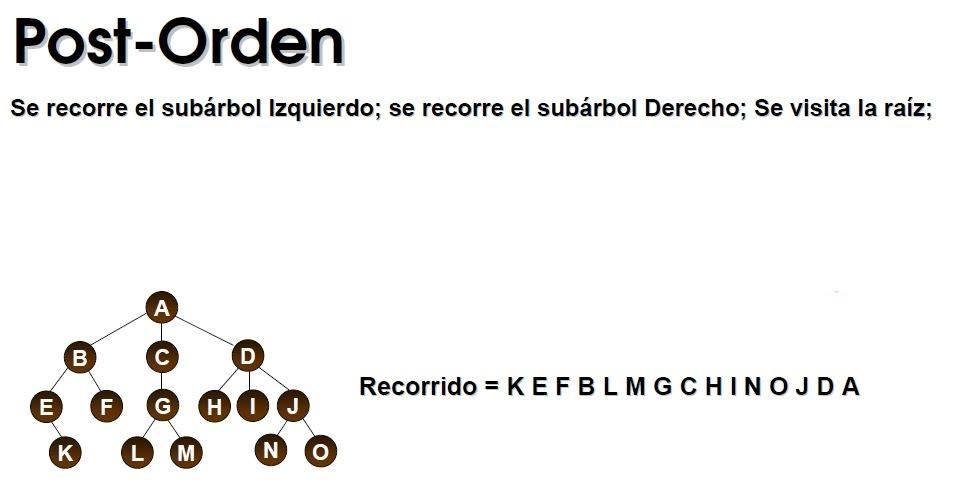
Recorrido postorden

Sea T un arbol ordenado con raiz r. si T consta solo de r, entonces r es el recorrido en postorden de T sino suponga que T1,T2......Tn son los subarboles en r listados de izquierda a derecha en t. 

El recorrido en postorden inicia recorriendo T1 en postorden luego recorre T2 en postorden, luego recorre Tn en postorden y así sucesivamente , finaliza visitando r de izquierda a derecha y de abajo hacia arriba.

Recorrido Inorden

SeaT un arbol ordenado con raiz r. si consta solo de r entonces r es el recorrido en inorden de T si no , suponga que T1,T2..TN son los subarboles en r listado de izquierda a derecha en T. el recorrido es inorden inicia recorriendo T1 en inorden y continua visitando r, a continuación recorre T2 en inorden ,luengo t3 en inorden y asi susesivamente hasta recorrer Tn en inorden de izquierda a derecha de abajo hacia arriba

Recorrido por nivel

Sea T un arbol ordenado con raiz R, siT solo consta de r, entonces r es el recorrido por nivel de T si no, si no suponga que T1, T2..TN son los subarboles en r listados de arriba hacia abajo

Gracias por su atención Dios los Bendiga