Simulation-based models for galaxy clustering
Carolina Cuesta-Lazaro
EAS 2022
Collaborators: Cheng-Zong Ruan, Yosuke Kobayashi, Enrique Paillas, Alexander Eggemeier, Pauline Zarrouk, Sownak Bose, Takahiro Nishimichi, Baojiu Li, Carlton Baugh
(\vec{\theta}_i, z_i)
\xi_\mathrm{data}(r)
\xi_\mathrm{model}(r|\mathcal{C})
\xi^S_\mathrm{data}(s_\perp, s_\parallel)
\xi^S_\mathrm{model}(s_\perp, s_\parallel|\mathcal{C})
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \blue{\xi^R(r)}\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
\blue{\xi^R(r)}
\xi^S(s_\perp, s_\parallel)
\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)
r
r_\parallel
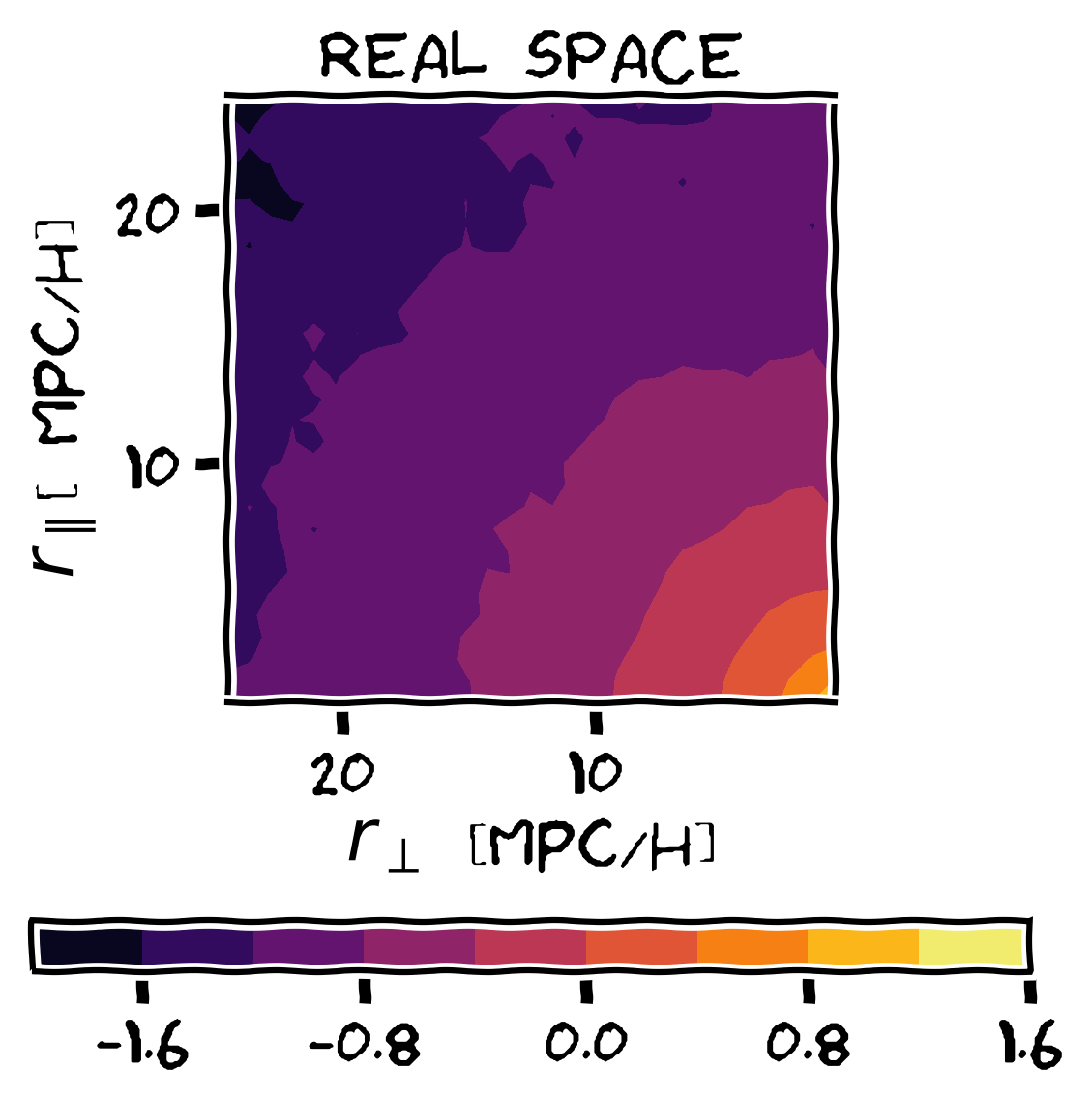
A halo model emulator
\langle v^i_{hh}(r|M_h)\rangle
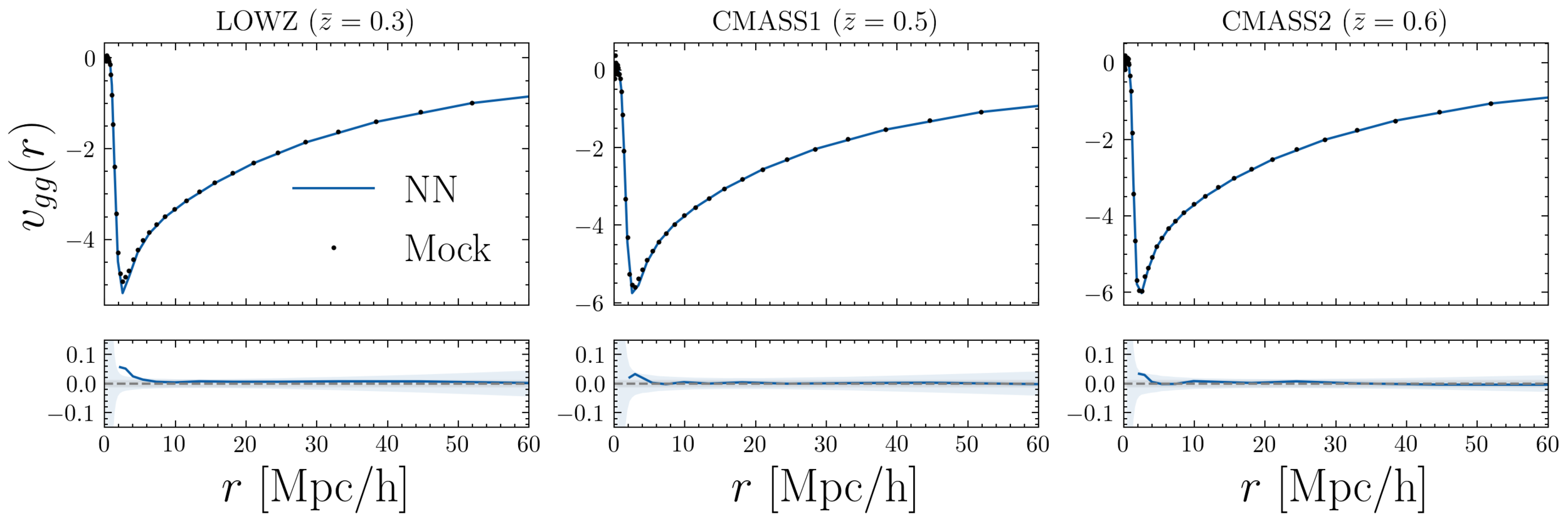
Neural Network Emulator
\xi^R_{hh}(r|M_h)
\{ \mathcal{C}, M_h, z \}
\{ \mathcal{G} \}
\xi^R_{gg}(r)
\langle v^i_{gg}(r)\rangle
\xi^S_{gg}(s_\perp, s_\parallel)
Fixing HOD
\log_{10} M (\delta^\mathrm{rank}_{2.5}) = \log_{10} M^0 + B_\mathrm{cen/sat} \times \left( \delta^\mathrm{rank}_{2.5} - 0.5 \right)
\bar{\xi}(R_s)
R_s
\bar{\xi}(R_s)
R_s
Density-dependent clustering
1
1
1
2
2
4
5
5
5
3
Conclusions
1. 100 N-body simulations are sufficient to emulate two point statistics to the accuracy of current surveys (future?)
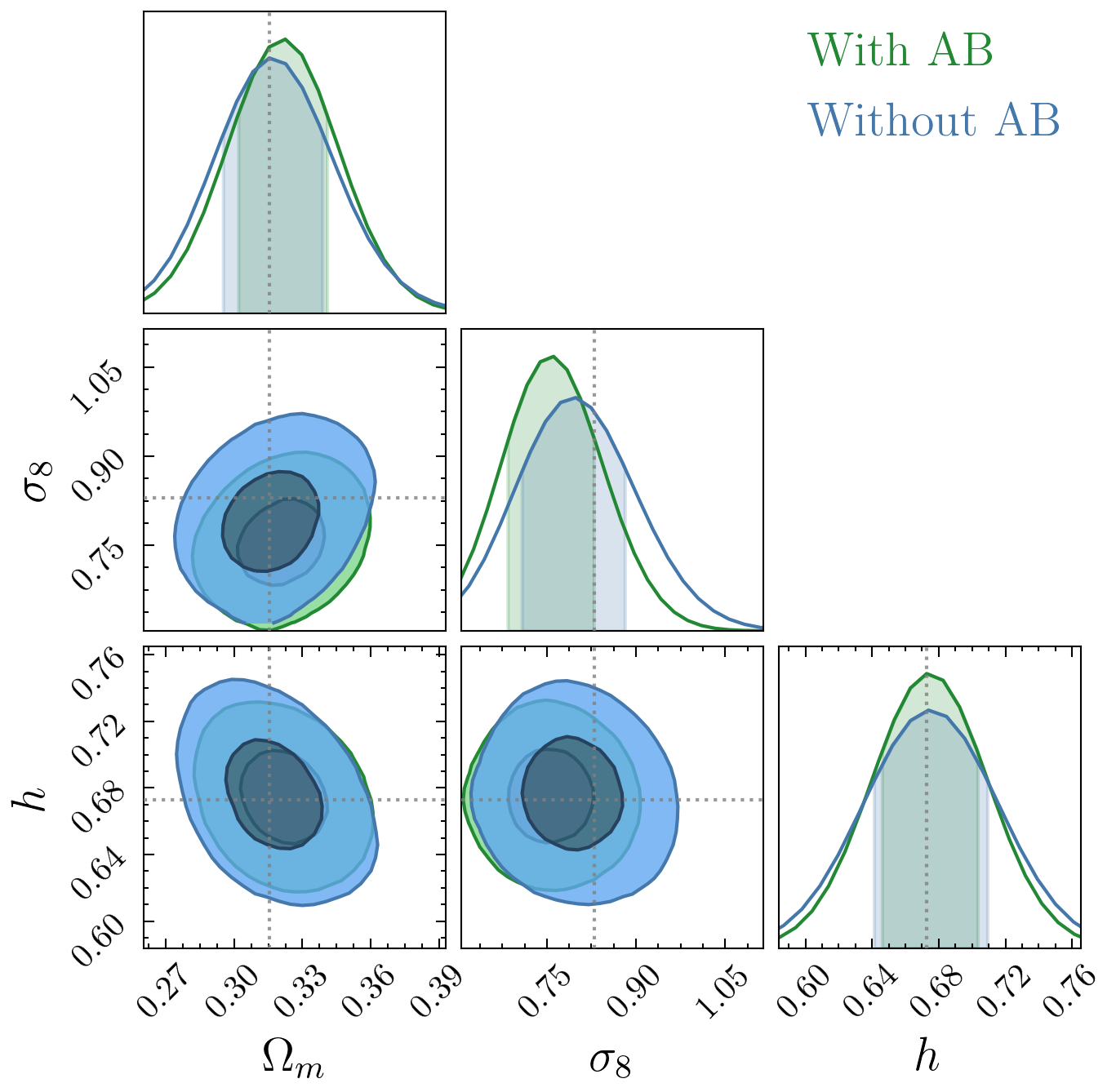
2. Ignoring environment assembly bias effects could bias constraints
\sigma_8
3. Cosmological constraints could be improved dramatically by modelling environment dependent clustering (specially to constrain sum of neutrino masses)
4. But, potentially new systematics?
1. Emulating 2-point statistics (clustering + velocity) with neural networks
2. Potential consequences of ignoring environment based assembly bias
3. Extracting non-Gaussian information from environment dependent clustering
Outlook
LOWZ MOCK
\mathcal{O}(100)
N-body sims DarkQuest
EAS22
By carol cuesta
