Enrique Paillas, Pauline Zarrouk, Yan-Chuan Cai, Will Percival, Sesh Nadathur, Mathilde Pinon, Arnaud de Mattia, Florian Beuler
Constraining vΛCDM:
beyond two-point functions
Carolina Cuesta-Lazaro
IAIFI fellow - MIT/CfA
arXiv:2209.04310
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}}
t = 380,000 \: \mathrm{years}
\delta = \red{F}(\delta_i)
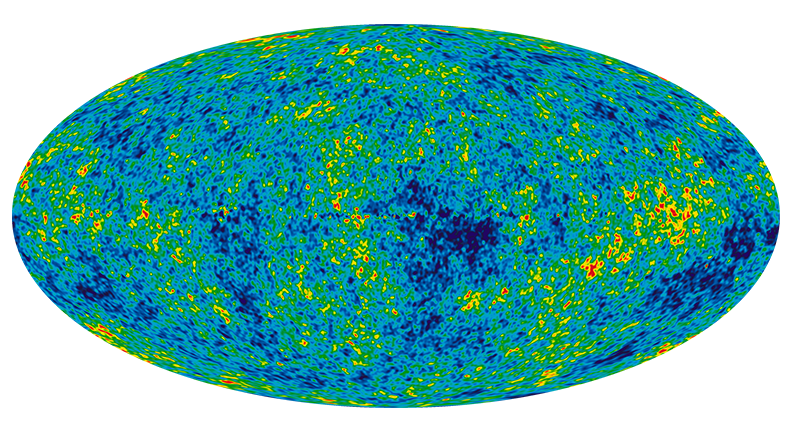
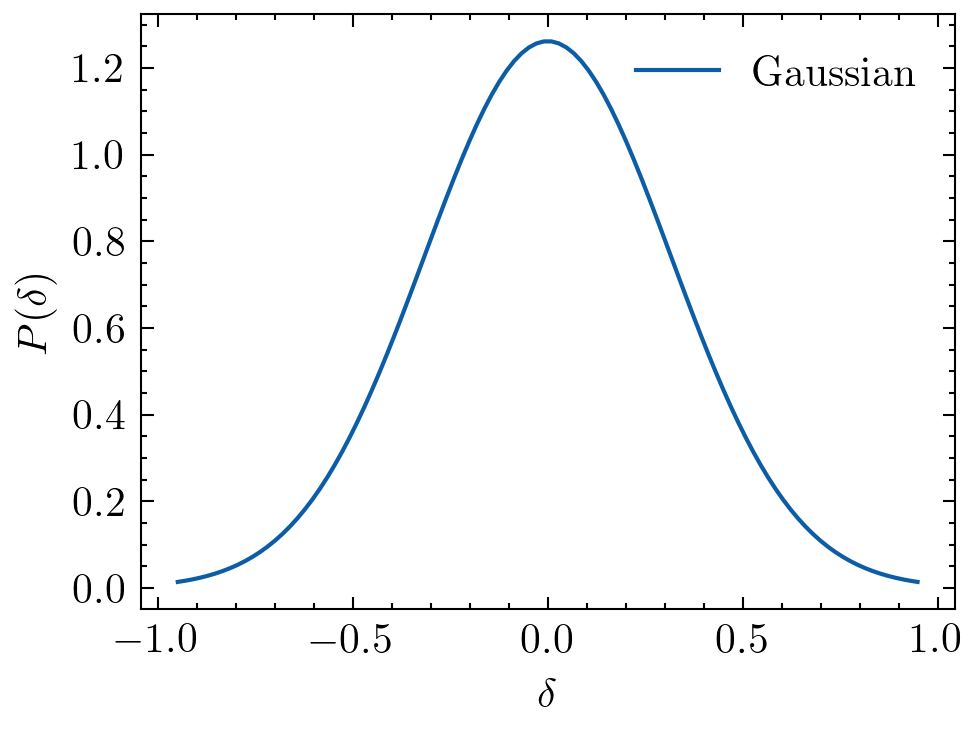
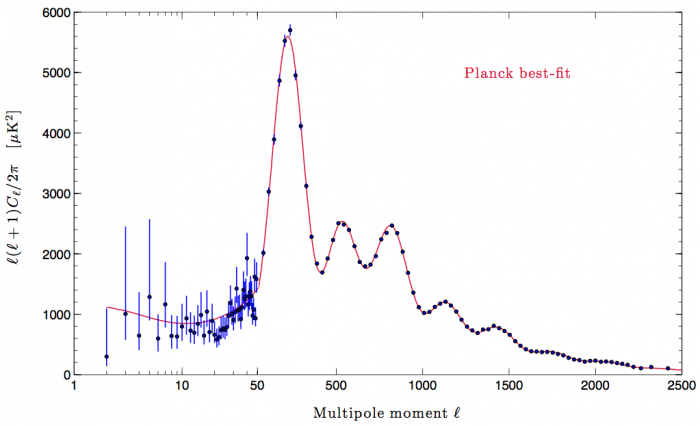
Linear
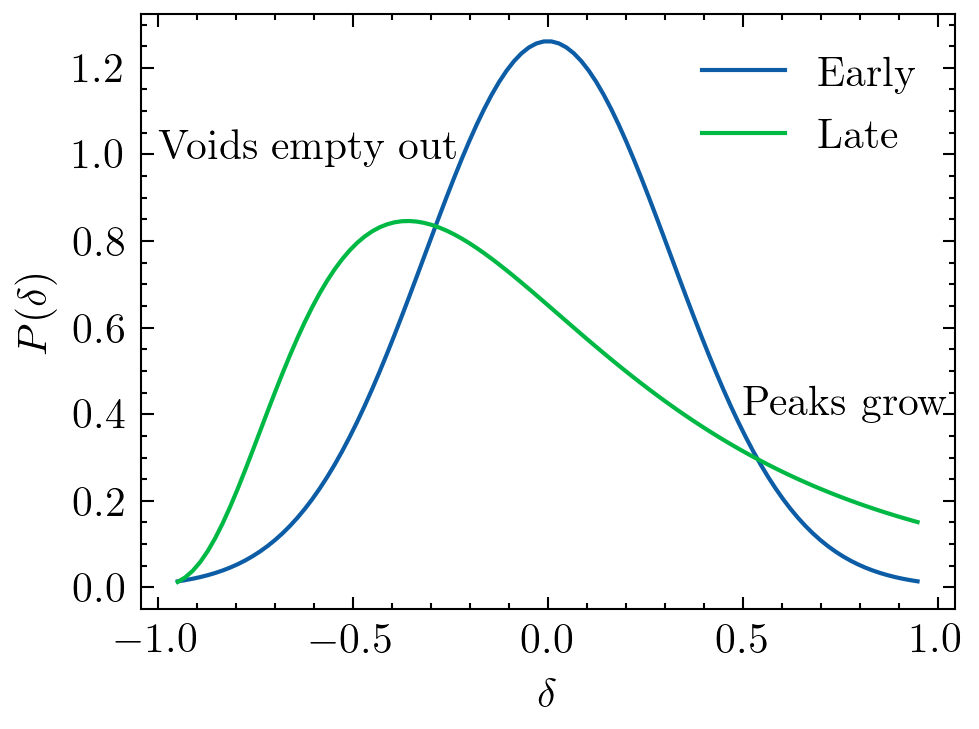
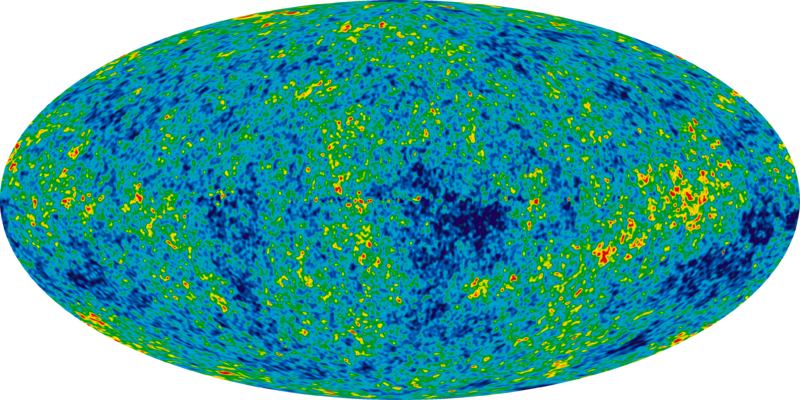
Early Universe
~linear
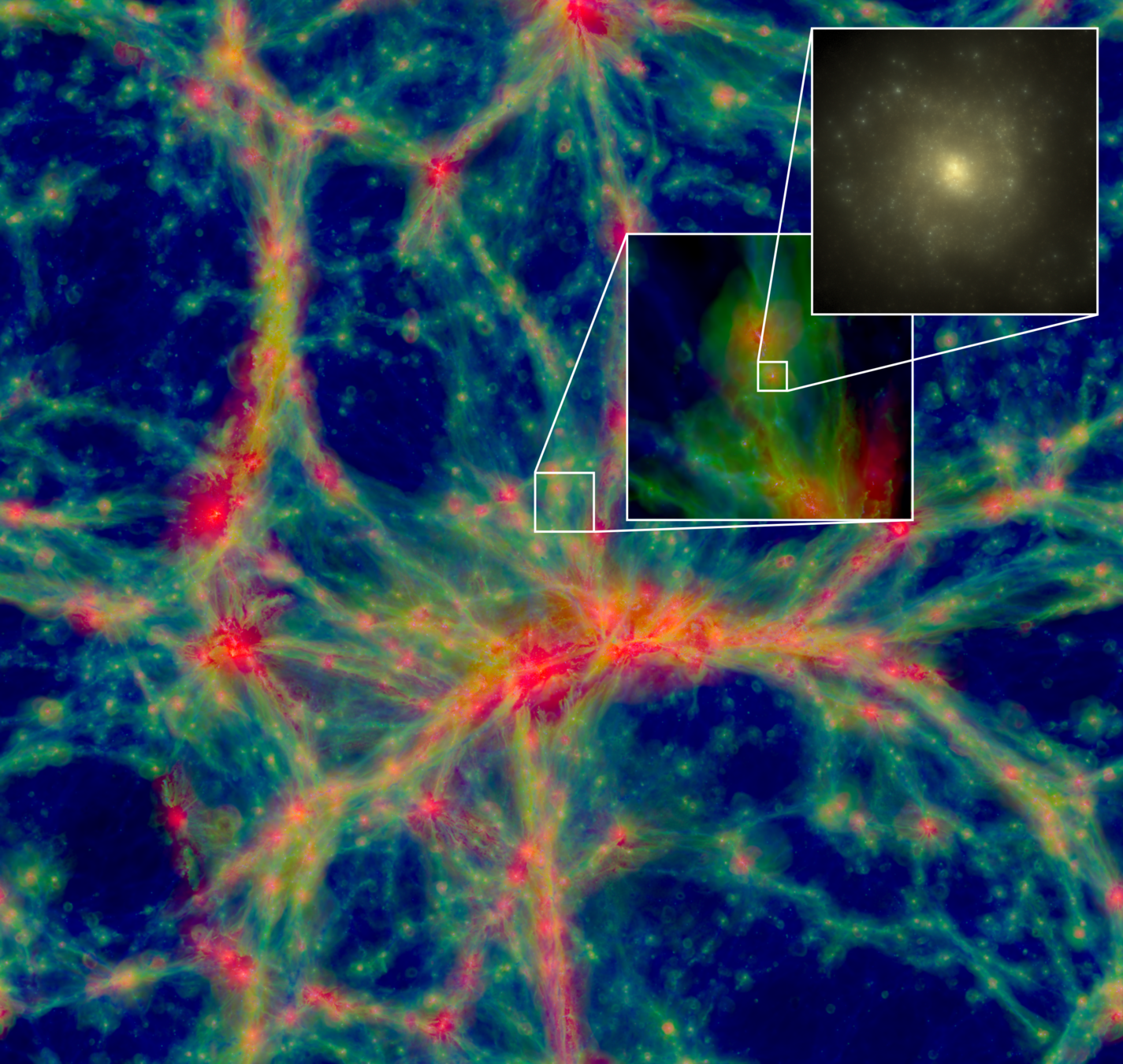
Gravity
Late Universe
Non-linear
Credit: S. Codis+16
Non-Guassianity
Second moment not optimal
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
\bar{\xi}(R_s)
R_s
1
1
1
2
2
4
5
5
5
3
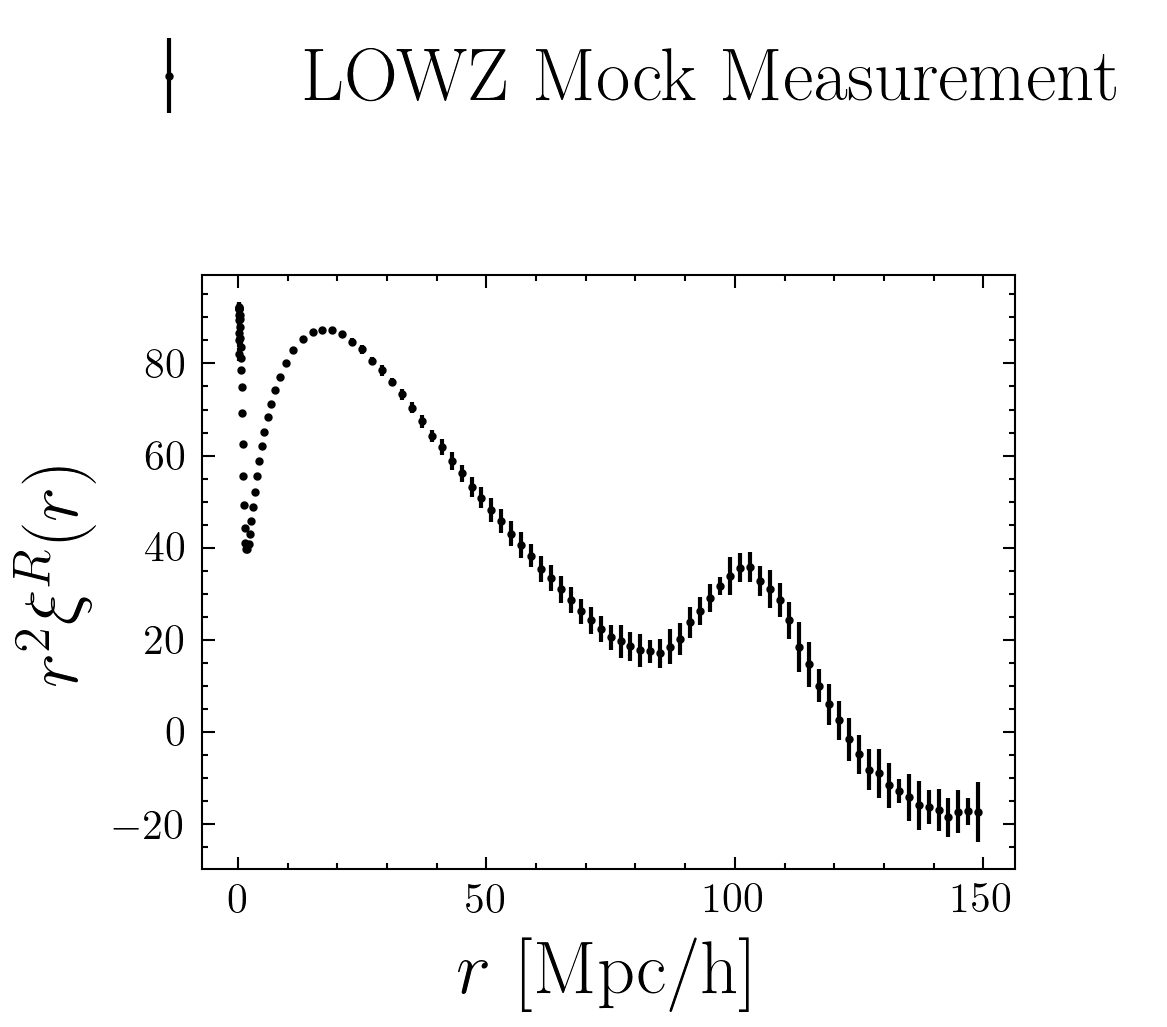
arxiv:1911.11158
1
1
1
2
2
4
5
5
5
3
Autocorrelation
10
50
90
130
Cross-correlation with haloes
Monopole
Quadrupole
Voids
Clusters
10
50
90
130
s^2
s^2
F_{\alpha \beta} = \mathbb{E} \left[\frac{\partial^2 \ln \mathcal{L}(x|\theta)}{\partial \theta_i \partial \theta_j} \right] = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
\delta \theta_\alpha \geq \left( F^{-1} \right)_{\alpha \alpha}
\frac{\partial \log \mathcal{L}(x|\theta)} {\partial \theta} = 0
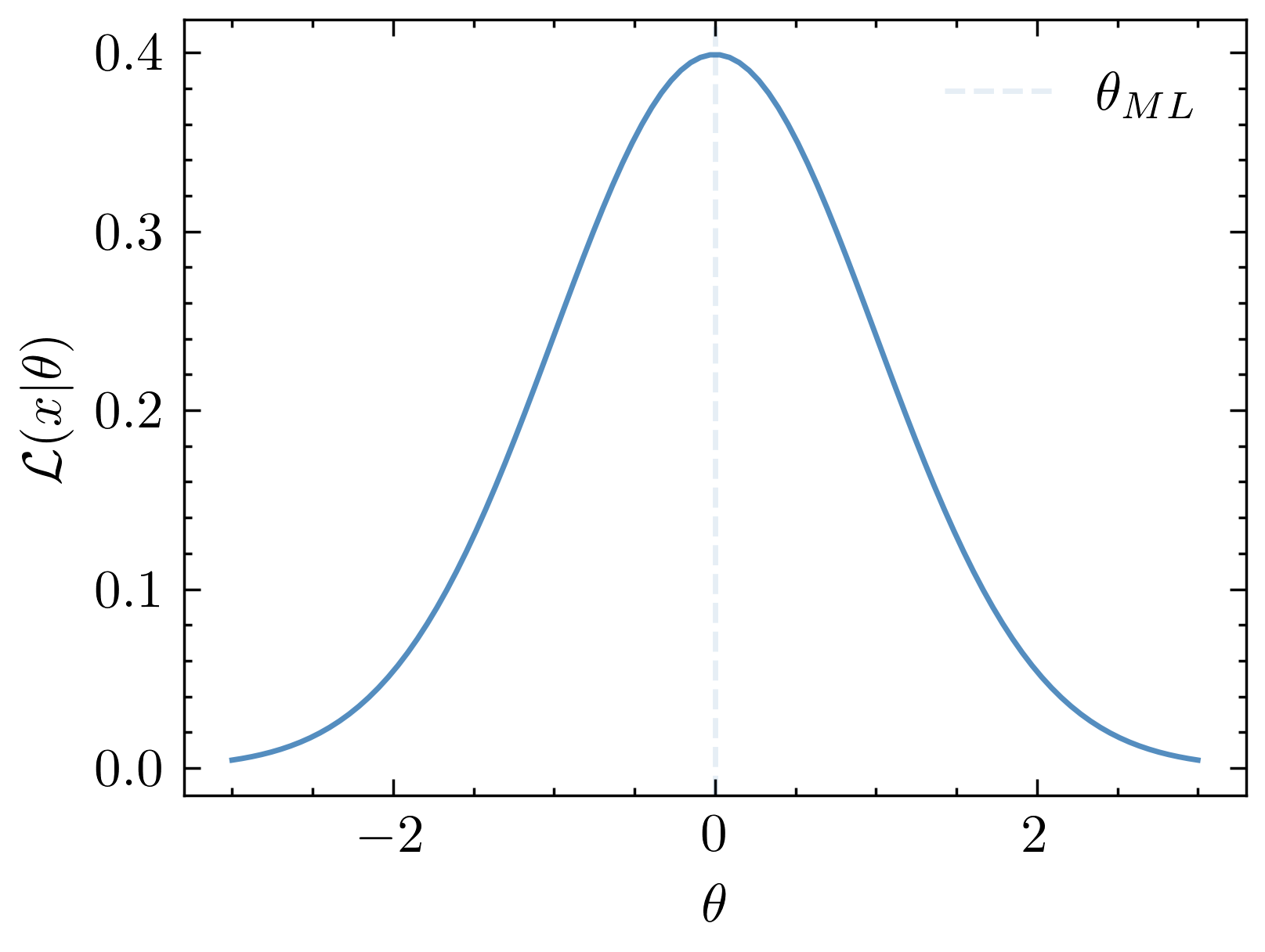
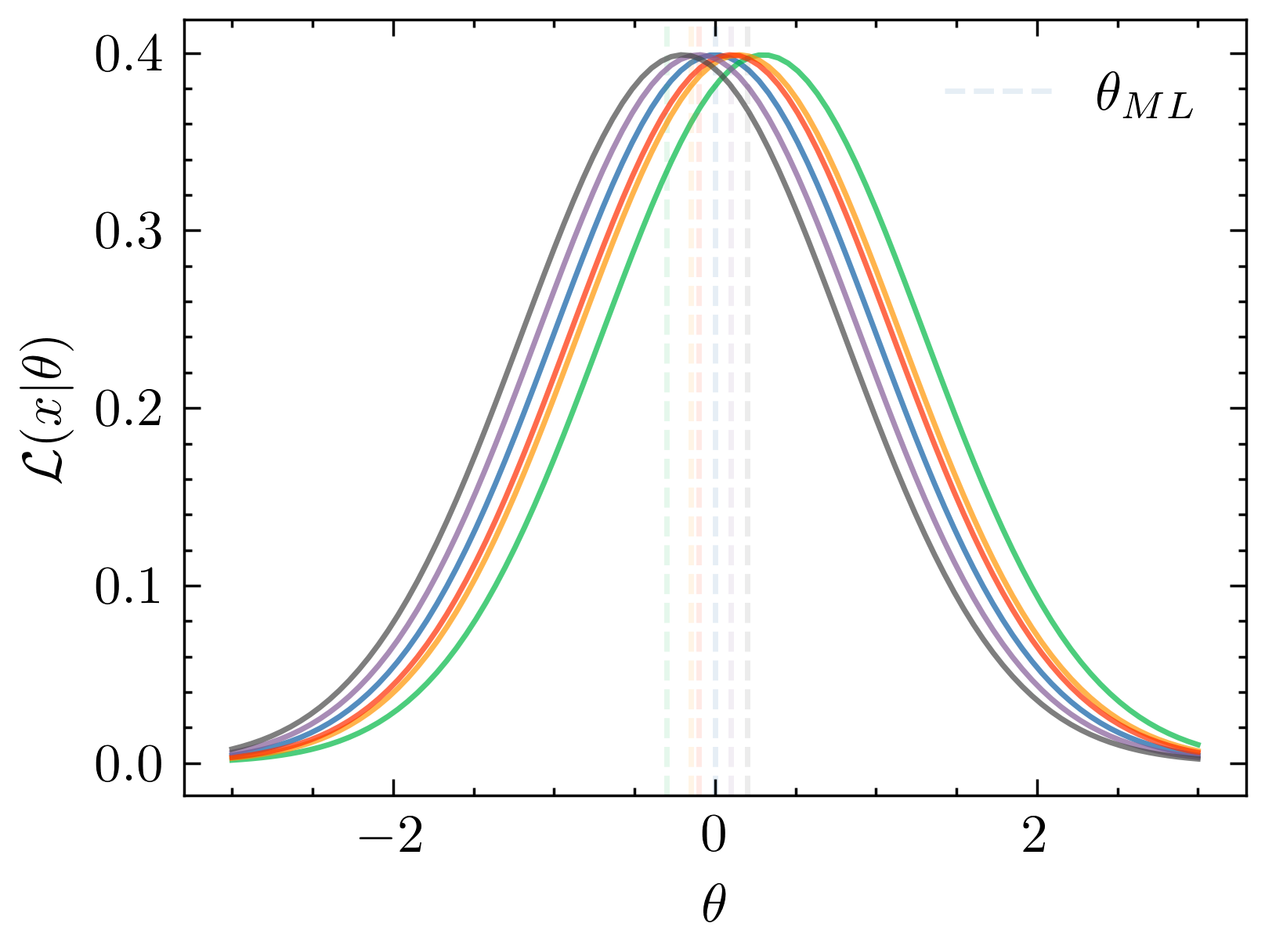
Estimating sensitivity to cosmology: Fisher information
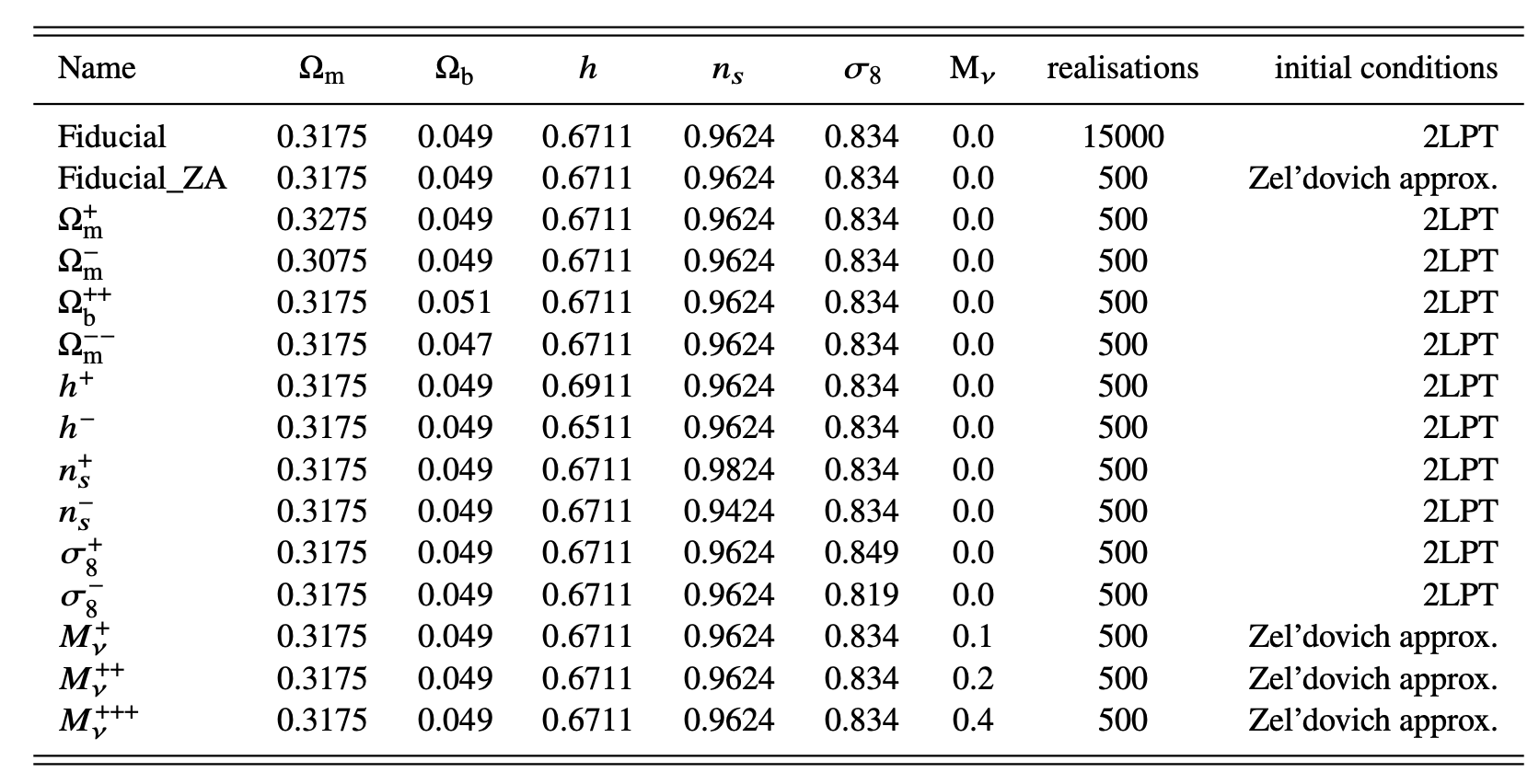
The Quijote simulations
arXiv:1909.05273
Covariance
Derivatives
\frac{\partial \bm{S}}{\partial \bm{\theta}} \simeq \frac{{\bm S}(\bm{\theta} + {\rm d}\bm{\theta}) - {\bm S}(\bm{\theta} - {\rm d}\bm{\theta})}{2 \rm{d}\bm{\theta}}
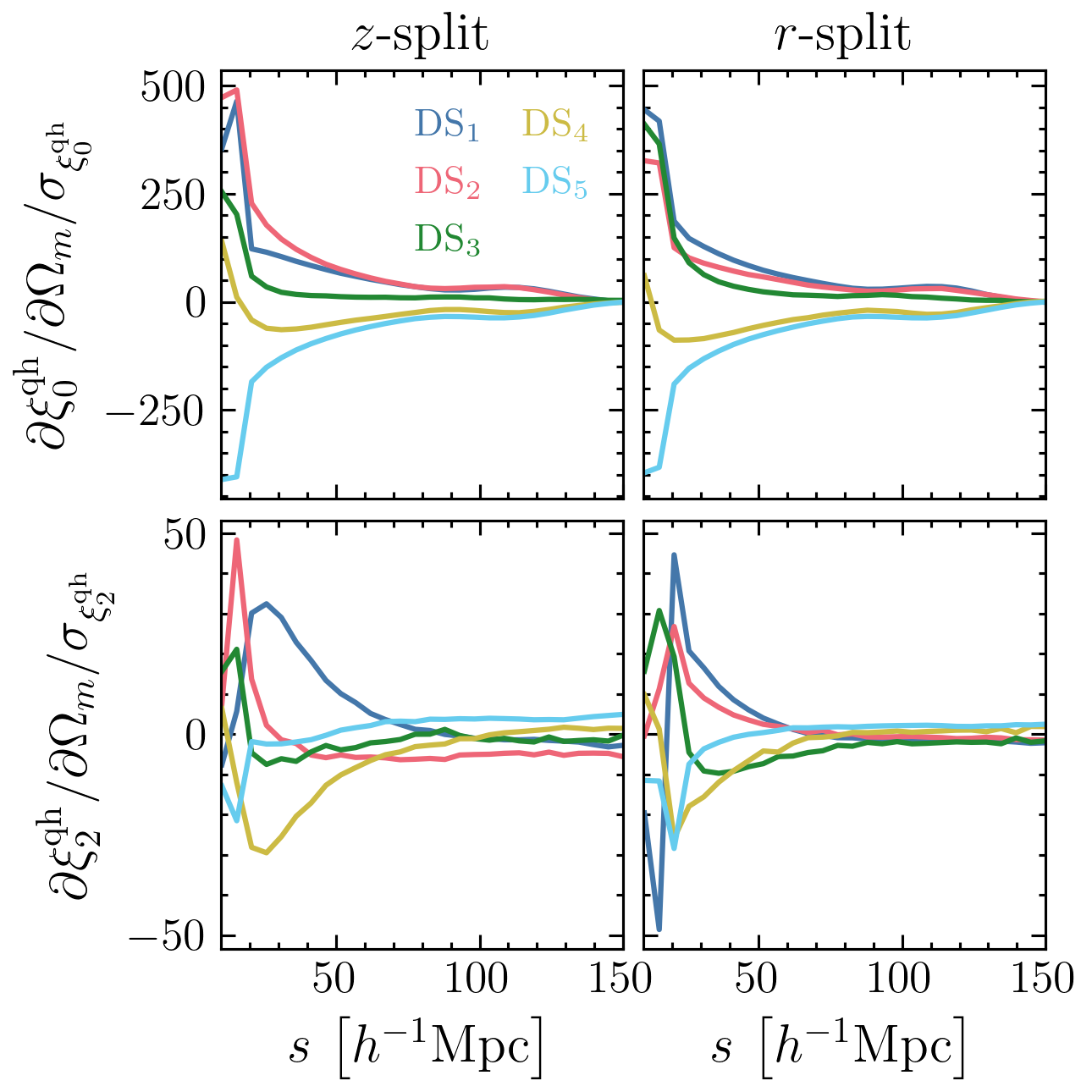
Finite differences
F_{\alpha \beta} = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
0
C = \frac{1}{n_{\rm sim} - 1} \sum_{k=1}^{n_{\rm sim}} \left({\bm{S}_{k}} - \overline{\bm{S}}\right)\left({\bm{S}_{k}} - \overline{\bm{S}}\right)
F_{\alpha \beta} = \frac{\partial S}{\partial \theta_\alpha} C^{-1} \frac{\partial S}{\partial \theta_\beta}
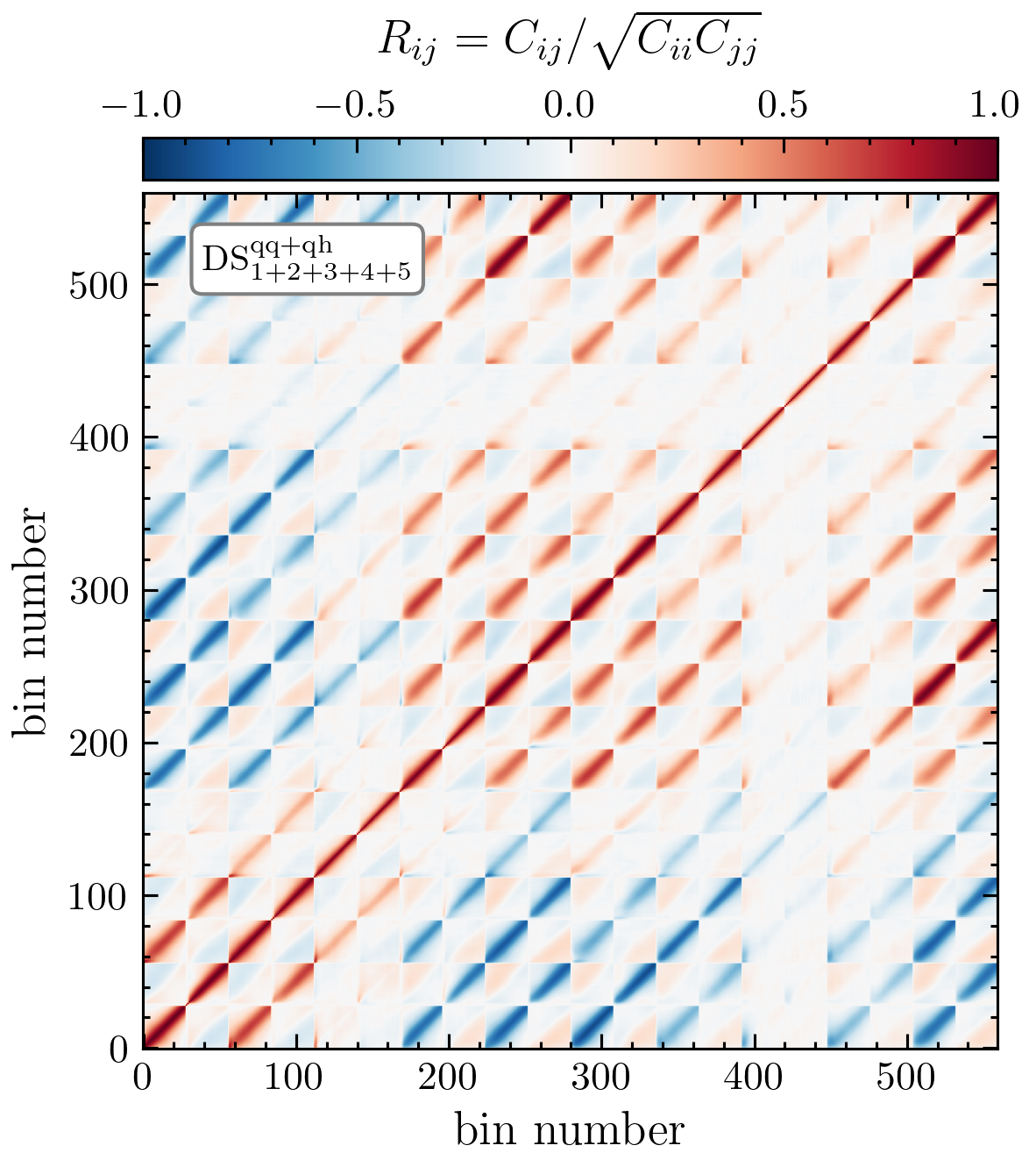
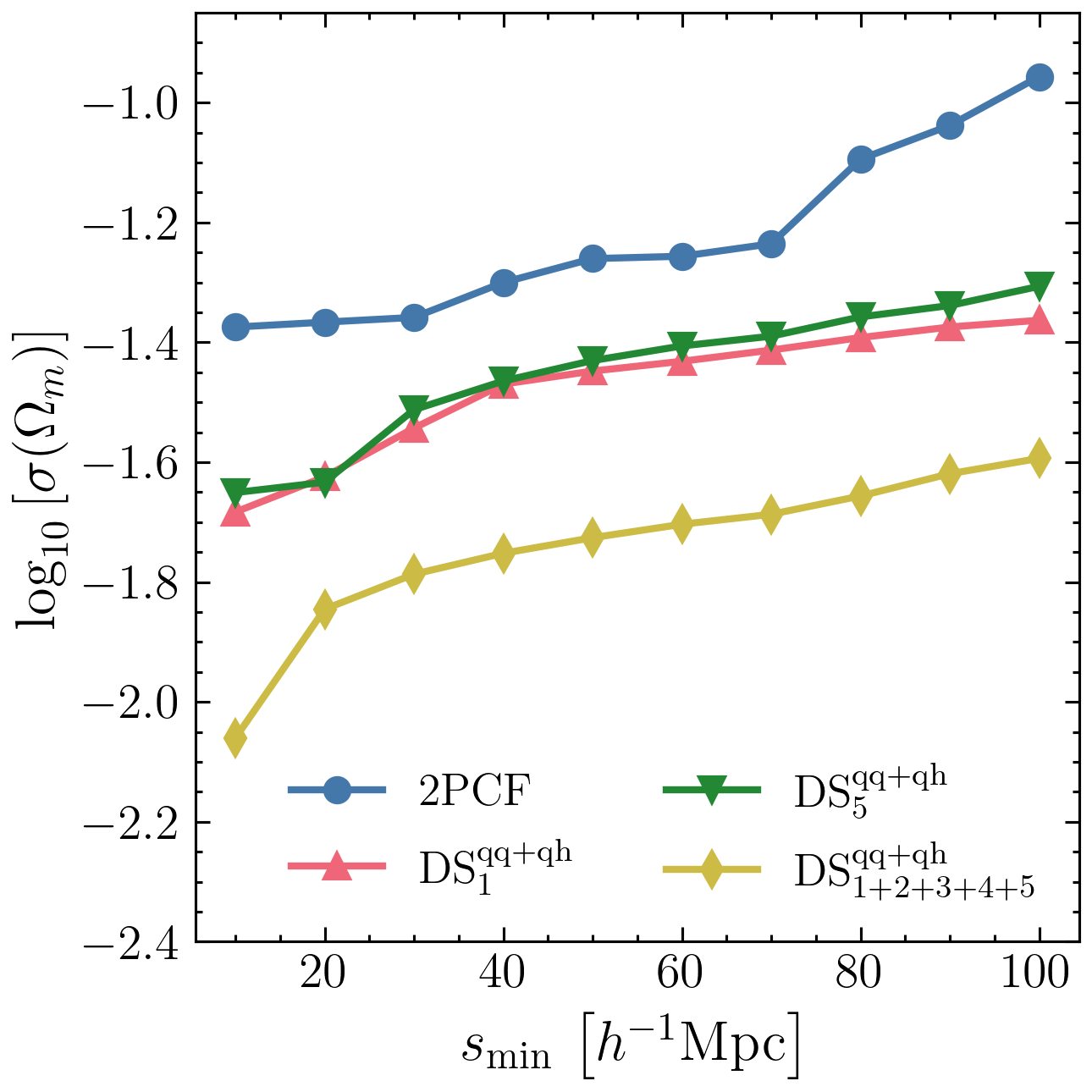
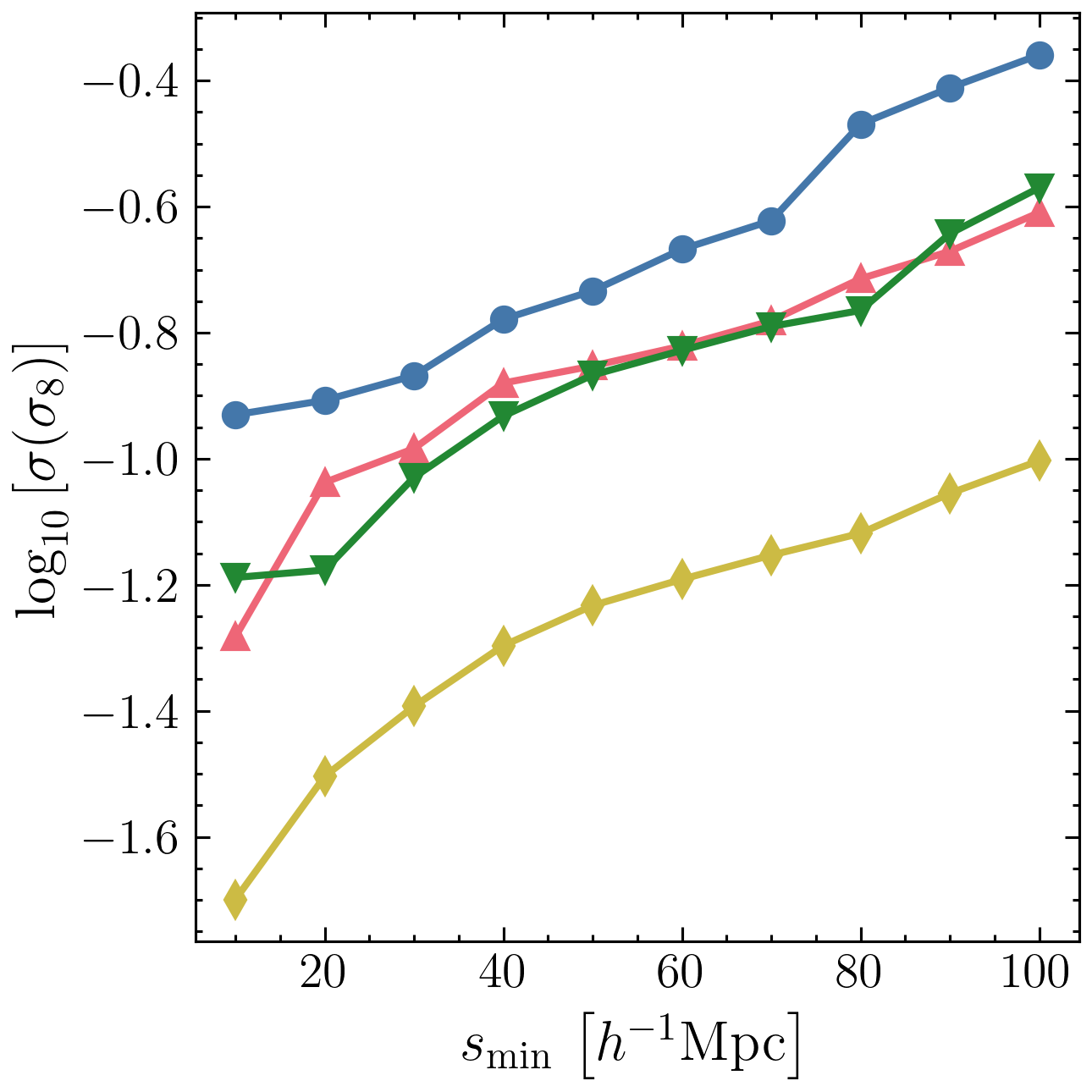
Where does the information come from?
?
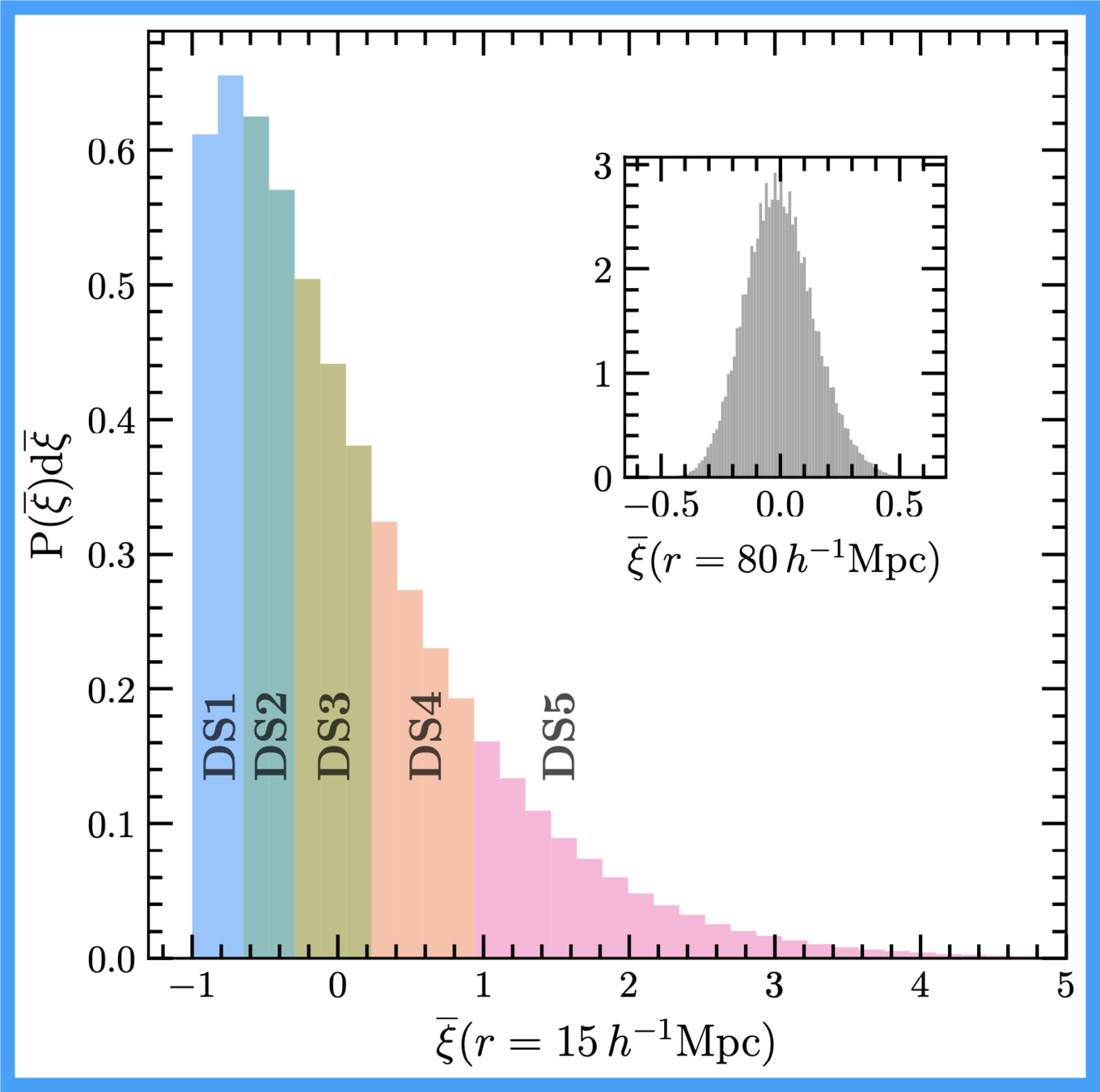
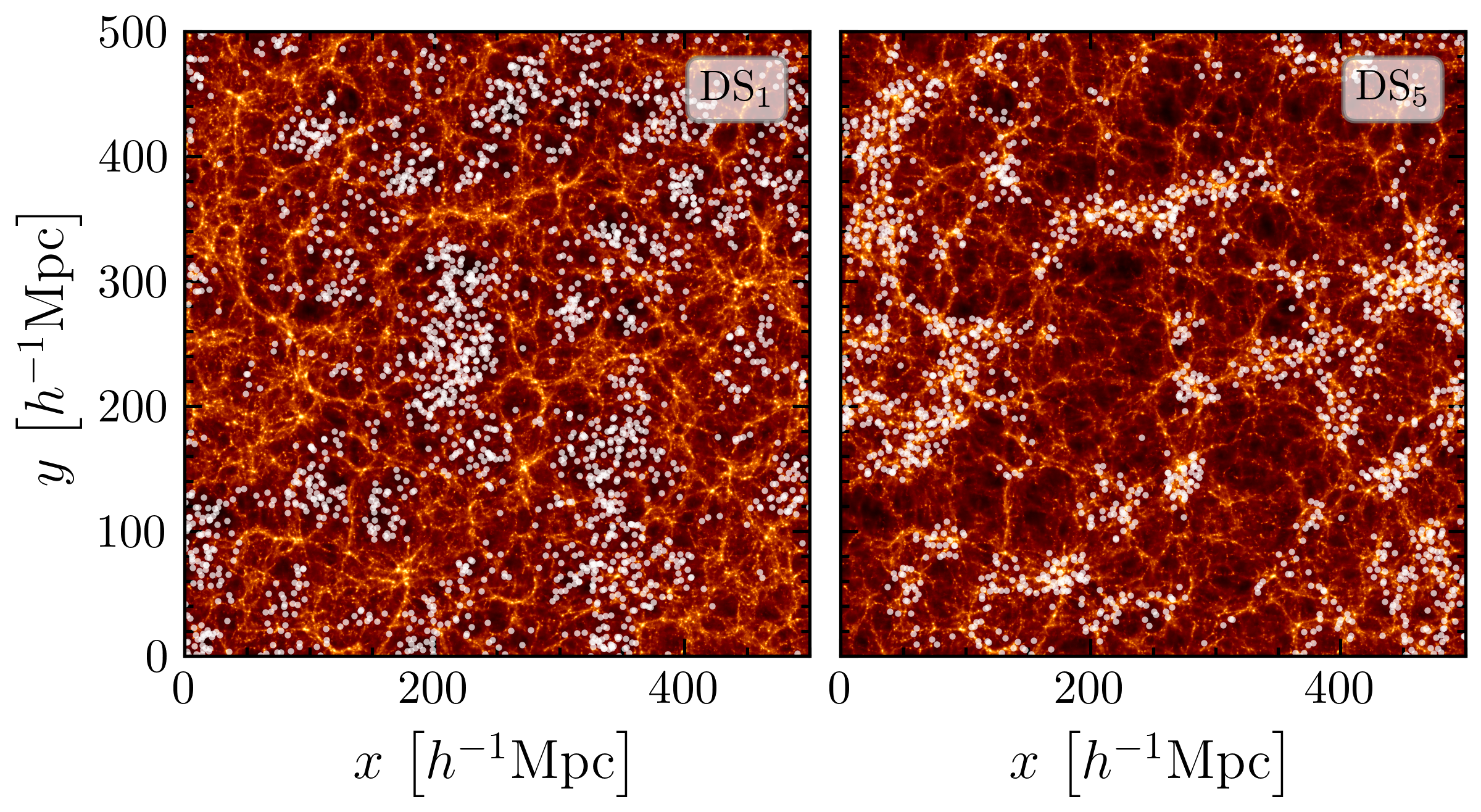
Density split in a Gaussian Random Field
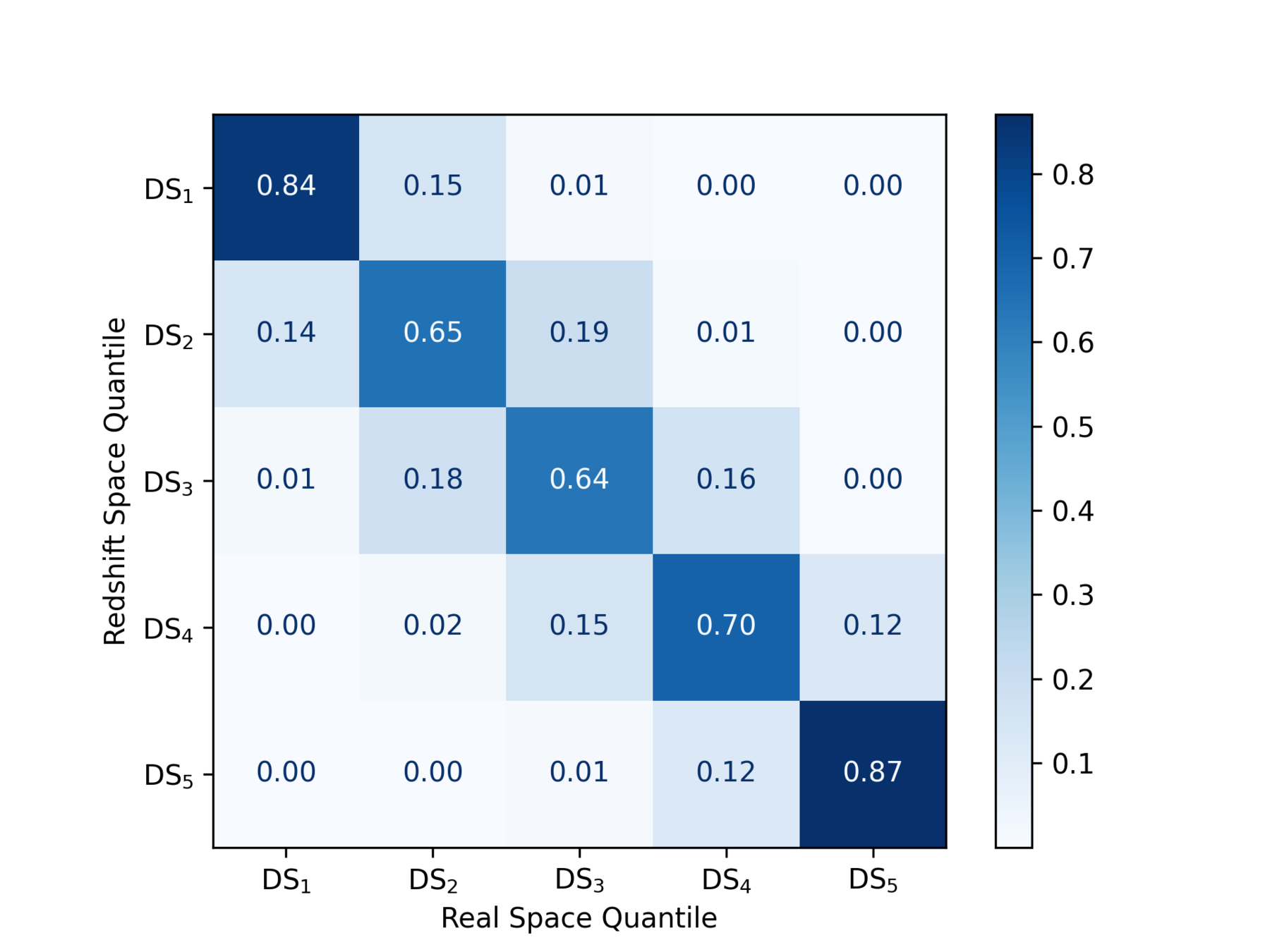
But, can we estimate densities realistically?
?
Real
Redshift
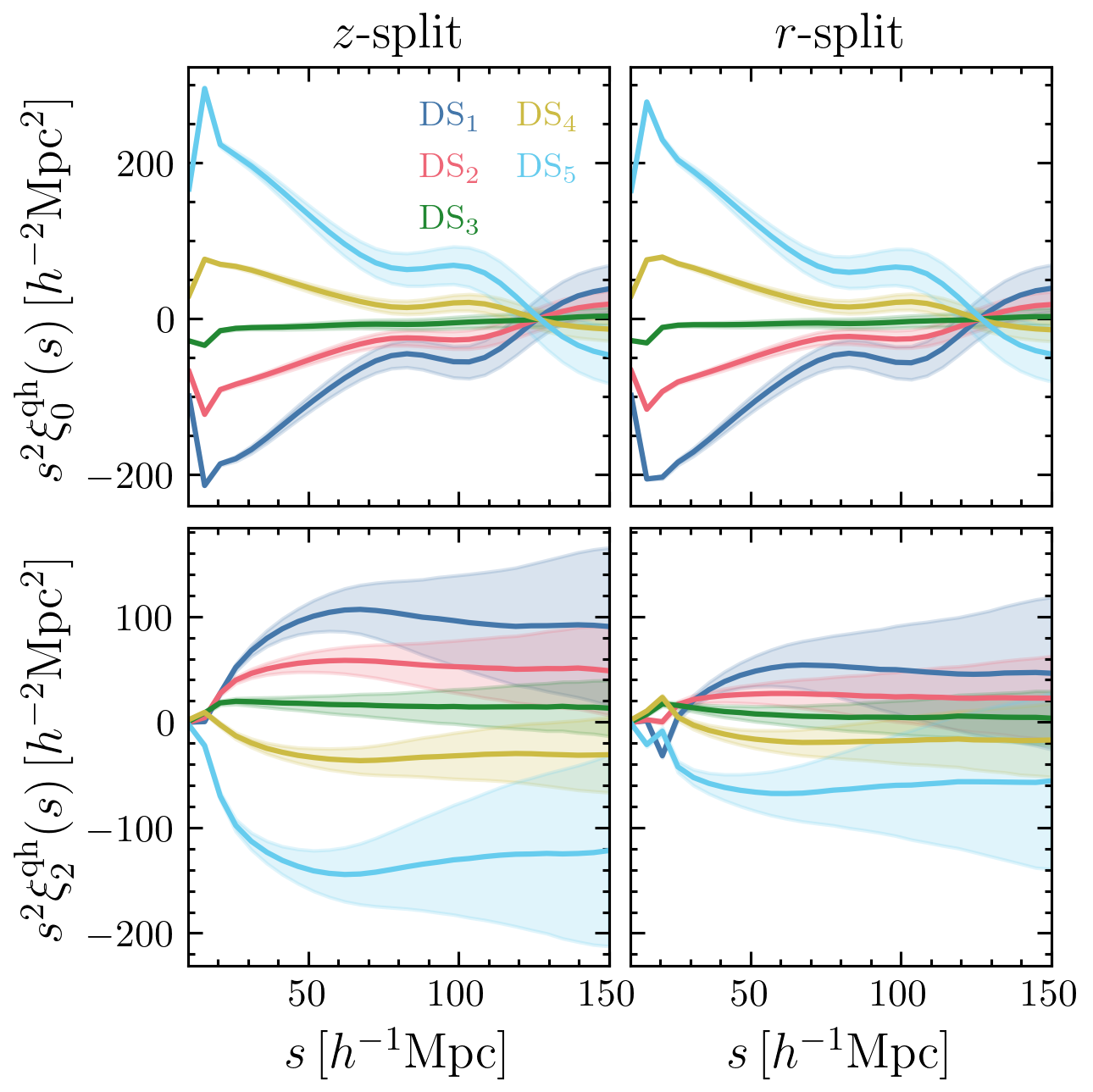
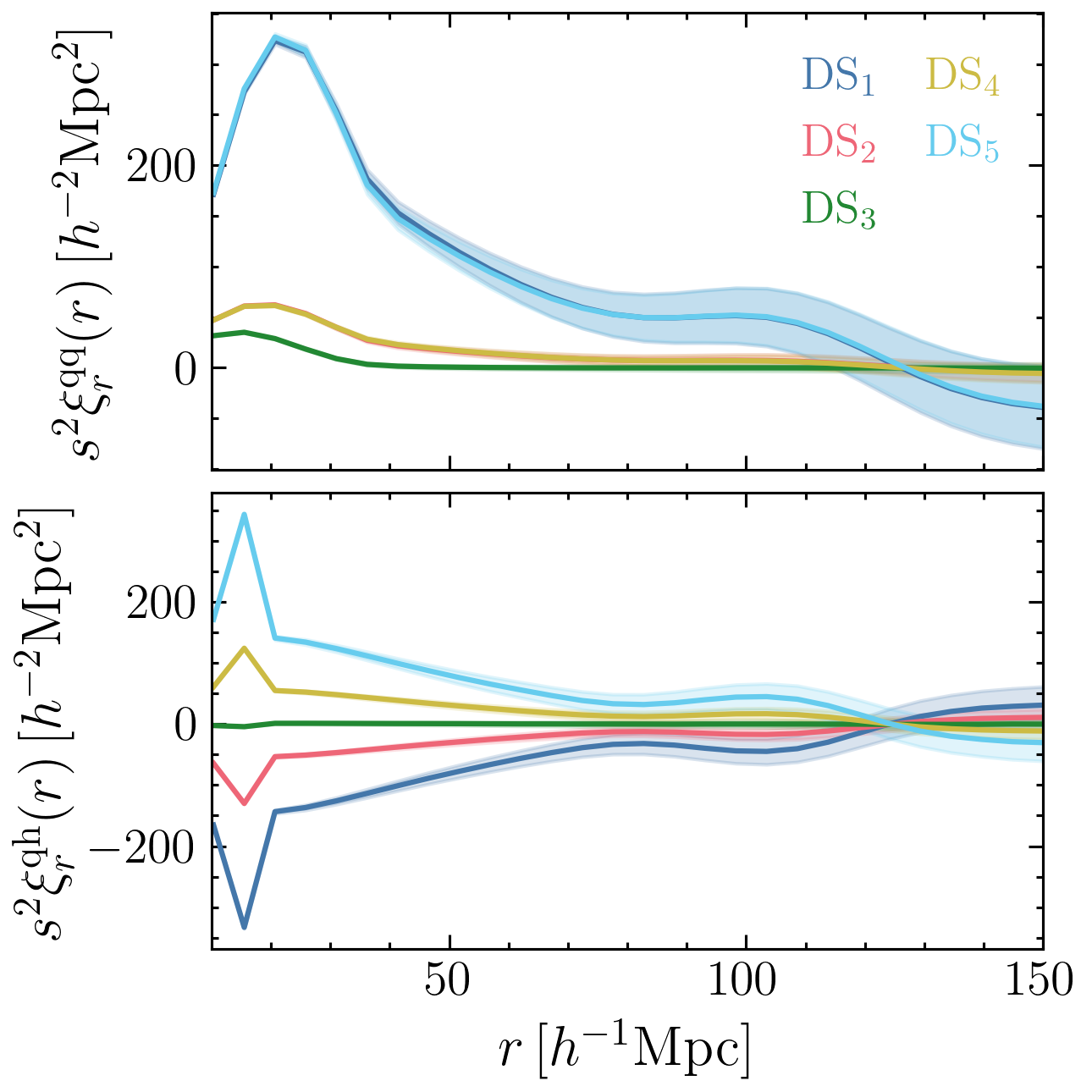
Cross-correlation between quintiles and haloes
Monopole
Quadrupole
s^2
s^2
Monopole
Quadrupole
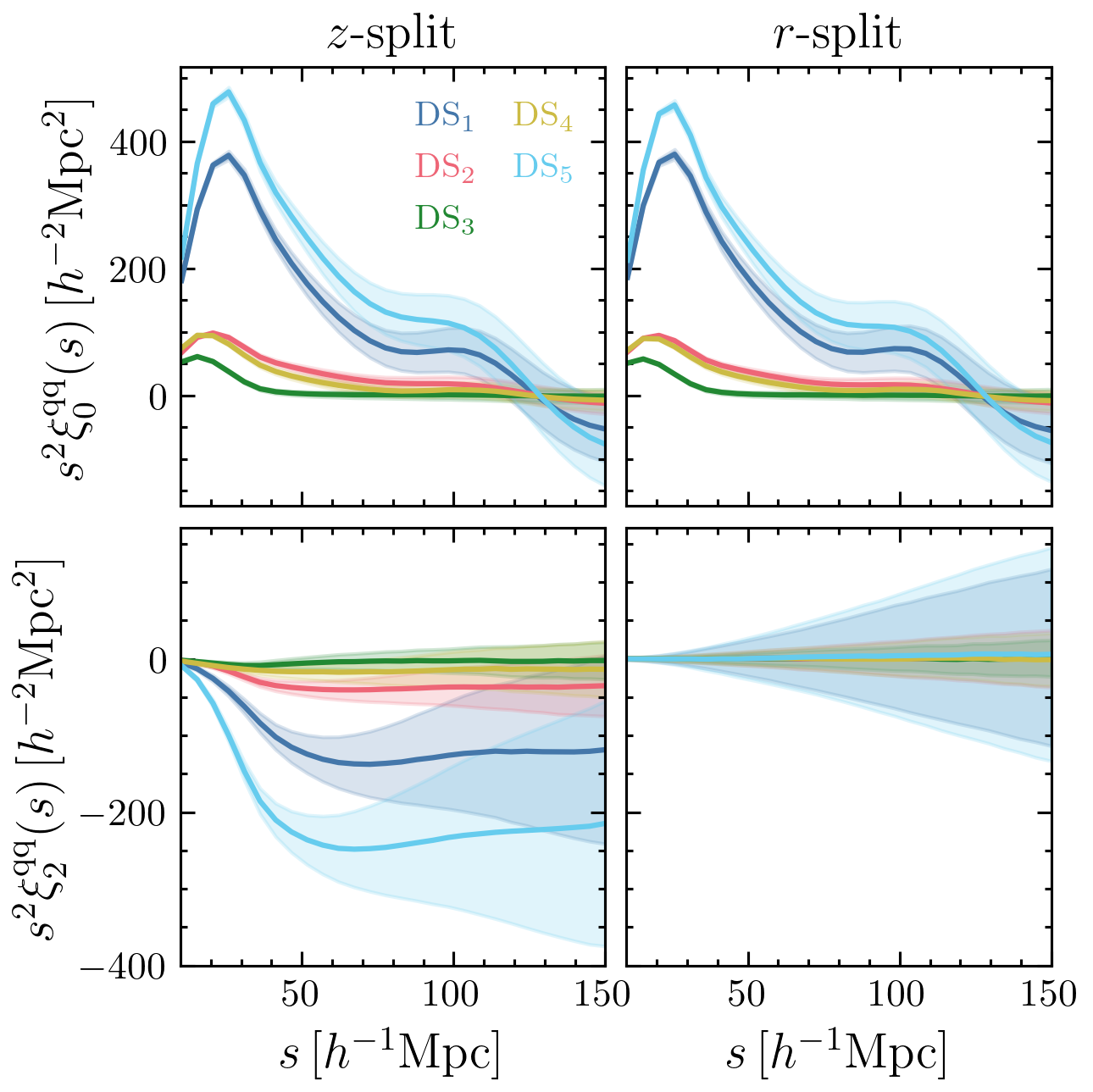
Autocorrelation of quintiles
s^2
s^2
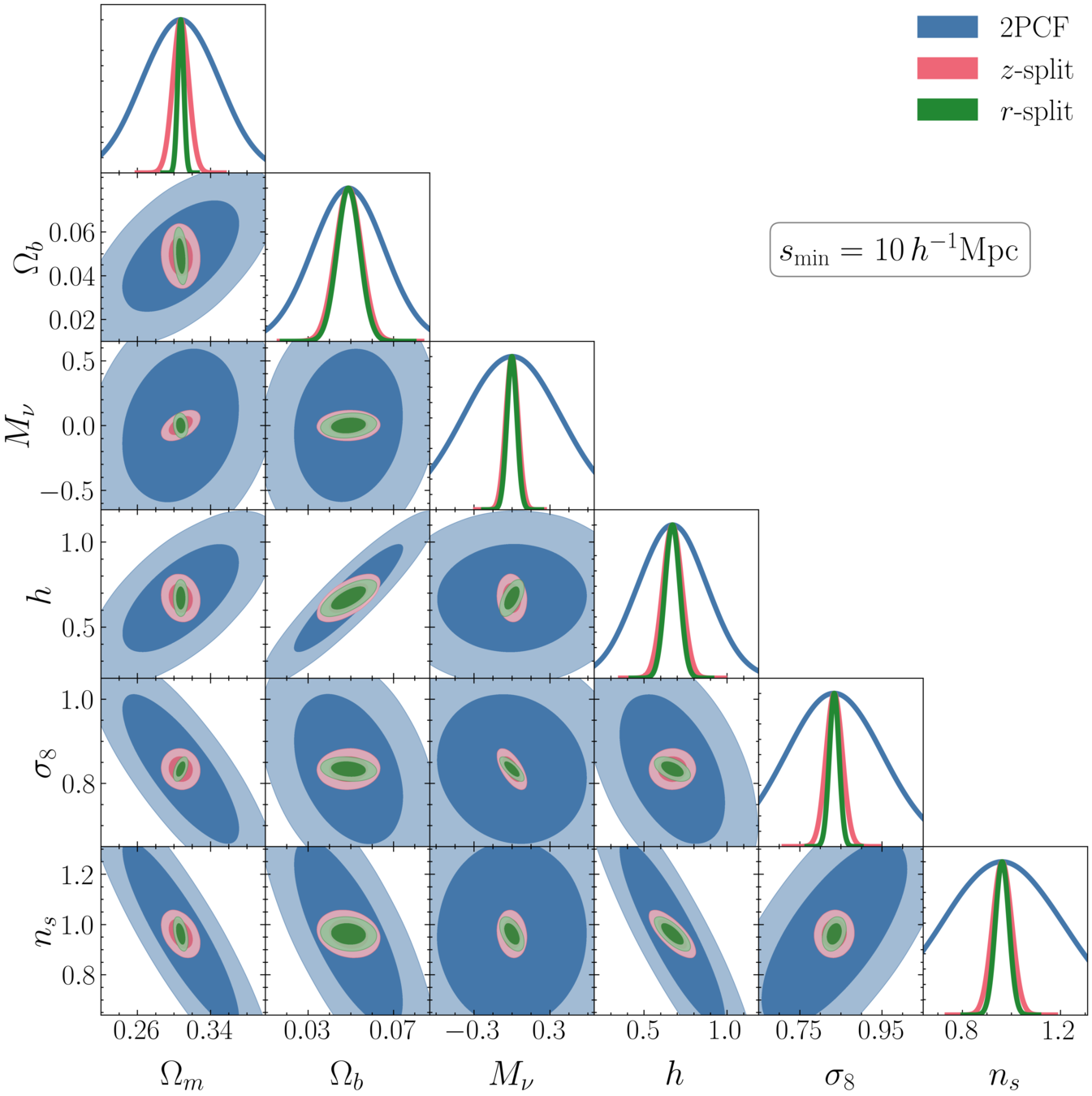
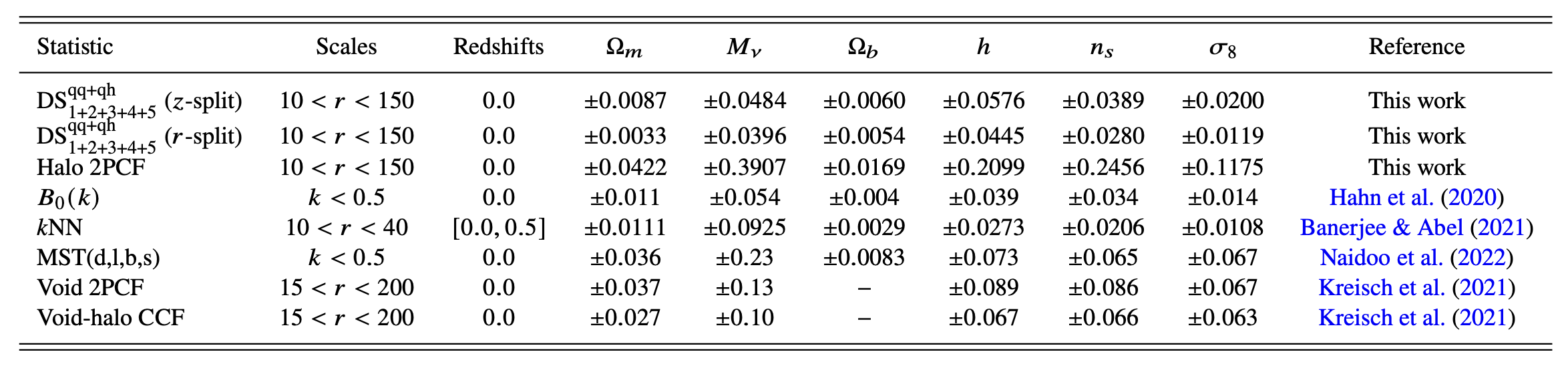
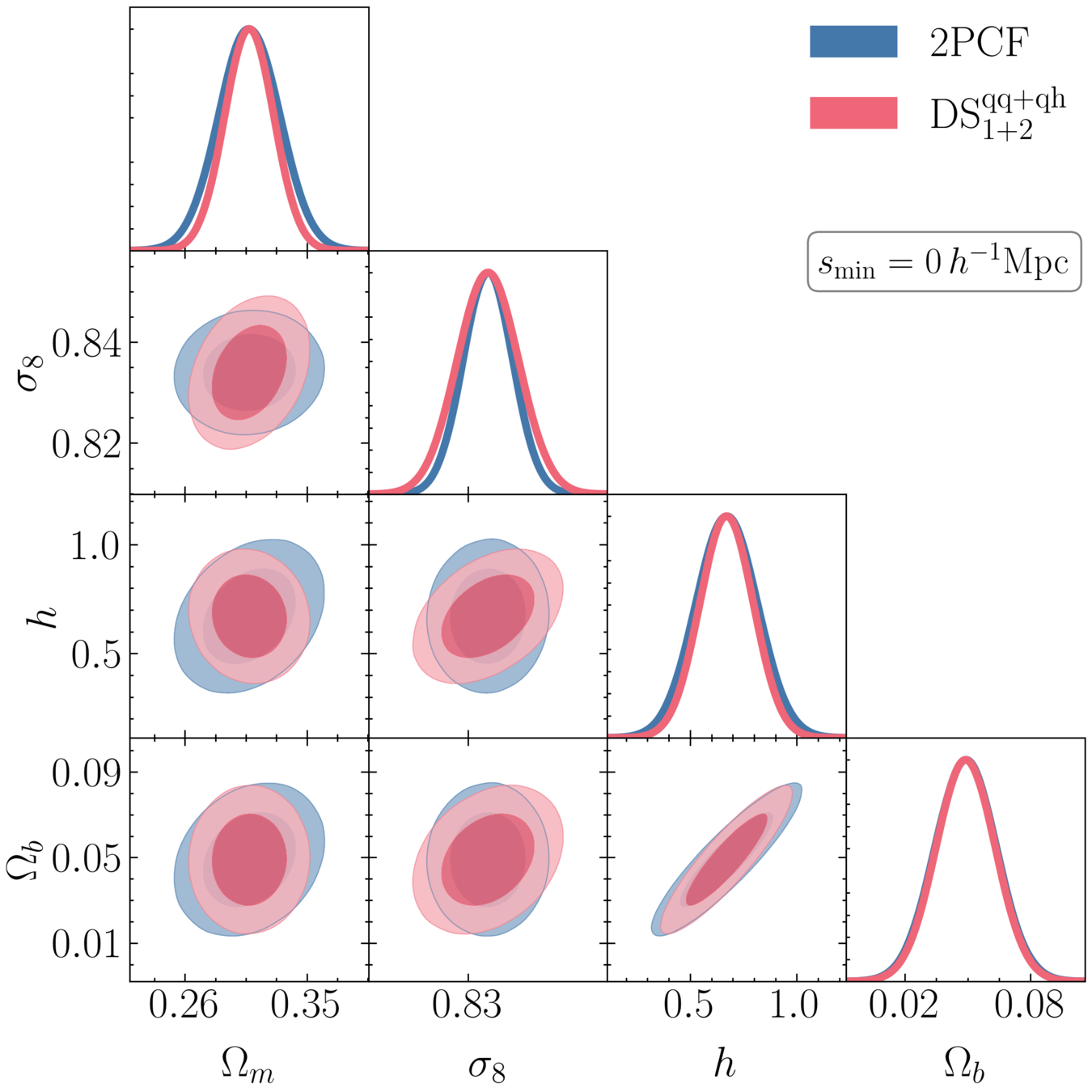
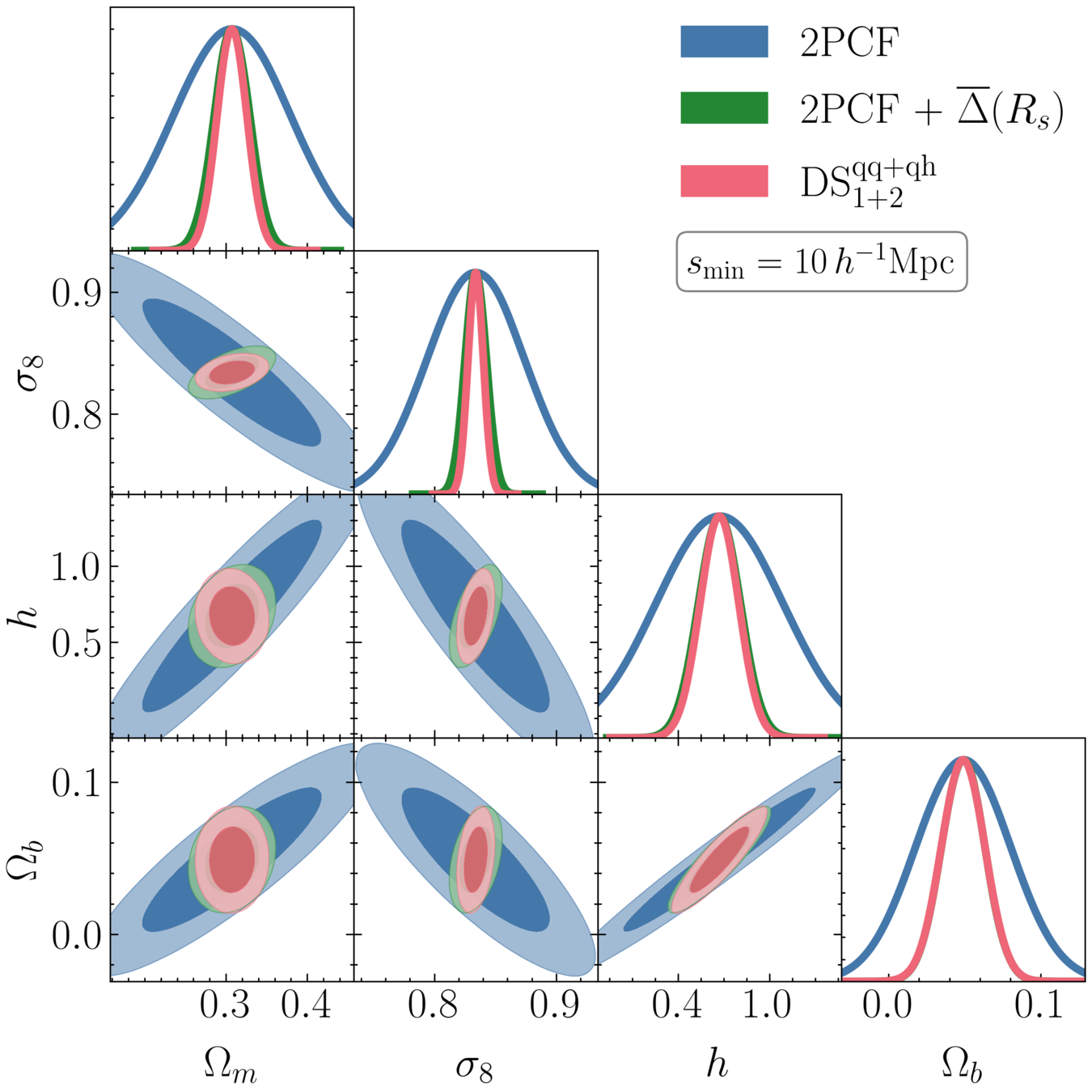
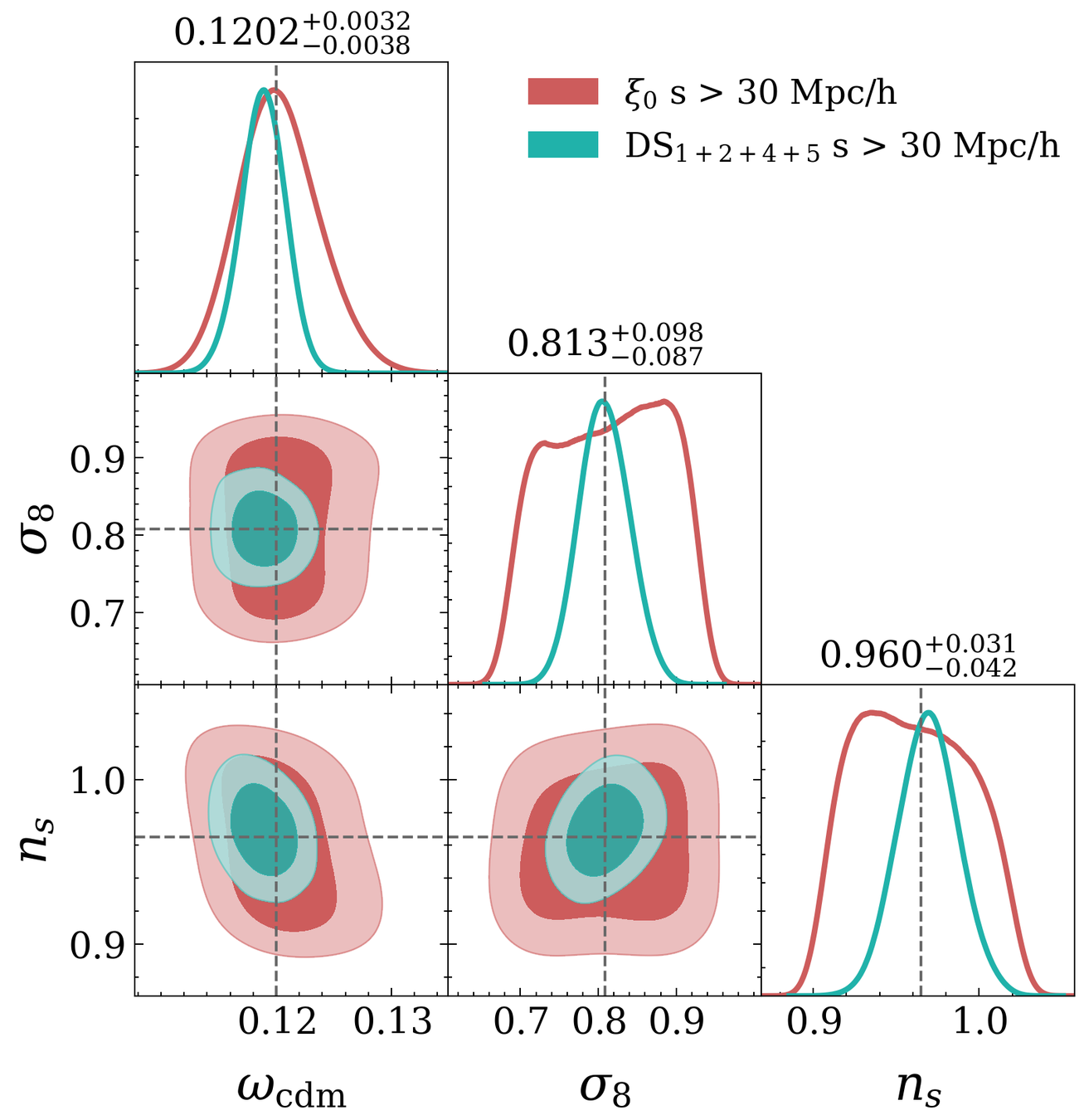
Comparison against other works that have used the same set of tracers
\theta
Simulated Data
Data
Prior
Posterior
x_\mathrm{obs}
x
P(\theta|x_\mathrm{obs})
Inverse problem
Forwards model
+ Galaxy-Halo connection
+ Cut-sky
+ Lightcone
+ Alcock-Paczinsky
+ Fiber collisions
Forward Model
N-body simulations
Observations
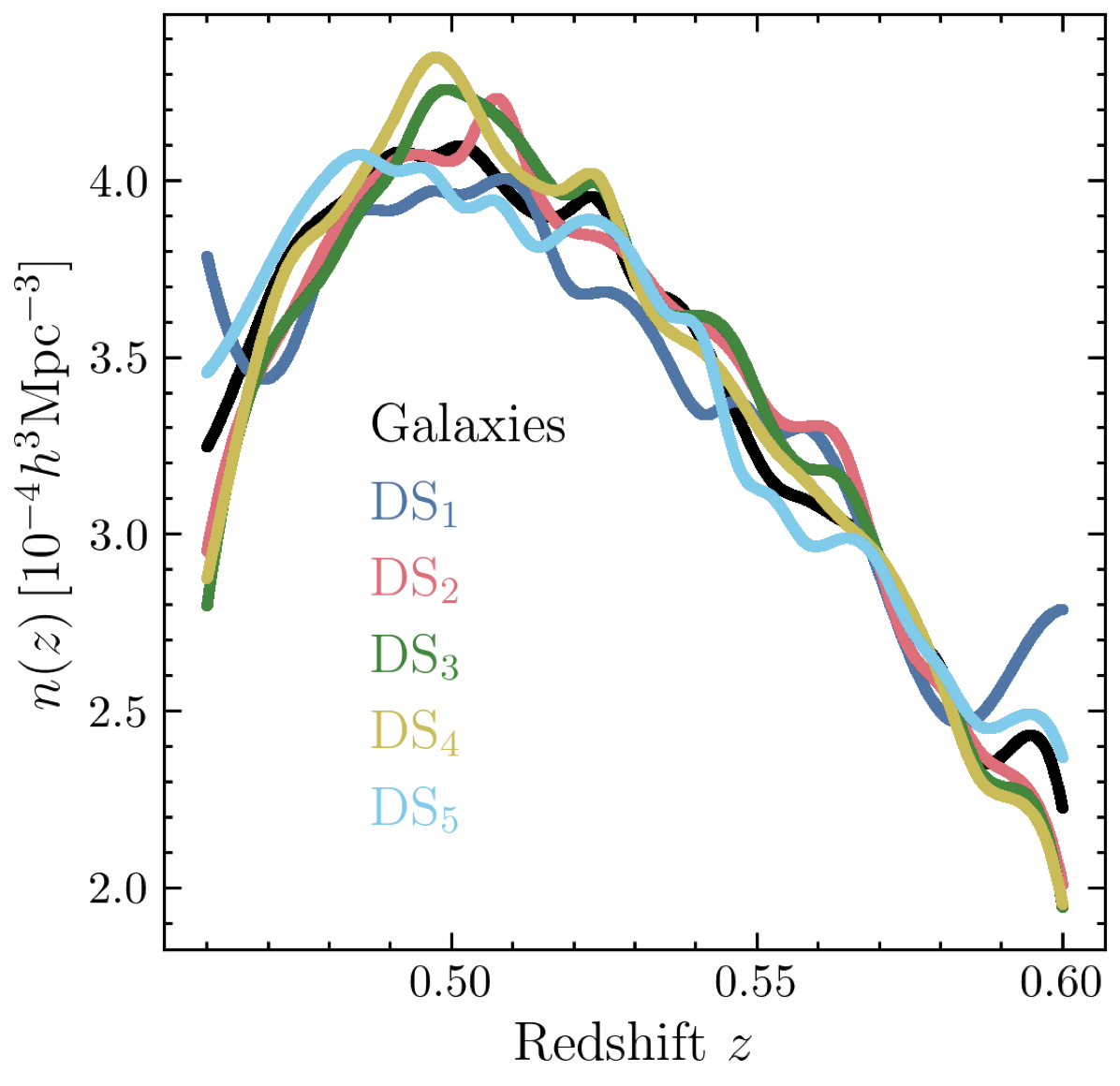
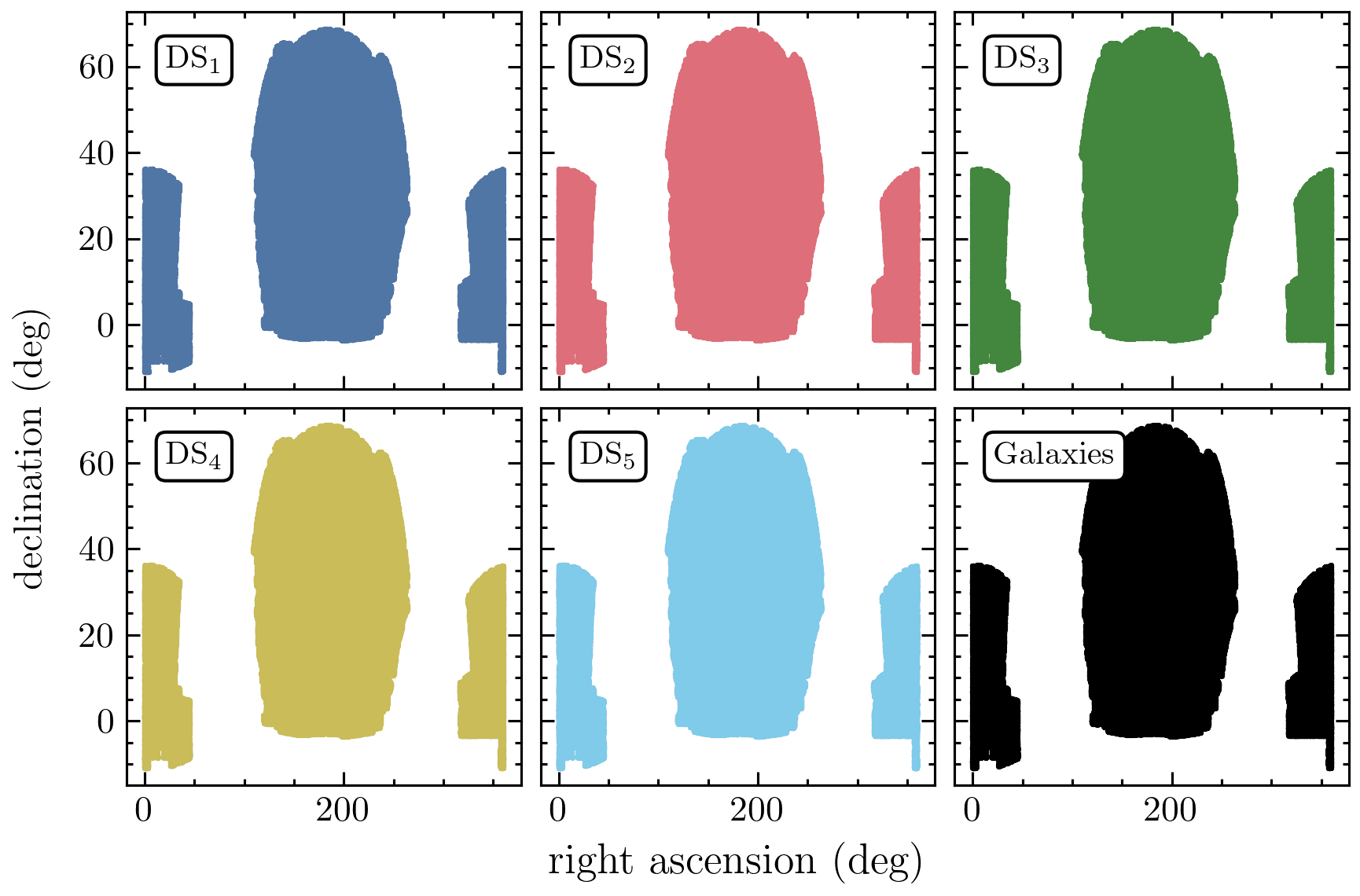
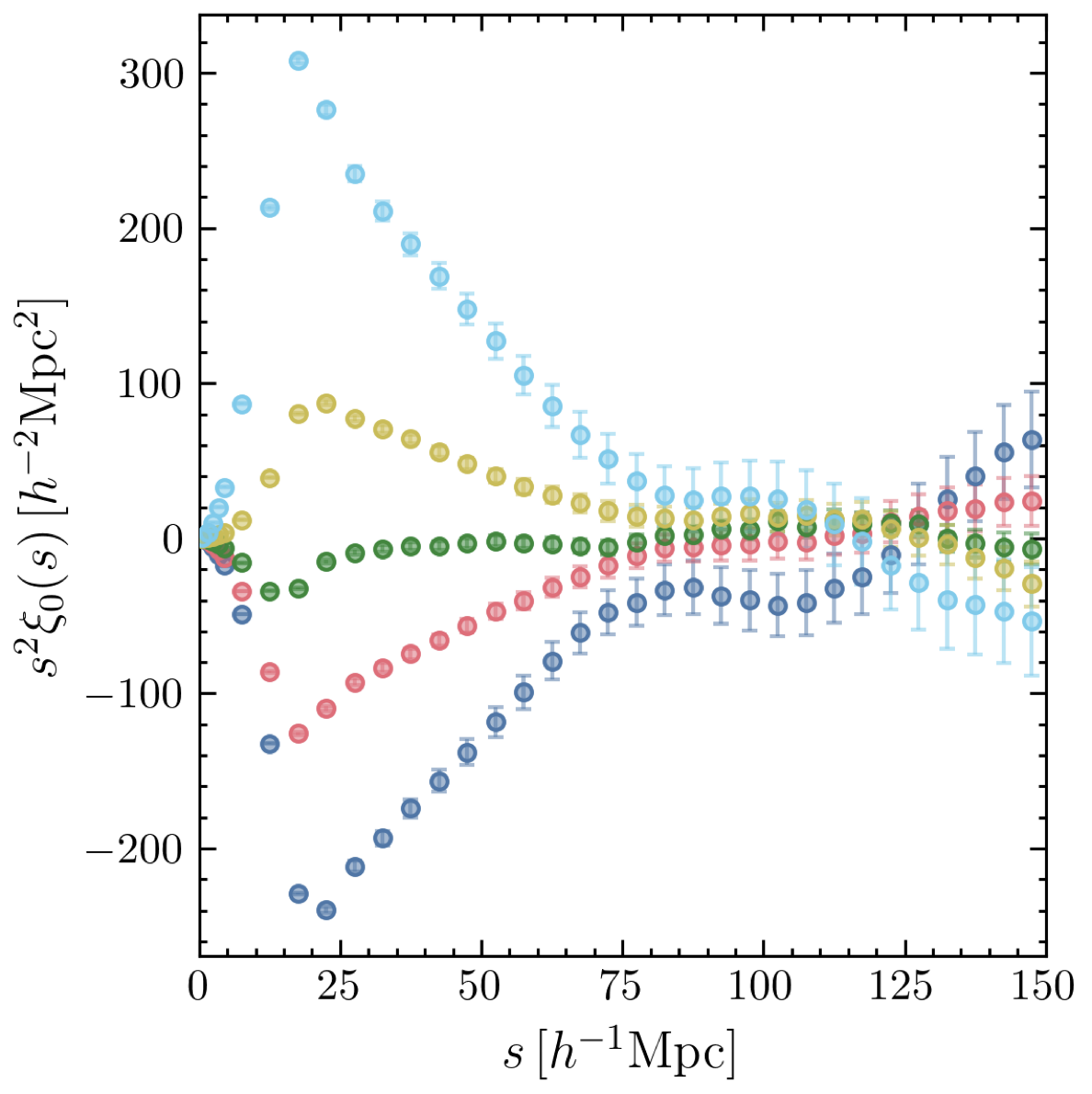
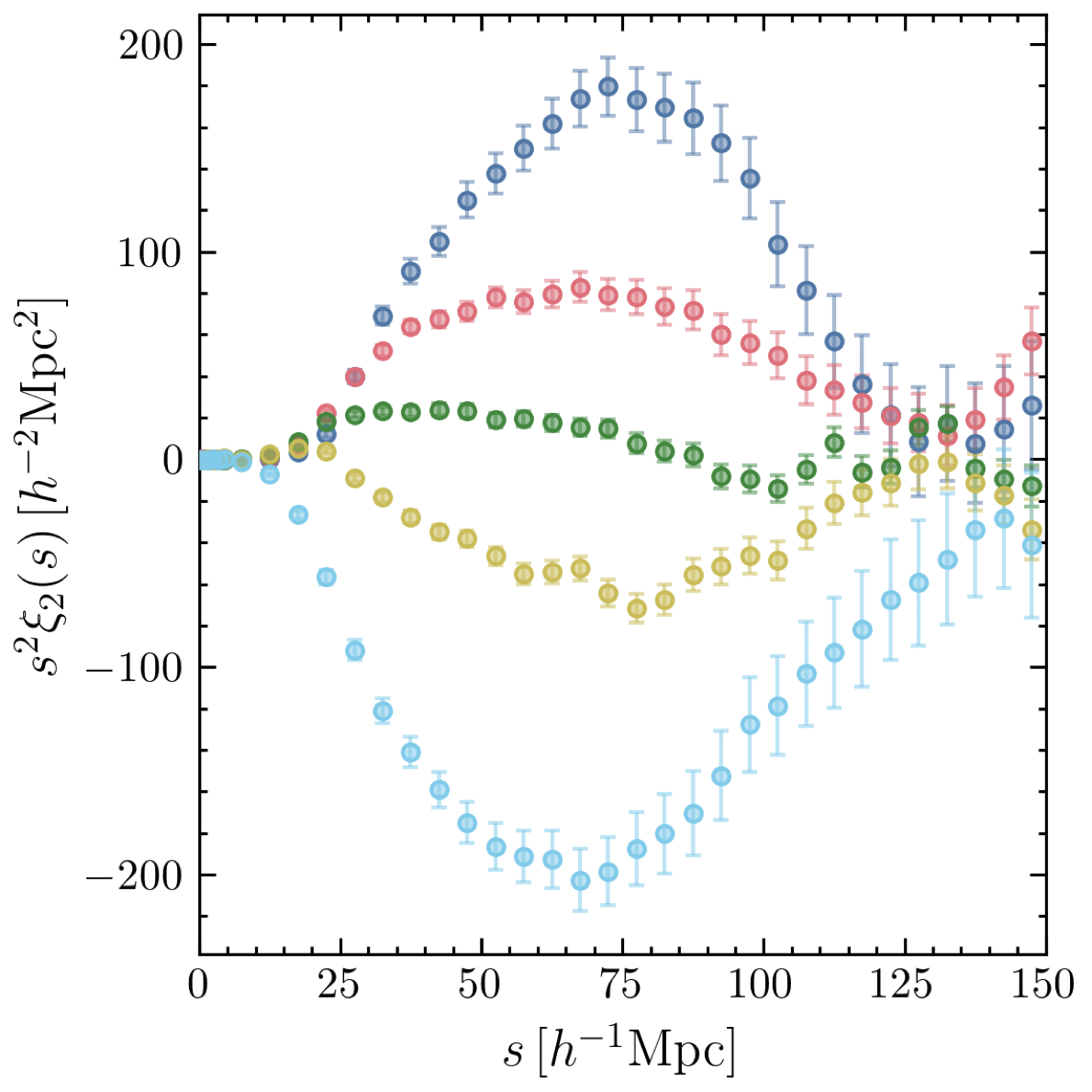
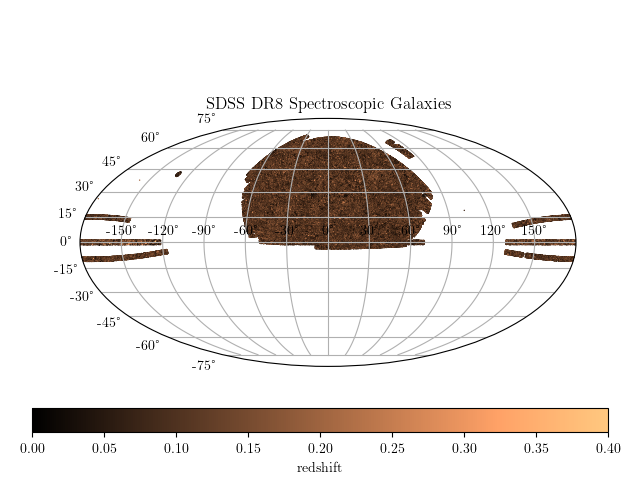
Density split in a SDSS BOSS
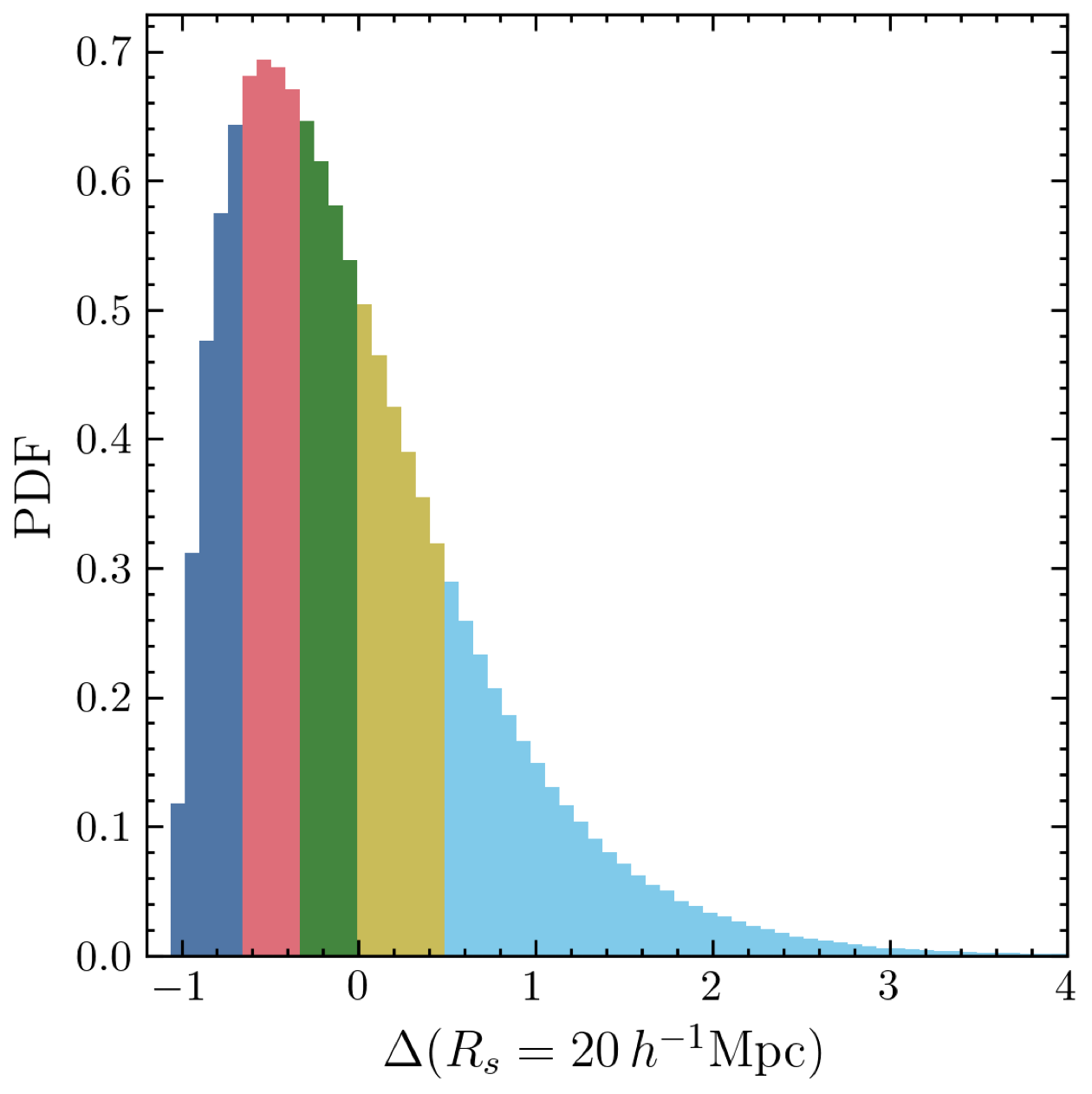
CMASS 0.46 < z < 0.6
Galaxy-Halo connection
Main Assumptions
- Galaxies don't impact dark matter clustering
- Number of galaxies depends on halo mass only
Extensions: Get creative!
But these extensions might limit our constraining power
a) Use hydro simulations to limit options
b) Mask the data to optimise robustness?
Velocity bias
Assembly bias
Environment
Concentration
Formation time
...
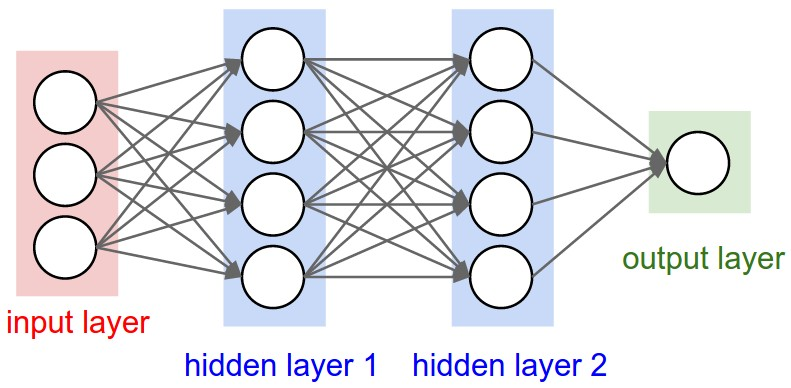
Credit: https://cs231n.github.io/convolutional-networks/
S(r)
\Omega_m
\Omega_\Lambda
...
\log(\mathcal{L}) \propto (S - S_\mathrm{obs}) C^{-1}(S - S_\mathrm{obs})
Neural Network emulator
\mathcal{O}(100) \,\,\, \mathrm{Nbody \, simulations}
Implicit likelihood inference with normalising flows
x = f(z), \, z = f^{-1}(x)
p(\mathbf{x}) = p_z(f^{-1}(\mathbf{x})) \left\vert \det J(f^{-1}) \right\vert
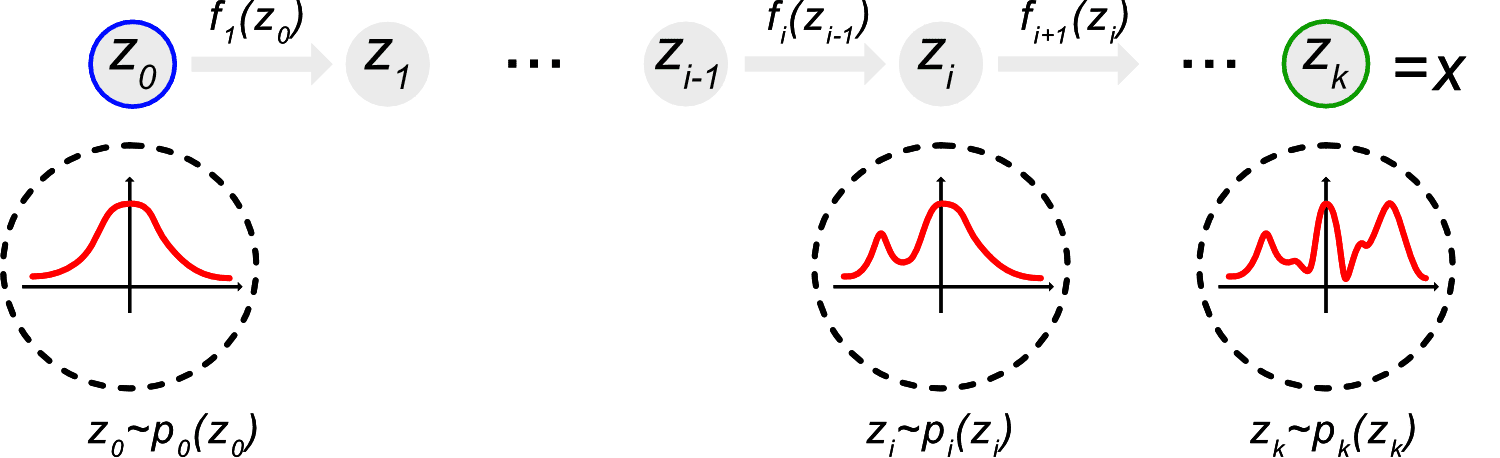
No assumptions on the likelihood (likelihoods rarely Gaussian!)
No expensive MCMC chains needed to estimate posterior
\Omega_M
\Omega_\Lambda
\sigma_8
Input
x
Neural network
f
Representation
(Summary statistic)
r = f(x)
Output
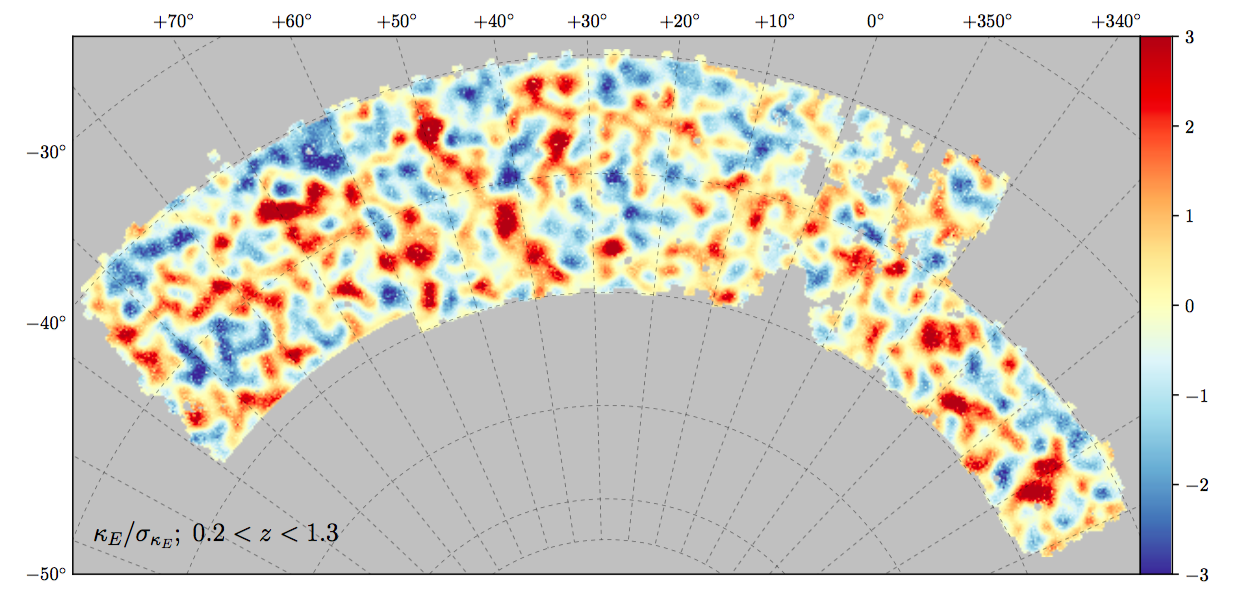
Increased interpretability through structured inputs
Modelling cross-correlations
P(\theta|x_\mathrm{obs})
What ML can do for cosmology
- ML to accelerate non-linear predictions and density estimation
- Can ML extract **all** the information that there is at the field-level in the non-linear regime?
- Compare data and simulations, point us to the missing pieces?
cuestalz@mit.edu
Copy of Copy of DensitySplit
By carol cuesta
