Big Data Cosmology meets AI
IAIFI Fellow
Carol Cuesta-Lazaro
MIT - 29th April 2024
Video Credit: N-body simulation Francisco Villaescusa-Navarro
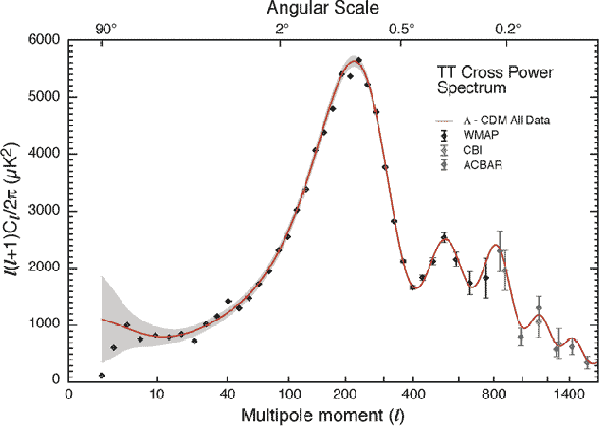
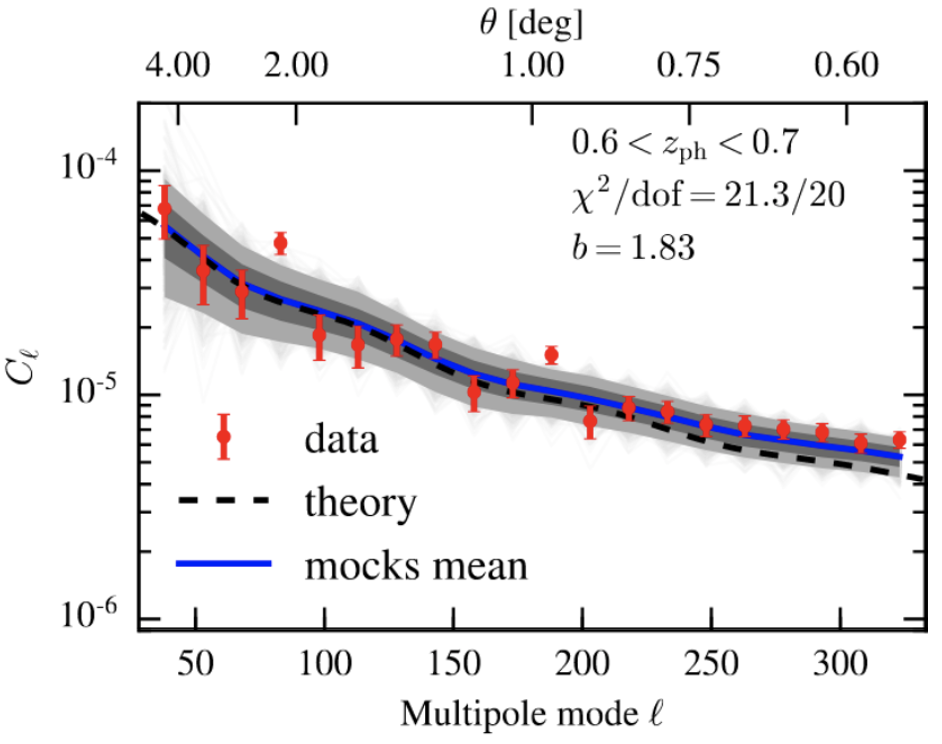
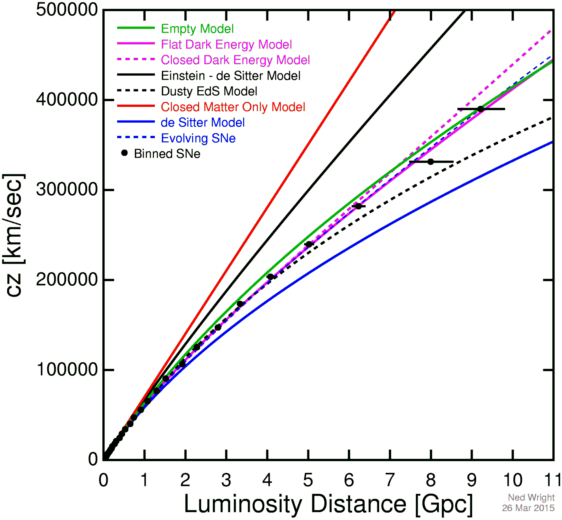
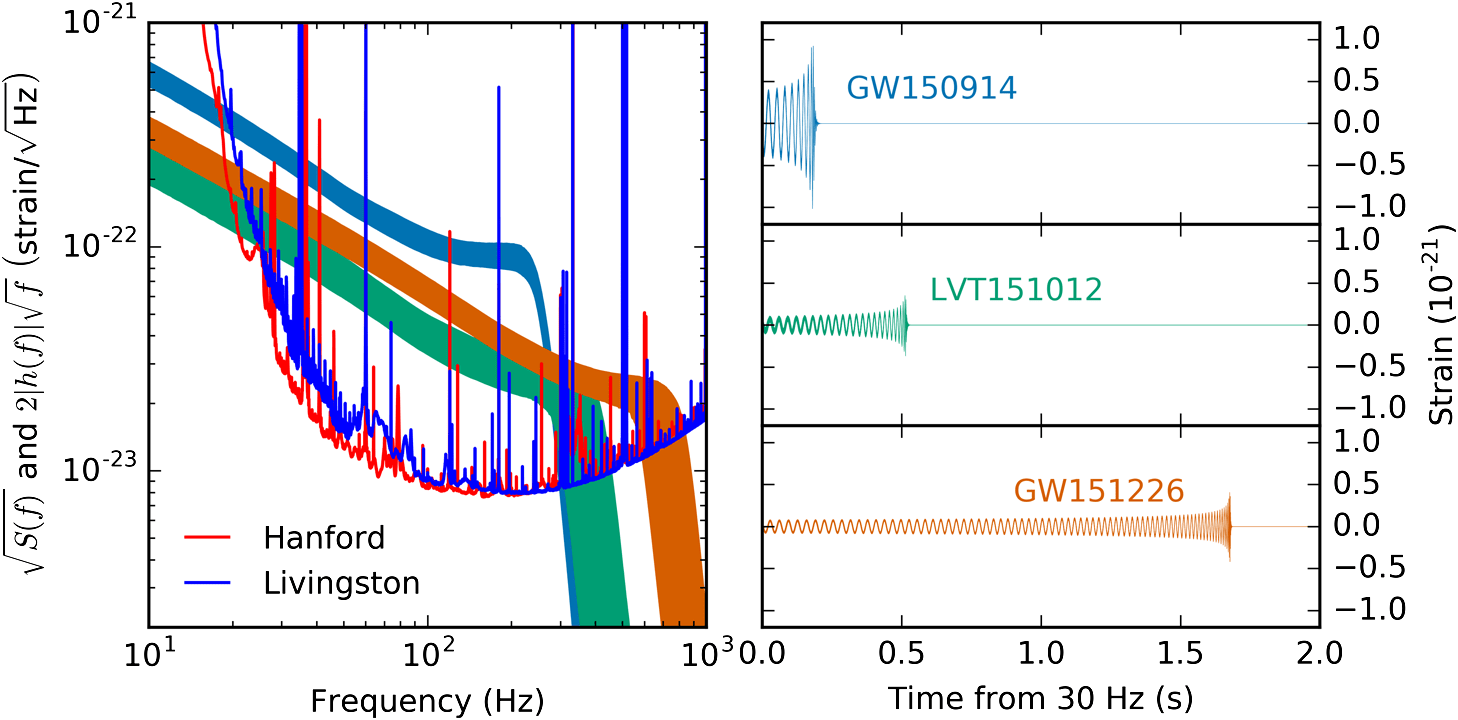
The era of Big Data Cosmology
1-Dimensional
Machine Learning
Secondary anisotropies
Galaxy formation
Intrinsic alignments
Dust
xAstrophysics
DESI, DESI-II, Spec-S5
Euclid
LSST
Simons Observatory
CMB-S4
Ligo
Einstein
LSST
Early Universe Inflation
{\delta_\mathrm{Initial}}
Late Universe
Energy and matter content
Evolution
{\delta_\mathrm{Final}}
\color{darkgray}{\Omega_m}
Dark matter
Dark energy
\color{darkgreen}{w_0, w_a}
\color{darkolive}{H_0}
Hubble Constant
\color{darkred}{\Omega_b}
\color{darkblue}{\sum m_\nu}
Baryons
Neutrino masses
\color{purple}{f_\mathrm{NL}}
\color{darkorange}{n_s}
Non-Gaussianity
Tilt power spectrum
Hubble tension
Beyond the Standard Model
Multifield Inflation
2
3
Hybrid ML - Physics Simulators
Unsupervised searches
1
Cosmological (field level) Inference for Galaxy Surveys
DESI
DESI: Dark Energy Spectroscopic Instrument
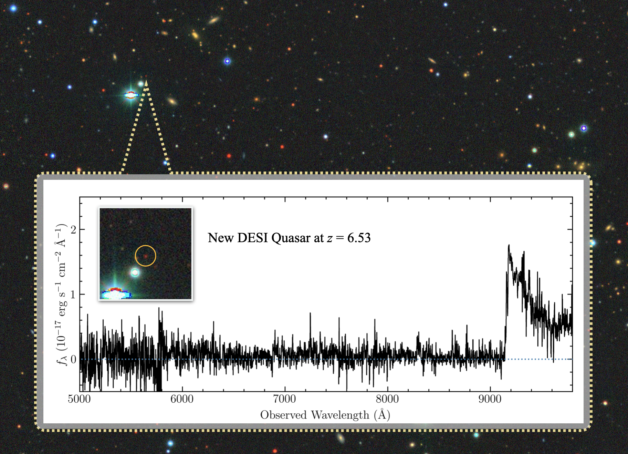
~40 Million spectra!
(Image Credit: Jinyi Yang, Steward Observatory/University of Arizona)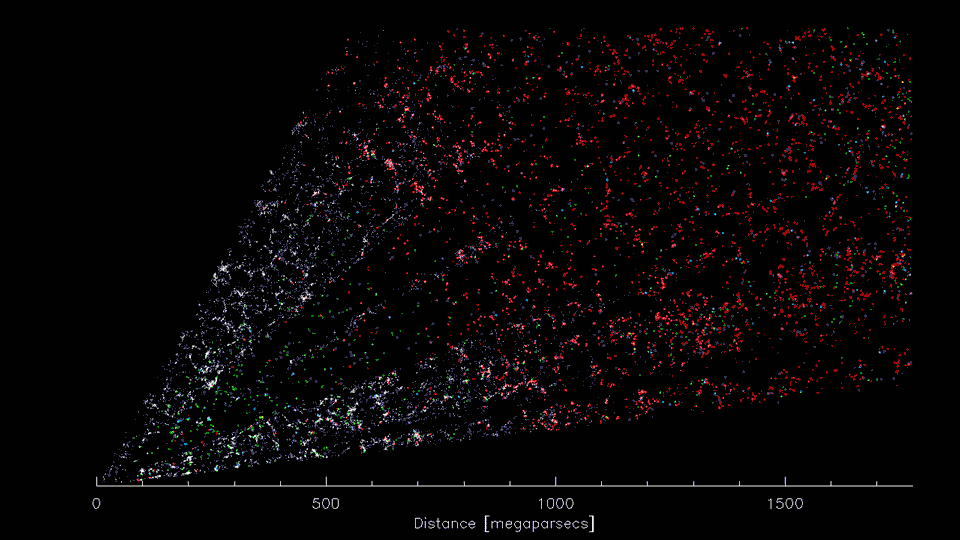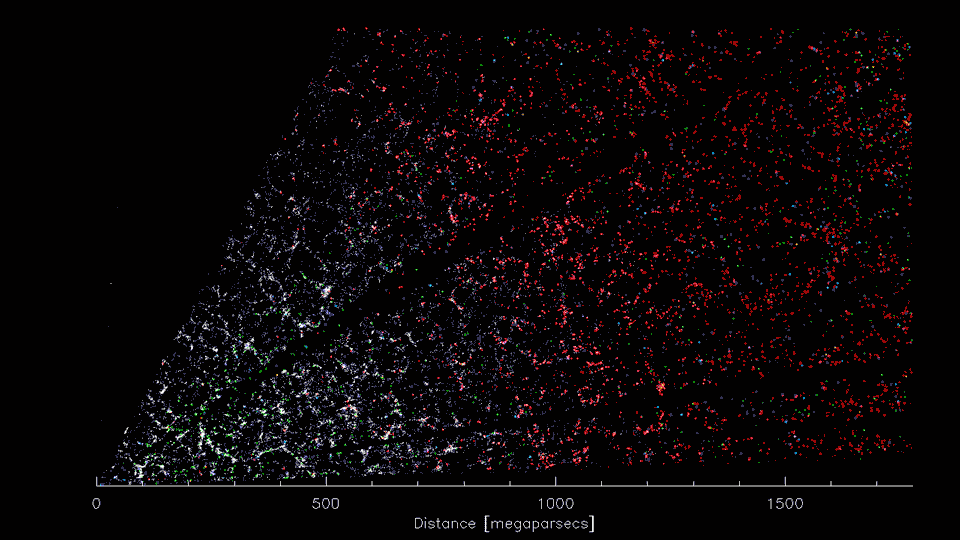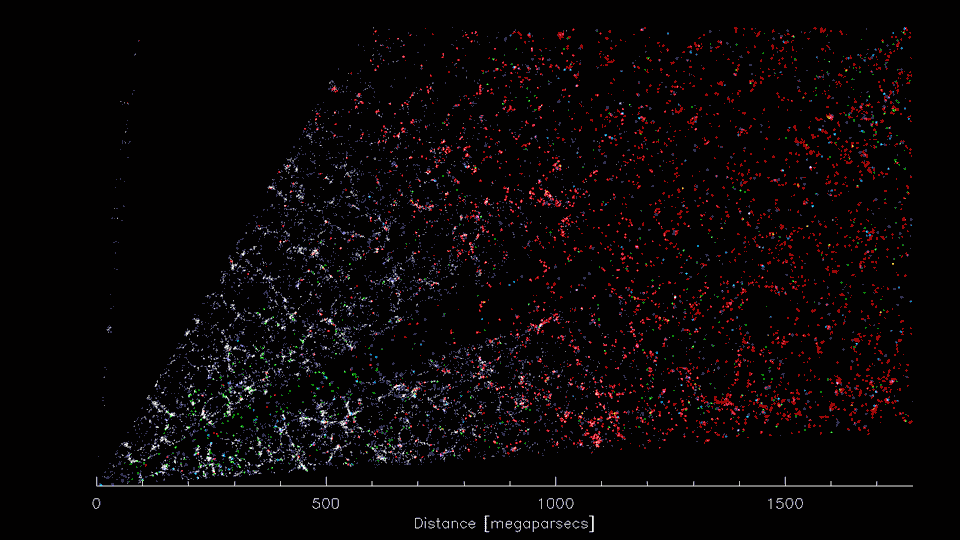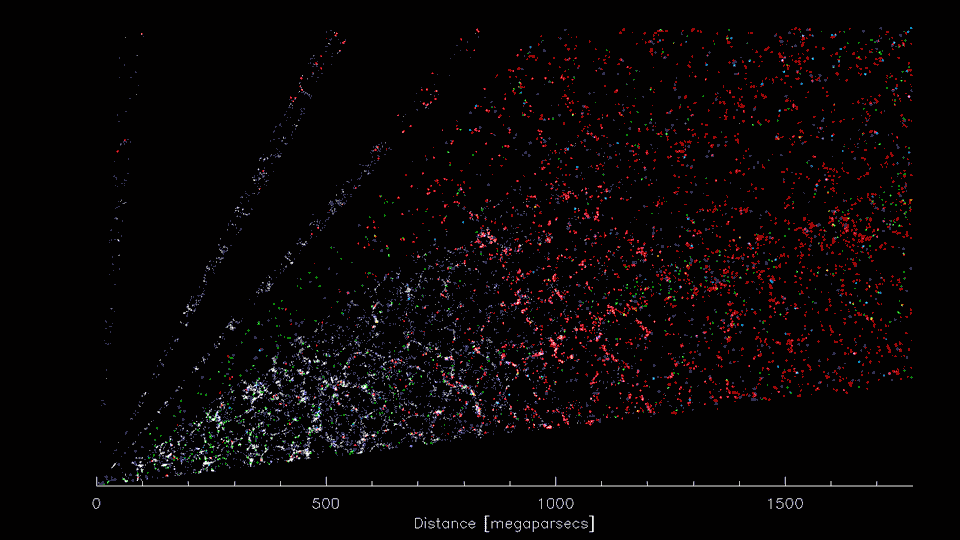
(Image Credit: D. Schlegel/Berkeley Lab using data from DESI)
High dimensional data
x
Unknown
p(x|\mathcal{C})
Simple summary statistic
s
p(s|\mathcal{C})
estimated with Perturbation Theory
Probability pair of galaxy
Pair separation
\theta
Forward Model
Parameters
Observable
x
Likelihood
p(\mathcal{\theta}|x)
Simulator
+ MCMC hammer
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...
Dark matter
Dark energy
Inflation
Perturbation Theory
Pen and paper
p(x|\mathcal{\theta})
+ Density Estimation
+ Sampler
p(\mathcal{\theta}|x) =
p(\theta) / p(x)
A forward model samples the likelihood
\theta
Parameters
Observable
x
Observed galaxy pointcloud
DESI
Forward Model
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...
Dark matter
Dark energy
Inflation
p(x|\theta) = \int dz p(x,z|\theta)
A 2D animation of a folk music band composed of anthropomorphic autumn leaves, each playing traditional bluegrass instruments, amidst a rustic forest setting dappled with the soft light of a harvest moon
Image credit: DALL·E 3
1024x1024
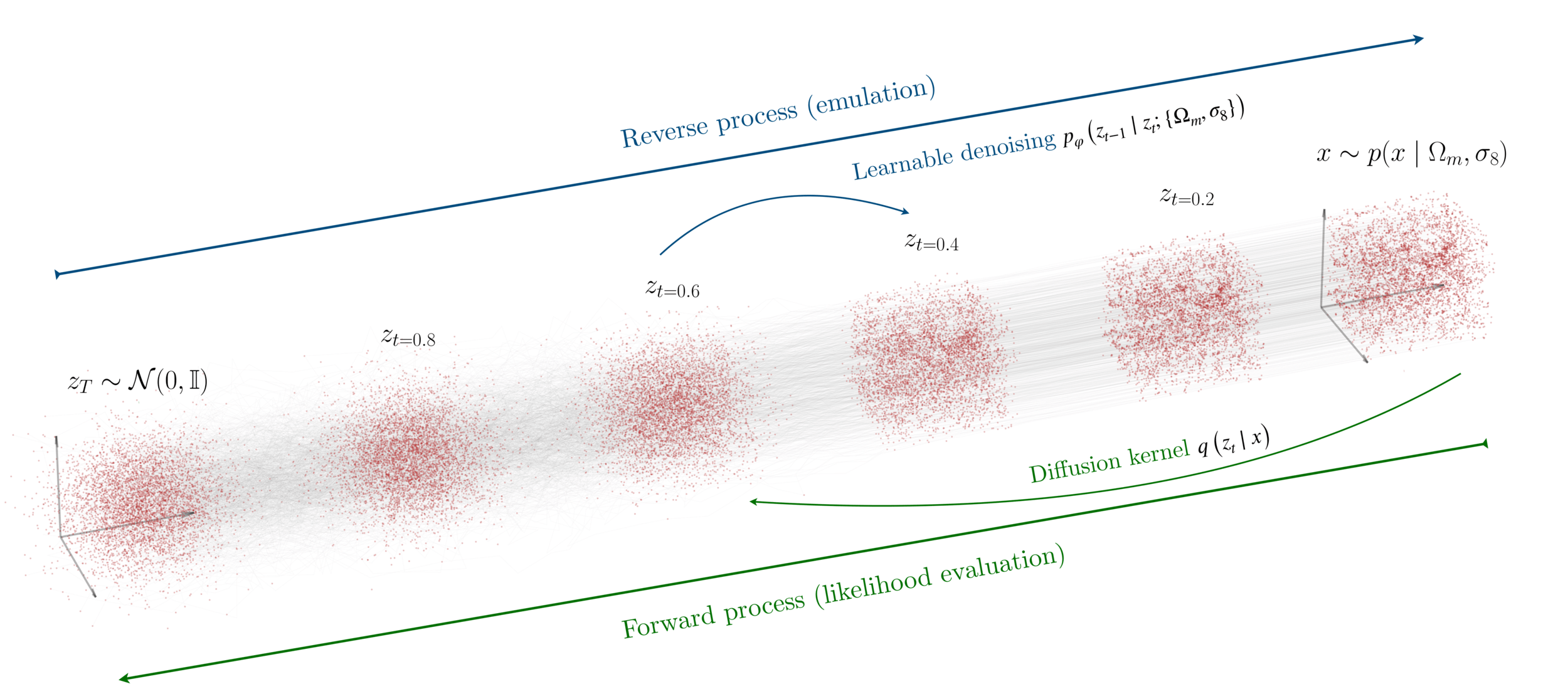
"A point cloud approach to generative modeling for galaxy surveys at the field level"
Cuesta-Lazaro and Mishra-Sharma
arXiv:2311.17141
Base Distribution
Target Distribution
- Sample
- Evaluate
Siddharth Mishra-Sharma
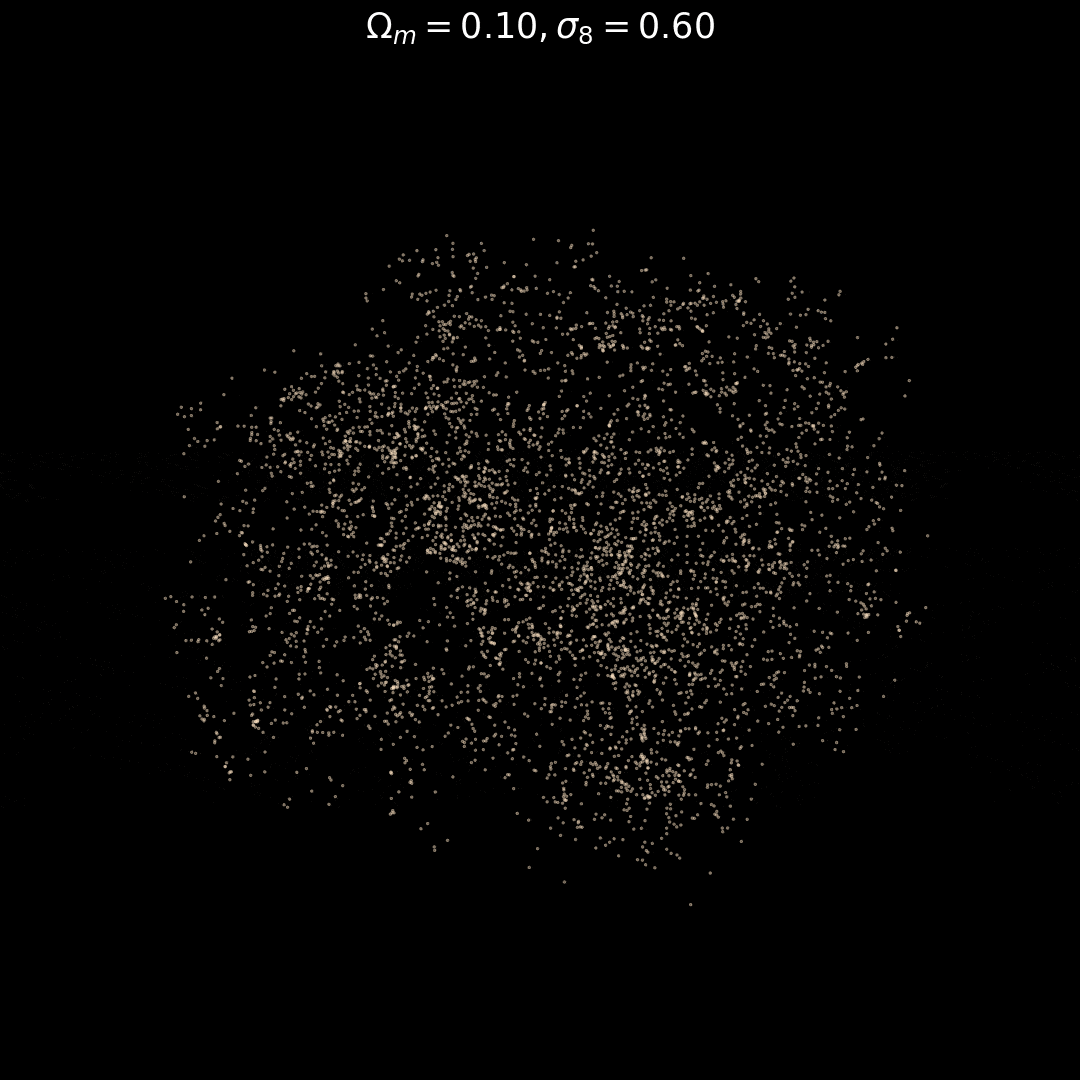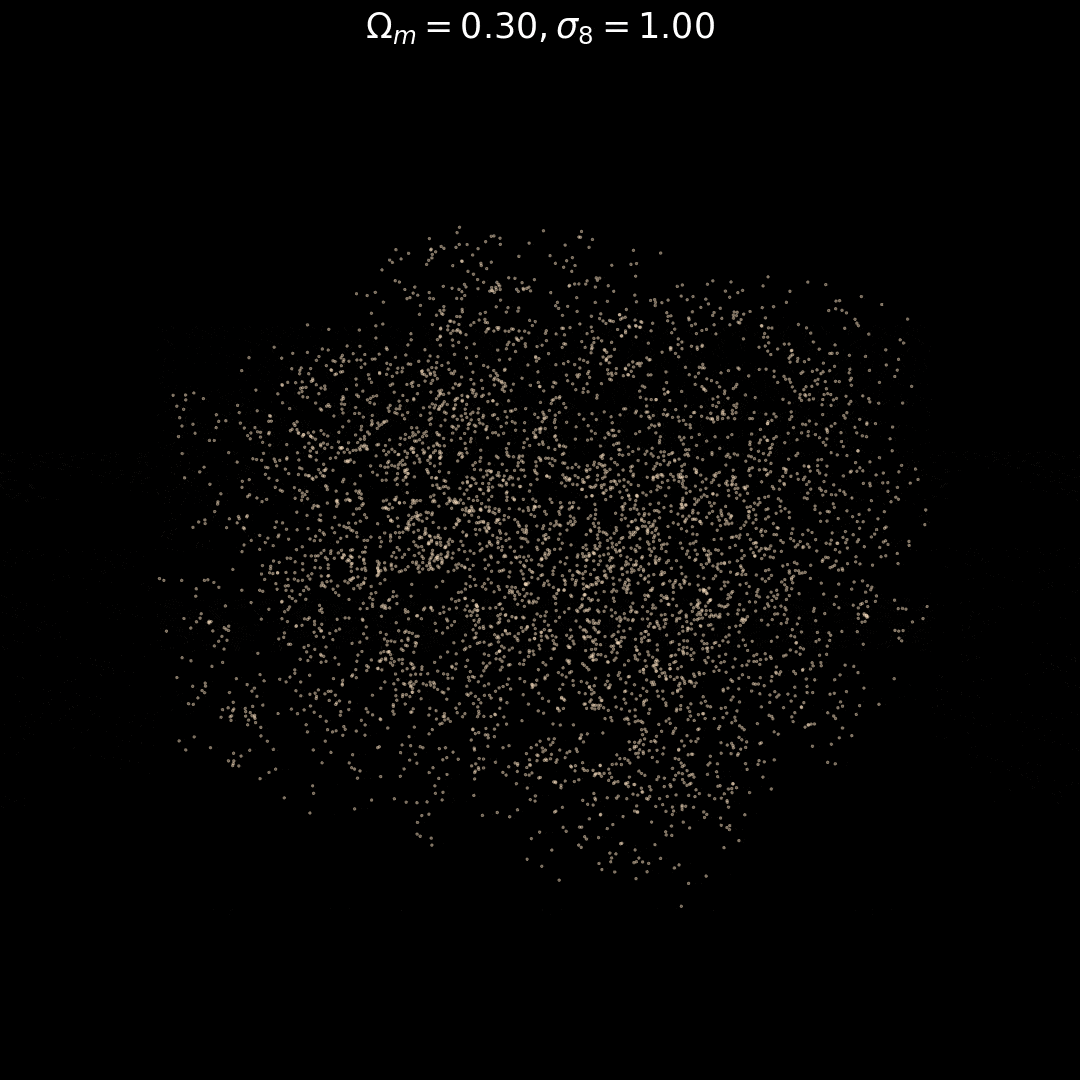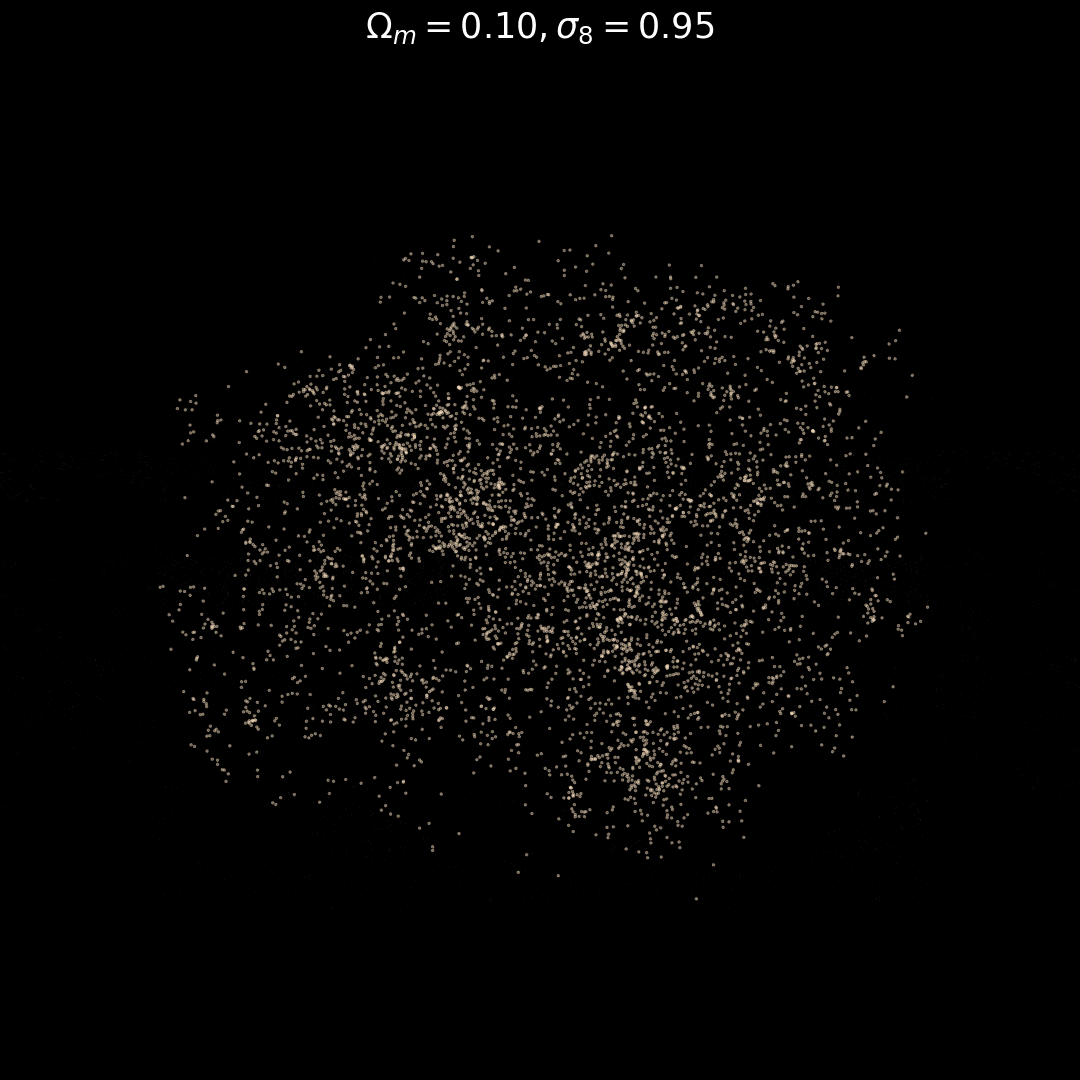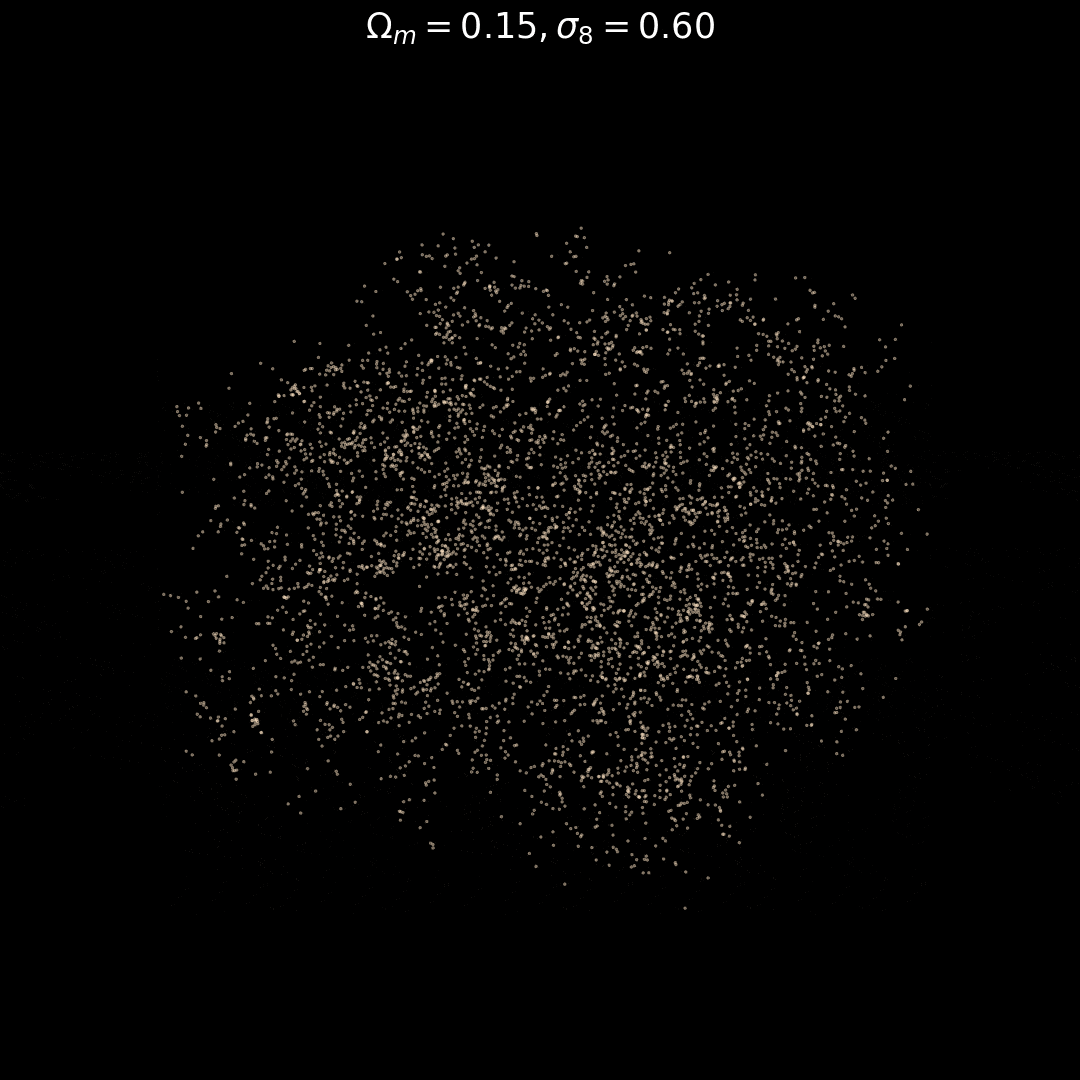
Fixed Initial Conditions
Varying Cosmology
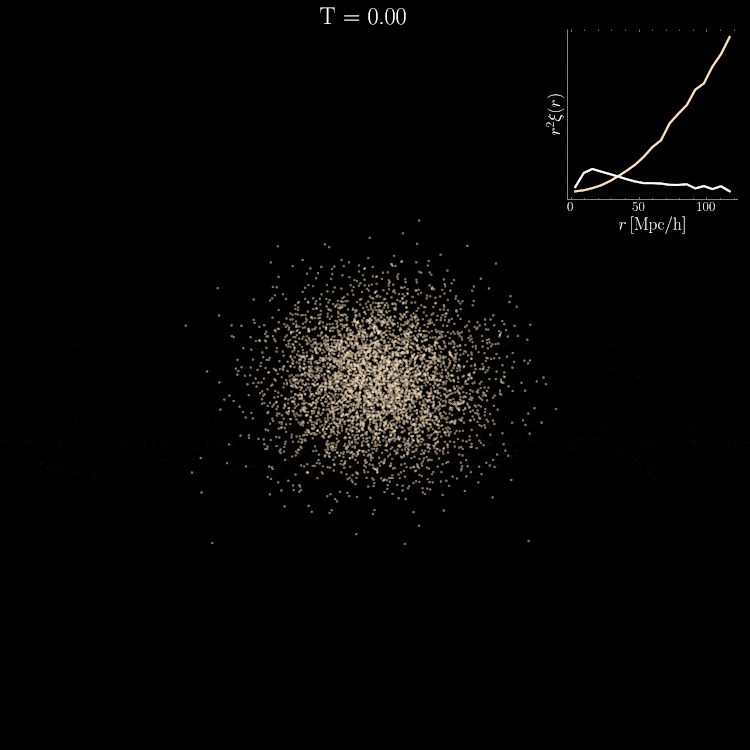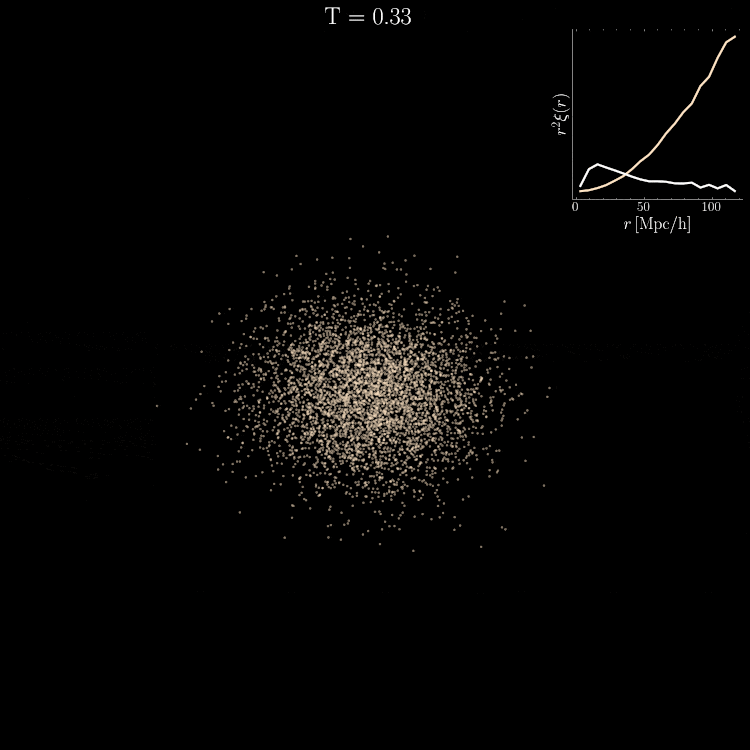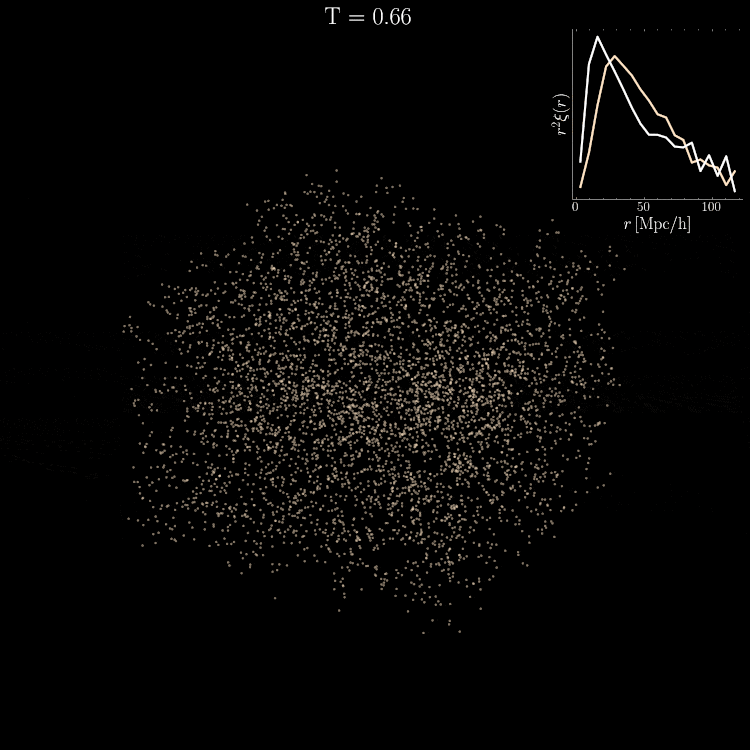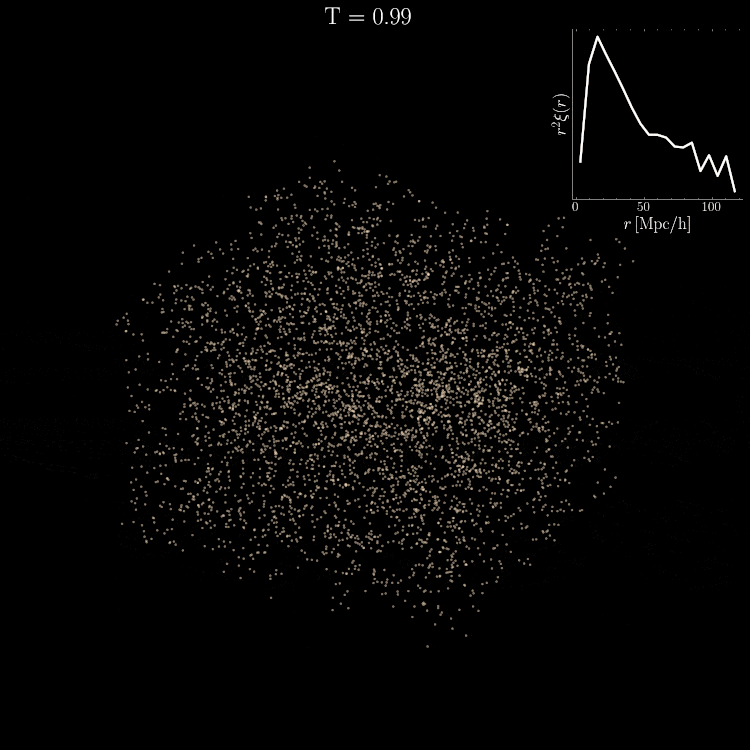
Mean pairwise
velocity
k Nearest neighbours
Pair separation
Pair separation
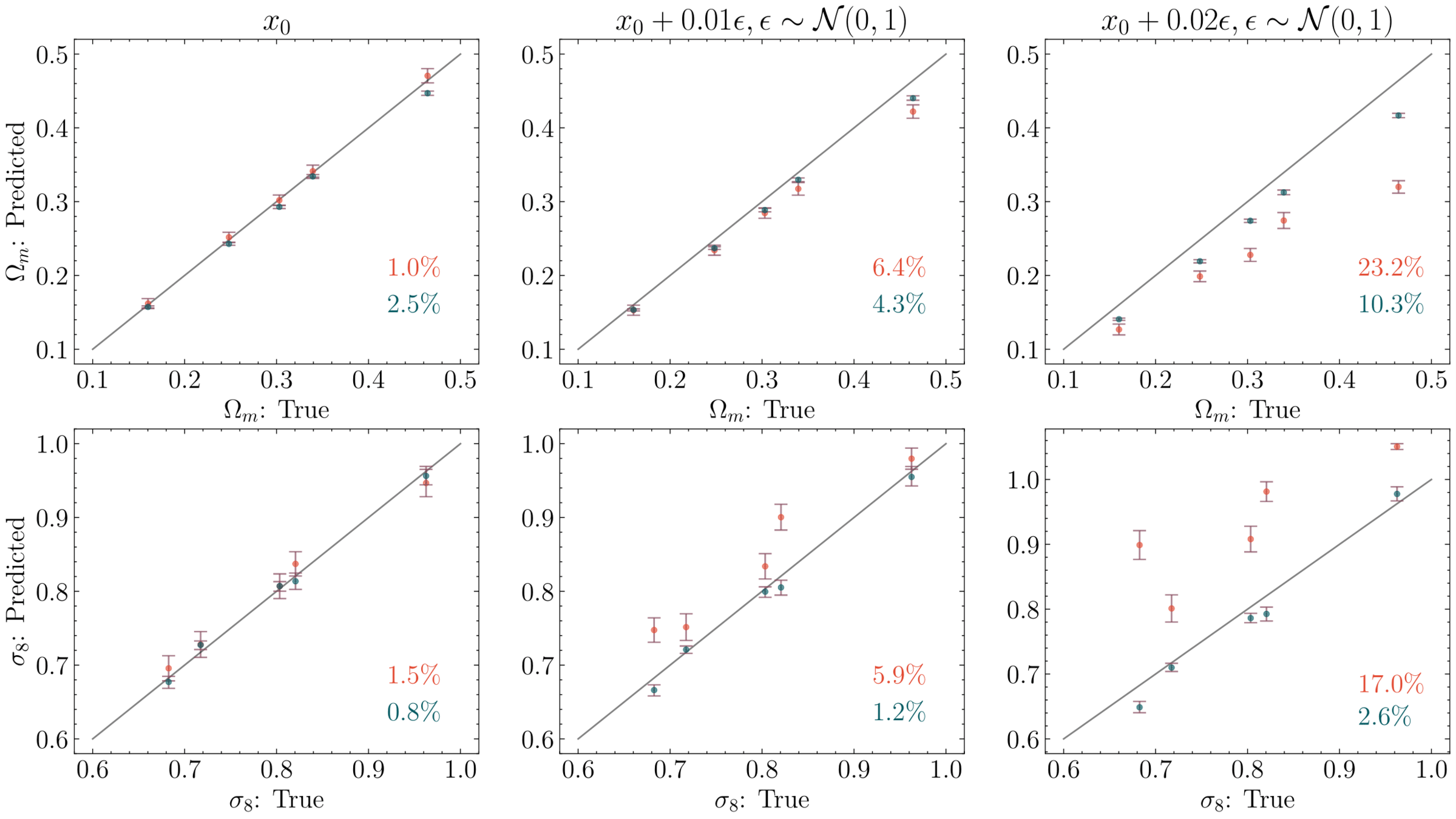
Trained on only 5000 positions!
Learning in 5000 dimensions with only 2000 simulations
Nayantara Mudur
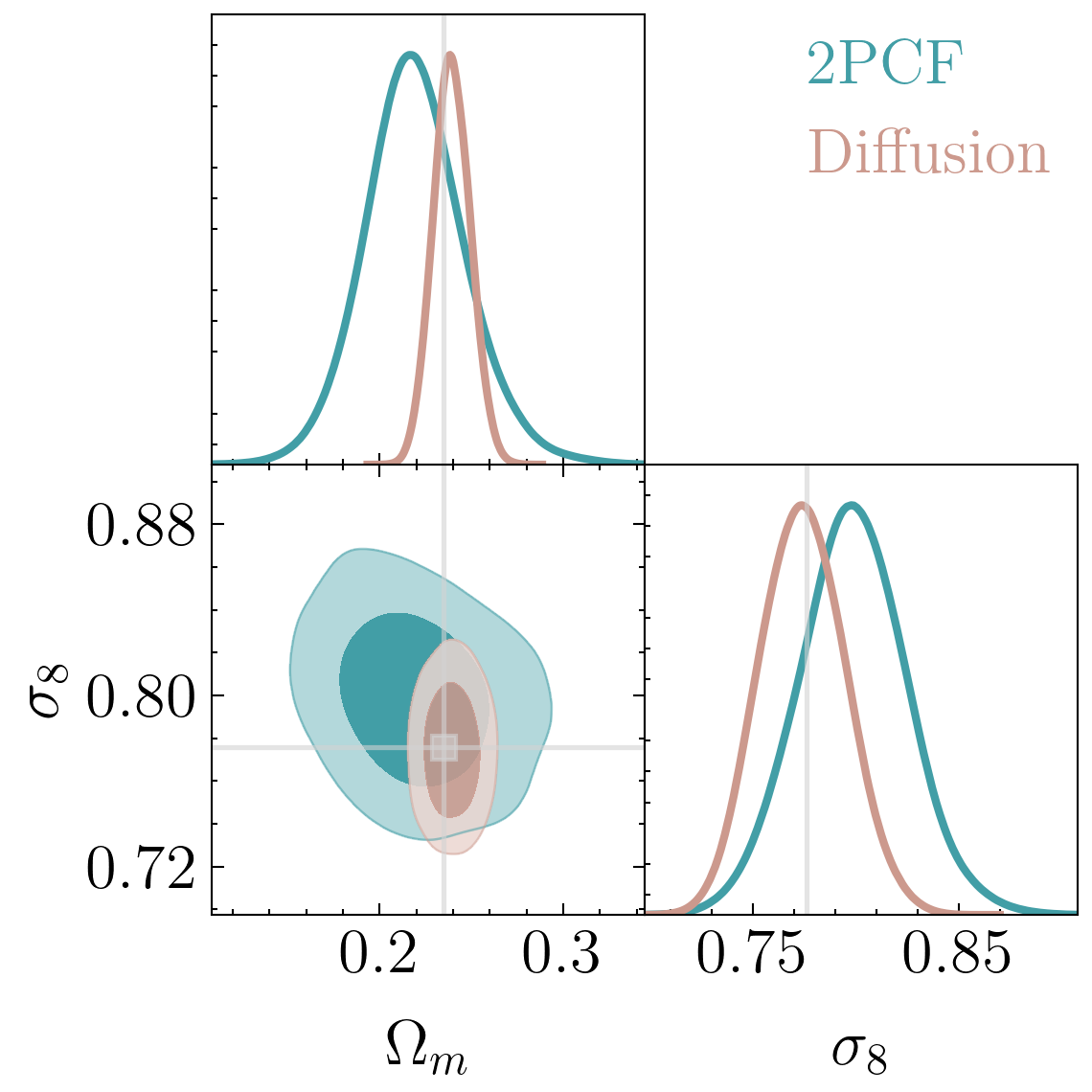
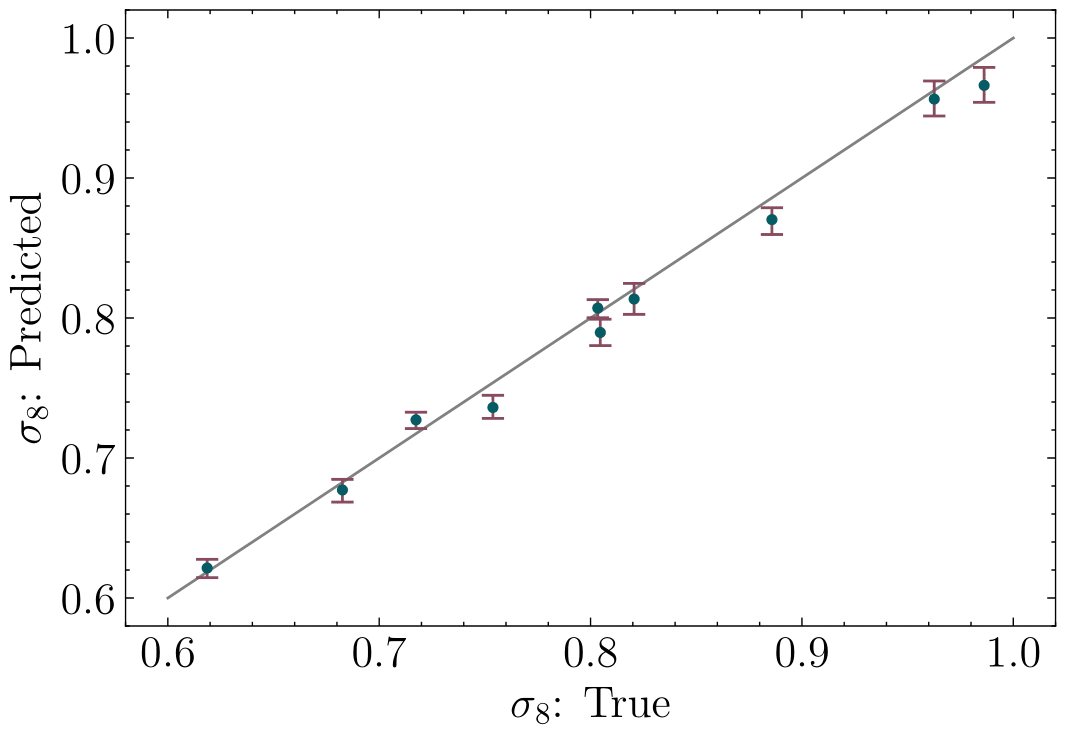
"Diffusion-HMC: Parameter Inference with Diffusion Model driven Hamiltonian Monte Carlo"
Mudur, Cuesta-Lazaro and Finkbeiner
in prep
p(\delta_m|\Omega_m, \sigma_8)
CNN
Diffusion
Increasing Noise
p(\sigma_8|\delta_m)
p(\sigma_8|\delta_m + 0.01 \epsilon)
p(\sigma_8|\delta_m + 0.02 \epsilon)
"Your diffusion model is secretly a certifiably robust classifier"
Chen et al
arXiv:2402.02316
p_\phi(\delta_\mathrm{z=127}|\delta_\mathrm{z=0})
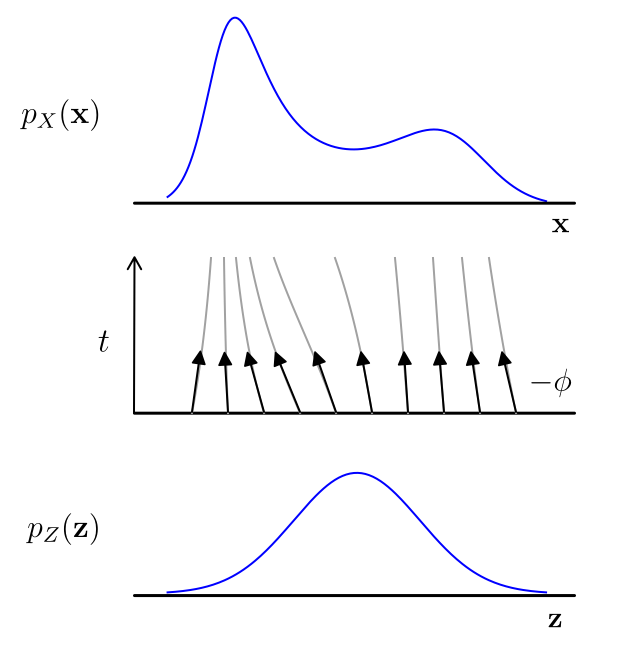
1 to Many:
1 \mathrm{Gpc}/h
https://arxiv.org/abs/2210.02747https://arxiv.org/abs/2302.00482Stochastic Interpolants: Bridging arbitrary densities
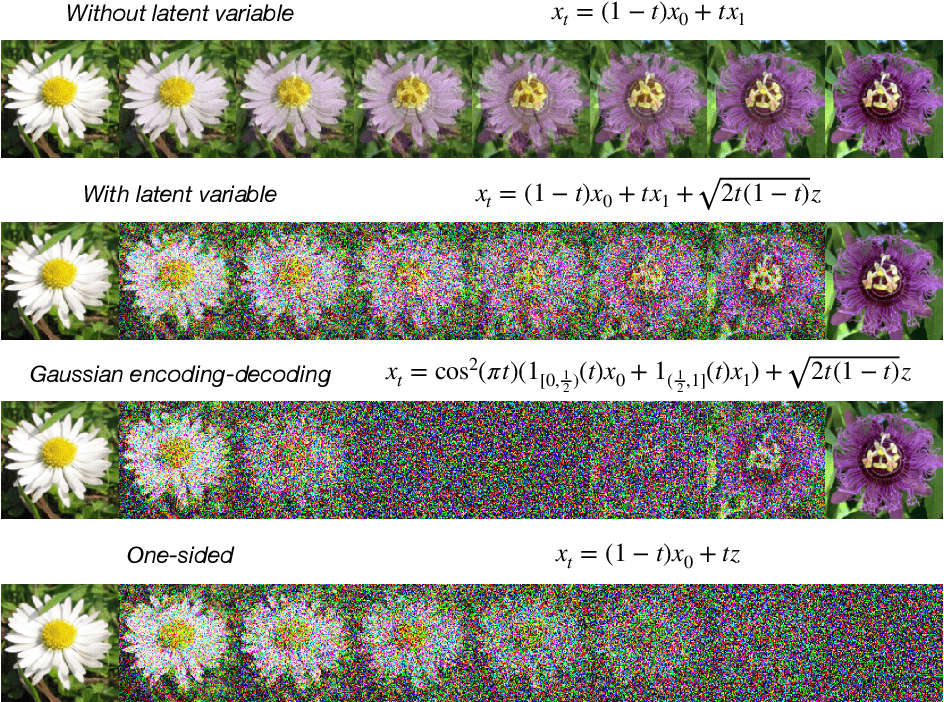
"Stochastic Interpolants: A Unifying Framework for Flows and Diffusions"
Albergo, Boffi, Vanden-Eijnden
arXiv:2303.08797
x_1
x_0
\frac{d x_t}{dt} = u_t(x_t)
Flow ODE
x_0
p(x_0)
p(x_1)
x_1
u_t
\frac{d p_t}{dt} = - \left(\nabla u_t p_t \right)(x_t)
Continuity Equation
Regress the velocity field
L_\mathrm{FM} = \mathrm{min} \, \mathbb{E}_{t, p_t(x|x_0)} \left |\left| v^\theta_t(x|x_0) - u_t(x|x_0) \right|\right|^2
Unknown!
x_t = (1 - t) x_0 + t x_1
p_t(x|x_0)
p_0(x|x_0) = \delta_{x_0}
p_1(x|x_0) = p
Boundary Conditions
https://arxiv.org/abs/2210.02747https://arxiv.org/abs/2302.00482Stochastic Interpolants: Bridging arbitrary densities
"Stochastic Interpolants: A Unifying Framework for Flows and Diffusions"
Albergo, Boffi, Vanden-Eijnden
arXiv:2303.08797
x_t = (1 - t) x_0 + t z
x_0
x_1
x_t = (1 - t) x_0 + t x_1
x_t = (1 - t) x_0 + t x_1 + \sqrt{2t (1-t)z}
Power Spectrum
Cross correlation
Small
Large
Scale (k)
Small
Large
Scale (k)
Small
Large
Scale (k)
Small
Large
Scale (k)
Can we run larger simulations? (DESI volumes)
At high resolution?
Faster?
All this works depends on simulations, but...
Thousands of them?
Hybrid Physical / ML simulators
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})
Gravitational evolution ODE
Particle-mesh
"Nbodyify: Adaptive mesh corrections for PM simulations" Cuesta-Lazaro, Modi in preps
Particle-mesh
Full Nbody
\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]
Hybrid Simulator - on the fly
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
Gravitational evolution ODE
Trained to match particle velocities and positions: DIFFERENTIABLE
\mathcal{L} = \sum_t \left(x_t^{\rm pred} - x_t^{\rm HR}\right)^2
\delta_\mathrm{LR}
\phi_\mathrm{LR}
Density
Gravitational Potential
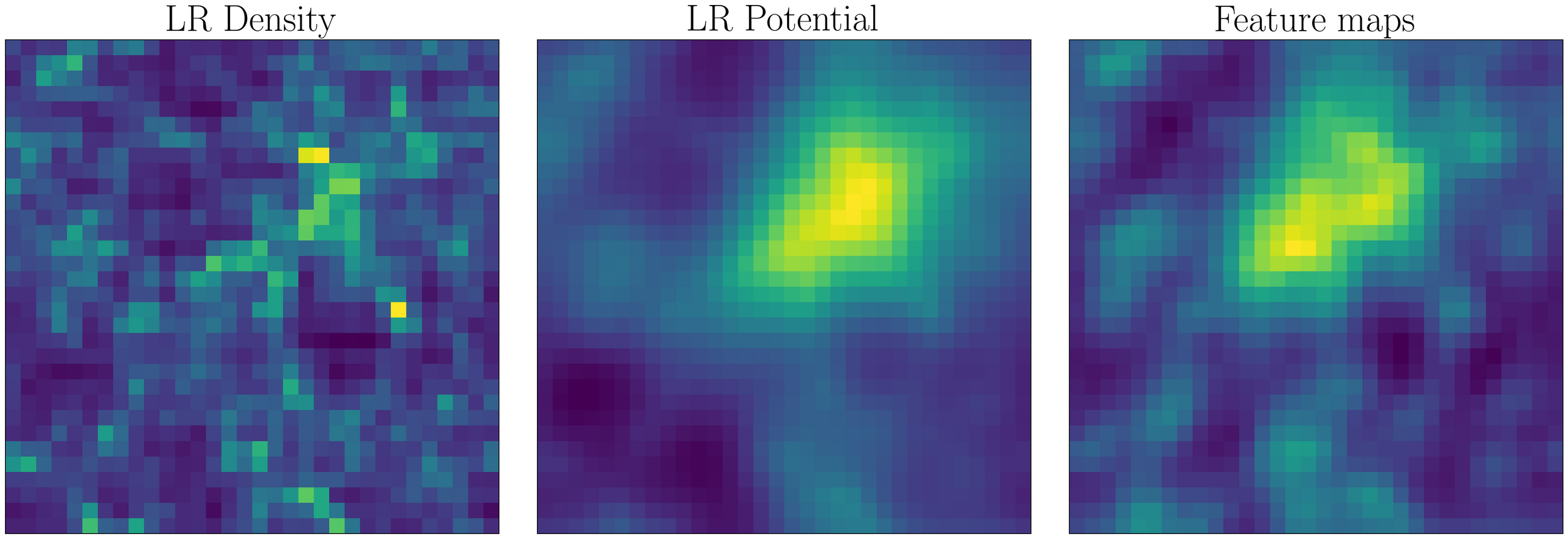
1. CNN
2. Read features at position using attention
\mathbf{F}_\theta(\mathbf{x},a) = f_\theta(h_\theta(\mathbf{x}), a)
3. Compute force correction
4. Run corrected simulation
Learn features
h_\theta(\mathbf{x})
h
Particle-mesh
Full Nbody
Hybrid ML-Simulator
"Nbodyify: Adaptive mesh corrections for PM simulations" Cuesta-Lazaro, Modi in preps
Gravitational potential
Particle velocities
~ Gpc
pc
kpc
Mpc
Gpc
Video credit: Francisco Villaescusa-Navarro
Gas density
Gas temperature
Are there problems in cosmology that bypass a forward model?
Parity violation cannot be originated by gravity
7 \sigma
x
\mathrm{Mirror}(x)
"Measurements of parity-odd modes in the large-scale 4-point function of SDSS..." Hou, Slepian, Chan arXiv:2206.03625
?
1 \sigma
"Could sample variance be responsible for the parity-violating signal seen in the BOSS galaxy survey?" Philcox, Ereza arXiv:2401.09523
x
\mathrm{Mirror}(x)
\mathrm{max} \, \left( f_\theta(x) - f_\theta(\mathrm{Mirror}(x)) \right)
Matthew Craigie
Peter Taylor
Yuan-Sen Ting
Pre-defined filters
No symmetries
Learned filters + symmetries
Reduce the problem to the space of odd-parity functions with equivariant graph networks?
Train
Test
Me: I can't wait to work with observations
Me working with observations:
Conclusions
1. There is a lot of information in galaxy surveys that ML methods can access
2. We can tackle high dimensional inference problems so far unatainable
3. Our ability to simulate will limit the amount of information we can extract
Hybrid simulators, forward models, robustness
Unsupervised problems: parity violation
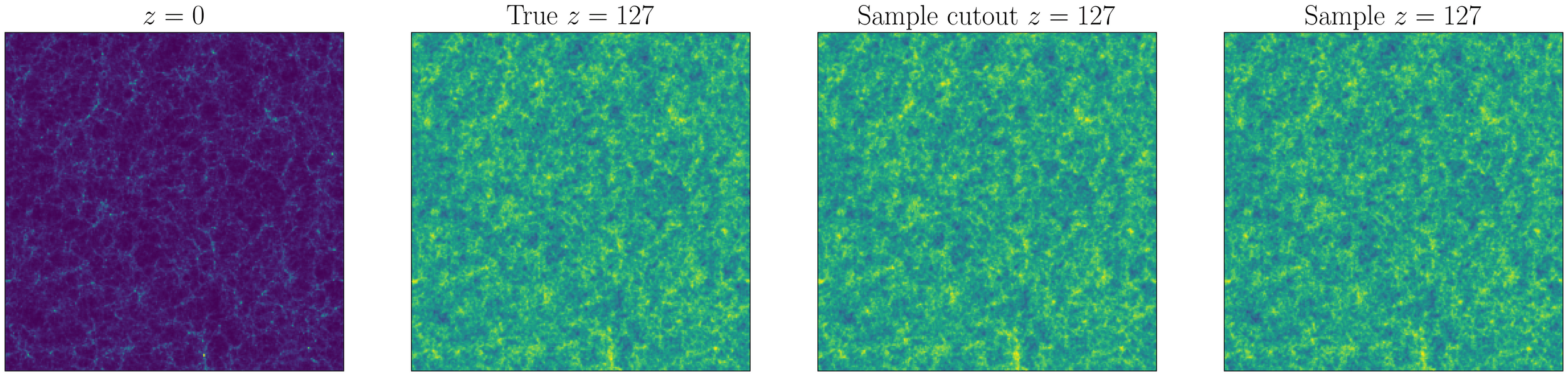
Dark matter density reconstruction, Initial Conditions, let's get creative!
Field level inference
CTPSeminar2024
By carol cuesta
