
Hybrid simulators for cosmology
Carol Cuesta-Lazaro and Chirag Modi
IAIFI Fellow - AstroAI
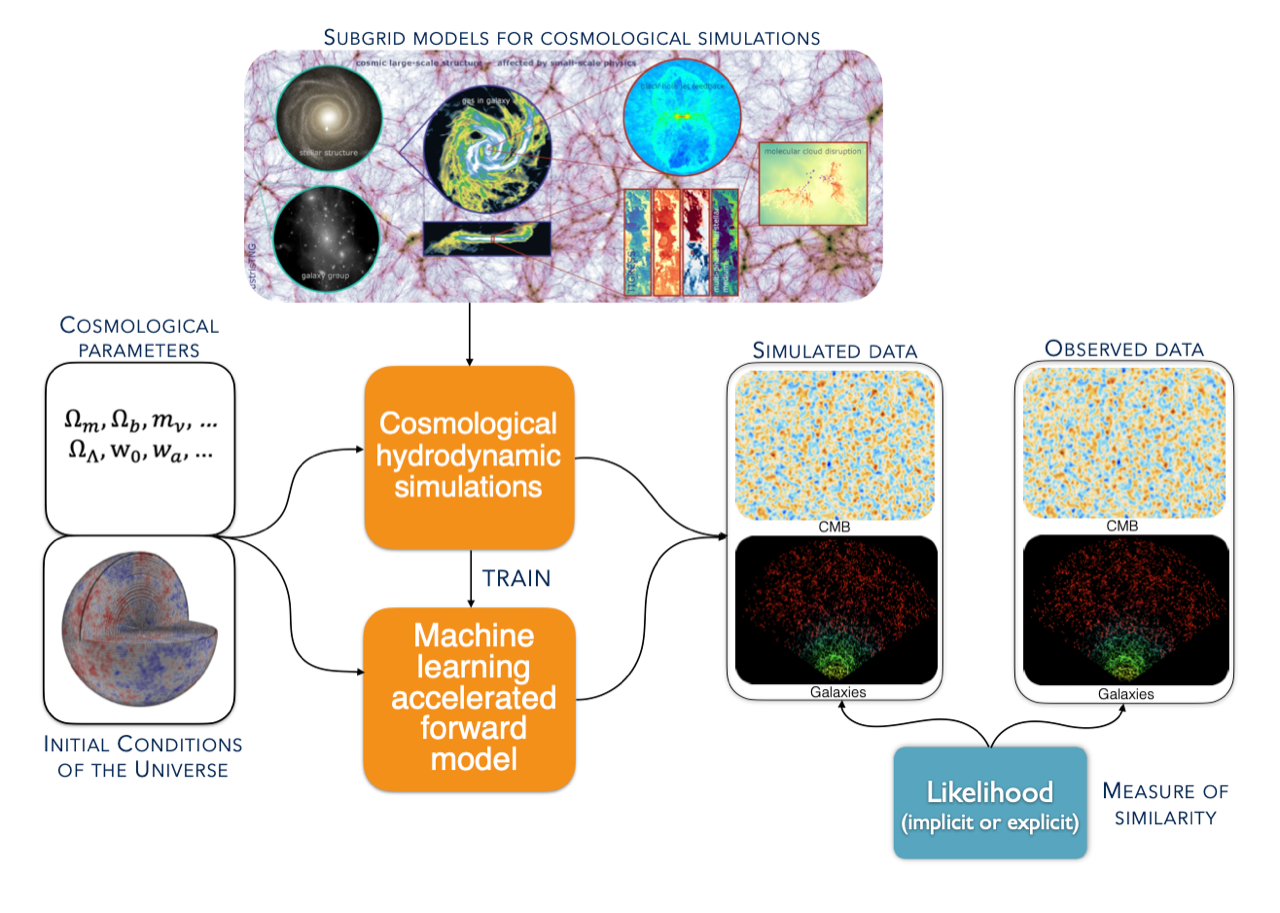

Learning The Universe (LtU)

TNG50
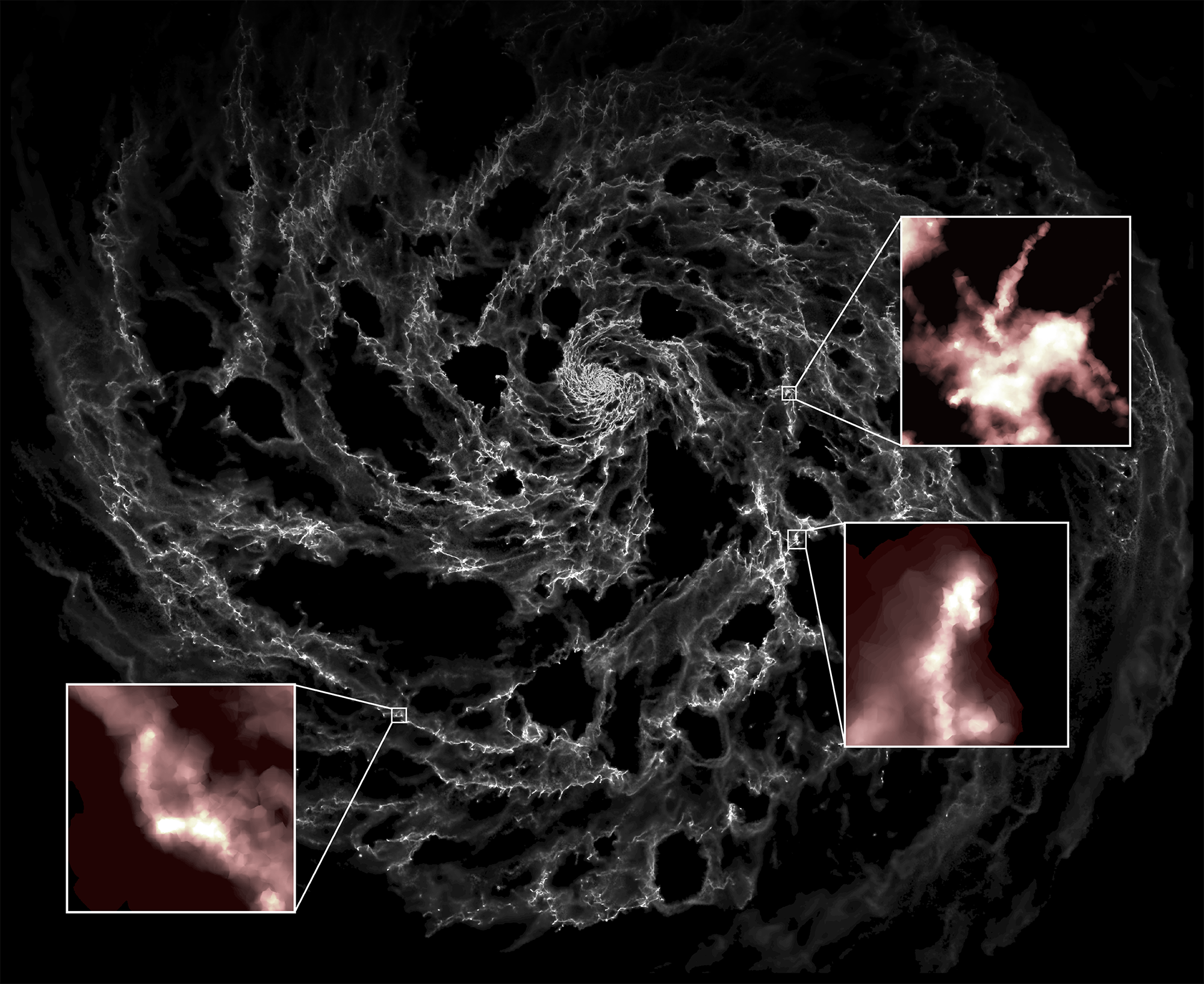
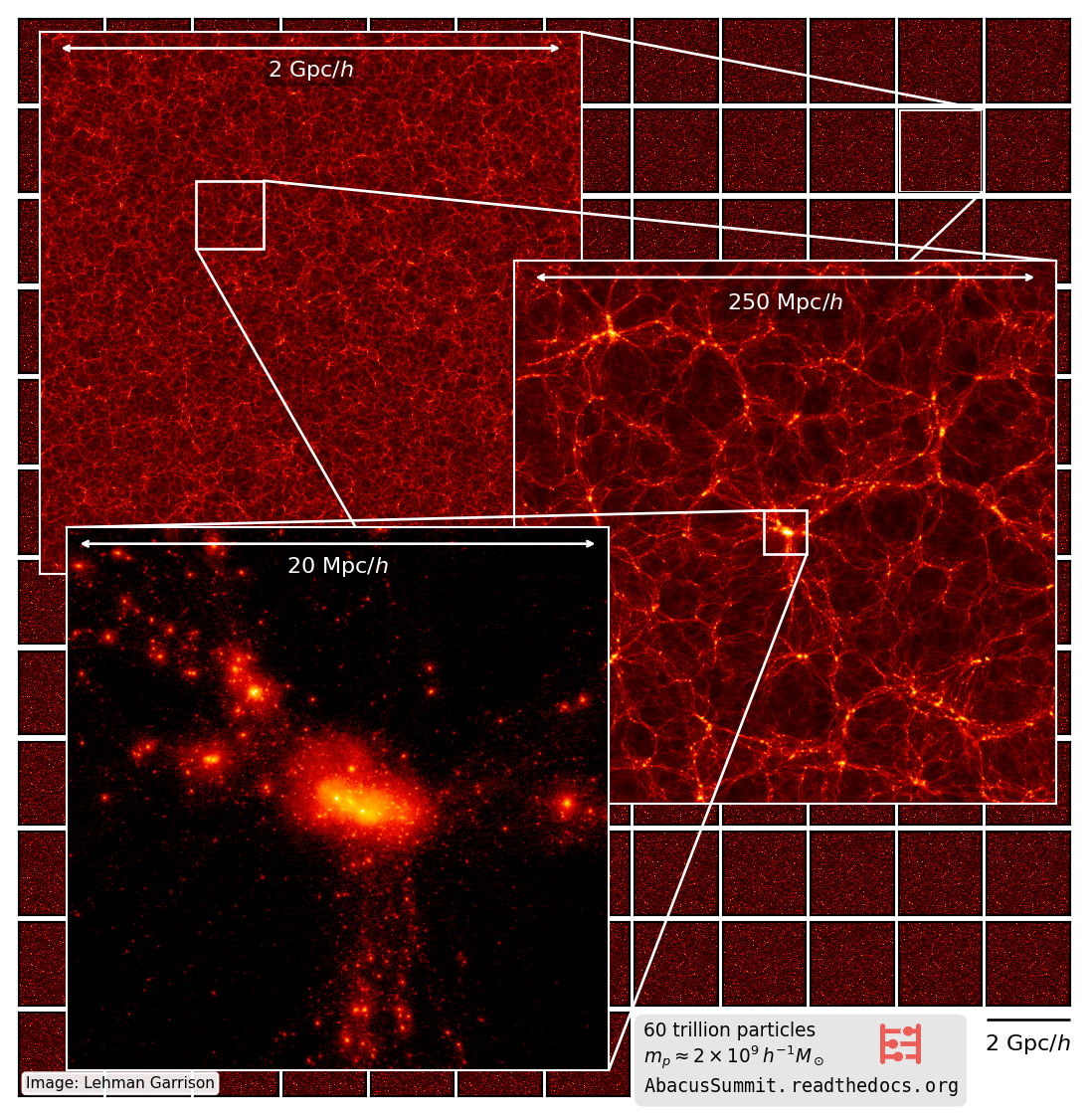
Image credit: Sarah JeffresonImage credit: Lehman Garrison, AbacusSummit\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
Physics Simulator
x_{\rm Initial}
x_{\rm Final}
Neural Network
x_{\rm Initial}
x_{\rm Final}

Hybrid Model
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a) +

x_{\rm Initial}
x_{\rm Final}

Nbody
Slow
Non-differentiable
Particle mesh
Accurate
Fast
Differentiable
Missing small scales
Nbodyify
Fast
Differentiable
Accurate



"Nbodyify: adaptive mesh corrections for PM simulations" Carolina Cuesta-Lazaro, Chirag Modi (in prep)
\frac{\mathrm{d} \mathbf{x}}{\mathrm{d} a } = \frac{1}{a^3 E(a)}\mathbf{v}
\frac{\mathrm{d} \mathbf{v}}{\mathrm{d} a } = \frac{1}{a^2 E(a)}\mathbf{F}(\mathbf{x},a)
\mathbf{F}_\theta(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \left[\phi^\mathrm{PM}(\mathbf{x}) + \phi^\mathrm{corr}_\theta(\mathbf{x}, a, \phi^\mathrm{PM}, \delta^\mathrm{PM}) \right]
\mathbf{F}(\mathbf{x},a) = \frac{3 \Omega_m}{2} \nabla \phi^\mathrm{PM}(\mathbf{x})
Gravitational evolution ODE
Particle-mesh
Hybrid Simulator
\mathcal{L} = \sum_t \left(x_t^{\rm pred} - x_t^{\rm HR}\right)^2


\delta_\mathrm{LR}
\phi_\mathrm{LR}
Density
Gravitational Potential
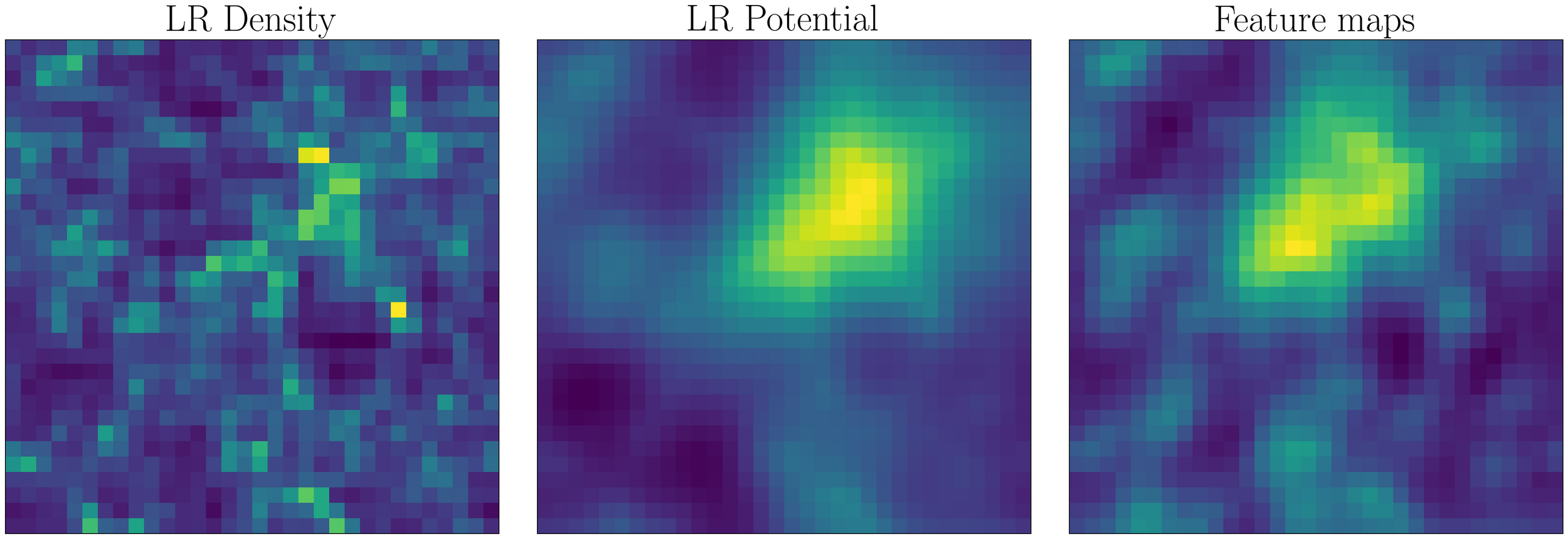
1. CNN
2. Read features at position using attention
h_\theta(\mathbf{x})
\mathbf{F}_\theta(\mathbf{x},a) = f_\theta(h_\theta(\mathbf{x}), a)
3. Compute correction to force
4. Run corrected simulation

d_{\rm pm}
W_{\rm m} = f_\theta(d_{\rm pm}, h_{\rm m})
h(x) = \sum_m w_{\rm m} h_{\rm m}









Power Spectrum
Cross correlation

Power Spectrum
Cross correlation


Improving small scales?

p(x_{\rm LR}|x_{\rm HR})
Do we need particle-particle interactions?
Turn probabilistic!
deck
By carol cuesta
deck
- 593



