DP & Game Theory
DP 不是教過了嗎?
某張姓學長表示:「我連兩場模競出DP都滅台耶」
來說說你所認知的 DP 吧
BTW 他好嗆www
來看看題目吧
營地
給定 \(N*M\) (\(N, M \leq 5000\)) 的二維陣列,求最大不包含 2 的正方形面積
艾迪摺紙趣
給定 \(N*M\) (\(N, M \leq 100\)) 的矩形,問至少要用幾個正方形來拼湊
最大不連續和
給一個長度為 \(N\) (\(N\leq 10^6\)) 的序列
求其最大不連續子序列的和
撿石子遊戲
給一個長度為 \(N\) (\(N\leq 2*10^6\)) 的且只包含 'P', 'E', 'C' 三個字元的字串,任選三個不相交的區間P, E, C
求【P中'P'的數量+E中'E'的數量+C中'C'的數量】最大值
最大二維子矩陣
給一個 \(N*M\) 的二維陣列,請輸出最大可能的子矩陣總和
期望能達到的複雜度: \(O(N^3)\) (\(N, M\) 視為相同數量級)
應該知道 \(N^4\) 的作法(?
可以想想要怎麼用一維最大子矩陣來協助
倍因道
\(1\)~\(N\) 的整數中,你可以將一些數字歸類為「因數」,另一些則歸類為「倍數」,對於每個「倍數」可以得到的分數就是他有多少個因數被歸類為「因數」,求最大可能達到的總分
每個數字如果放在「因數」或「倍數」分別會得到多少分(?
嚴格遞增子序列計數
給你一個長度為 \(N\) (\(N \leq 10^5\)) 的序列,求有多少個長度 \(\leq K\) (\(K \leq 70\)) 的嚴格遞增子序列
你可能會需要一些區間資料結構的協助
數列切割
給定一個長度為 \(N\) (\(N \leq 10^6\)) 的序列,你可以將序列切成 \(K\) (\(K \leq 6\)) 份,求一種切法使得【偶數份的和 - 奇數份的和】最大
記得要維護轉移來源!
有限背包
重量上限 \(T\) 的背包,有 \(N\) 種物品,每種物品有價值 \(V\)、重量 \(W\),且共有 \(C\) 個
\(N, T\leq 10^6\) 且 \(NT\leq 10^7\)
\(V, W, C\leq 10^3\)
直接轉成 01背包的話物品似乎有點太多了(?
有沒有辦法用更好的方法表達 \(n\) 件相同的物品?
\(O(N)\) 算法就交給下學期dp優化講師吧><
打地鼠
給定 \(N\) (\(N \leq 16\)) 個地鼠洞,編號為 \(i\) 的地鼠每 \(T_i\) 秒會出現一次,玩家以每秒一格的速度移動(打地鼠的時間忽略不計)
請問至少需要多久才能打完所有地鼠請問至少需要多少時間才能打完所有地鼠?
如果我們知道打掉任意 \(n-1\) 個地鼠的答案,有沒有辦法快速算出答案?
要怎麼紀錄打掉了任意幾隻地鼠的答案?
位元dp
以一個 bitset 來記錄狀態
一個 bitset 狀態 \(i\) 表示打掉地鼠的集合
一個狀態 \(j\) 表示得到這個集合時最後在哪個位置
\(\displaystyle dp[i][j] = \min_{\forall 2^k \land i, 0 \leq k < n}\{dp[i][j], \lceil \frac{dp[i\oplus 2^j][k] + dis(j, k)}{T[j]}\rceil \cdot T[j] \}\)
\(\displaystyle \min_{0 \leq k < n}\{dp[2^n-1][j]\}\) 即為所求
跳格子遊戲
給你一個 DAG (\(V\leq 10^4, E\leq 10^5\))以及起點和終點,有兩個人在玩遊戲,一開始由一人在起點,兩個人輪流選擇走到另一個人所在的點連到的任意點,到達終點的人就贏了,求先手還是後手有必勝策略
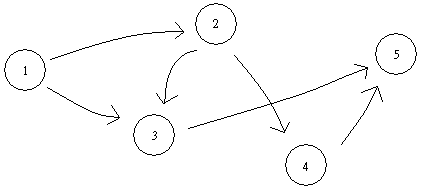
走到任何一個連到終點的點就輸了
耶!賽局
預判勝負
用 \(0, 1\) 來代表兩個玩家,定義轉移函數 \(F\) 和勝負函數 \(S\)
對於一個輪到 \(a\) 動的盤面 \(x\),
\(F(x, a) = \{y | a \text{ 可以將狀態 } x \text{ 轉移到狀態 } y \}\)
\(S(x, a)\) 為 \(1\) 代表 \(a\) 會贏、 \(0\) 代表平手、 \(-1\) 則是 \(a\) 會輸
我們可以得到 \(S(x, a) = - \min\limits_{y \in F(x, a)} S(y, 1-a)\)
對稱遊戲
\(\forall x \{F(x, 0) = F(x, 1) \text{ and } S(x, 0) = S(x, 1)\}\)
組合賽局
- 兩位玩家對戰,雙方輪流操作
- 資訊完全公開
- 沒有任何機率因素
- 遊戲會在有限步內結束
三一遊戲
有 \(N\) 顆石頭,每次可以拿 \(1\)~\(3\) 顆,兩個人輪流拿,拿到最後一顆的人贏,求誰有必勝策略
有 \(N\) 堆石頭 (\(N\) 是偶數),每次選擇 \(N/2\) 堆石頭分別拿正整數顆 (每堆可以拿不一樣多),兩個人輪流拿,拿到剩下石頭堆數少於 \(N/2\) 時就輸了,求誰有必勝策略
Thanos nim
Nim
有 \(N\) 堆石頭,每次堆有 \(a_i\) 顆,每次可以選擇任意一堆拿 \(1\) ~ \(N\) 顆,兩個人輪流拿,拿到不能拿的就輸了,求誰有必勝策略
在討論這題之前...
\(SG\)值
對於一個狀態 \(x\) ,定義其 \(SG\)值為其可以透過一次操作走到的狀態的 \(SG\)值中,最小未出現的非負整數
後手必勝若且唯若 \(SG(x) = 0\)
\(mex\) 函數
定義 \(Mex\) 函數為一個非負整數集合中最小未出現的非負整數
Sprague-grundy theorem
\(SG(x_1+x_2) = SG(x_1) \oplus SG(x_2)\)
由定義可知:
\(SG(y) \neq SG(x), \forall y \in F(x)\)
定義 \(G(x_1+x_2) = SG(x_1) \oplus SG(x_2)\)
在新遊戲 \(x_1+x_2\) 中,假設把 \(x_1\) 走到 \(y\):
則 \(G(y+x_2) \neq SG(x_1) \oplus SG(x_2)\)
還需要證明:
\(x_1+x_2\) 可以走到任何小於 \( SG(x_1) \oplus SG(x_2)\) 的狀態
則 \(G(x)\) 才會滿足 \(SG\) 函數的性質
這就留給大家想想看(?
\(SG(x_1+x_2) = SG(x_1) \oplus SG(x_2)\)
每一堆石頭的 \(SG\)值是多少?
整個 NIM 的 \(SG\)值是多少?
如何判斷誰有必勝策略?
必勝策略是什麼?
回到剛剛的 NIM
同 NIM,但多了一個限制條件:
對於任意一堆石頭 \(a_i\),每次拿的石頭顆數不能重複
(\(N \leq 10^6, a_i \leq 60\))
Game of stones
回憶一下這堂課除了 NIM 還教過什麼
有一顆 \(N\) (\(N \leq 10^5\)) 個節點的樹,每個節點分別有 \(a_i\) (\(a_i \leq 10^7\)) 顆蘋果,這顆樹很特別,他的樹根到每個葉子的距離 \(mod 2\) 皆相同
兩個人輪流進行遊戲,每次將任一節點上的 \(x (x > 0)\) 顆蘋果丟給其中一個子節點,若該節點為葉子則直接把蘋果吃掉
先手在開始前可以預先調換兩個節點的蘋果數量,不能動的人算輸,求有幾種調換方法可以讓先手必勝
sagheer & 蘋果樹
可以想想看【樹根到每個葉子的距離 \(mod 2\) 皆相同】這個奇怪的條件是要幹嘛
如果你看到這邊就表示
講師沒題目可以唬爛了QQ
DP & Game Theory
By CasperWang
DP & Game Theory
- 1,226



