Corentin Cadiou
Postdoc @ Lund University
Chargé de recherche CNRS from Feb. @ IAP, Paris


Moving to exa-scale —challenges to (large) cosmological simulations

Mellier+24

Schaye+24
Sims including baryons:
\(\sim 100\times\) smaller volumes than observed
- How to beat cosmic variance?
- How to understand \(k>10\,h\,\mathrm{Mpc}^{-1}\) effects?
Part I:
(somewhat) clever solutions
Genetic Modification Method (GM)
There's a lot of freedom in the initial conditions.
\(\tilde\delta=\sum_k {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_\mathrm{k}})\)
Constraint:
\(\langle a_{\mathbf{k}} a_{\mathbf{k'}}^\dagger\rangle = P(k)\delta_\mathrm{D}(\mathbf{k}-\mathbf{k}')\)
Constraint:
\(\phi_\mathrm{k}\sim \mathcal{U}(0,2\pi)\)
a. Inverted Initial Conditions
Utilizing inverted initial conditions to enhance estimators accuracy.
Pontzen+15, see also Chartier+21, Gábor+23

\(\tilde\delta_\mathrm{S}=\sum_{k<k_\mathrm{thr}} {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_k})+\sum_{k>k_\mathrm{thr}} {\color{green} a_k} \exp(i\mathbf{k r} + {\color{red}\phi_k+\pi})\)

\( 3^{\mathrm{rd}}\)-order correction
/ up-to-\(2^{\mathrm{nd}}\)
b. Splicing Technique
Most likely field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))
Mathematically, \({\color{green}f}\) is the unique solution that satisfies:
- \( {\color{green}f(x)}= {\color{blue}a(x)},\qquad\qquad\qquad\forall x \in\Gamma\)
- minimizes \[\mathcal{Q} = ({\color{red}b}-{\color{green}f})^\dagger\mathbf{C}^{-1}({\color{red}b}-{\color{green}f}),\quad \forall x \not\in \Gamma \]
CC+21a





b. Splicing Technique

Same halo, different location in the cosmic web


\(z=0\)
\(z=0\)
\(z=0\)
Storck, CC+24
b. Splicing Technique

Same halo, different location in the cosmic web

Halo mass
Intrinsic
alignment
\(\sigma\)
Storck, CC+24
b. Splicing Technique
Same halo, different location in the cosmic web

\(\sigma\)
⇒ 10-100% of I.A. signal driven by the cosmic web*
*couplings beyond standard predictions, from e.g. constrained TTT
Storck, CC+24

Std. dev / mean
Numerical noise
Population scatter
c. Angular momentum GMO
Same galaxy, different tidal enviroment
CC+21b
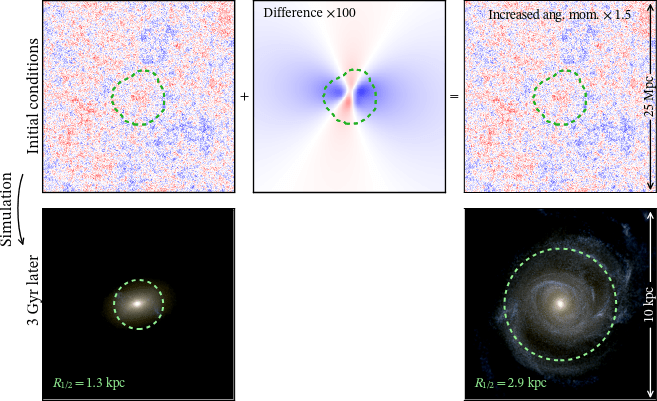
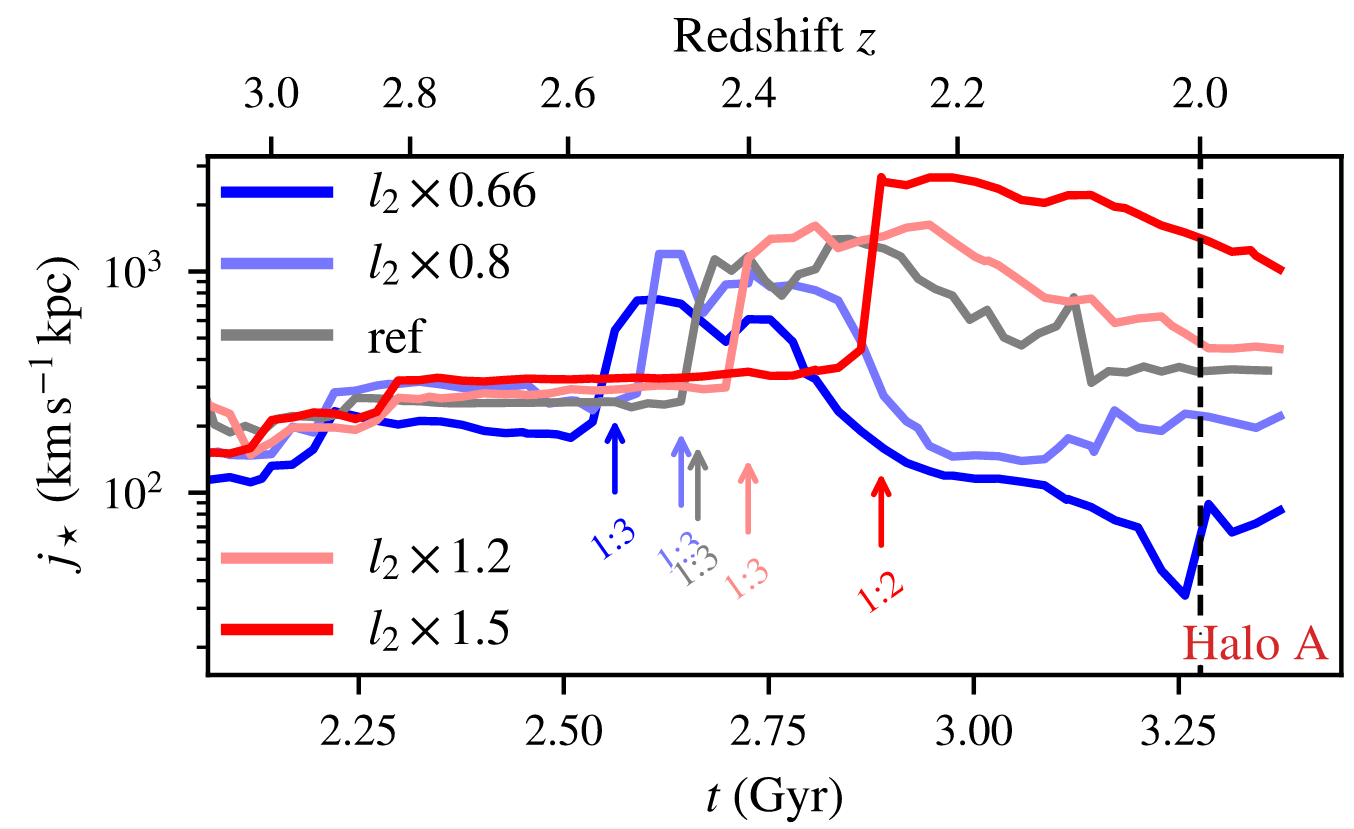
Study response at low-\(z\)
\(k>10\,h\,\mathrm{Mpc}^{-1}\)
Perturb tides at \(z\rightarrow\infty\)
on \(10-100\,h^{-1}\,\mathrm{Mpc}/h\)
LSS perturbations propagate quasi-linearly down to \(\mathrm{kpc}\) scales
⇒ Large \(k\) contain cosmological information
Part II:
bruteforce solutions
“When everything else fails, use more CPU time”
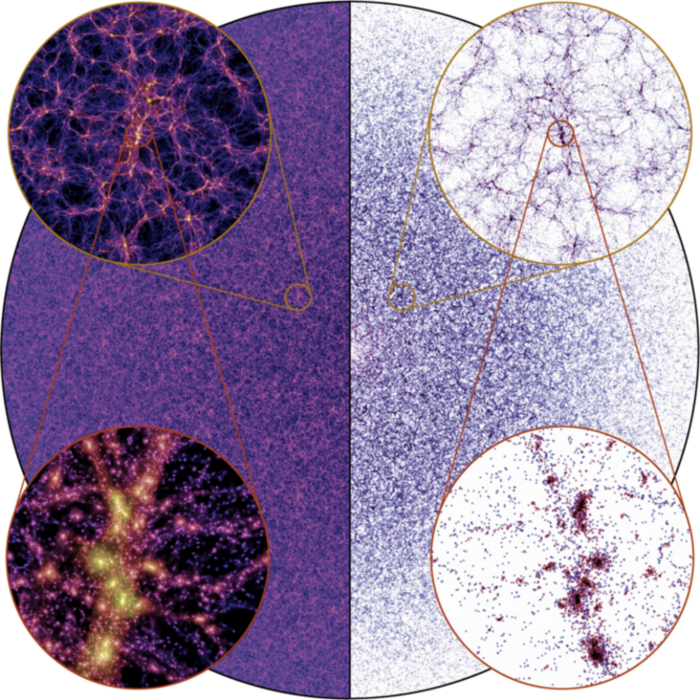
FLAMINGO (Schaye+23)
\(21\,\mathrm{Gpc}^3\), SWIFT
→ SPH approach

Large-volume hydro-cosmo simulations
State-of-the-art
Millenium-TNG (Springel+22)
\(0.125\,\mathrm{Gpc}^3\), Arepo
→ moving-mesh approach
Grid-based code?
Quite a shame, because it's where France's experts are
(Dubois, Hennebelle, Bournaud, …)
?
“When everything else fails, use more CPU time”

Data: Top-500
“When you run out of CPU time, move onto GPUs”

Dyablo Simulation Code
Manage grid, simple computation
Computation-heavy
(hydro, gravity, …)
CPU
GPU
[…]
wasted
time
wasted
time
Typical approach: offloading
Dyablo's approach:
Amdahl's law: latency kills gains of parallelisation
(see F. Leclercq talk)
Dyablo Simulation Code
Manage grid, simple computation
Computation-heavy
(hydro, gravity, …)
CPU
GPU
(or CPUs)
[…]
Typical approach: offloading
Dyablo's approach: “true” GPU computing, CPU as a puppeteer
Main developers: P. Kestener, A. Durocher, M. Delorme (CEA)
+ GINEA collaboration (ObAS, IAP, CRAL, CRIStAL …)
☑ Hydrodynamics
(M. Delorme, A. Durocher)
☑ Gravity
(A. Durocher, M.-A. Breton)
☑ Cosmology
(O. Marchal, D. Aubert)
Today
Spring 2025?
“Full” cosmological sim on GPU
Dyablo: status
☐ Gas cooling (CC)
☐ Star form. & feedback (incl. CC)
+ RT, MHD, testing, setting up ICs, ...



Dyablo: how does it scale?
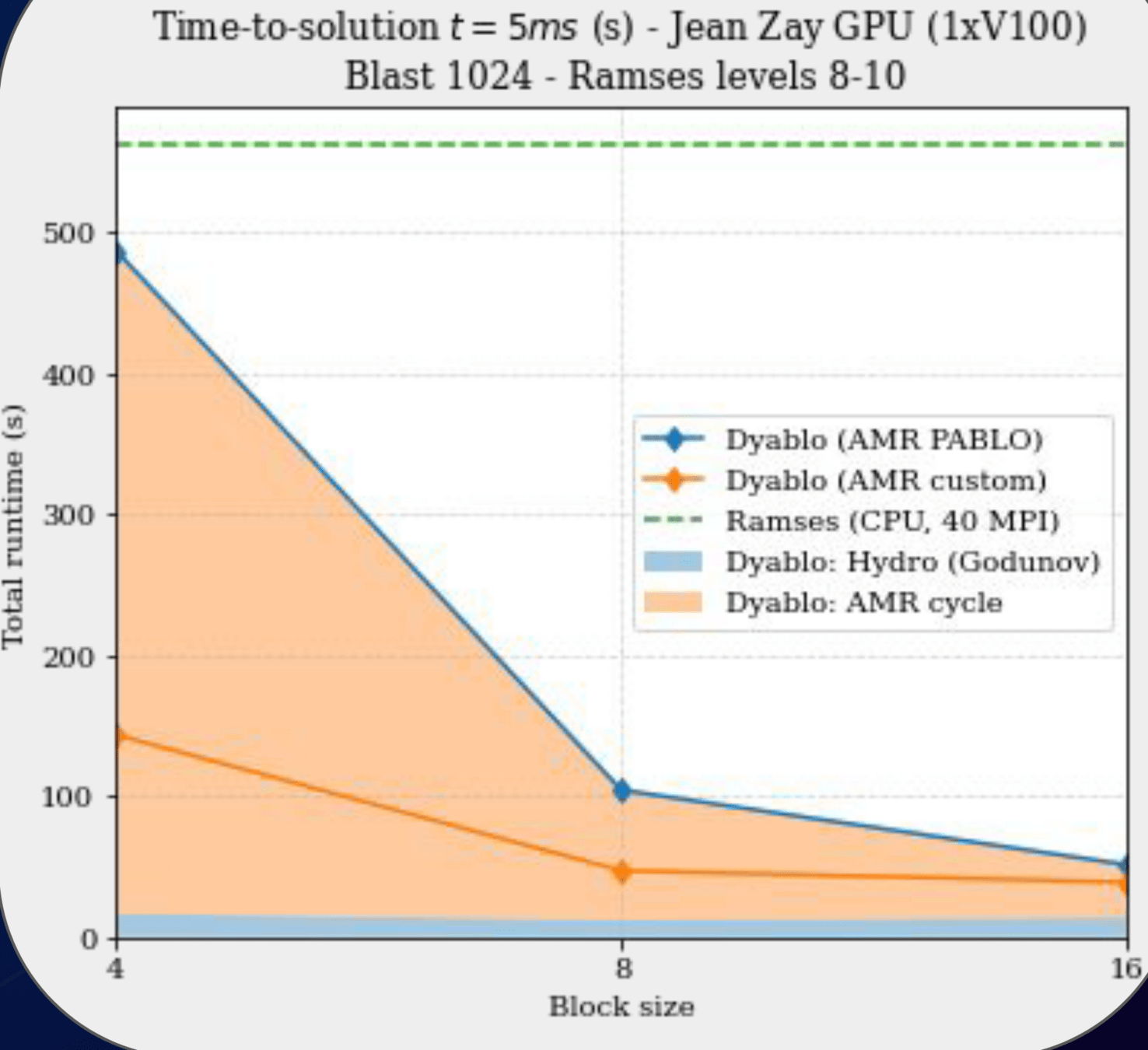

Image credits: Arnaud Durocher
Conclusion & take home message
- Possible to build cosmological experiment
⇒ GMs as machine to study scale couplings- Thoughts on possible applications for DE/DM questions?
- \(10\,\mathrm{Mpc}/h\leftrightarrow \mathrm{kpc}\) for scalars (Mass, \(R_\mathrm{vir}\), ...) is small
-
from \(\sim 100\,\mathrm{Mpc}/h\) to \(\sim \mathrm{kpc}\) large for vector quantities (AM, shape)
- When clever approaches fail, resort to brute force
- Future is (most likely) driven by GPUs
- Promising developments in France with Dyablo
https://github.com/Dyablo-HPC/Dyablo
Moving to exa-scale - challenges to (large) cosmological simulations
By Corentin Cadiou
Moving to exa-scale - challenges to (large) cosmological simulations
- 301



