貪婪演算法
Greedy Algorithm
林芊妘
常見演算法
分治法
貪婪法
動態規劃
回溯法
分支定界法
✔
✔

週四的演算法放課會教喔
分治法-n階層
Divide and Conquer
分治法:將問題拆分為獨立子問題,遞迴求解後合併
9!=9x8x7x6x5x4x3x2x1
8!=8x7x6x5x4x3x2x1
7!=7x6x5x4x3x2x1
6!=6x5x4x3x2x1
5!=5x4x3x2x1
自訂函數f(n)為n階層
可推論f(n)=n*f(n-1)
Divide:大問題f(n)切割成小問題f(n-1),
直到切割成f(1),f(1)答案就是1
Conquer:將f(n-1)的結果乘以n就可以獲得f(n)的結果
貪婪法-找零問題
Greedy
貪婪法:每步選擇當前最優解,不回溯檢查
🍫
32元
💰
50元
➡️
🪙
1
1元x18
找零會以幣額較大的優先給客人
(假設幣值50、10、5、1)
➡️
🪙
🪙
🪙
🪙
🪙
10
5
1
1
1
問題
子問題
子問題
子問題
+ +
局部最佳解
最佳解
動態規劃-找零問題
Dynamic Programming
動態規劃:適用於重疊子問題,透過記憶化避免重複計算
🍫
32元
💰
50元
如果有幣值9元
➡️
🪙
🪙
🪙
🪙
🪙
10
5
1
1
1
🪙
9
🪙
9
➡️
*不適用貪婪法
動態規劃-找零問題
Dynamic Programming
動態規劃:適用於重疊子問題,透過記憶化避免重複計算
問題
子問題
子問題
+ +
最佳解
找規律
子問題
紀錄子問題答案
查表
最少硬幣湊出18元
最少硬幣湊出17元、13元、9元、8元
(假設幣值50、10、9、5、1)
回溯法-八皇后問題
Backtracking
回溯法:窮舉所有可能,遇到不符合條件則回退
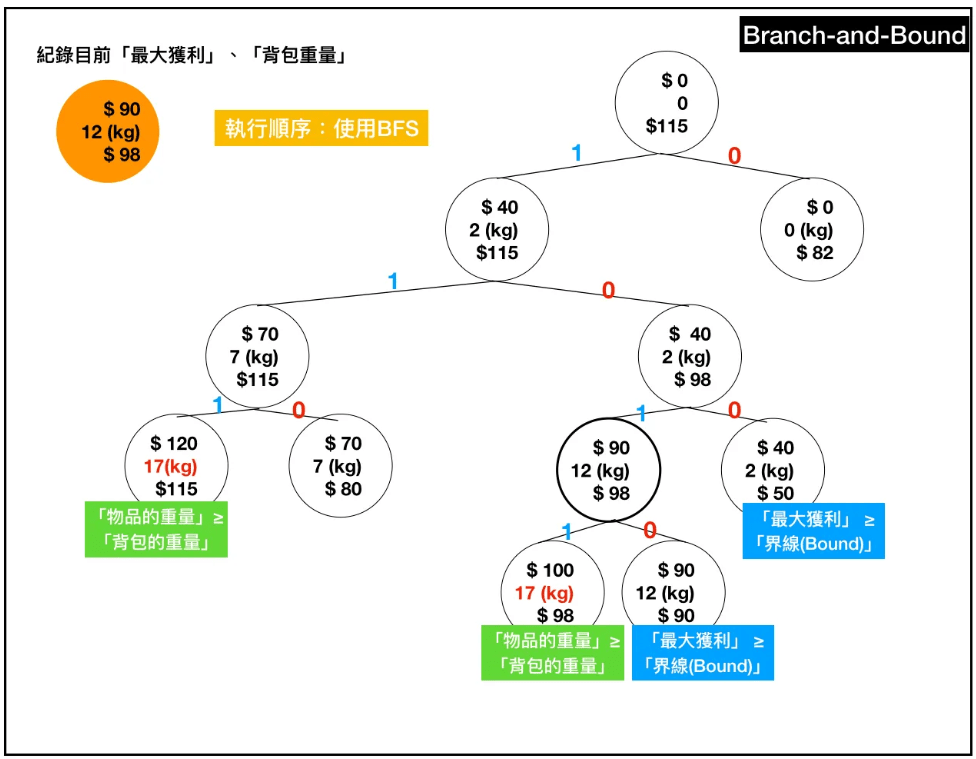
分支定界法
Branch and Bound
分支界限法:窮舉+剪枝,用界限函數排除無效解。
刪數字
給定一個數字num;
刪除其中k個數;
求最小的結果
刪數字
刪數字🌰
num=15726
k=2
1 5 7 2 6
126
刪數字🌰
num=528163579
k=4
528163579
13579
刪數字-觀念
- 小的數字在前
- 大的數字在後
126
162
<
162
*前面數字比後面數字大時刪除
刪數字-觀念
- 小的數字在前
- 大的數字在後
126
162
<
162
*前面數字比後面數字大時刪除
num=23159
k=3
23159
刪數字🌰
num=23159
k=3
23159
刪數字🌰
num=23159
k=3
23159
刪數字🌰
num=23159
k=3
23159
刪數字🌰
num=23159
k=3
23159
刪數字🌰
15
刪數字-stack
2
9
3
1
5
刪數字-stack
2
9
3
1
5
刪數字-stack
2
9
3
1
5
刪數字-stack
9
1
5
刪數字-stack
9
1
5
刪數字-stack
9
1
5
刪數字-stack
9
1
5
刪數字-stack
1
5
vector
| index | 0 | 1 | 2 | 3 | 4 |
| 內容 | 1 | 3 | 5 | 7 |
.size()
.begin()
.end()
.back()
刪數字-程式碼
主程式
int main()
{
string num;
int k;
cin>>num>>k;
string result=del(num,k);
cout<<result;
return 0;
}刪數字-程式碼
函式del(num, k)
string del(string num,int k){
vector<char>s;
for(int i=0;i<num.size();i++){
char n=num[i];
while(!s.empty()&&s.back()>n&&k>0){
s.pop_back();
k--;
}
s.push_back(n);
}
while(k>0&&!s.empty()){
s.pop_back();
k--;
}
string result(s.begin(),s.end());
return result;
}刪數字-程式碼
函式del(num, k)
string del(string num,int k){
vector<char>s;
for(int i=0;i<num.size();i++){
char n=num[i];
while(!s.empty()&&s.back()>n&&k>0){
s.pop_back();
k--;
}
s.push_back(n);
}
while(k>0&&!s.empty()){
s.pop_back();
k--;
}
string result(s.begin(),s.end());
return result;
}#include <bits/stdc++.h>
using namespace std;
string del(string num,int k){
vector<char>s;
for(int i=0;i<num.size();i++){
char n=num[i];
while(!s.empty()&&s.back()>n&&k>0){
s.pop_back();
k--;
}
s.push_back(n);
}
while(k>0&&!s.empty()){
s.pop_back();
k--;
}
string result(s.begin(),s.end());
return result;
}
int main(){
string num;
int k;
cin>>num>>k;
string result=del(num,k);
cout<<result;
return 0;
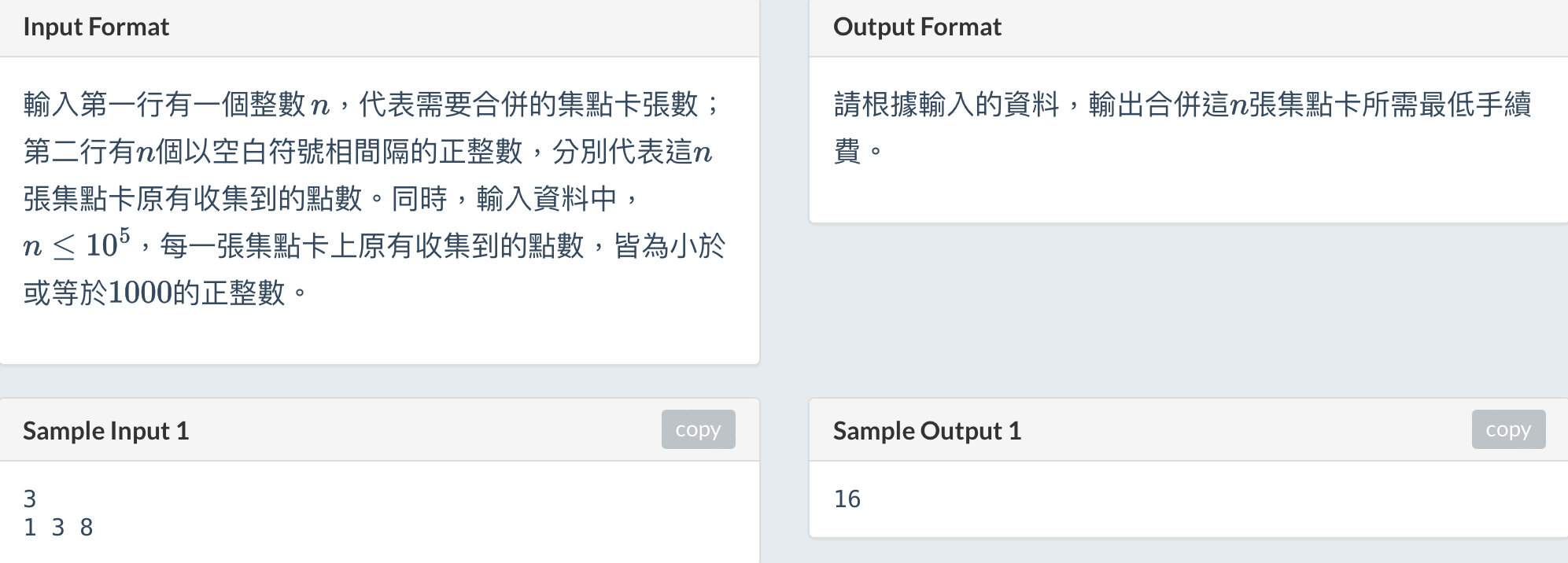
}手續費
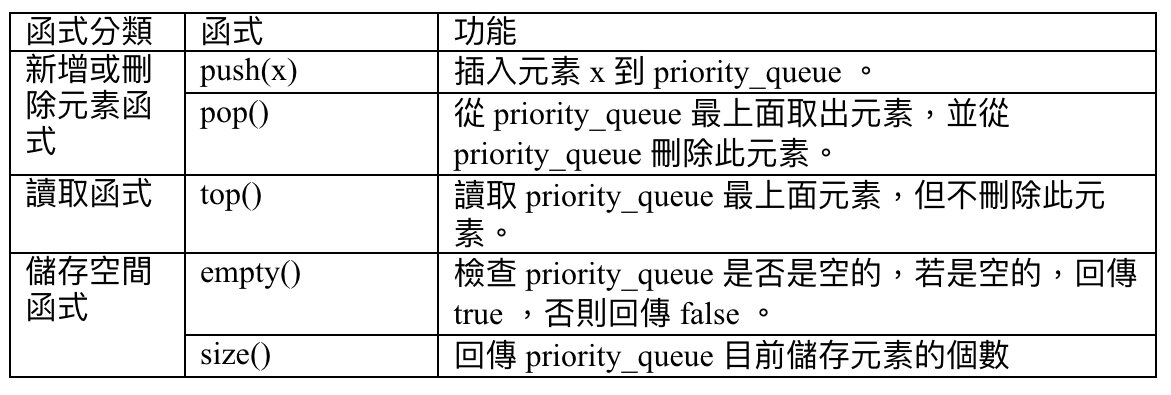
Priority Queue
最大的優先取出priority_queue<int>(預設)
最小的優先取出priority_queue<int,vector<int>,greater<int> >
#include <bits/stdc++.h>
using namespace std;
int main()
{
priority_queue<int> pq1;
priority_queue<int,vector<int>,greater<int> > pq2;
pq1.push(6);
pq1.push(3);
pq1.push(9);
while(!pq1.empty())
{
cout << pq1.top();
pq1.pop();
}
cout<<endl;
pq2.push(6);
pq2.push(3);
pq2.push(9);
while(!pq2.empty())
{
cout << pq2.top();
pq2.pop();
}
return 0;
}963
369

#include <bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int> > pq;
int main(){
int n,point;
long long money=0;
cin>>n;
while(!pq.empty()) pq.pop();
for(int i=0;i<n;i++){
cin>>point;
pq.push(point);
}
while(1){
int a,b;
a=pq.top();
pq.pop();
b=pq.top();
pq.pop();
money+=a+b;
pq.push(a+b);
if (pq.size()==1) break;
}
cout<<money<<endl;
}貪婪演算法
By chainy
貪婪演算法
- 161



