data-driven simulation-based galaxy evolution
Yale galaxy lunch --- Nov 20, 2019
ChangHoon Hahn
arXiv:1809,01665
arXiv:1910.01644
everything we've learned so far from galaxy surveys
... in 30 sec
* about massive galaxies at z<2
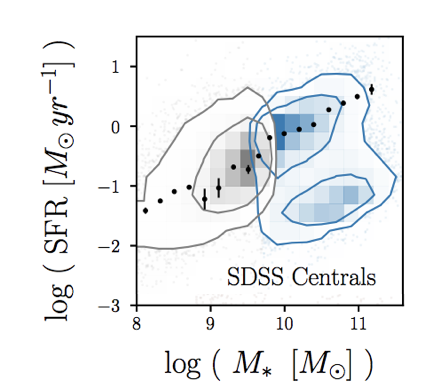
galaxies broadly fall into two categories
star forming galaxies
late-type, disk-like, blue
quiescent galaxies
early-type, elliptical, red
PRIMUS
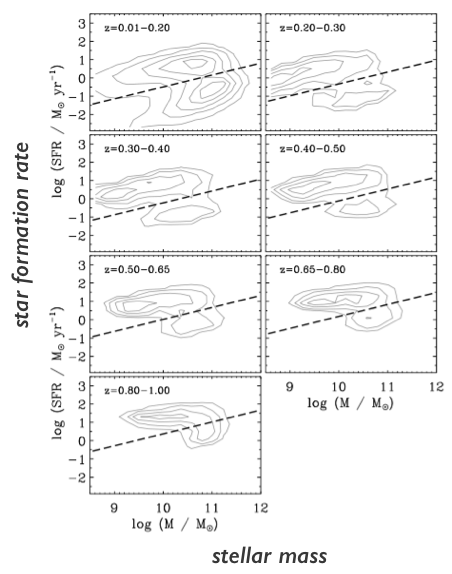
star-forming galaxies lie on the star-forming sequence
Hahn+(2019a)
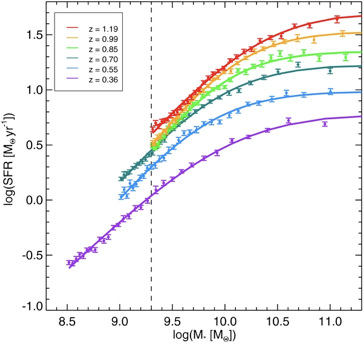
overall decline in star formation over time
Lee+(2015)
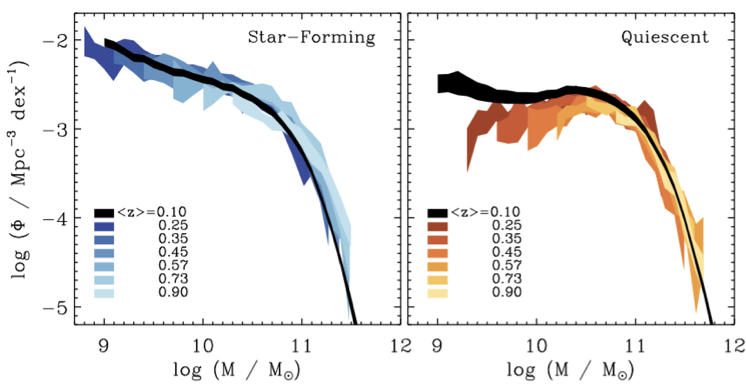
fewer massive star-forming galaxies
more quiescent galaxies over time
Moustakas+(2013)
PRIMUS
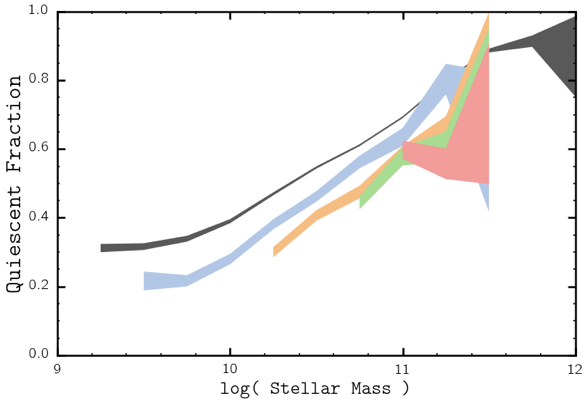
log (stellar mass)
quiescent fraction
SDSS z~0
PRIMUS z~0.9
state-of-the-art galaxy formation models roughly reproduce these relations
credit: Illustris TNG
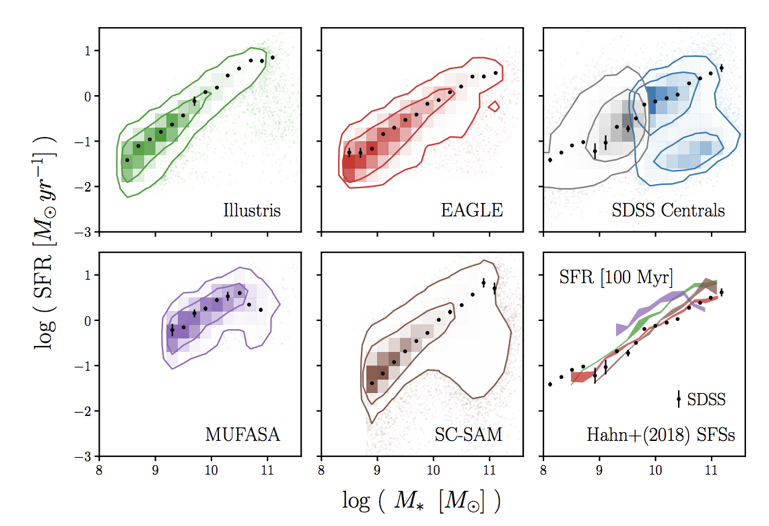
simulations can produce the star-forming sequence (SFS)
Hahn+(2019a)
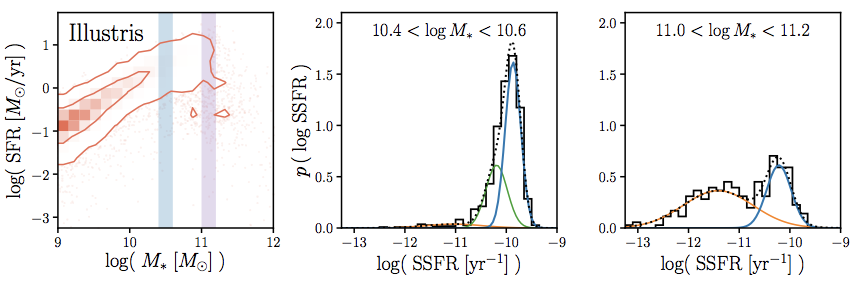
data-driven GMM-based method for identifying the
star-forming sequence
Hahn+(2019a)
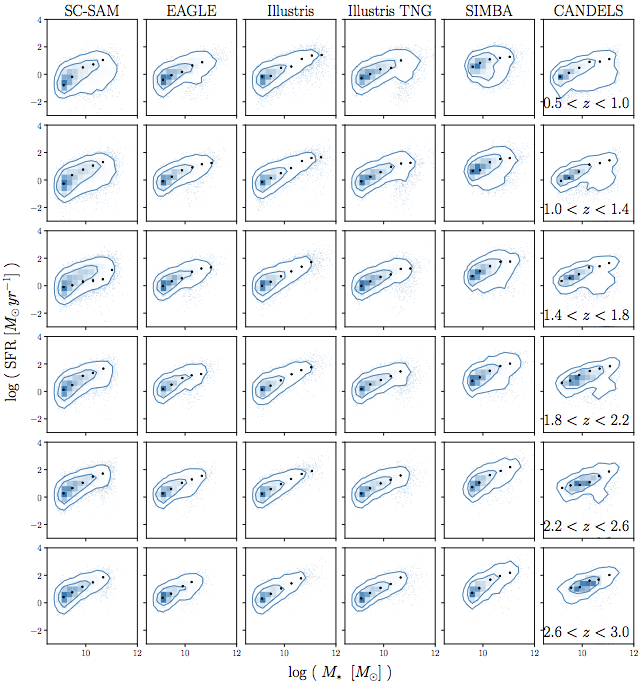
out to high redshifts
Choi, CH+(in prep)
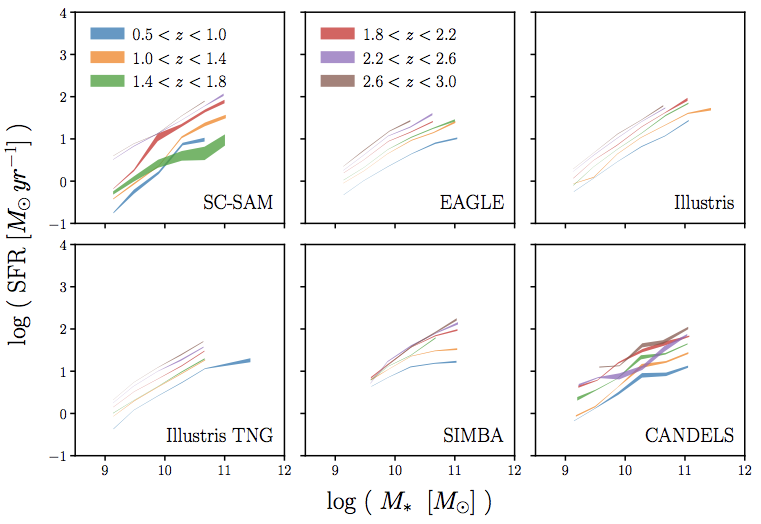
Choi, CH+(in prep)
*...don't worry about SC-SAM
they can also produce the SFS z evolution
can we make galaxy formation/evolution into an inference problem?
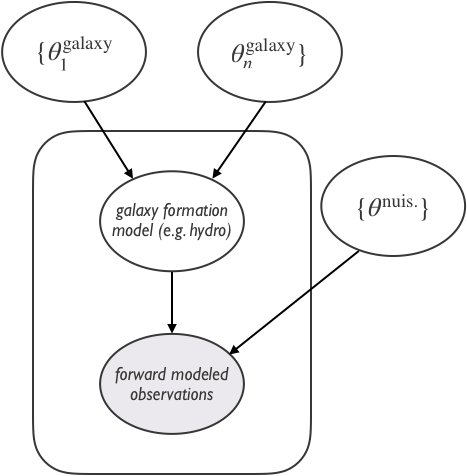
Isolated and Quenched collaboratory: framework for forward modeling observations
computational expensive*
... not easy to interpret
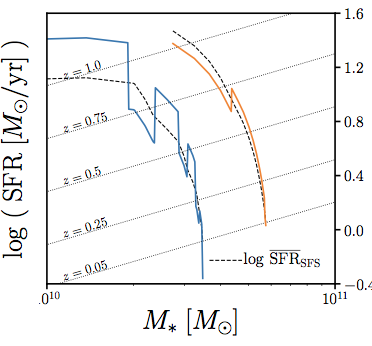
e.g. why do SFS in simulations differ by ~5x?
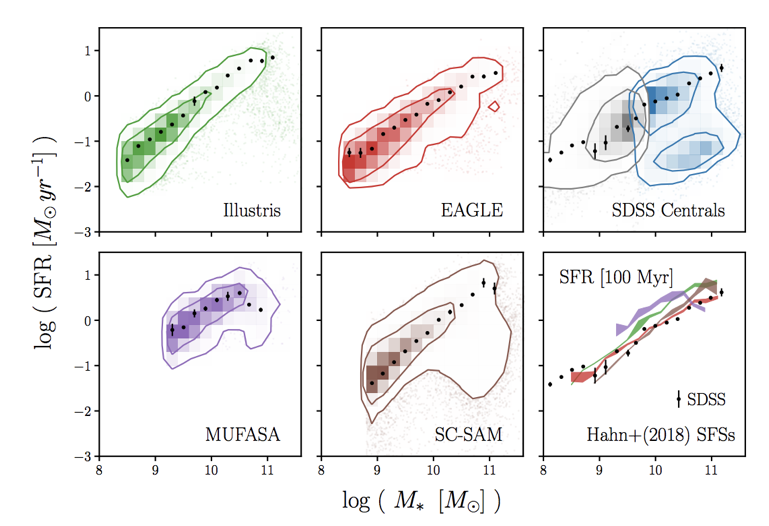
Hahn+(2019a)
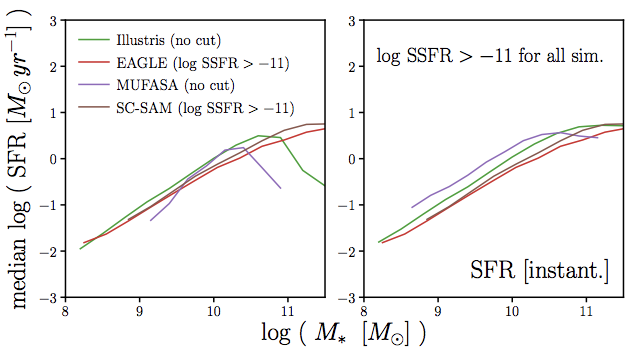
same methods as Somerville & Davé (2015)
why we need data-driven methods
empirical models: ΛCDM + observed evolution of galaxies
credit: Wechsler & Tinker (2018)
computationally cheap
easy to interpret
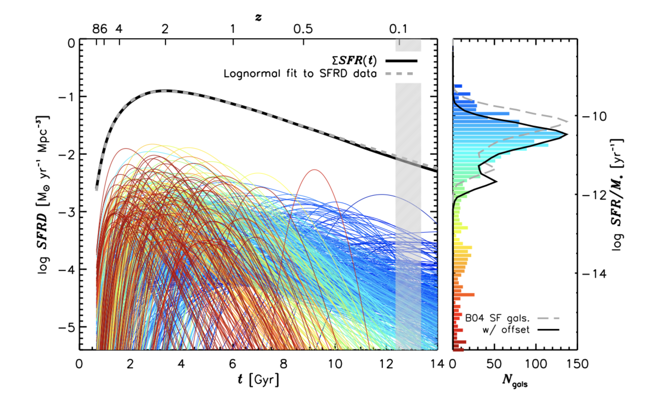
Abramson+(2015, 2016)
their claim: loosely constrained log-normal SFH can reproduce SMF, SFS, etc. at z<6
they get stellar masses from the star formation histories but ...what about the stellar-to-halo mass relation?
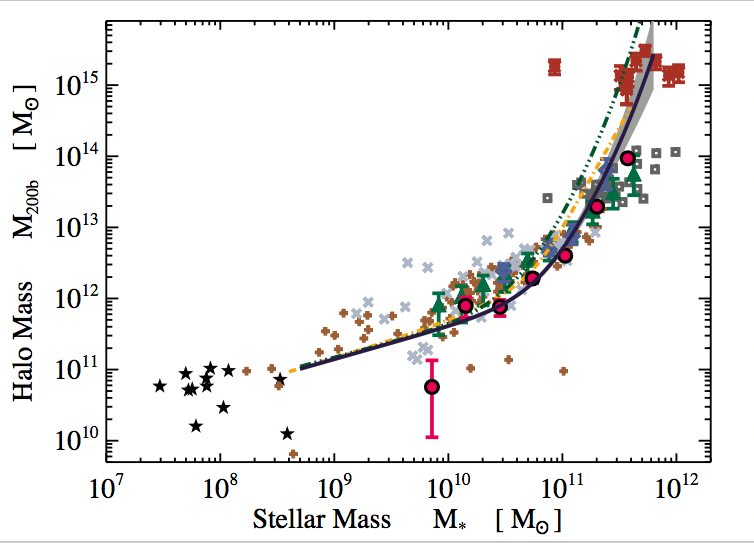
credit: Alexie Leauthaud
for star forming central galaxies
the connection between star formation histories and stellar masses constrained by star forming sequence
the stellar-to-halo mass relation constrains the connection between stellar masses and halo mass
we can constrain star formation histories using the
star-forming sequence and stellar-to-halo mass relation!
star-forming centrals initialized using SMF and SFS at z~1
M* from subhalo-halo abundance matching to SMF
SFR from SFS with 0.3 dex scatter
once quenched always quenched
\log~{\rm SFR}(M_*, t) = \log~{\rm SFR}_{\rm SFS}(M_*, t) + \Delta \log~{\rm SFR}(t)
the connection between star formation histories and stellar masses constrained by star forming sequence
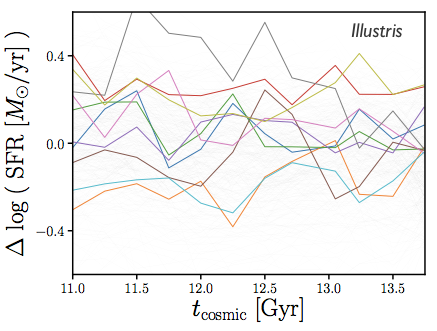
star-forming centrals in Illustris
\log~{\rm SFR}(M_*, t) = \log~{\rm SFR}_{\rm SFS}(M_*, t) + \Delta \log~{\rm SFR}(t)
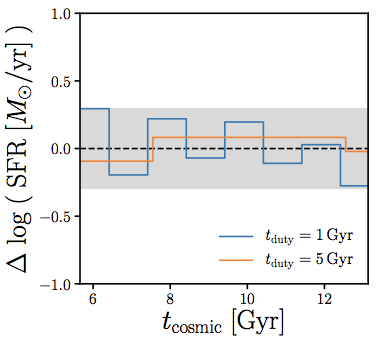
star formation duty cycle: star formation histories that vary on tduty Gyr timescales
M_*(t) \propto \int\limits_{t_0}^{t}{\rm SFR}(M_*, t'){\rm d}t' + M_0
models that reproduce* SMF and SFS at z~0
but have different tduty
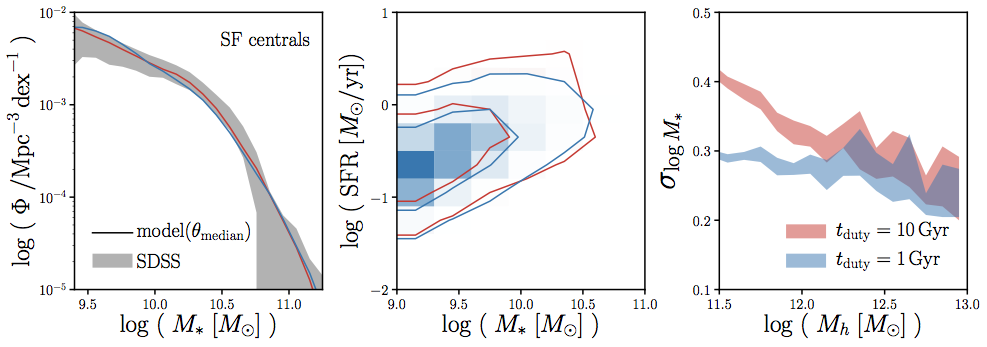
*using Approximate Bayesian Computation (more on this later!)
predict different scatter in SHMR
\sigma_{M_*|M_h}
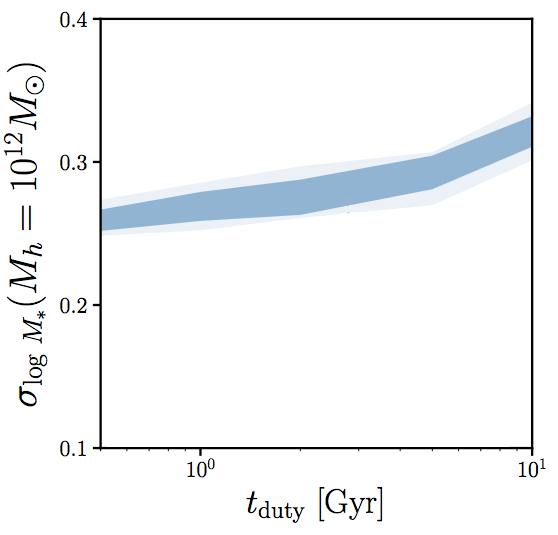
scatter in SHMR at low Mh is sensitive to tduty (i.e. timescale of SF variability)
\sigma_{M_*|M_h=10^{12}M_\odot}
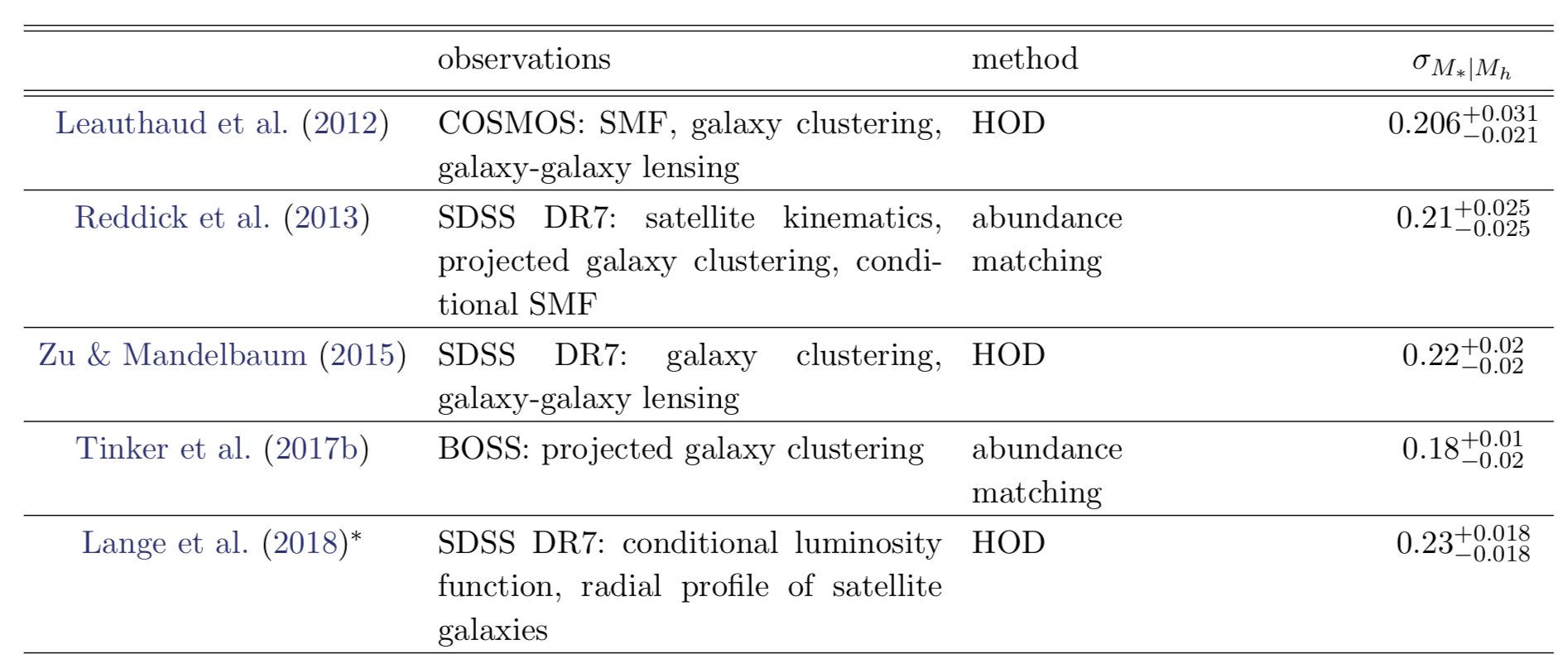
observations find a tight ~0.2 dex scatter in SHMR
\sigma_{M_*|M_h=10^{12}M_\odot}
we add galaxy assembly bias to our model:
star formation histories correlate with Mh history
\log~{\rm SFR}(M_*, t) = \log~{\rm SFR}_{\rm SFS}(M_*, t) + \Delta \log~{\rm SFR}(t)
\Delta \log~{\rm SFR}(t)
\Delta M_h(t) = M_h(t) - M_h(t-t_{\rm dyn})
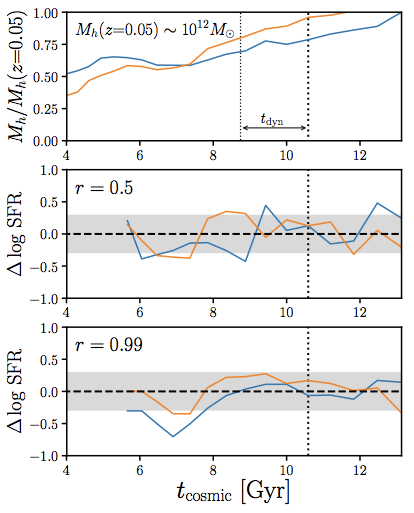
similar to Rodríguez-Pubela+(2016), Behroozi+(2019)
correlated to
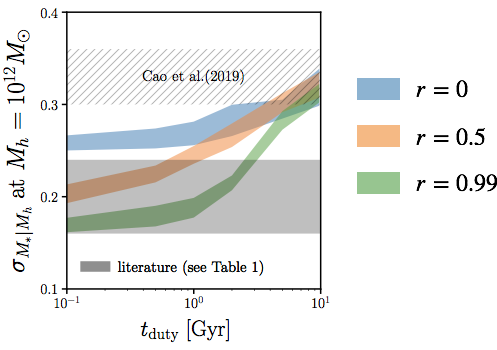
tighter scatter in SHMR for stronger galaxy assembly bias
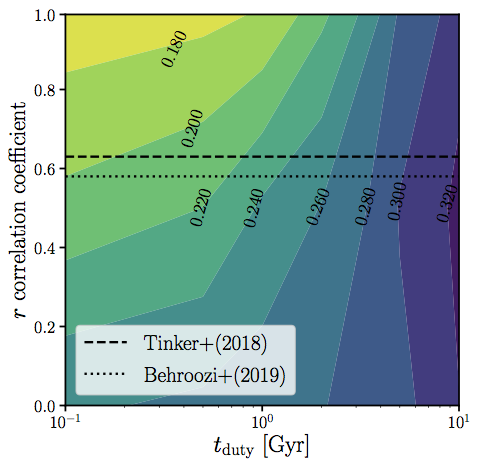
scatter in SHMR sensitive to tduty and rassembly bias
r~0.6 from literature ... tduty < 0.2 Gyr ?
new constraints find larger SHMR >0.3dex scatter
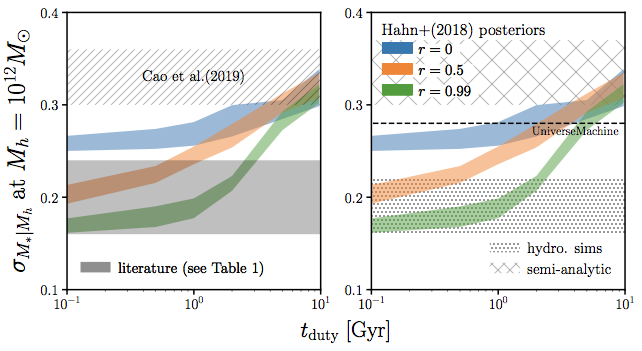
also no consensus among simulations
tight constraint on tduty currently limited by tensions in both observations and simulations
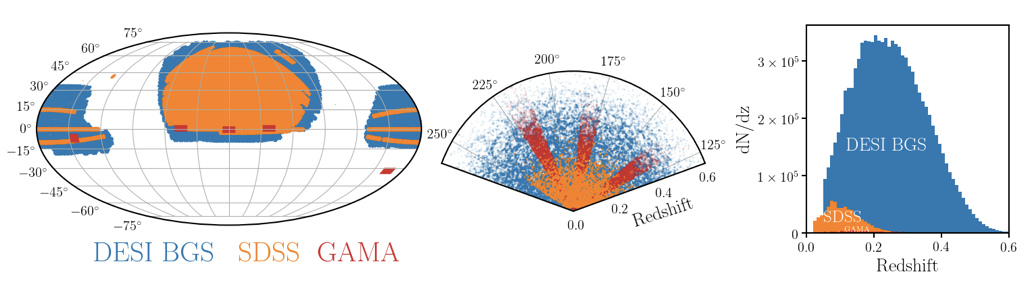
DESI Bright Galaxy Survey
14,000 sq.deg
magnitude-limited to r~20
10 million galaxies
DESI first light!
<1% sky subtraction
the PRObabilistic Value-Added BGS
(PROVABGS)
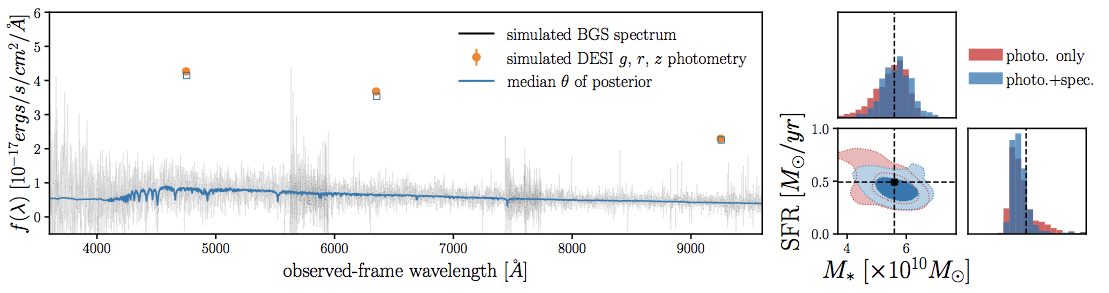
10 million posteriors of galaxy properties from jointly fitting photometry+spectroscopy
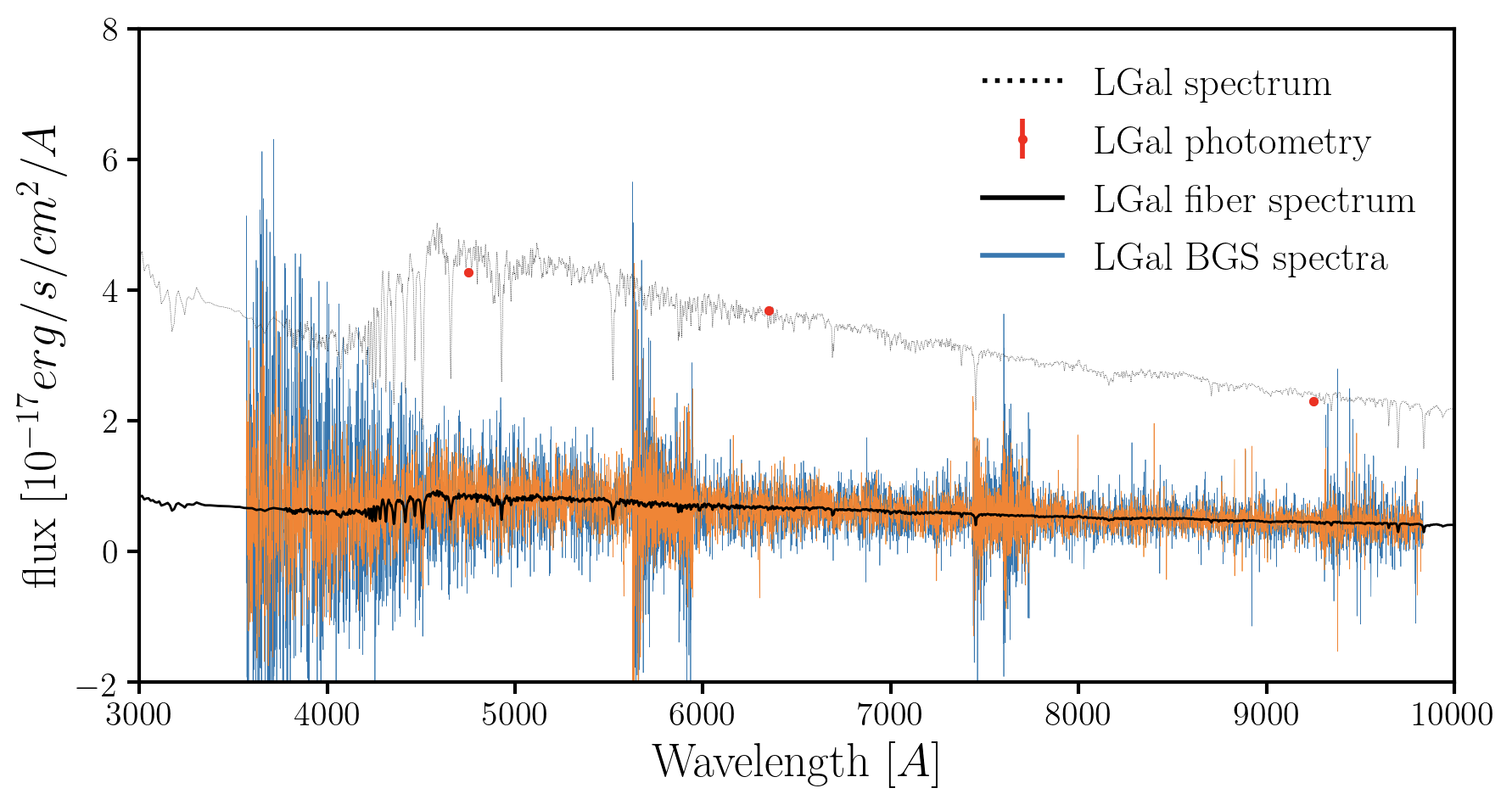
DESI GQP Mock Challenge (MoCha) is currently underway to determine the PROVABGS analysis pipeline
w/ Malgorzata Siudek (IFAE Barcelona), James Kwon (UC Berkeley)
MCMC using speculator, a PCA neural network SPS emulator
percent-level accuracy and >1000x faster
Alsing...CH+(in prep)
galaxy formation models are computationally expensive
possible to make galaxy evolution into an inference problem with simulation-based inference
*also known as "likelihood-free" inference
x
θ
consider p(x,θ) for 1D data and 1D parameter
*probably an ideal situation
likelihood p(x|θ)
x
θ
*probably an ideal situation
xobs
posterior p(θ|xobs)
consider p(x,θ) for 1D data and 1D parameter
x
θ
xobs
naive approximate bayesian computation
wastes a lot of simulations ... there are smarter methods (e.g. ABC-PMC; Hahn+2017a,c,2019b)
x
θ
direct density estimation SBI can estimate posteriors much more efficiently (e.g. using ICA and GMM; Hahn+2019c)
only tip of the SBI iceberg!
Density Estimation LFI (Alsing+2019),
ABC with Conditional Density Estimation (Izbicki+2018),
Sequential Neural Posterior Estimation (Lueckmann+2019),
Bayesian Optimization LFI (Gutmann & Corannder 2016),
Inference Aware Neural Optimization (de Castro & Dorigo 2018)
...
the LFI Taskforce is developing new methods for SBI tailored to astronomy
logo credit: @danielhey
w/ Arin Avsar, Tess Werhane, James Zhu, Vanessa Boehm, Francois Lanusse, Jia Liu (Berkeley)
Virginia Ajani (CEA), Will Coulton (Cambridge), Chieh-An Lin (Edinburgh), Nesar Ramachandra (ANL)
empirical models are cheap and easy to interpret:
e.g. constraining SF variability timescale from SHMR (Hahn+2019c)
DESI Bright Galaxy Survey (PROVABGS) --- 10 million galaxies
hydro sims and SAMs are expensive and difficult to interpret
...plenty of room for improvement (Hahn+2019a)
e.g. tighter constraints on tduty, tquench (Hahn+2017c), assembly bias, hierarchical Bayesian modeling
SBI methods will enable direct inference from galaxy surveys
credit: desi.lbl.gov
IQ collaboratory, ABC, DELFI
yale2019
By ChangHoon Hahn
yale2019
talk on star forming central galaxies at Yale galaxy lunch Nov 20, 2019
