Post-quantum Cryptography
Chen-Mou Cheng
BTQ
Review: (EC)DLP cryptography
- The discrete logarithm problem in a cyclic group \(G\)
- Given \(h\in G\) and a generator \(g\in G\), find an integer \(x\in\mathbb Z/q\mathbb Z\) s.t. \(h=g^x\::=\underbrace{g\cdot g\cdots g}_{x\text{ times}}\), where \(q=|G|\)
- E.g., Diffie-Hellman key exchange (1976)
\(x\leftarrow\mathbb Z/q\mathbb Z\)
\(h_1\leftarrow g^x\)
\(s\leftarrow h_2^x=(g^y)^x=g^{yx}\)
\(\xrightarrow{\hspace*{2em}h_1\hspace*{2em}}\)
\(\xleftarrow{\hspace*{2em}h_2\hspace*{2em}}\)
\(y\leftarrow\mathbb Z/q\mathbb Z\)
\(h_2\leftarrow g^y\)
\(s\leftarrow h_1^y=(g^x)^y=g^{xy}\)
Shor's algorithm on quantum computers:
will break them all

How about QKD?
Quantum key distribution
Toy example of BB84

Limitations of QKD
- Limited functionalities
- No digital signatures (yet)
- Need to physically ship qubits
- No-Cloning Theorem!
- Need trusted relays to go beyond ~100km
Post-quantum cryptography
- Hash-based signatures (Merkle, late 1970s)
- Code-based encryptions (McEliece, 1978)
- Multivariate cryptography (松本 & 今井, 1988)
- Lattice-based cryptography (Ajtai, 1996)
- Isogeny-based cryptography
- De Feo, Jao, & Plut @ PQCRYPTO'11, Taipei, Taiwan
- SIDH/SIKE has been broken, but others not (yet)
Lamport's hash-based
one-time signature
- Key generation
- Private key: \((s_0,s_1)\)
- Public key: \((p_0,p_1)=\left(H(s_0),H(s_1)\right)\)
- To sign a message \(m\in\{0,1\}\), the signature is simply \(s_m\)
- To verify, check whether \(H(s_m)\stackrel{?}{=}p_m\)
Merkle tree
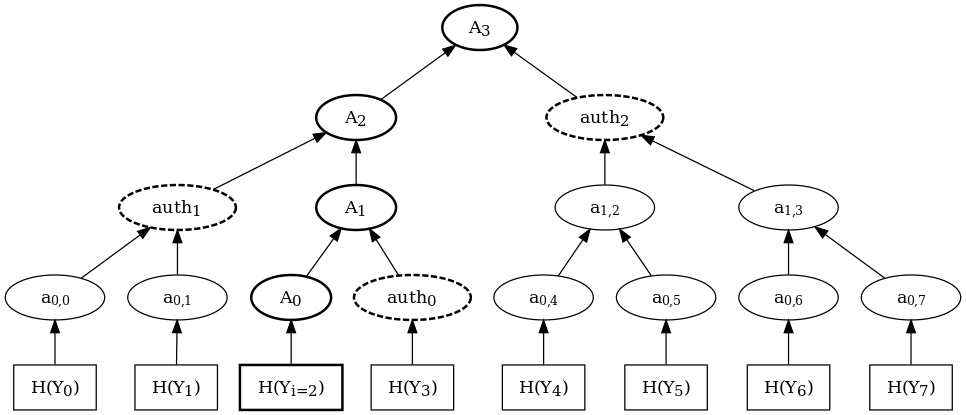
Stateful vs. stateless
- Can commit OTS PKs to Merkle tree
- Public key = Merkle root
- Each signature includes OTS signature + authentication path to Merkle root
- Going stateless (Goldreich, 1987)
- Lots of pseudorandom, on-demand tree of trees
- Each signature additionally includes chain of (hash-based) signatures of certificate authorities
Multivariate cryptography
- Typical public key \( P:k^n\rightarrow k^m \) that sends \[ \mathbf w\in k^n\stackrel{S}{\mapsto}\mathbf x=\mathbf M_S\mathbf w+\mathbf c_S\stackrel{Q}{\mapsto}\mathbf y\stackrel{T}{\mapsto}\mathbf z=\mathbf M_T\mathbf y+\mathbf c_T\in k^m \]
- \( S,T \) are affine, typically invertible
- Central map \( Q \) is nonlinear, often quadratic
- Hence \( P=T\circ Q\circ S \) is a polynomial system over \( k \)
- Security based on hardness of nonlinear system solving and isomorphism of polynomials
The shortest vector problem on euclidean lattices
- A lattice is a discrete subset of \(\mathbb R^n=\text{span}(\mathbf b_1,\ldots,\mathbf b_n)\): \[\mathcal L=\left\{\sum_{i=1}^na_i\mathbf b_i:a_i\in\mathbb Z\right\}=\Big\{\mathbf a^T\mathbf B:\mathbf a\in\mathbb Z^n\Big\}\]
- SVP: Given a basis of a lattice \(\mathcal L\) and a norm \(N\) (often \(L^2\)), find the shortest nonzero vector in \(\mathcal L\) as measured by \(N\)
LWE
Learning with error
SIS
Short integer solution
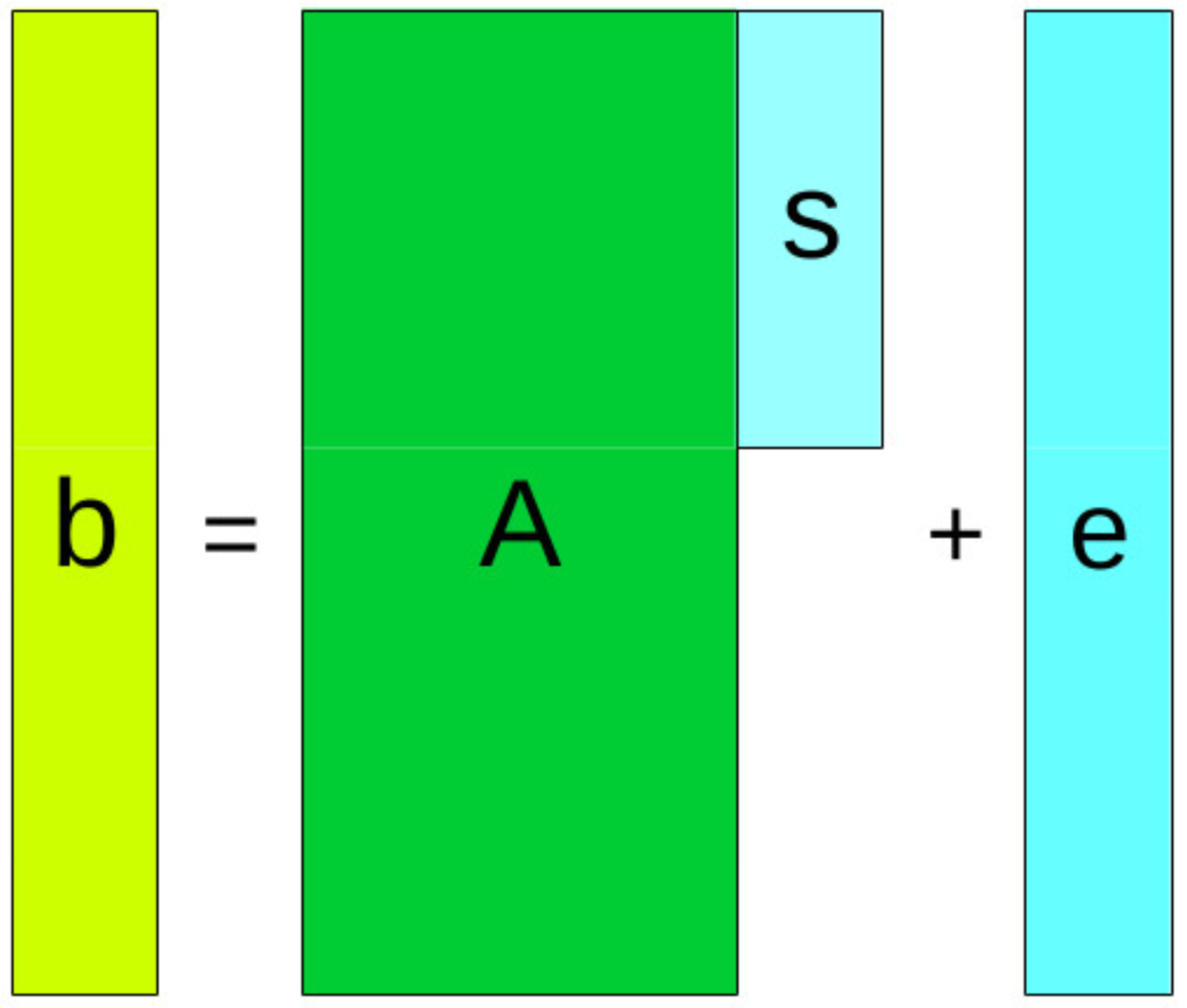
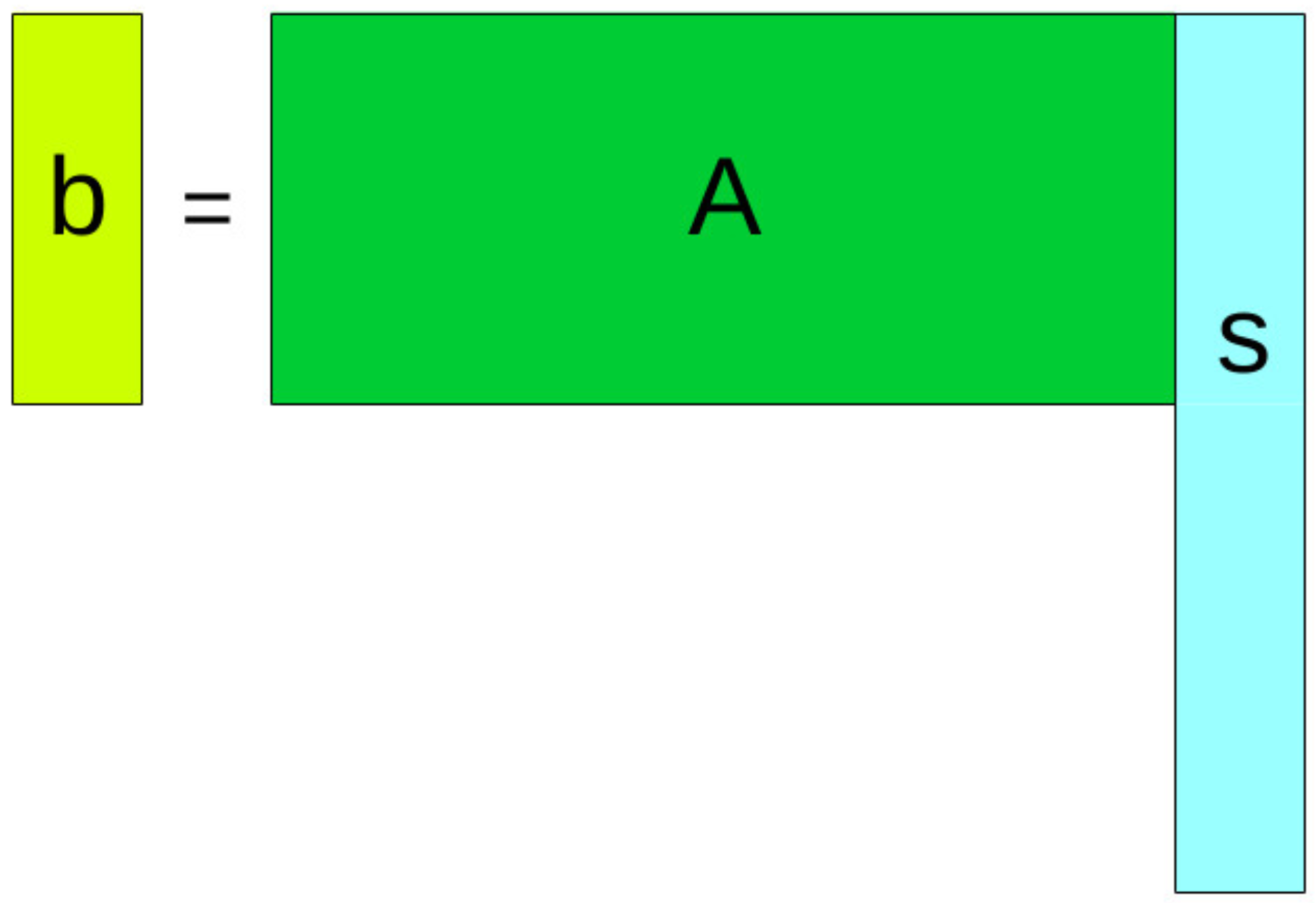
Ideal lattices
- How to "compress" \(\mathbf A\)?
- Build \(\mathbf A\) from a basis for the ideal generated by \(\mathbf a\) and \(X\) in a quotient ring, e.g., \(\mathbb Z_q[X]/(X^n-1)\): \[ \begin{aligned} \mathbf{As} & =\begin{bmatrix} \mathbf a & \mathbf aX & \cdots & \mathbf aX^{n-1} \end{bmatrix}\begin{bmatrix} s_0 & \cdots & s_{n-1} \end{bmatrix}^T \\ & =s_0\mathbf a + s_1\mathbf aX + \cdots + s_{n-1}\mathbf aX^{n-1} \\ & =\mathbf a\left(s_0+s_1X+\cdots+s_{n-1}X^{n-1}\right) \end{aligned} \]
- Core computation: From matrix-vector multiplication to polynomial multiplication
PQCRYPTO'16

- Feb 2016: Announced in PQCRYPTO
- Need to run on classical, non-quantum computers
- Wide spectrum: From extremely constrained devices to limited communication bandwidth
- July 2022: To standardize 4 algorithms
- July 2023: To consider 40 additional signature schemes
| CRYSTALS-Kyber | Lattice (MLWE) | KEM |
| CRYSTALS-Dilithium | Lattice (MLWE) | Signature |
| Falcon | Lattice (NSIS) | Signature |
| SPHINCS+ | Hash-based | Signature |


Beyond KEM & signature:
Introducing zk-SNARK
- Noninteractive ARgument of Knowledge
- Prover sends to Verifier \( f,x,y, \) and a proof \( \pi \), which proves that Prover knows a (secret) \( \color{red}w\color{black} \) s.t. \( f(x,\color{red}w\color{black})=y \)
- Succinct if \( \pi \) is "small" compared with \( f, \) e.g., \( |\pi|=O(\log|f|) \)
- Zero-Knowledge if Verifier learns nothing about \( \color{red}w\color{black} \) beyond its existence and what can be inferred from \( f(x,\color{red}w\color{black})=y \)
zk-SNARKing 自然人憑證
- CA signs Cert: "Batman was born on Jan 1, 1974"
- \( f(x,\color{red}w\color{black})=1 \) if and only if:
- \( \color{red}w\color{black} \) is a valid certificate signed by CA
- \( \color{red}w\color{black} \) says as of today, \( x \) is over 18 years old
- Beers for Batman if \( \pi \) proves \( f(\text{Batman},\color{red}\text{Cert}\color{black})=1 \)
zk-SNARKing C2PA
-
Coalition for Content Provenance and Authenticity
- Camera signs all photos taken: \( s=\text{sign}_C(p) \)
- Publisher/consumer verifies: \( \text{verify}_C(p,s)? \)
- What if \( p'=f(p) \) where \( f \) crops, resizes, rotates, etc?
- \( \pi \): "I know \( \color{red}p\color{black},\color{red}s\color{black} \) s.t. \( \text{verify}_C(\color{red}p\color{black},\color{red}s\color{black}) \) & \( p'=f(\color{red}p\color{black}) \)"
- For zk-SNARKs, \( |\pi|\ll |f|=o(|\color{red}p\color{black}|) \)
How to play fair over internet
- Cryptographic commitment
- Commit: \( c=\text{commit}(r,m) \)
- Verify: \( \text{verify}\Big(r,m,c\Big)? \)
- Security properties
- Hiding: difficult to find \( m \) given \( c=\text{commit}\left(r,m\right) \)
- Binding: difficult to find \( r',m'\neq m \) s.t. \( \text{verify}\Big(r',m',\text{commit}(r,m)\Big) \)
Proving \( f(x)=y \)
- Functional commitment
- \( c=\text{commit}(r,f) \)
- \( (y,\pi)=\text{eval}(r,f,x) \)
- \( \text{verify}\Big(c,x,y,\pi\Big) \) iff \( \exists r\text{ s.t. }c=\text{commit}(r,f) \) and \( f(x)=y \)
- Example (Merkle tree)
- Leaves \( y_0,y_1,\ldots,y_{n-1} \) define \( f:\Big\{0,1,\ldots,n-1\Big\}\rightarrow Y \)
- Authentication path encodes (binary expansion of) \( i\in\Big\{0,1,\ldots,n-1\Big\} \) and thus proves \( f(i)=y_i \)
Toy example
- Prover: "I know (primes) \( \color{red}p\color{black},\color{red}q\color{black} \) s.t. \( n=\color{red}pq\color{black} \)"
- Prover commits to three polynomial functions: \[ \color{red}r_p\color{black}X+\color{red}p\color{black},\color{red}r_q\color{black}X+\color{red}q\color{black},\text{ and }\color{red}r_pr_q\color{black}X^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})X+n \]
- Verifier challenges Prover with random \( r \) and checks whether \( (\color{red}r_p\color{black}r+\color{red}p\color{black})(\color{red}r_q\color{black}r+\color{red}q\color{black})\stackrel{?}{=}\color{red}r_pr_q\color{black}r^2+(\color{red}r_pq\color{black}+\color{red}pr_q\color{black})r+n \)
- Lemma [Schwartz-Zippel] \[ \text{Pr}_{r\in k}\Big(f(r)=g(r)\Big)\leq\frac{d}{|k|}\text{ for }f\neq g\text{ with }\deg f,\deg g\leq d \]
Thank you!
Questions or comments?
Post-quantum cryptography
By Chen-Mou Cheng
Post-quantum cryptography
- 172



