Output Supply
and Labor Demand
Christopher Makler
Stanford University Department of Economics
Econ 50 | Lecture 19
Optimization
What is an agent's optimal behavior for a fixed set of circumstances?
x_1^*
x_2^*
q^*
L^*
Utility-maximizing bundle for a consumer
Profit-maximizing quantity for a firm
Profit-maximizing input choice for a firm
Comparative Statics
How does an agent's optimal behavior change when circumstances change?
x_1^*
x_2^*
q^*
L^*
Utility-maximizing bundle for a consumer
Profit-maximizing quantity for a firm
Profit-maximizing input choice for a firm
x_1^*(p_1\ |\ p_2,m)
x_2^*(p_2\ |\ p_2,m)
q^*(p\ |\ w)
L^*(w\ |\ p)
Assumptions
We will be analyzing a
competitive (price-taking) firm
in the short run
- output price \(p\)
- wage rate \(w\)
Today's Agenda
1. Choosing the \(q^*\) and \(L^*\) for a fixed \(p\) and \(w\)
4. Edge Cases
2a. Deriving output supply
as a function of \(p\),
holding \(w\) constant
2a. Deriving labor demand
as a function of \(w\),
holding \(p\) constant
3a. Analyzing how a change in \(w\)
shifts the supply curve
3b. Analyzing how a change in \(p\)
shifts the labor demand curve
[ MOVEMENT
ALONG CURVES]
[ SHIFTS OF
CURVES]
We'll stick with our same function
f(L,K) = \sqrt{LK}
\overline K = 32
L(q) = {q^2 \over K}
MP_L = \frac{1}{2}\sqrt{K \over L}
L(q) = {q^2 \over 32}
MP_L = \sqrt{8 \over L}
f(L) = \sqrt{32L}
1. Optimization with Fixed Price and Wage Rate
Profit as a function of quantity
Profit as a function of labor
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
\pi(q) = 12q - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = 12 - {1 \over 2}q = 0
r(L) = p \times f(L) = 12 \sqrt{32L}
1. Costs and revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
q^* = 24
L^* = 18
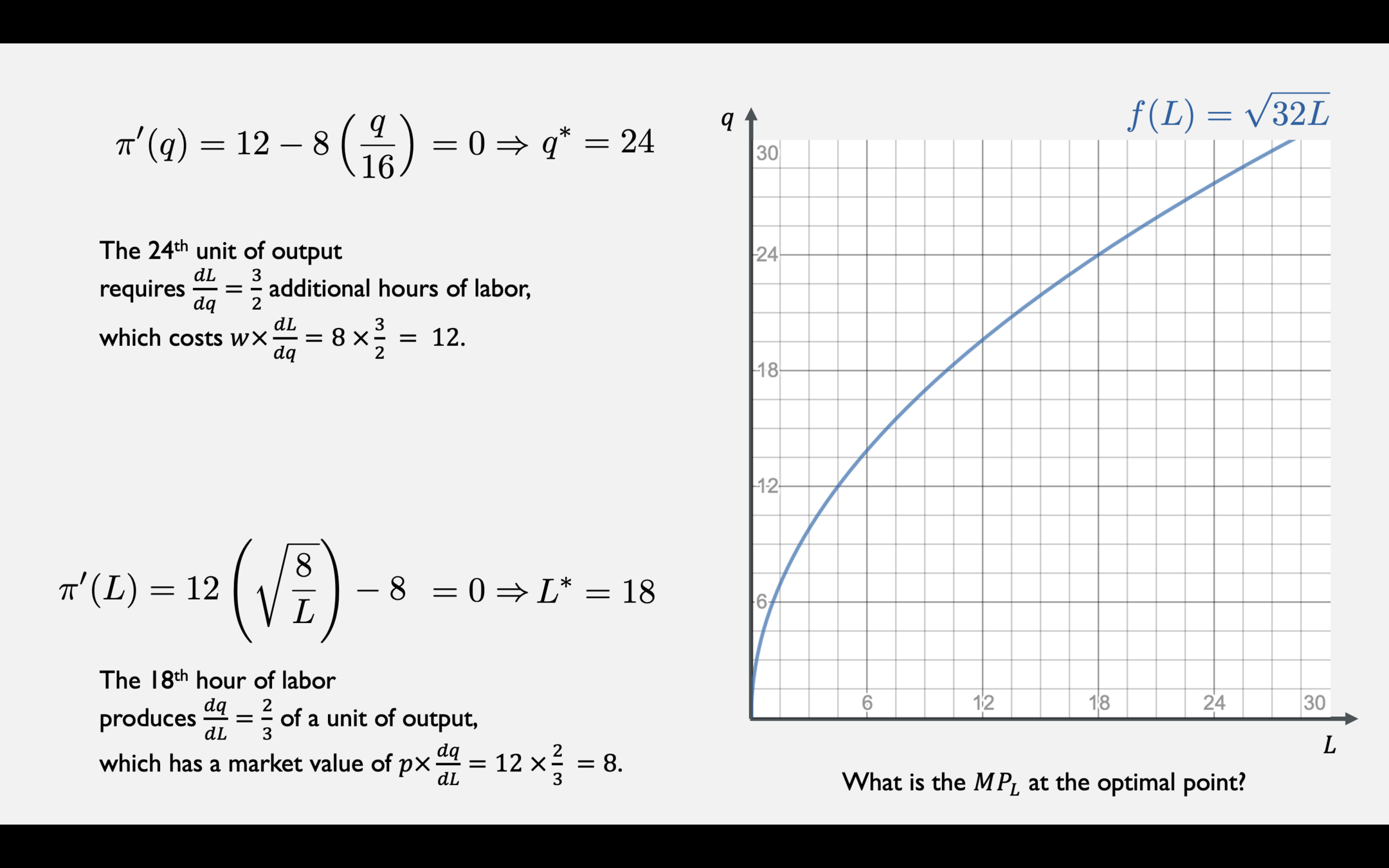
Profit two ways when \(p = 12\), \(w = 8\), \(r = 2\), and \(\overline K = 32\)
c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
r(q) = pq = 12q
c(L) = wL + r\overline K = 8L + 64
MP_L = \tfrac{2}{3}
2a. Output Supply as a Function of \(p\) with Fixed \(w\)
When price is fixed at 12
For a general price
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
\pi(q) = 12q - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = 12 - {1 \over 2}q = 0
r(q) = pq
\pi(q) = pq - (64 + \tfrac{1}{4}q^2)
\pi^\prime(q) = p - {1 \over 2}q = 0
q^* = 24
q^*(p) = 2p
Profit-Maximizing Output Choice when \(w = 8\), \(r = 2\), and \(\overline K = 32\)
c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
r(q) = pq = 12q
c(q) = wL(q) + r\overline K = {1 \over 4}q^2 + 64
NUMBER
FUNCTION
f(L,K) = \sqrt{LK}, \overline K = 32
64 + {1 \over 4}q^2
{1 \over 2}q
pq
\pi(q) = \ \ \ \ \ - [\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ]
\pi^\prime(q) = \ \ \ - \ \ \ \ \ \ \ \ = 0
p
TR
TC
MR
MC
Take derivative and set = 0:
Solve for \(q^*\):
q^*(p) = 2p
SUPPLY FUNCTION
When \(p = 4\), this function says that the firm should produce \(q = 8\).
If it does this...
pollev.com/chrismakler
We just showed that for a firm with the cost function 𝑐(𝑞)=64+14𝑞2c(q)=64+41q2, the profit-maximizing choice when 𝑝=4p=4 is to produce 𝑞=8q=8. If the firm does this:
Text
2b. Labor Demand as a Function of \(w\) with Fixed \(p\)
When wage is fixed at 8
For a general wage
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
Profit-Maximizing Labor Choice when \(p = 12\), \(r = 2\), and \(\overline K = 32\)
NUMBER
FUNCTION
r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (wL + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - w = 0
L^* = {1152 \over w^2}
c(L) = wL + r\overline K = wL + 64
r(L) = p \times f(L) = 12 \sqrt{32L}
\pi(L) = 12\sqrt{32L} - (8L + 64)
\pi^\prime(L) = 12 \times \sqrt{8 \over L} - 8 = 0
L^* = 18
c(L) = wL + r\overline K = 8L + 64
f(L,K) = \sqrt{LK}, \overline K = 32
wL + 64
w
12\sqrt{32L}
\pi(L) = \ \ \ \ \ \ \ \ \ \ \ \ \ - [\ \ \ \ \ \ \ \ \ \ \ \ \ \ ]
\pi^\prime(q) = \ \ \ \ \ \ \ \ \ \ - \ \ \ \ = 0
12\sqrt{8 \over L}
TR
TC
MRPL
MC
Take derivative and set = 0:
Solve for \(L^*\):
L^*(w) = {1152 \over w^2}
LABOR DEMAND FUNCTION
(over to powerpoint for a moment)
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
c(q) = wL(q) + r \overline K
1. Costs for general \(w\) and revenue for general \(p\)
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
\pi(q) = pq - [wL(q) + r\overline K]
\pi^\prime(q) = p - w \times {dL \over dq} = 0
r(L) = p \times f(L)
\pi(L) = p\times f(L) - [wL + r\overline K]
\pi^\prime(L) = p \times {dq \over dL} - w = 0
p = w \times {dL \over dq}
p \times {dq \over dL} = w
\text{Profit }\pi = pq - [wL + rK]
r(q) = p \times q
c(L) = wL + r \overline K
[cost of labor required for \(q\) units of output]
[revenue of output produced by \(L\) hours of labor]
MARGINAL COST (MC)
MARGINAL REVENUE PRODUCT OF LABOR (MRPL)
"Keep producing output as long as the marginal revenue from the last unit produced is at least as great as the marginal cost of producing it."
"Keep hiring workers as long as the marginal revenue from the output of the last worker is at least as great as the cost of hiring them."
p = MC
w = MRP_L
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
L^*(w\ |\ p) = 8 \left({p \over w}\right)^2
LABOR DEMAND FUNCTION
f(L,K) = \sqrt{LK}, \overline K = 32
L^*(w\ |\ p) = 8 \left({p \over w}\right)^2
LABOR DEMAND FUNCTION
q^*(p\ |\ w) = {16p \over w}
SUPPLY FUNCTION
the conditional labor demand
for the profit-maximizing supply:
L^*(w\ |\ p) = L^c(q^*(p\ |\ w))
L^c(q) = {1 \over 32} q^2
= {1 \over 32}\left(16p \over w\right)^2
= 8\left(p \over w\right)^2
The profit-maximizing labor demand is
Edge Cases
Edge Case 1:
Multiple quantities where P = MC
Edge Case 2:
Corner solution at \(q = 0\)
"The supply curve is the portion of the MC curve above minimum average variable cost"
Other Edge Cases to
Watch Out for On Exams
- Discontinuities
- Capacity constraints
- Quantities produced with capital
- Don't just trust formulas —
perform a gut check!
Summary
A competitive firm takes input prices \(w\) and \(r\), and the output price \(p\), as given.
We can therefore characterize its optimal choices of inputs and outputs
as functions of those prices: the supply of output \(q^*(p\ |\ w)\),
and the demand for inputs (e.g. \(L^*(w\ |\ p)\)).
We can find the optimal input-output combination either by finding the optimal quantity of output and determining the inputs required to produce it, or to find the profit-maximizing inputs and determine the resulting output. These two methods are equivalent.
Profit is increasing when marginal revenue is greater than marginal cost, and vice versa.
In most cases, the profit-maximizing choice occurs where \(MR = MC\).
If \(p\) is below the minimum value of AVC, the profit-maximizing choice is \(q = 0\).
In which MR or MC is discontinuous, logic must be applied. (There is an old exam question on the homework that explores this...and this kind of thing often shows up on exams...)
Econ 50 | Lecture 19
By Chris Makler
Econ 50 | Lecture 19
Output Supply and Labor Demand for a Competitive Firm
