基礎演算法
跟一些有的沒的
自學資源
- USACO Guide
- 校內培訓講義
- 這份簡報題目都有照難度排,可以自己選一些想
複雜度複習
int n;
cin >> n;
long long ans = 0;
for (long long i=1; i <= n; i++){
ans += i;
}
cout << ans;int n;
cin >> n;
long long ans = 0;
for (long long i=1; i <= n; i++){
ans += i;
}
cout << ans;\(O(n)\)
int n;
cin >> n;
long long ans = n*(n+1)/2;
cout << ans;int n;
cin >> n;
long long ans = n*(n+1)/2;
cout << ans;\(O(1)\)
long long n, count = 0, five = 5;
cin >> n;
while (five <= n){
count += n/five;
five *= 5;
}
cout << count;long long n, count = 0, five = 5;
cin >> n;
while (five <= n){
count += n/five;
five *= 5;
}
cout << count;\(O(log n)\)
競賽上的應用
電腦一秒鐘大約可以跑\(10^8\)~\(10^9\)次運算,所以可以大致估算運行時間。
| 範圍 | 對應的複雜度 |
|---|---|
| n < 10 | O(n!) |
| n < 20 | O(2^n) |
| n < 500 | O(n^3) |
| n < 5000 | O(n^2) |
| n < 1e5 | O(nlogn) |
| n < 1e6 | O(n) |
| n < 1e18 | O(logn) |
slides.com 不讓我在表格打Latex QQ
然後等一下就會知道為什麼有這麼多log了
演算法/資料結構
這兩個是什麼東西
演算法(Algorithm)就是一系列指揮電腦做事的步驟。它會得到一些資訊(輸入),執行一些步驟,最後會輸出結果。
資料結構(Data Structure) 則是在電腦中儲存東西的方式,像是上個禮拜講的所有東西。
在比賽中,考驗的就是你設計出好的演算法的能力,過程中會應用到許多資料結構。
排序
看得出來它在幹嘛嗎
看得出來它在幹嘛嗎
int n;
cin >> n;
vector<int> arr(n);
for(int i = 0; i < n; i++) cin >> arr[i];
for(int i = 0; i < n; i++){
int mini = arr[i], min_pos = i;
for(int j = i; j < n; j++){
if(arr[j] < mini){
mini = arr[j];
min_pos = j;
}
}
swap(arr[min_pos], arr[i]);
}複雜度?
看得出來它在幹嘛嗎
int n;
cin >> n;
vector<int> arr(n);
for(int i = 0; i < n; i++) cin >> arr[i];
for(int i = 0; i < n; i++){
int mini = arr[i], min_pos = i;
for(int j = i; j < n; j++){
if(arr[j] < mini){
mini = arr[j];
min_pos = j;
}
}
swap(arr[min_pos], arr[i]);
}複雜度?
\(O(n^2)\)
這樣好像太慢欸
一樣想一下它在做什麼
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5 6
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5 6 7
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5 6 7 7
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5 6 7 7 8
Merge sort
把兩個排序好的陣列合併?
| 1 | 4 | 5 | 7 | 8 | 10 |
|---|
| 2 | 3 | 6 | 7 | 9 | 12 |
|---|
1 2 3 4 5 6 7 7 8 9 10 12
Merge sort
排序好的陣列哪裡來?
Merge sort
排序好的陣列哪裡來?

Merge sort
仔細看圖可以發現複雜度變成了\(O(nlogn)\)
實作上會使用遞迴的技巧:先將左右兩區間遞迴處理,再將兩區間合併。
Merge sort
#include<iostream>
#include<vector>
using namespace std;
vector<int> vec;
void merge(int l, int r){
if(l == r) return;
int mid = (l + r) / 2;
merge(l, mid);
merge(mid + 1, r); //分兩邊遞迴
int i = l, j = mid + 1; // i為第一個陣列 j為第二個
vector<int> tmp;
while(i <= mid && j <= r){
if(vec[i] < vec[j]){
tmp.push_back(vec[i]);
i++;
}
else{
tmp.push_back(vec[j]);
j++;
}
}
while(i <= mid) tmp.push_back(vec[i]), i++;
while(j <= r) tmp.push_back(vec[j]), j++;
for(int k = l; k <= r; k++){
vec[k] = tmp[k-l];
}
return;
}
int main(){
int n;
cin >> n;
vec.resize(n);
for(int i = 0; i < n; i++){
cin >> vec[i];
}
merge(0, n - 1);
for(int i = 0; i < n; i++){
cout << vec[i] << " ";
}
}內建函式
每次想排序都要寫一長串太麻煩了,可以用#include<algorithm>裡頭的sort
int N = 1e5;
int arr[N];
for(int i=0; i < N; i++) cin >> arr[i];
sort(arr, arr + N);
for(int i=0; i < N; i++) cout << arr[i];內建函式
vector版
int N = 1e5;
vector<int> vec(N);
for(int i=0; i < N; i++) cin >> vec[i];
sort(vec.begin(), vec.end());
for(int i=0; i < N; i++) cout << vec[i];內建函式
從大排到小
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 1e5 + 5;
int n;
int a[SIZE];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
sort (a + 1, a + n + 1, greater<int>());
for (int i = 1; i <= n; i++) cout << a[i] << " \n";
}
內建函式
可以自己定義排序條件
在這裡是將數字照除以k的餘數排序
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 1e5 + 5;
int n, k;
int a[SIZE];
// 自訂比較函式
bool cmp (int x, int y) {
int mx = x % k, my = y % k;
if (mx != my) return mx > my;
return x < y;
}
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
sort (a + 1, a + n + 1, cmp);
for (int i = 1; i <= n; i++) cout << a[i] << " \n";
}內建函式
也可以使用lambda
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 1e5 + 5;
int n, k;
int a[SIZE];
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
sort (a + 1, a + n + 1, [] (int x, int y) {
int mx = x % k, my = y % k;
return mx != my ? mx > my : x < y;
});
for (int i = 1; i <= n; i++) cout << a[i] << " \n";
}
例題
給定一個有\(N\)個數字的序列\(A\),計算有幾對數對\((i,j)\)使得\(i<j\)且\(a_i>a_j\)
\(N<10^5\)
給定一個有\(N\)個數字的序列\(A\),計算有幾對數對\((i,j)\)使得\(i<j\)且\(a_i>a_j\)
\(N<10^5\)
還記得Merge Sort嗎?我們可以在合併兩個陣列的時候順便計算逆序數對的數量。複雜度\(O(nlogn)\)
Code待補
#include<iostream>
#include<vector>
#define int long long
using namespace std;
vector<int> vec;
int merge(int l, int r){
if(l == r) return 0;
int mid = (l + r) / 2, ans=0;
ans += merge(l, mid);
ans += merge(mid + 1, r); //分兩邊遞迴
int i = l, j = mid + 1; // i為第一個陣列 j為第二個
vector<int> tmp;
while(i <= mid && j <= r){
if(vec[i] <= vec[j]){
tmp.push_back(vec[i]);
i++;
}
else{
tmp.push_back(vec[j]);
ans += mid - i + 1;
j++;
}
}
while(i <= mid) tmp.push_back(vec[i]), i++;
while(j <= r) tmp.push_back(vec[j]), j++;
for(int k = l; k <= r; k++){
vec[k] = tmp[k-l];
}
return ans;
}
signed main(){
int n;
int cnt = 1;
while(cin >> n){
if(n == 0) break;
vector<int> tmp(0);
swap(vec,tmp);
vec.resize(n);
for(int i = 0; i < n; i++){
cin >> vec[i];
}
cout << "Case #"<< cnt++ << ": "<< merge(0, n - 1) << "\n";
}
}題目
枚舉
枚舉
就是暴力的意思。
教這個幹嘛?
枚舉
就是暴力的意思。
教這個幹嘛?

類似第一子題的概念。
很多時候也可以用暴力來驗證解答或想法
遞迴枚舉
有時候你需要枚舉\(\binom{n}{k}\)種從n個東西中取k個的方法,可是沒辦法寫n層迴圈。
這時我們就又需要遞迴的幫助。在程式中我們會順便紀錄現在取到第幾個數字,當取完就中止遞迴。
遞迴枚舉
#include<iostream>
#include<vector>
using namespace std;
vector<int> cur;
void solve(int n, int k, int cur_n, int cur_k){
if(n+1 == cur_n && k == cur_k){
for(int i=0; i<k; i++){
cout << cur[i] << " ";
}
cout << "\n";
return;
}
if(n+1 == cur_n){
//沒取滿k個,直接終止程式
return;
}
if(cur_k < k){
//取當前數字
cur.push_back(cur_n);
solve(n, k, cur_n + 1, cur_k + 1);
cur.pop_back(); //很重要!記得拿出來
}
//不取當前數字
solve(n, k, cur_n + 1, cur_k);
}
int main(){
int n,k;
cin >> n >> k;
solve(n, k, 1, 0);
}0/1 枚舉
有一些東西,你想要取其中一些算答案。
還是可以遞迴,只是比較難寫。
0/1 枚舉
有一些東西,你想要取其中一些算答案。
還是可以遞迴,只是比較難寫。
每個元素都是取(1)或不取(0),是不是可以寫成二進位?
0/1 枚舉
有一些東西,你想要取其中一些算答案。
還是可以遞迴,只是比較難寫。
每個元素都是取(1)或不取(0),是不是可以寫成二進位?
所以可以從\(1\)枚舉到\(2^n-1\),如果二進位的第\(i\)位是\(1\),則代表要取這個數字。
排列枚舉
顧名思義就是要枚舉所有排列
這裡可以用C++內建的next_permutation
接下來會用題目講解每種枚舉的寫法
有一個西洋棋棋盤,你想要在上面放\(8\)個皇后,使得皇后都不互相攻擊別人。棋盤上有些格子是髒的,不能放皇后。問有幾種可能的排法。
遞迴枚舉!可是\(\binom{64}{8}\)超大,會TLE
遞迴枚舉!可是\(\binom{64}{8}\)超大,會TLE
為了加快速度,可以ㄧ發現同一行有兩個皇后就中止遞迴。這種方法叫做剪枝。
有\(N\)顆蘋果,你想把它分成兩堆,使得兩邊重量差距最小。
\(N<20\)
就是剛剛的0/1枚舉
#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;
int main(){
int n;
cin >> n;
vector<ll> vec(n);
for(int i = 0; i < n; i++) cin >> vec[i];
ll ans = 1e18;
for(int i = 0; i < (1 << n); i++){
ll a = 0, b = 0;
for(int j = 0; j < n; j++){
if(i & (1 << j)){
a += vec[j];
}
else{
b += vec[j];
}
}
ans = min(ans, llabs(a - b));
}
cout << ans;
}給一個長度為\(N\)的字串,照字典序輸出所有重組完可能出現的字串
\(N<8\)
利用next_permutation (記得要先排序!)
#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
using namespace std;
int main(){
string s;
cin >> s;
sort(s.begin(), s.end());
vector<string> vec;
int count=0;
do{
count++;
vec.push_back(s);
}while(next_permutation(s.begin(), s.end()));
cout << count << "\n";
for(auto i:vec){
cout << i << "\n";
}
}
聰明的枚舉
聰明的枚舉
有時候只需要枚舉一部分東西,就能計算答案了
例:給\(N\),請因式分解\(N\)
\(N\leq10^8\)
聰明的枚舉
有時候只需要枚舉一部分東西,就能計算答案了
例:給\(N\),請因式分解\(N\)
\(N\leq10^8\)
枚舉\(2\)~\(\sqrt{N}\)就行了!剩下來的那個數字一定是質數。
聰明的枚舉
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
bool f = 0; // 之前是否有輸出數字
for (int i = 2, sq = sqrt (n); i <= sq; i++) { // sqrt (n) 在一開始先計算好,避免大量的 sqrt 運算
int cnt = 0;
while (n % i == 0) {
cnt++;
n /= i;
}
if (cnt > 0) {
if (f == 0) f = 1;
else cout << " * ";
if (cnt == 1) cout << i;
else cout << i << '^' << cnt;
}
}
if (n > 1) {
if (f == 1) cout << " * ";
cout << n;
}
cout << '\n';
}
題目
提示:\(\sum_{i=1}^N \frac{N}{i} \simeq NlogN\)
二分搜
老到牙的遊戲
我現在心裡在想一個數字\(N\),你可以猜數字,我會跟你講比較大還是比較小。
老到牙的遊戲
我現在心裡在想一個數字\(N\),你可以猜數字,我會跟你講比較大還是比較小。
大家的直覺應該都會切一半吧。這就是所謂的二分搜,因為每次範圍都會變一半,所以只要猜\(O(logN)\)次就猜的中了。
老到牙的遊戲
我現在心裡在想一個數字\(N\),你可以猜數字,我會跟你講比較大還是比較小。
大家的直覺應該都會切一半吧。這就是所謂的二分搜,因為每次範圍都會變一半,所以只要猜\(O(logN)\)次就猜的中了。
有時候你只能驗證答案可不可行,不能直接算出來,這時候就可以仰賴二分搜。
一些範例
有一些數字,我想要找出裡面第一個比\(x\)大的。
一些範例
有一些數字,我想要找出裡面第一個比\(x\)大的。
把陣列排序好之後就可以二分搜了。
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int main(){
int n, x;
cin >> n >> x;
vector<int> vec(n);
for(int i = 0; i < n; i++){
cin >> vec[i];
}
sort(vec.begin(), vec.end());
int l = 0, r = n - 1; //答案有可能在[l,r]
while(l < r){
int mid = (l + r) / 2;
if(vec[mid] >= x){
r = mid;
}
else{
l = mid + 1;
}
}
cout << l + 1;
}
debug
程式在空轉?可以思考一下等號成立時會發生什麼事,並用此推測要讓\(r=mid\)還是\(r=mid-1\),要讓\(l=mid\)還是\(l=mid+1\)
\(mid\)的選法可能也有影響,
跑不動可以換成\(\frac{l+r}{2}+1\)試試看
debug
如果\(l\)跟\(r\)有可能是負數,那有可能被c++的奇怪除法卡到。
這時可以把\(mid=\frac{l+r}{2}\)改為\(mid=l+\frac{r-l}{2}\)
最後要很小心overflow的問題。
內建函式
剛剛的程式也可以用內建函式取代,記得還是要sort
vector<int> vec = {5, 4, 9, 10, 2};
sort(vec.begin(), vec.end());
int lb = lower_bound(vec.begin(), vec.end(), 9) - vec.begin(); //第一個>=x的
int rb = upper_bound(vec.begin(), vec.end(), 9) - vec.begin(); //第一個>x的
set<int> s = {5, 4, 9, 10, 2};
set<int>::iterator lb = s.lower_bound(9); // set記得要用這個,不然複雜度會退化。然後set不能知道是第幾大,只能知道數字大小浮點數上二分搜
可以設定一個很小的數字,如果r-l比它小就跳出
double eps = 1e-6;
double l = 0, r = 1e9;
while(r - l > eps){
//do something
}對答案二分搜
什麼時候需要自己寫二分搜呢?
對答案二分搜
什麼時候需要自己寫二分搜呢?
題目問你最大(小)的答案是多少時,如果只要比答案小(大)都符合題目條件,就可以使用二分搜。
二分搜的題目也有一個特點:很容易確認符不符合條件,但不能直接算出答案。
例題
有\(N\)臺機器,第\(i\)臺機器做一個產品要花\(k_i\)秒,機器可以同時運作。最少要花幾秒才能做完\(t\)個產品?
\(N<2*10^5\)
假如\(x\)秒做得完,那\(x+1\)秒也做得完,所以可以用二分搜。
假如\(x\)秒做得完,那\(x+1\)秒也做得完,所以可以用二分搜。
要怎麼知道\(x\)秒做不做得完?
#include<iostream>
#include<vector>
#include<algorithm>
#define ll long long
using namespace std;
int main(){
ll n, t;
cin >> n >> t;
vector<ll> vec(n);
for(int i = 0; i < n; i++) cin >> vec[i];
ll l = 1,r = 1e18;
while(l<r){
ll mid = (l + r) >> 1,sum = t;
for(auto x:vec){
sum -= mid / x;
if(sum < 0) break;
}
if(sum <= 0) r = mid;
else l = mid + 1;
}
cout << l;
}題目
三分搜
三分搜
跟二分搜差不多,蠻少用到的。
是用來在二次函數那樣的函數找最小(大)值
三分搜
跟二分搜差不多,蠻少用到的。
是用來在二次函數那樣的函數找最小(大)值
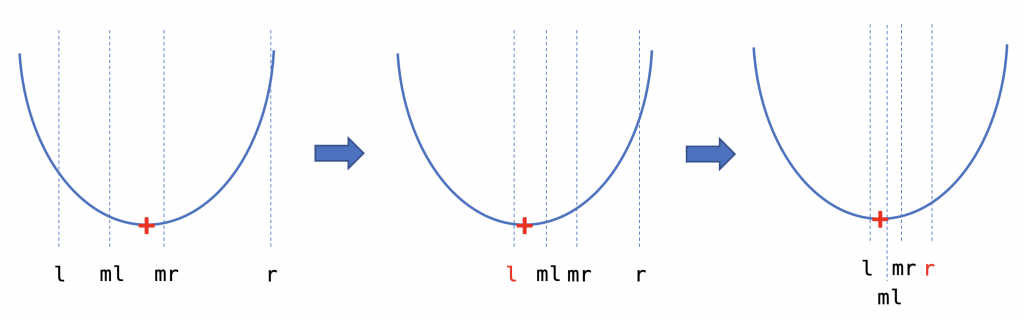
題目
分治
分治
還記得Merge Sort嗎?
Merge Sort 大致可以分成三個部分:
Divide:把大問題切成小問題
Conquer:把小問題遞迴,解決
Merge:將兩個解決後的小問題合併
分治
這個思想其實可以用在非常多地方,常用到以後每堂課它都會不停地出現。
今天會講解一些例題,讓你了解分治的概念。
以後的其他課會學到更多用到分治的演算法。
例題
平面上有\(N\)個點,請找出最近的兩個點
\(N\leq2*10^5\)
沿用分治的思想,把平面切成兩半。
沿用分治的思想,把平面切成兩半。
那這樣答案會是\(min(left, right, middle)\)
沿用分治的思想,把平面切成兩半。
那這樣答案會是\(min(\)左,右,左右之間\()\)
左邊跟右邊可以遞迴下去算,啊橫跨中間的呢?
沿用分治的思想,把平面切成兩半。
那這樣答案會是\(min(\)左,右,左右之間\()\)
左邊跟右邊可以遞迴下去算,啊橫跨中間的呢?

會不會全部的點都在裡面,這樣複雜度還是\(O(n^2)\)?

可以照y座標排序,檢查相鄰的八個點就好!
複雜度\(O(nlog^2n)\)

複雜度怎麼算?
分治的複雜度很玄學,可以用主定理(Master Theorem)計算,但是講師不會,有興趣的可以自己看看。(或是如果有剩時間可以一起研究)
複雜度怎麼算?
分治的複雜度很玄學,可以用主定理(Master Theorem)計算,但是講師不會,有興趣的可以自己看看。(或是如果有剩時間可以一起研究)
比較簡單的方法是把遞迴的圖畫出來,像之前Merge Sort一樣,再來看做了幾次運算。
給定\(a,b\),請計算\(a^b\) mod \(10^9+7\)
\(a,b\leq10^9\)
直接用迴圈算?
\(O(b)\), TLE
假設b是偶數
一樣沿用分治的思想,把\(a^b\)變成\((a^{b/2})^{2}\)。
那就先把\(a^{b/2}\)算出來,再自己乘自己就好了。
b是奇數?
假設b是偶數
一樣沿用分治的思想,把\(a^b\)變成\((a^{b/2})^{2}\)。
那就先把\(a^{b/2}\)算出來,再自己乘自己就好了。
b是奇數?
變成\(a^{b/2}*a^{b/2}*a\)
假設b是偶數
一樣沿用分治的思想,把\(a^b\)變成\((a^{b/2})^{2}\)。
那就先把\(a^{b/2}\)算出來,再自己乘自己就好了。
b是奇數?
變成\(a^{b/2}*a^{b/2}*a\)
複雜度?
假設b是偶數
一樣沿用分治的思想,把\(a^b\)變成\((a^{b/2})^{2}\)。
那就先把\(a^{b/2}\)算出來,再自己乘自己就好了。
b是奇數?
變成\(a^{b/2}*a^{b/2}*a\)
複雜度?
\(O(logb)\)
#include<iostream>
#define int long long
using namespace std;
const int modulo = 1e9+7;
int power(int a, int b){
if(b == 0) return 1;
else if(b % 2 == 1) return (a * power(a, b - 1)) % modulo;
else{
int tmp=power(a, b / 2);
return tmp * tmp % modulo;
}
}
signed main(){
int n;
cin >> n;
int a, b;
for(int i = 0; i< n; i++){
cin >> a >> b;
cout << power(a, b) << "\n";
}
return 0;
}題目
雙指標
有一個長度為\(N\)的陣列,請找出兩個數字使得它們加起來是\(x\)
\(N\leq2*10^5\)
\(x\leq10^9\)
不會?把陣列排序看看
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
再放兩個指標
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
再放兩個指標
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
\(2+10<14\)
再放兩個指標
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
\(3+10<14\)
再放兩個指標
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
\(5+10>14\)
再放兩個指標
| 2 | 3 | 5 | 6 | 9 | 10 |
|---|
\(x=14\)
\(5+9=14\)
雙指標
這就是雙指標最基本的應用。
雙指標的特性:陣列遵守某種單調性時(在這裡是由小到大),可以用兩個指標去搜索。因為指標只會從左走到右(或右到左)一次,所以複雜度是\(O(n)\)
還記得Merge Sort嗎?合併的過程就是雙指標的一種。
題目
會用到DP的概念,不知道可以跳過
前綴和
前綴和
就是把前綴全部加起來。
| 1 | 5 | 2 | 3 | 1 | 2 |
|---|
前綴和
就是把前綴全部加起來。
| 1 | 5 | 2 | 3 | 1 | 2 |
|---|
| 1 | 6 | 8 | 11 | 12 | 14 |
|---|
前綴和
這可以拿來幹嘛?
| 1 | 5 | 2 | 3 | 1 | 2 |
|---|
| 1 | 6 | 8 | 11 | 12 | 14 |
|---|
前綴和
這可以拿來幹嘛?
| 1 | 5 | 2 | 3 | 1 | 2 |
|---|
| 1 | 6 | 8 | 11 | 12 | 14 |
|---|
我想要知道\(a_2+a_3+a_4+a_5\)
本來要一個一個加起來,但有了前綴和?
前綴和
這可以拿來幹嘛?
| 1 | 5 | 2 | 3 | 1 | 2 |
|---|
| 1 | 6 | 8 | 11 | 12 | 14 |
|---|
我想要知道\(a_2+a_3+a_4+a_5\)
本來要一個一個加起來,但有了前綴和?
\(\sum_{i=c}^d{a_i} = pref_d - pref_{c-1}\)
例題
給一個長度為\(N\)的陣列,接著有\(Q\)筆詢問,問一段子陣列[a,b]的和
\(N,Q\leq2*10^5\)
建造前綴和陣列,就可以用一次減法回答一個詢問
#include<iostream>
#include<vector>
#define ll long long
using namespace std;
int main(){
int n, q;
cin >> n >> q;
vector<int> vec(n+1);
for(int i = 1; i <= n; i++) cin >> vec[i];
vector<int> pre(n+1);
for(int i = 1; i <= n; i++) pre[i] = pre[i-1] + vec[i];
int a, b;
for(int i = 0; i < q; i++){
cin >> a >> b;
cout << pre[b] - pre[a-1] << "\n";
}
}給一個長度為\(N\)的陣列,請求出最大區間和
\(N\leq2*10^5\)
蓋了前綴和陣列後,問題變成:
讓\(pref_r\)盡量最大,\(pref_l\)盡量最小
蓋了前綴和陣列後,問題變成:
讓\(pref_r\)盡量最大,\(pref_l\)盡量最小
那就用一個變數\(mini\)記錄目前以來最小的值!
#include<iostream>
#include<vector>
#include<algorithm>
#define int long long
using namespace std;
signed main(){
int n;
cin >> n;
vector<int> vec(n+1);
for(int i = 1; i <= n; i++) cin >> vec[i];
vector<int> pre(n+1);
for(int i = 1; i <= n; i++) pre[i] = vec[i] + pre[i-1];
int maxi = -1e9-7, mini = 1e9+7; //maxi = 目前看到的最大區間和,mini = 目前看到最小的前綴和
for(int i = 0; i < n; i++){
mini = min(mini, pre[i]);
maxi = max(maxi, pre[i+1] - mini);
}
cout << maxi;
}題目
提示:map
基礎演算法
By ck1110530
基礎演算法
- 633



