A Brief Intro to Bayesian Analysis
From intuition to A/B testing
Cam Davidson-Pilon
Follow these slides bit.ly/nwcamdp
Bayesian inference is about preserving uncertainty
Frequentist philosophy
on what "probability" means
Probability is the frequency of some event in a long running sequence of trials
Bayesian philosophy
on what "probability" means
Probability is an individual's measure of belief an event will occur.
Probability is subjective!
1. We have different beliefs (read: assign different probabilities) of events, like political outcomes, occurring based on our information of the world.
2. We should have similar beliefs that a rolled dice will come show a 6 1/6th of the time.
Tiny Bit of Probability Notation
P(A) is called the prior probability of event A occuring
P(A|X) is called the posterior probability of event A occuring, given information X
Coin Flip Example
P(A): The coin has a 50 percent chance of being Heads.
P(A|X): You look at the coin, observe a Heads has landed, denote this information X, and trivially assign probability 1.0 to Heads and 0.0 to Tails.
Buggy Code Example
P(A): This big, complex code likely has a bug in it.
P(A|X): The code passed all X tests; there still might be a bug, but its presence is less likely now.
Medical Patient Example
P(A): The patient could have any number of diseases.
P(A|X): Performing a blood test generated evidence X, ruling out some of the possible diseases from consideration.
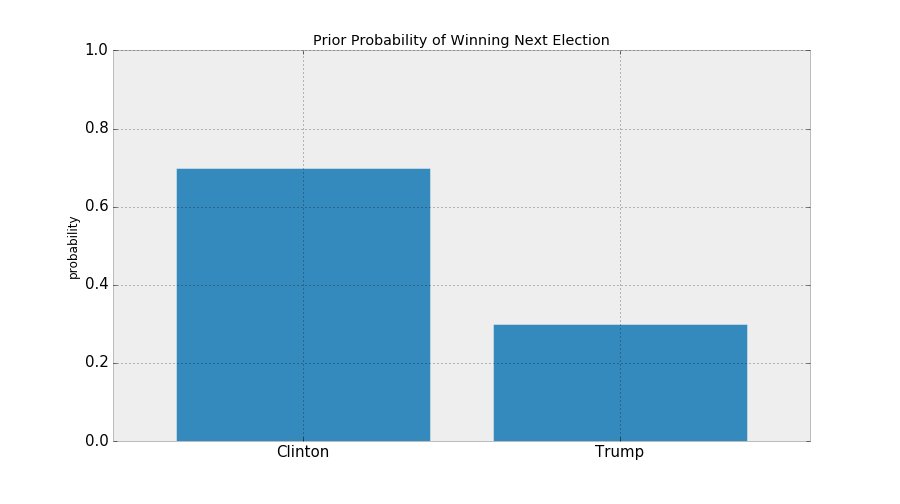
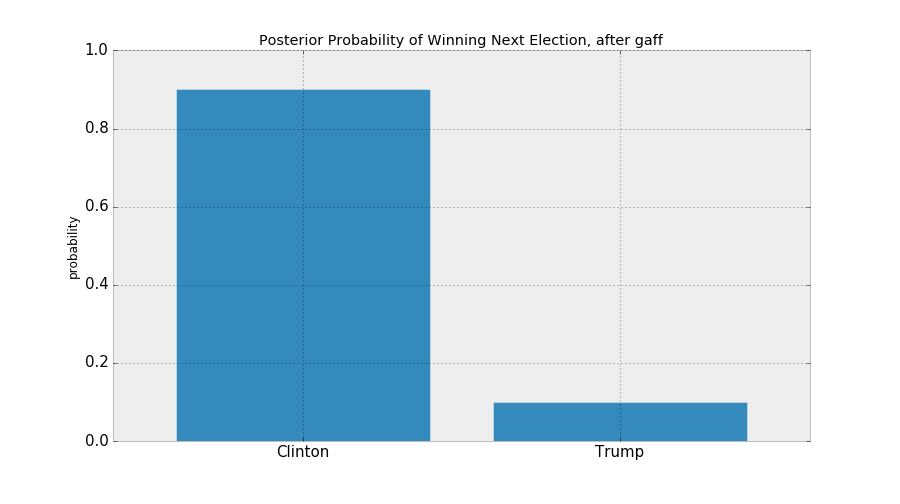
Back to Coins Again
Suppose I don't know what the frequency of heads is.
¯\_(ツ)_/¯
So I decide to start flipping a coin...
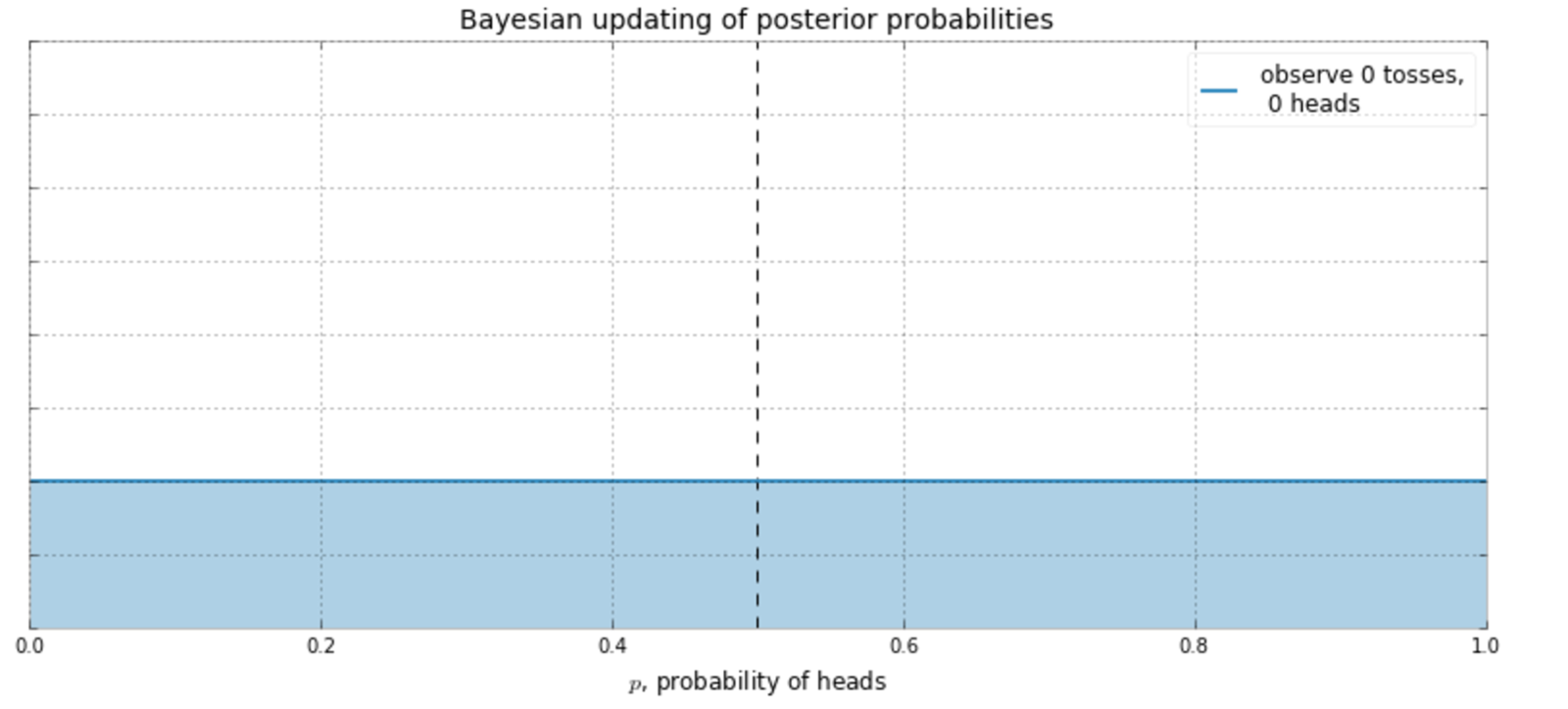
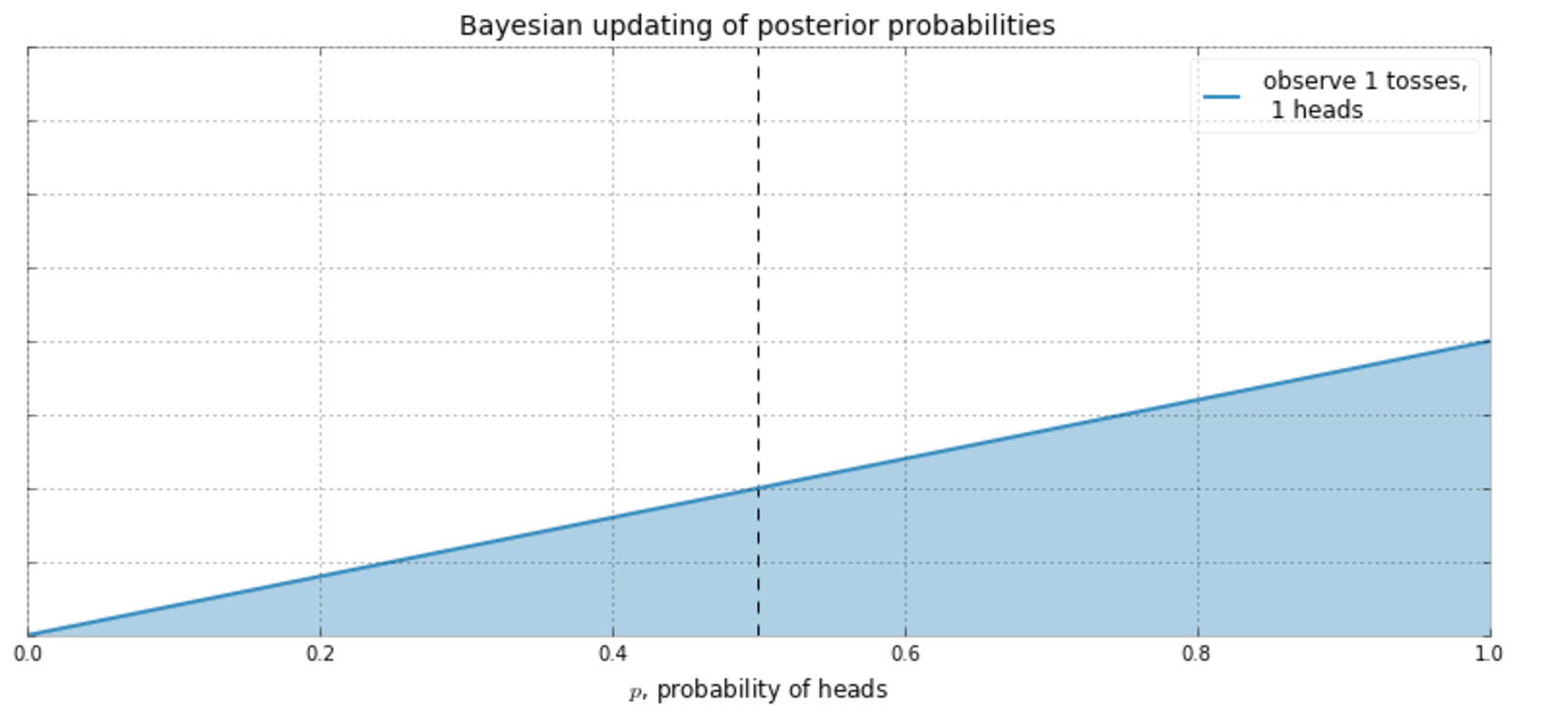
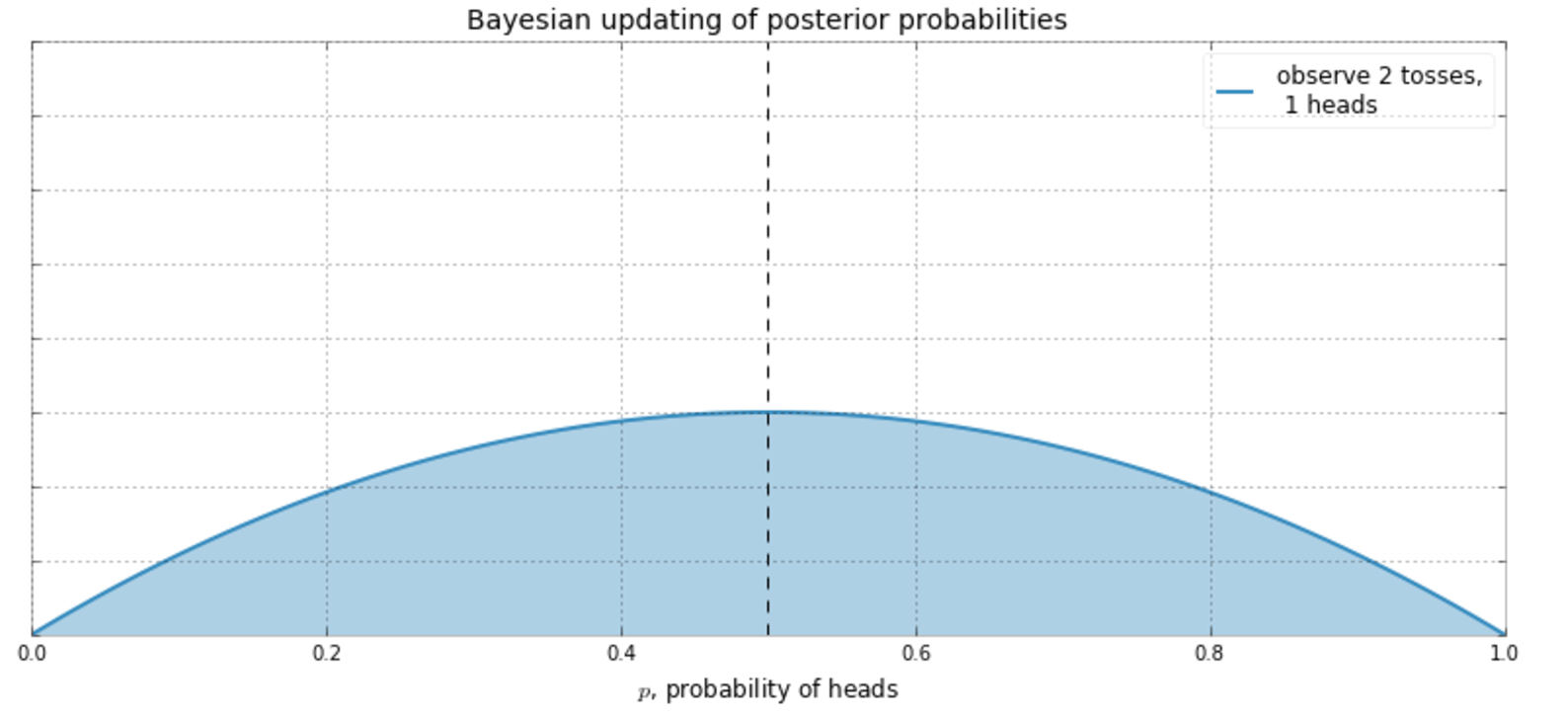
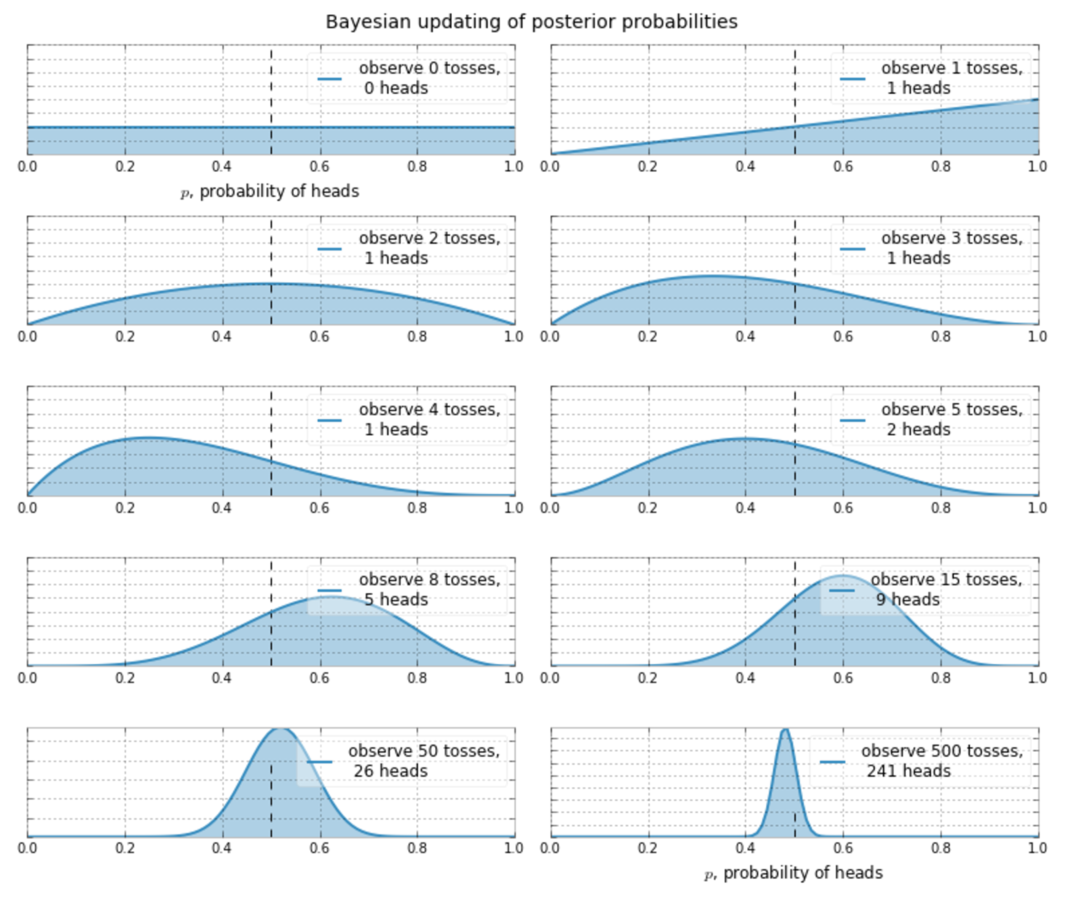
Bayesian is the opposite side of the inference coin.
Rather than be more right, we try to be less wrong.
Bayesian inference is about preserving uncertainty
C_i = \text{Poisson}(\lambda)
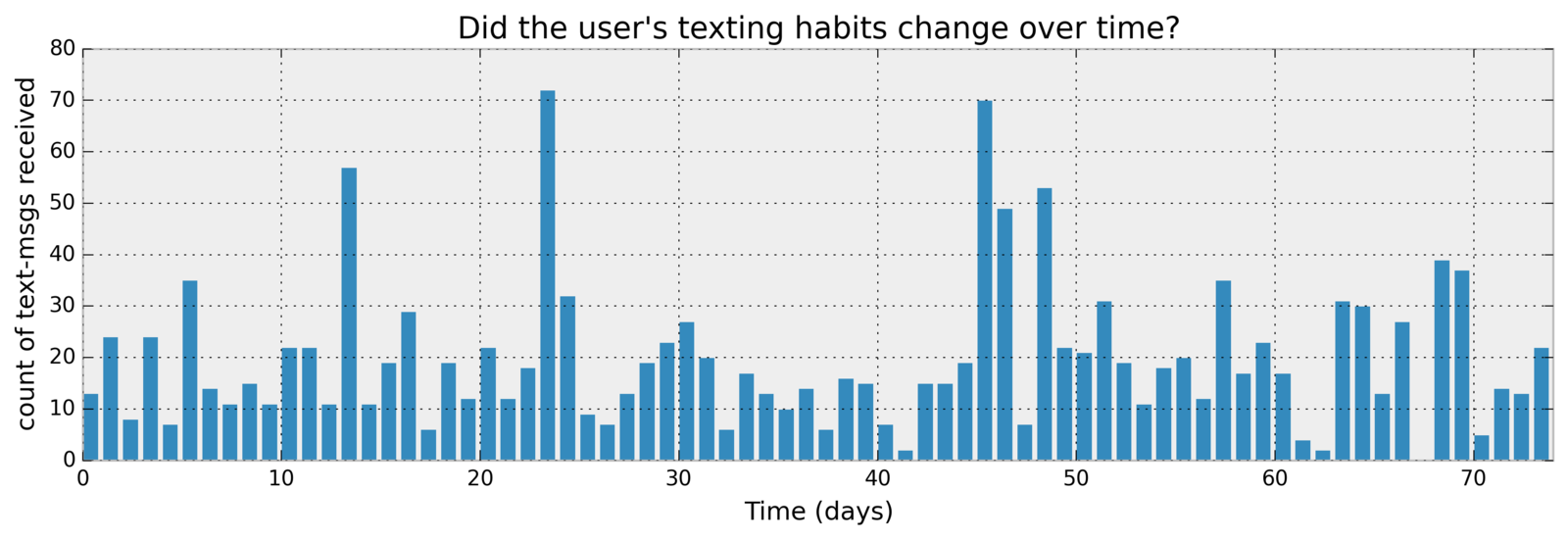
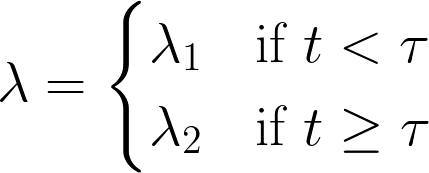
import pymc as pm
alpha = 0.5
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform('tau', 0, 75)
@pm.deterministic
def lambda_(tau=tau, lambda_1=lambda_1, lambda_2=lambda_2):
dynamic_lambdas = np.zeros(n_count_data)
dynamic_lambdas[:tau] = lambda_1 # lambda before tau is lambda1
dynamic_lambdas[tau:] = lambda_2 # lambda after (and including) tau is lambda2
return dynamic_lambdas
observations = pm.Poisson("obs", lambda_, value=count_data, observed=True)
model = pm.Model([observations, lambda_1, lambda_2, tau])
mcmc = pm.MCMC(model)
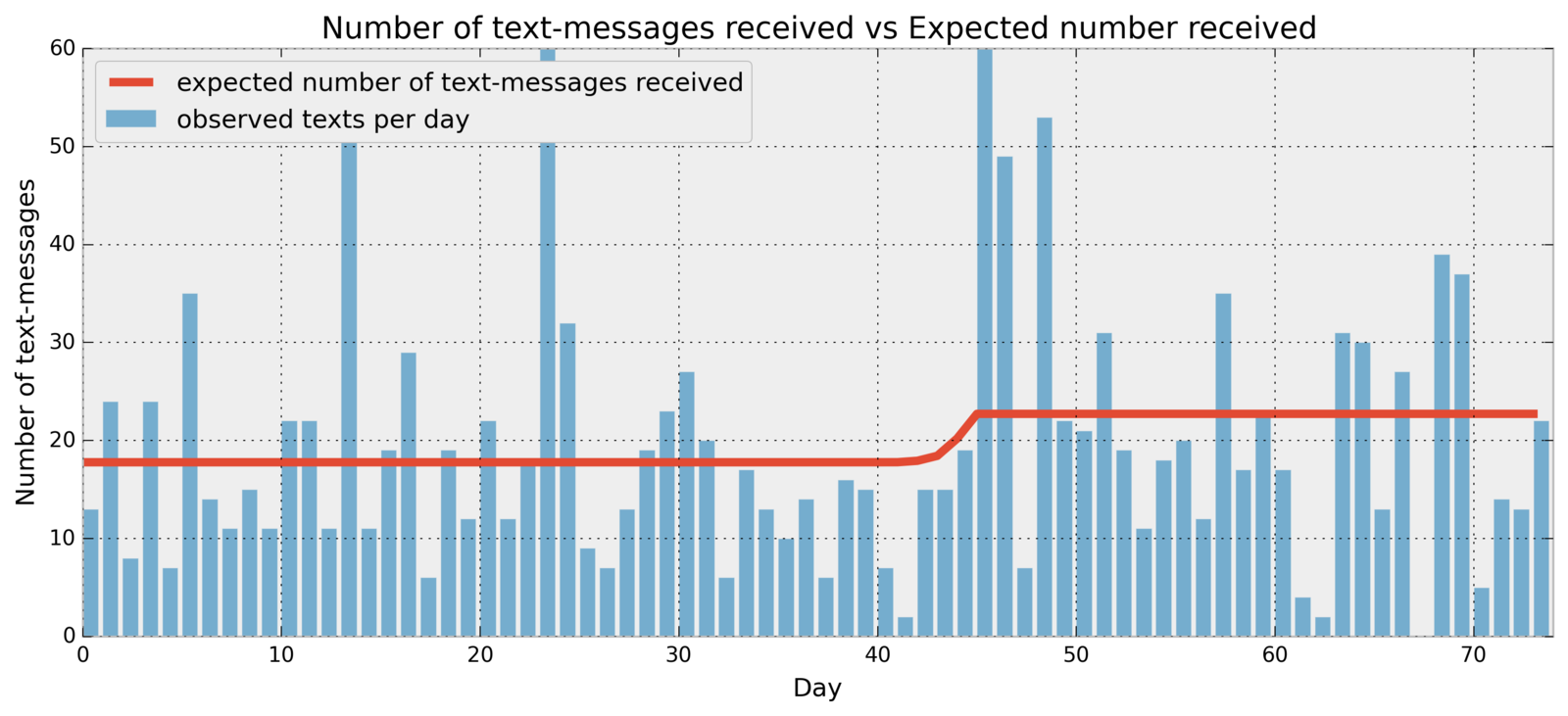
mcmc.sample(40000, 10000, 1)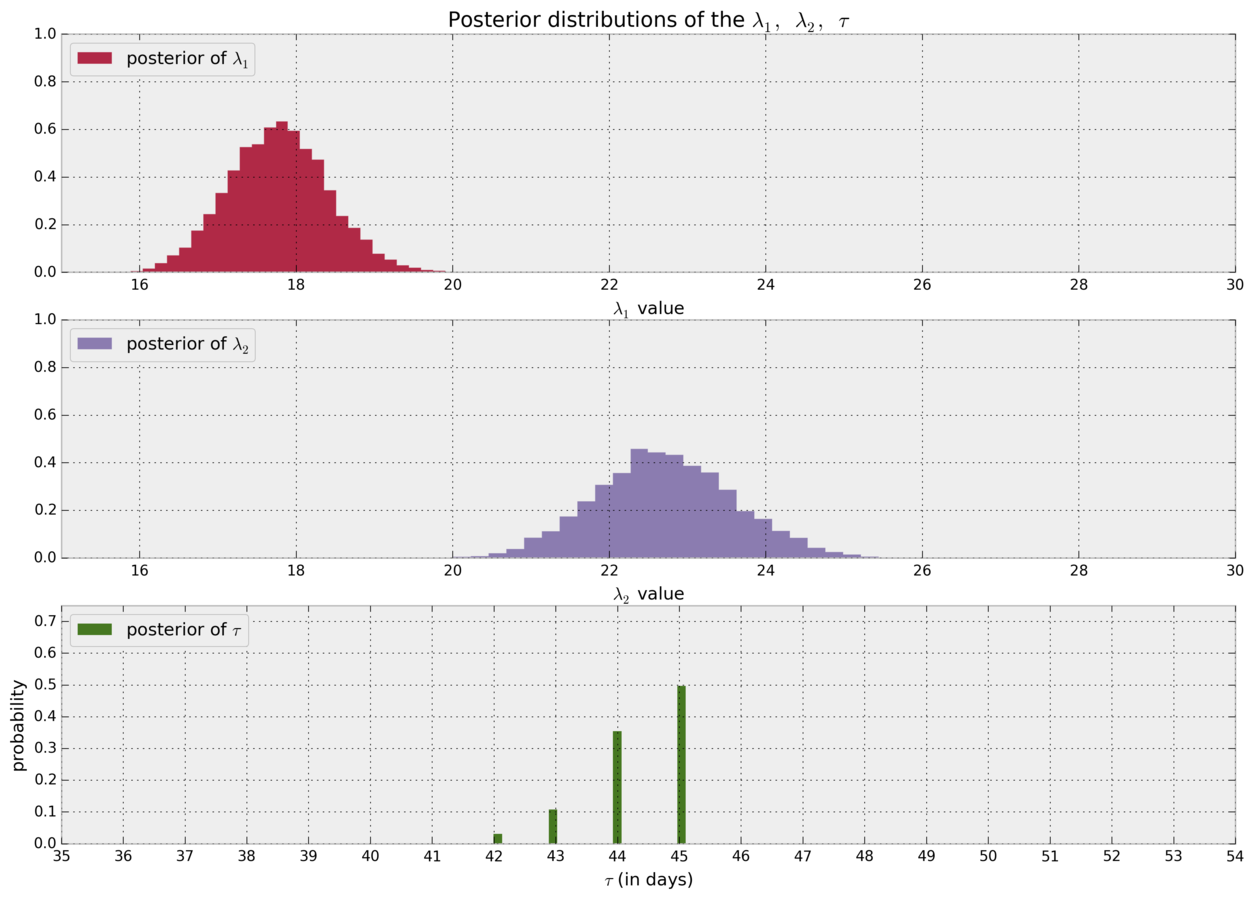
A/B Testing
Bayesian Analysis in A/B Testing
| Group | Visitors | Conversions |
|---|---|---|
| Control | ? | ? |
| Experiment | ? | ? |
Pre Experiment
| Group | Visitors | Conversions |
|---|---|---|
| Control | 2000 | 100 |
| Experiment | 2000 | 150 |
Experiment Results
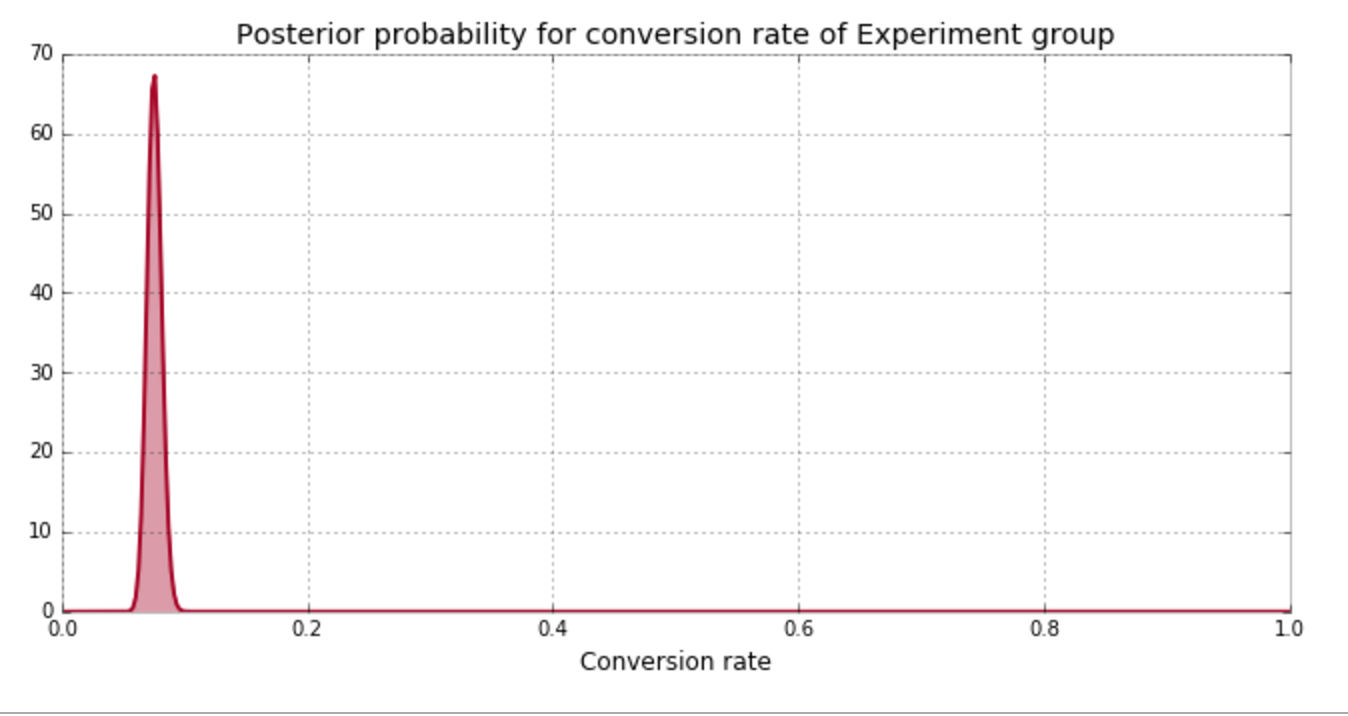
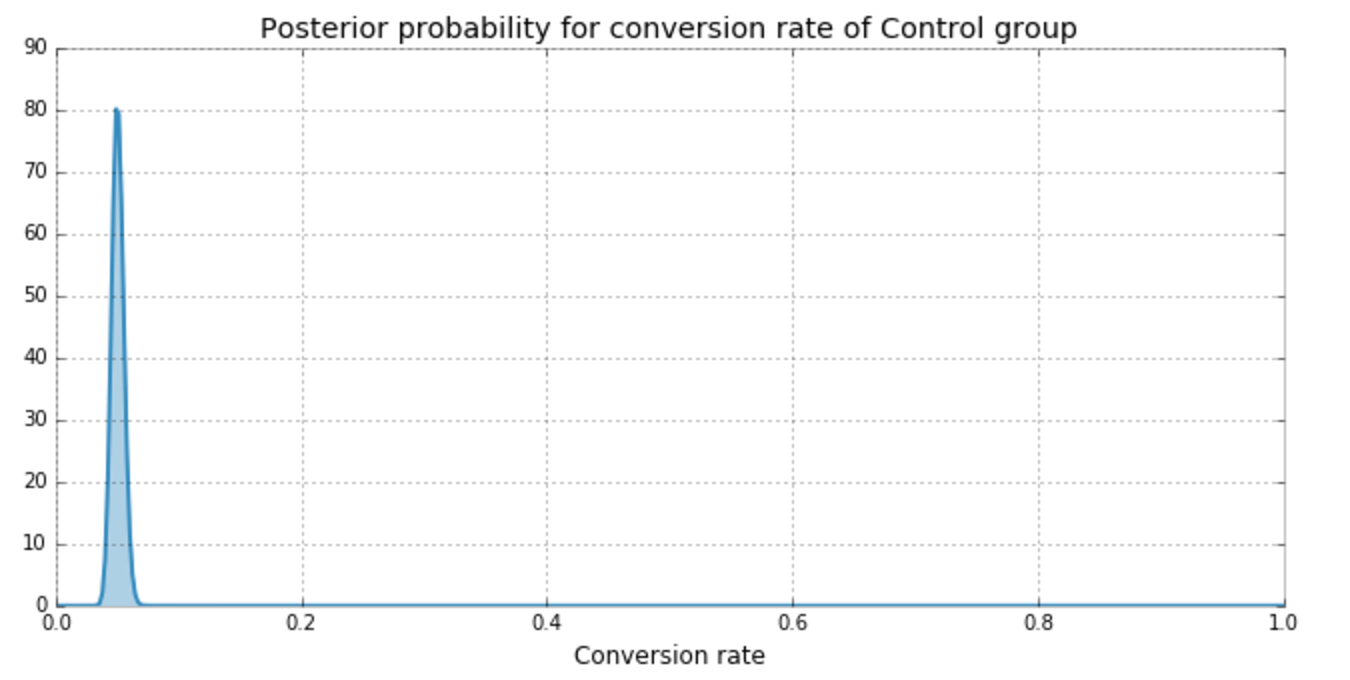
| Group | Visitors | Conversions |
|---|---|---|
| Control | 2000 | 100 |
| Experiment | 2000 | 150 |
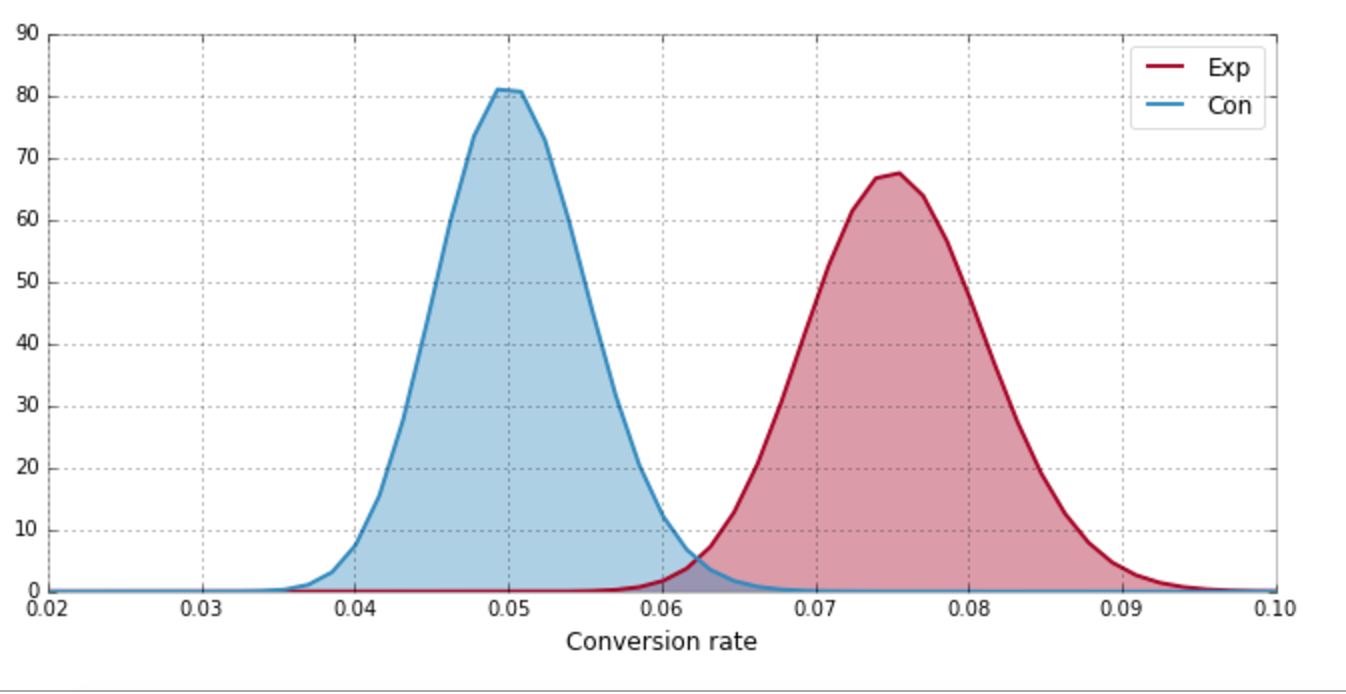
Experiment Results
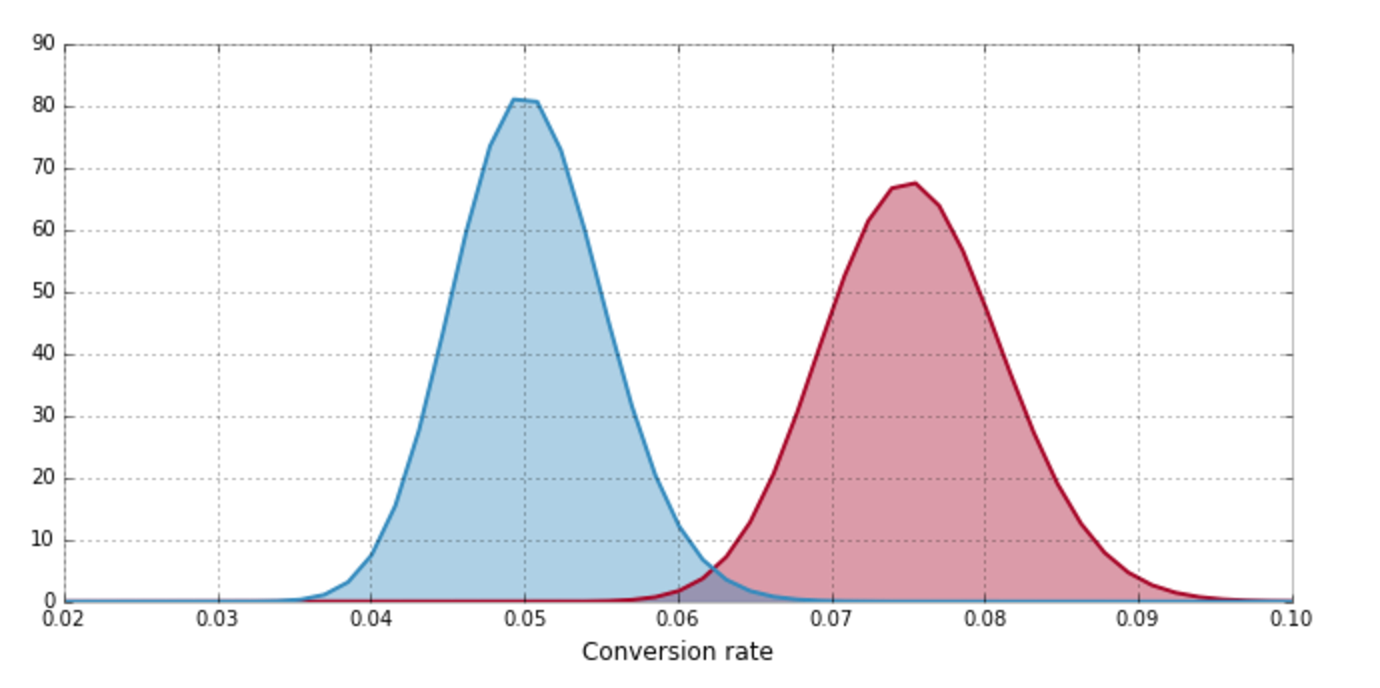
Forget Traditional P-Values
p := P(C_{\text{Exp}} > C_{\text{Con}} \;|\; \text{Data})
What the business units really want is
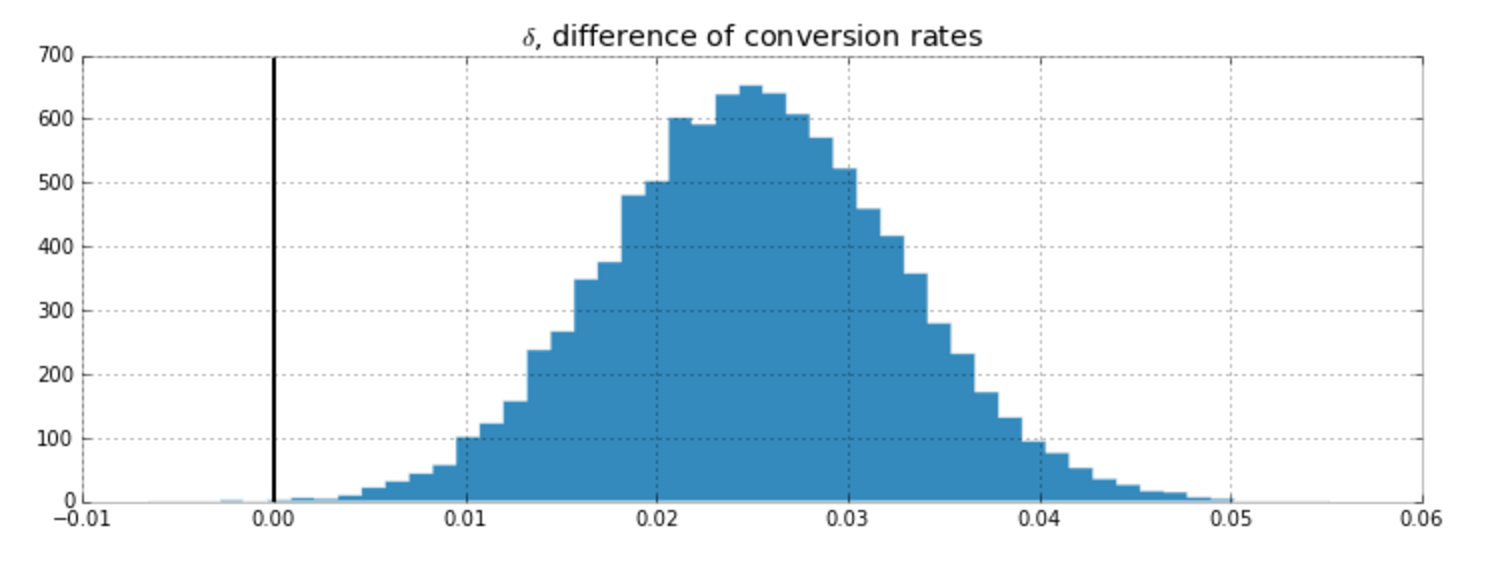
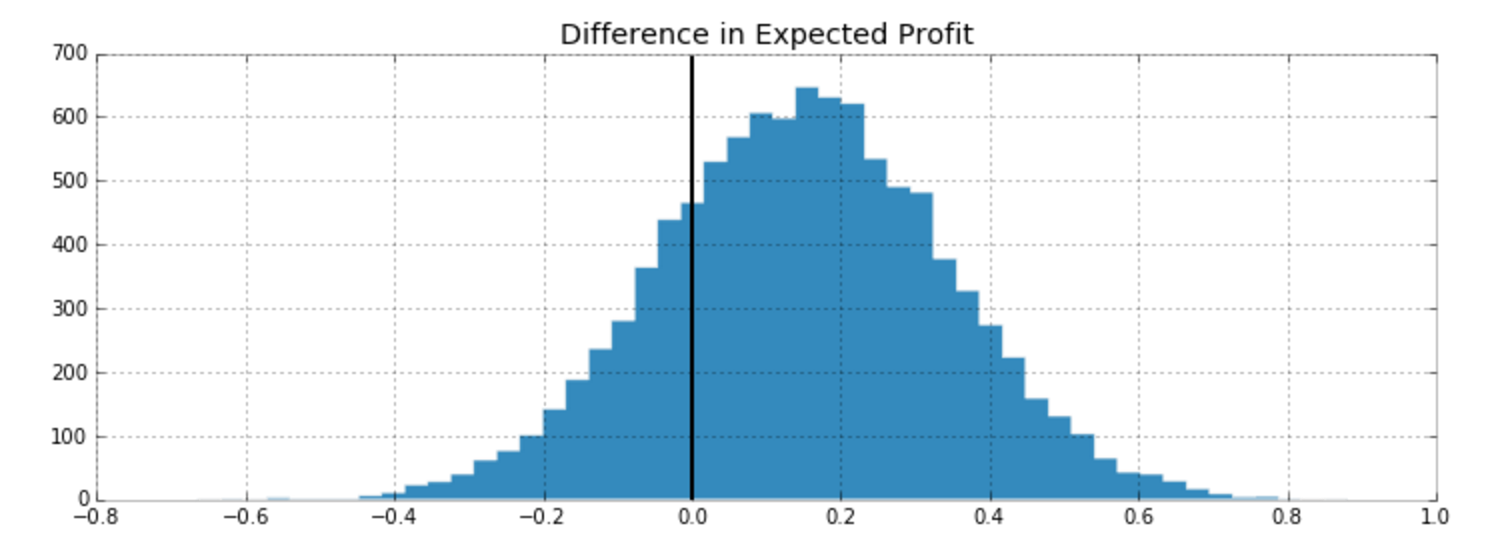
What is the probability that the Experiment group converts better than Control?
| 0.041 | < | 0.072 | == | 1 |
| 0.054 | < | 0.076 | == | 1 |
| 0.046 | < | 0.090 | == | 1 |
| 0.060 | < | 0.058 | == | 0 |
| 0.052 | < | 0.075 | == | 1 |
estimate of p is 4/5 = 0.8
99.92%
P(C_{\text{Exp}} > C_{\text{Con}} \;|\; \text{Data})
\delta = C_{\text{Exp}} - C_{\text{Con}}
\text{profit of Exp} = 22\cdot C_{\text{Exp}}
\text{profit of Con} = 30\cdot C_{\text{Con}}
\text{difference} = 22\cdot C_{\text{Exp}} - 30\cdot C_{\text{Con}}
Questions?
Does Bayesian inference replace Frequentist inference?
- No, both have preferable use cases
- Bayesian is preferable for small data or complex models
- Frequentist is preferable for large data
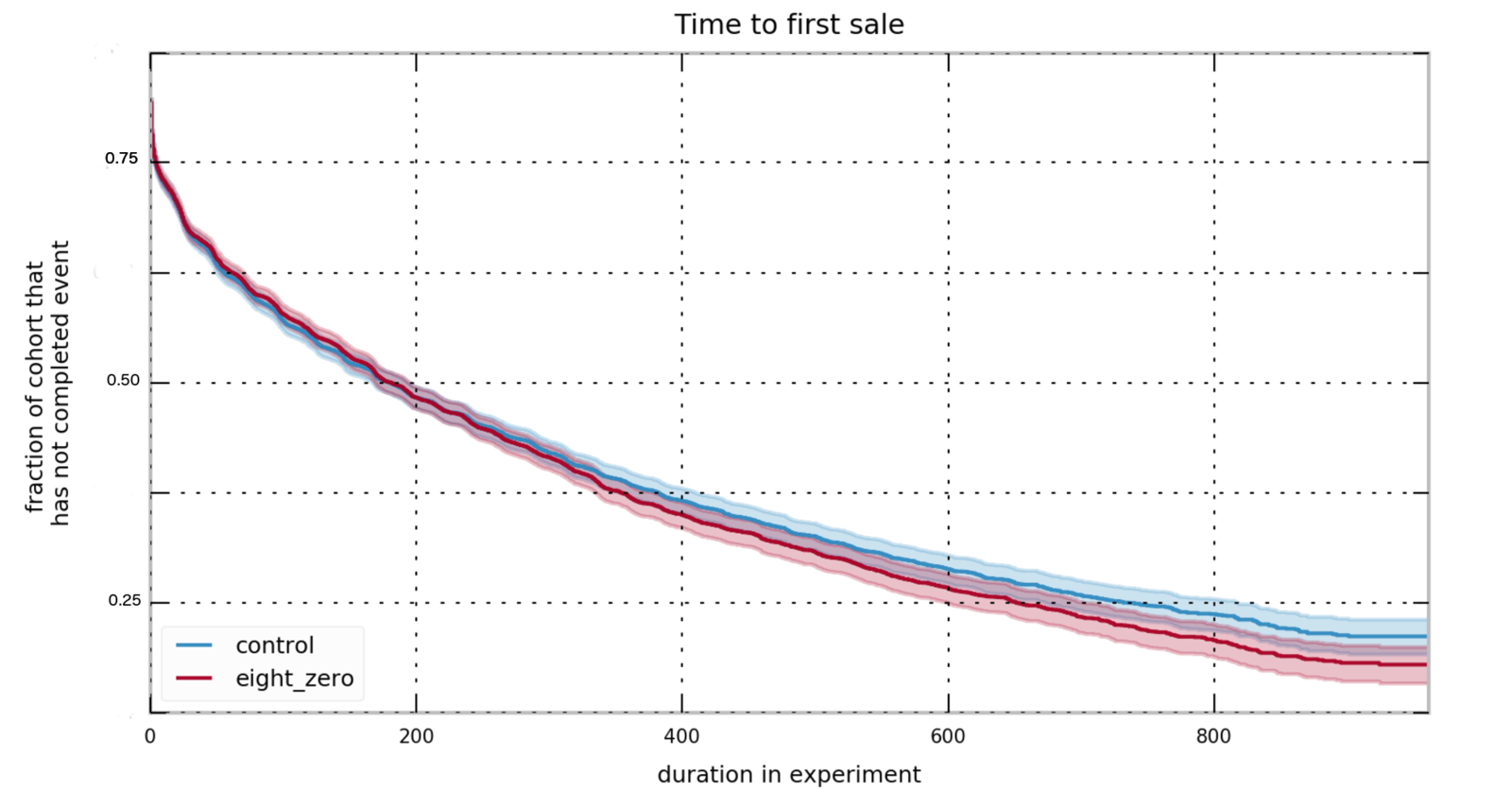
Survival Analysis in A/B testing
What are some downsides of Bayesian analysis over other methods?
- Can be computationally slow.
- Very often there is not a simple equation or formula
- Doesn't scale to big data well
What is MCMC?
- Start at current position
- Propose moving to a new position (investigate pebble near you)
- Accept/Reject the new position based on the position's adherence to the data and prior distributions (ask if the pebble came from the mountain)
- 1. If you accept, move the to new position. Save pebble.
2. Else: do not move to new position. - Return to step 1
Pseudo-algorithm
Why did I choose the exponential prior?
Does our inference depend on choice of prior?
Intro to Bayesian Inference
By Cam DP
