slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{cells counted})/ ( \text{squares counted}) \cdot \\\\ \;\;\;\;\;\;\; (\text{dilution factor}) / 0.0001 \text{mL}
slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{95})/ ( \text{5}) \cdot \\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (\text{1000}) / 0.0001 \text{mL}
slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{95})/ ( \text{5}) \cdot \\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (\text{1000}) / 0.0001 \text{mL} \\ = 4.75B \;\text{cells} / \text{mL}
slides available at bit.ly/pymcon-cell-counting

slides available at bit.ly/pymcon-cell-counting

slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{cells counted})/ ( \text{squares counted}) \cdot \\\\ \;\;\;\;\;\;\; (\text{\color{red}dilution factor}) / 0.0001 \text{mL}
slides available at bit.ly/pymcon-cell-counting
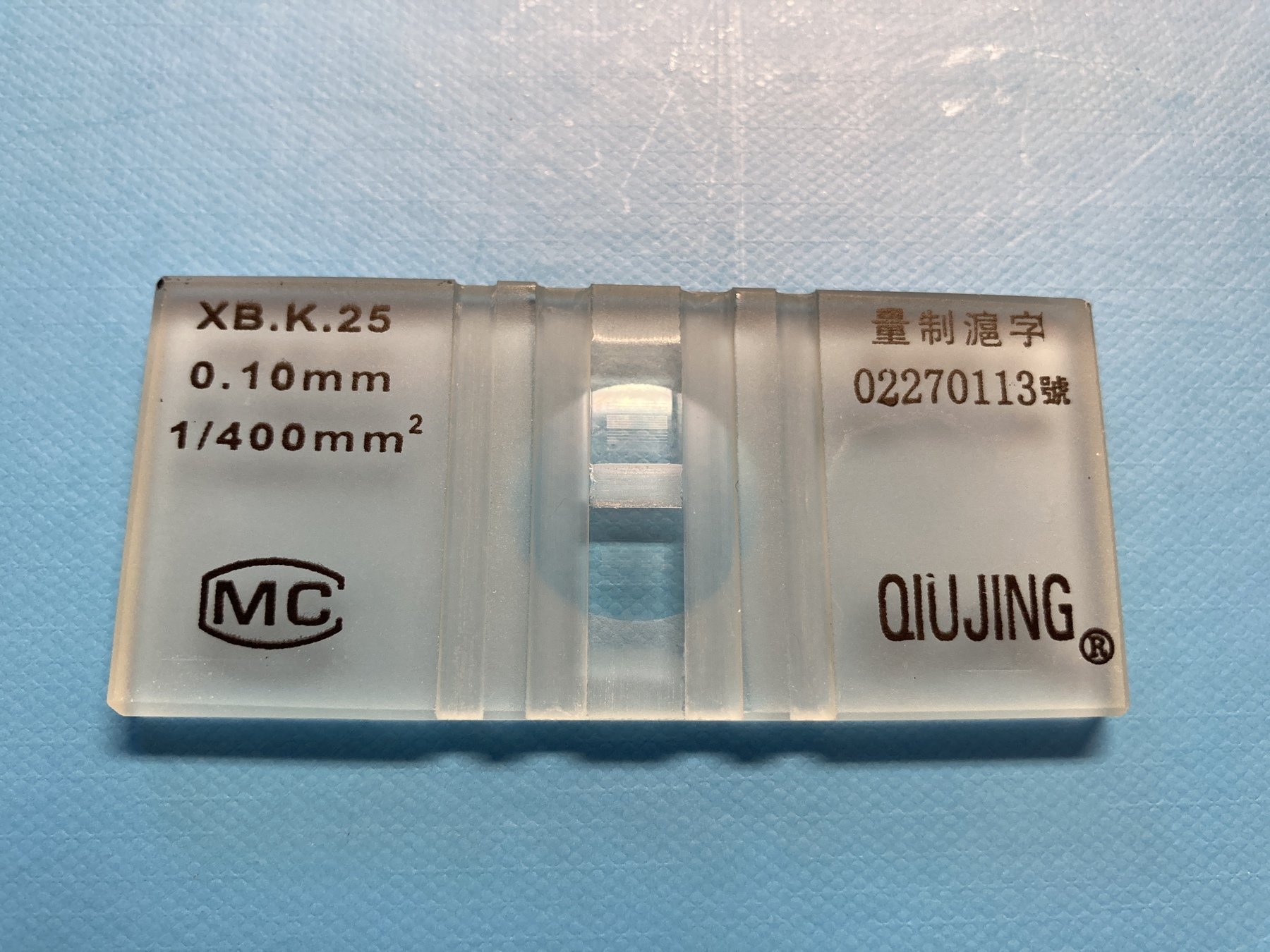
slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{cells counted})/ ( \text{squares counted}) \cdot \\\\ \;\;\;\;\;\;\; (\text{\color{red}dilution factor}) / \color{red}{0.0001} \text{mL}


slides available at bit.ly/pymcon-cell-counting
\text{cells/mL} = (\text{\color{red} cells counted})/ ( \text{squares counted}) \cdot \\\\ \;\;\;\;\;\;\; (\text{\color{red}dilution factor}) / \color{red}{0.0001} \text{mL}
import pymc3 as pm
BILLION = 1e9
TOTAL_SQUARES = 25
squares_counted = 5
yeast_counted = 95
yeast_conc = pm.Normal("cells/mL", mu=2 * BILLION, sd=0.4 * BILLION)
yeast_slurry_volume = pm.Normal("initial yeast slurry volume (mL)",
mu=1.0,
sd=0.01)
shaker1_volume = pm.Normal("shaker1 volume (mL)",
mu=9.0,
sd=0.05)
dilution_shaker1 = (yeast_slurry_volume /
(yeast_slurry_volume + shaker1_volume))
shaker2_volume = pm.Normal("shaker2 volume (mL)",
mu=9.0,
sd=0.05)
shaker1_to_shaker2_volume = pm.Normal("shaker1 to shaker2 (mL)",
mu=1.0,
sd=0.01)
dilution_shaker2 = (shaker1_to_shaker2_volume /
(shaker1_to_shaker2_volume + shaker2_volume))
shaker3_volume = pm.Normal("shaker3 volume (mL)",
mu=9.0,
sd=0.05)
shaker2_to_shaker3_volume = pm.Normal("shaker2 to shaker3 (mL)",
mu=1.0,
sd=0.01)
dilution_shaker3 = (shaker2_to_shaker3_volume /
(shaker2_to_shaker3_volume + shaker3_volume))
...
dilution_shaker1 = (yeast_slurry_volume /
(yeast_slurry_volume + shaker1_volume))
...
dilution_shaker2 = (shaker1_to_shaker2_volume /
(shaker1_to_shaker2_volume + shaker2_volume))
...
dilution_shaker3 = (shaker2_to_shaker3_volume /
(shaker2_to_shaker3_volume + shaker3_volume))
...
final_dilution_factor = dilution_shaker1 * dilution_shaker2 * dilution_shaker3
volume_of_chamber = pm.Gamma("volume of chamber (mL)", mu=0.0001, sd=0.0001 / 20)


\text{N yeast} = \text{yeast conc} \cdot \text{final dilution factor} \cdot \text{shaker3 volume}












\text{prob removed} = \text{volume of chamber} / \text{ shaker3 volume}



\text{prob removed} << 1
\text{N yeast} >> 0



\text{prob removed} << 1
\text{N yeast} >> 0
Poisson Approximation
...
final_dilution_factor = dilution_shaker1 * dilution_shaker2 * dilution_shaker3
volume_of_chamber = pm.Gamma("volume of chamber (mL)", mu=0.0001, sd=0.0001 / 20)
yeast_visible = pm.Poisson("cells in visible portion",
mu=yeast_conc * final_dilution_factor * volume_of_chamber)


import pymc3 as pm
BILLION = 1e9
TOTAL_SQUARES = 25
squares_counted = 5
yeast_counted = 95
...
yeast_visible = pm.Poisson("cells in visible portion",
mu=yeast_conc * final_dilution_factor * volume_of_chamber)
number_of_counted_cells = pm.Binomial("number of counted cells",
yeast_visible, squares_counted/TOTAL_SQUARES,
observed=yeast_counted)
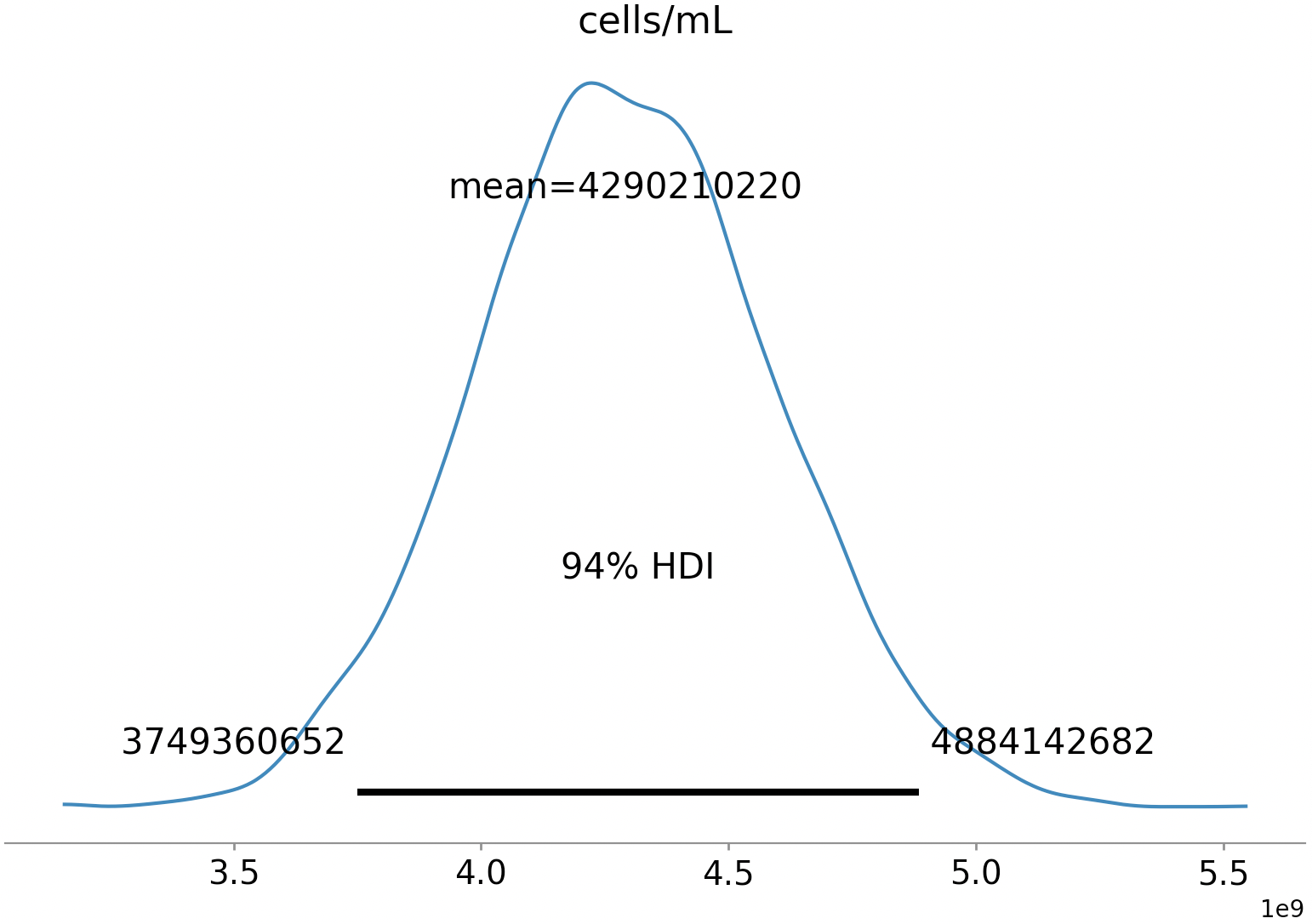



Measuring cell density in a noisy environment
By Cam DP
Measuring cell density in a noisy environment
- 274



